Topic find perimeter from area: Discover how to find the perimeter from the area with our comprehensive guide. This article covers various shapes and provides easy-to-follow methods, practical examples, and helpful tips to ensure you can calculate the perimeter accurately. Whether you're a student or a DIY enthusiast, these techniques will simplify your calculations and enhance your understanding.
Table of Content
- Finding the Perimeter from the Area
- Introduction
- Understanding Perimeter and Area
- Basic Formulas for Perimeter and Area
- Perimeter and Area of Common Shapes
- Finding Perimeter from Area: General Approach
- Square: Perimeter from Area
- Rectangle: Perimeter from Area
- Circle: Perimeter from Area
- Triangle: Perimeter from Area
- Regular Polygons: Perimeter from Area
- Using Algebra to Find Perimeter from Area
- Practical Examples and Applications
- Common Mistakes to Avoid
- Advanced Techniques and Tips
- Tools and Resources
- Conclusion
- YOUTUBE:
Finding the Perimeter from the Area
Determining the perimeter of a shape when you only know its area can be a bit challenging, as the perimeter depends on the specific dimensions of the shape. However, for some regular shapes, there are formulas that relate the area to the perimeter. Below are methods for finding the perimeter for various common shapes given their area:
Square
If you know the area (\(A\)) of a square, you can find the perimeter (\(P\)) using the following steps:
- Calculate the side length (\(s\)) of the square: \( s = \sqrt{A} \)
- Calculate the perimeter: \( P = 4s \)
Formula:
\[
P = 4 \sqrt{A}
\]
Rectangle
For a rectangle, additional information is required, such as the aspect ratio or one side length. However, if you know one side (\(l\)) and the area (\(A\)), you can find the perimeter (\(P\)):
- Calculate the other side length (\(w\)): \( w = \frac{A}{l} \)
- Calculate the perimeter: \( P = 2(l + w) \)
Formula:
\[
P = 2 \left(l + \frac{A}{l}\right)
\]
Circle
If you know the area (\(A\)) of a circle, you can find the perimeter (circumference \(C\)) using the following steps:
- Calculate the radius (\(r\)): \( r = \sqrt{\frac{A}{\pi}} \)
- Calculate the circumference: \( C = 2 \pi r \)
Formula:
\[
C = 2 \pi \sqrt{\frac{A}{\pi}}
\]
Equilateral Triangle
If you know the area (\(A\)) of an equilateral triangle, you can find the perimeter (\(P\)) using the following steps:
- Calculate the side length (\(s\)): \( s = \sqrt{\frac{4A}{\sqrt{3}}} \)
- Calculate the perimeter: \( P = 3s \)
Formula:
\[
P = 3 \sqrt{\frac{4A}{\sqrt{3}}}
\]
Summary
These formulas allow you to determine the perimeter of common shapes given their area. It is important to remember that the specific relationship between area and perimeter can vary depending on the shape and its dimensions.
Introduction
Understanding the relationship between perimeter and area is fundamental in geometry. Perimeter refers to the total length around a shape, while area measures the space within the shape. Often, knowing one can help deduce the other, especially for common geometric figures such as squares, rectangles, circles, and triangles.
In this guide, we will explore how to find the perimeter from a given area for various shapes. This process involves using basic geometric formulas and algebraic manipulation. By mastering these techniques, you can solve a variety of practical problems, from calculating the fencing needed for a garden to determining the amount of material required for construction projects.
Here's a brief overview of what we'll cover:
- Basic definitions and formulas for perimeter and area.
- Methods to derive the perimeter from the area for squares, rectangles, circles, and triangles.
- Using algebra to solve for perimeter given the area.
- Practical examples and common mistakes to avoid.
- Advanced techniques and useful tools for complex shapes.
Let's begin by reviewing the fundamental concepts of perimeter and area.
Understanding Perimeter and Area
Perimeter and area are fundamental concepts in geometry that describe different properties of shapes.
What is Perimeter?
The perimeter of a shape is the total length of its boundaries. It is the distance you would travel if you walked around the shape once. For different shapes, the perimeter can be calculated using specific formulas:
- Square: \( P = 4a \) where \( a \) is the length of a side.
- Rectangle: \( P = 2a + 2b \) where \( a \) and \( b \) are the lengths of the sides.
- Triangle: \( P = a + b + c \) where \( a \), \( b \), and \( c \) are the lengths of the sides.
- Circle: \( C = 2\pi r \) where \( r \) is the radius (the perimeter of a circle is also known as the circumference).
What is Area?
The area of a shape measures the surface it covers. It is expressed in square units (e.g., square meters, square centimeters). Different shapes have different area formulas:
- Square: \( A = a^2 \) where \( a \) is the length of a side.
- Rectangle: \( A = ab \) where \( a \) and \( b \) are the lengths of the sides.
- Triangle: \( A = \frac{1}{2}bh \) where \( b \) is the base and \( h \) is the height.
- Circle: \( A = \pi r^2 \) where \( r \) is the radius.
Key Differences Between Perimeter and Area
- Definition: Perimeter is the distance around a shape, while area is the space enclosed within it.
- Units: Perimeter is measured in linear units (e.g., meters, feet), whereas area is measured in square units (e.g., square meters, square feet).
- Calculation: The formulas for perimeter and area are different for each shape.
Why Understanding Perimeter and Area is Important
Grasping these concepts is crucial for solving various real-world problems, such as determining the amount of material needed for construction, the length of fencing required for a garden, or the size of a room.
Basic Formulas for Perimeter and Area
Understanding the basic formulas for perimeter and area is essential for solving various geometric problems. Below, we provide the formulas for common shapes:
Square
- Perimeter: \( P = 4a \) (where \( a \) is the length of a side)
- Area: \( A = a^2 \)
Rectangle
- Perimeter: \( P = 2(l + w) \) (where \( l \) is the length and \( w \) is the width)
- Area: \( A = l \times w \)
Circle
- Perimeter (Circumference): \( C = 2\pi r \) (where \( r \) is the radius)
- Area: \( A = \pi r^2 \)
Triangle
- Perimeter: \( P = a + b + c \) (where \( a \), \( b \), and \( c \) are the lengths of the sides)
- Area: \( A = \frac{1}{2} \times \text{base} \times \text{height} \)
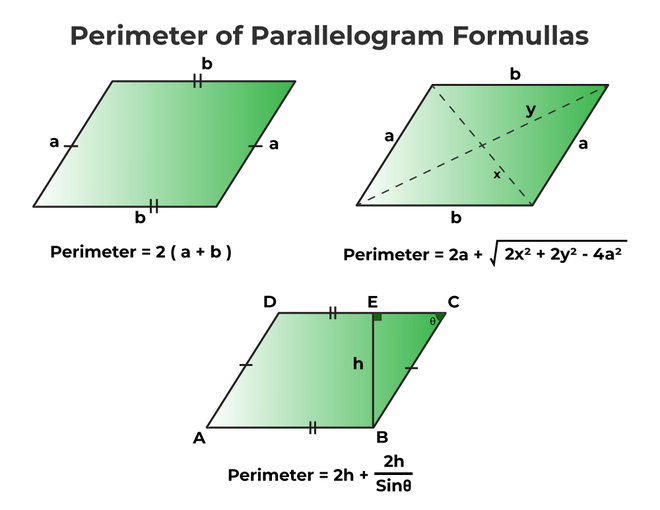
Parallelogram
- Perimeter: \( P = 2(a + b) \) (where \( a \) and \( b \) are the lengths of adjacent sides)
- Area: \( A = \text{base} \times \text{height} \)
Trapezoid (Trapezium)
- Perimeter: Sum of all sides \( P = a + b + c + d \) (for a trapezoid with sides \( a \), \( b \), \( c \), and \( d \))
- Area: \( A = \frac{1}{2} (a + b) \times h \) (where \( a \) and \( b \) are the lengths of the parallel sides, and \( h \) is the height)
Ellipse
- Area: \( A = \pi a b \) (where \( a \) and \( b \) are the semi-major and semi-minor axes, respectively)
Sector
- Area: \( A = \frac{1}{2} r^2 \theta \) (where \( r \) is the radius and \( \theta \) is the angle in radians)
These formulas serve as the foundation for calculating the perimeter and area of basic shapes. Mastery of these formulas allows for more complex problem-solving in geometry and real-world applications.
Perimeter and Area of Common Shapes
Understanding the perimeter and area of common shapes is fundamental in geometry. Below are the formulas for calculating the perimeter and area of some frequently encountered shapes:
Square
- Perimeter: \( P = 4s \)
- Area: \( A = s^2 \)
Rectangle
- Perimeter: \( P = 2l + 2w \)
- Area: \( A = lw \)
Triangle
- Perimeter: \( P = a + b + c \)
- Area: \( A = \frac{1}{2}bh \)
Circle
- Circumference (Perimeter): \( C = 2\pi r \) or \( C = \pi d \)
- Area: \( A = \pi r^2 \)
Parallelogram
- Perimeter: \( P = 2(a + b) \)
- Area: \( A = bh \)
Trapezoid
- Perimeter: \( P = a + b_1 + c + b_2 \)
- Area: \( A = \frac{1}{2}h(b_1 + b_2) \)
These formulas are essential for solving various geometric problems and are commonly used in different fields such as architecture, engineering, and everyday measurements.

Finding Perimeter from Area: General Approach
Finding the perimeter of a shape given its area can be a challenging but insightful mathematical problem. The approach varies depending on the type of shape and its properties. Here is a general approach to tackle this problem:
-
Identify the Shape:
Determine the type of shape (e.g., square, rectangle, circle, triangle) for which you have the area. Different shapes have different relationships between their area and perimeter.
-
Use Known Formulas:
-
Square:
For a square, if the area \( A \) is known, the side length \( s \) can be found using the formula:
\[ s = \sqrt{A} \]
Then, the perimeter \( P \) is:
\[ P = 4s \]
-
Rectangle:
For a rectangle with length \( l \) and width \( w \), if the area \( A \) is given:
\[ A = l \times w \]
and the perimeter \( P \) is:
\[ P = 2(l + w) \]
Additional information or assumptions (such as the aspect ratio) might be needed to find \( l \) and \( w \) from \( A \).
-
Circle:
For a circle, if the area \( A \) is given, the radius \( r \) can be calculated using:
\[ r = \sqrt{\frac{A}{\pi}} \]
The perimeter (circumference) \( C \) is:
\[ C = 2\pi r \]
-
Triangle:
For triangles, the process can be more complex. If it is an equilateral triangle with area \( A \), the side length \( s \) can be found using:
\[ s = \sqrt{\frac{4A}{\sqrt{3}}} \]
Then, the perimeter \( P \) is:
\[ P = 3s \]
For other types of triangles, additional information (such as the length of one side or the height) is usually required.
-
-
Algebraic Manipulation:
If the shape is more complex or not standard, use algebraic manipulation to express the perimeter in terms of the area. This often involves setting up equations based on the known properties of the shape and solving for the desired dimensions.
-
Verification:
Once you have calculated the perimeter, verify your results by checking if they are consistent with the given area and the properties of the shape.
This approach provides a structured way to find the perimeter from the area of various shapes, ensuring accuracy and a clear understanding of the mathematical relationships involved.
Square: Perimeter from Area
To find the perimeter of a square when the area is given, follow these steps:
- Start with the formula for the area of a square:
\( A = a^2 \)
where \( A \) is the area and \( a \) is the length of one side.
- Solve for the side length:
\( a = \sqrt{A} \)
- Use the side length to find the perimeter:
\( P = 4a \)
Here is a step-by-step example:
- Given: The area of the square is \( 64 \, \text{cm}^2 \).
- Find the side length:
\( a = \sqrt{64} = 8 \, \text{cm} \)
- Calculate the perimeter:
\( P = 4 \times 8 = 32 \, \text{cm} \)
Thus, the perimeter of a square with an area of \( 64 \, \text{cm}^2 \) is \( 32 \, \text{cm} \).
Here’s a summary in a table format:
| Step | Calculation | Result |
|---|---|---|
| 1. Find the side length from area | \( a = \sqrt{A} \) | \( a = \sqrt{64} = 8 \, \text{cm} \) |
| 2. Calculate the perimeter | \( P = 4a \) | \( P = 4 \times 8 = 32 \, \text{cm} \) |
Rectangle: Perimeter from Area
To find the perimeter of a rectangle when the area is known, we need to use the relationship between the area, length, and width of the rectangle.
The formulas involved are:
- Area of a rectangle: \( A = l \times w \)
- Perimeter of a rectangle: \( P = 2(l + w) \)
Here are the steps to find the perimeter from the area:
- Determine one side (length or width):
To find the perimeter, you need to know either the length (\( l \)) or the width (\( w \)) of the rectangle. If only the area is given, you might need additional information about either the length or the width. Let's assume you know the length (\( l \)).
- Calculate the missing dimension:
Use the area formula to find the width:
\[
w = \frac{A}{l}
\]Where \( A \) is the area, and \( l \) is the known length.
- Calculate the perimeter:
Once you have both the length and the width, use the perimeter formula:
\[
P = 2(l + w)
\]Substitute the values of \( l \) and \( w \) into this formula to get the perimeter.
Let's consider an example:
| Given: | Area (\( A \)) = 50 square units, Length (\( l \)) = 10 units |
| Find: | Width (\( w \)) |
Step 1: Calculate the width:
\[
w = \frac{A}{l} = \frac{50}{10} = 5 \text{ units}
\]
Step 2: Calculate the perimeter:
\[
P = 2(l + w) = 2(10 + 5) = 2 \times 15 = 30 \text{ units}
\]
Therefore, the perimeter of the rectangle is 30 units.
This approach can be generalized for any rectangle where the area and one dimension are known. If neither dimension is known, you will need additional information to find the perimeter.
Circle: Perimeter from Area
To find the perimeter (circumference) of a circle when the area is given, follow these steps:
-
Recall the formula for the area of a circle:
\( A = \pi r^2 \)
-
Solve for the radius:
Rearrange the area formula to solve for the radius \( r \):
\( r = \sqrt{\frac{A}{\pi}} \)
-
Recall the formula for the circumference:
\( C = 2\pi r \)
-
Substitute the radius into the circumference formula:
\( C = 2\pi \sqrt{\frac{A}{\pi}} \)
-
Simplify the expression:
\( C = 2 \sqrt{\pi A} \)
Let's go through an example:
-
Given: The area of a circle is 50 square centimeters.
-
Calculate the radius:
\( r = \sqrt{\frac{50}{\pi}} \approx \sqrt{\frac{50}{3.14}} \approx 3.99 \, \text{cm} \)
-
Calculate the circumference:
\( C = 2\pi \times 3.99 \approx 2 \times 3.14 \times 3.99 \approx 25.07 \, \text{cm} \)
Thus, the perimeter (circumference) of the circle is approximately 25.07 centimeters.
This method provides a systematic approach to find the perimeter of a circle from its area, ensuring accurate and efficient calculations.

Triangle: Perimeter from Area
Finding the perimeter of a triangle when you know the area can be more complex compared to squares or rectangles, as it depends on the type of triangle and the given information. Below are the steps and formulas for finding the perimeter of different types of triangles based on the area.
Equilateral Triangle
For an equilateral triangle, where all sides are equal, the process is straightforward:
- Given the area \( A \) of an equilateral triangle, use the formula for the area: \[ A = \frac{\sqrt{3}}{4} s^2 \] where \( s \) is the length of a side.
- Solve for \( s \): \[ s = \sqrt{\frac{4A}{\sqrt{3}}} \]
- Find the perimeter \( P \) by multiplying the side length by 3: \[ P = 3s \]
Isosceles Triangle
For an isosceles triangle, where two sides are equal, follow these steps:
- Given the area \( A \) and the base \( b \), use the formula for the area: \[ A = \frac{b}{4} \sqrt{4a^2 - b^2} \] where \( a \) is the length of the equal sides.
- Solve for \( a \): \[ a = \sqrt{\left(\frac{4A}{b}\right)^2 + \left(\frac{b}{2}\right)^2} \]
- Find the perimeter \( P \) by adding the lengths of all sides: \[ P = 2a + b \]
Right Triangle
For a right triangle, the process involves using the Pythagorean theorem:
- Given the area \( A \) and one leg \( a \), use the area formula: \[ A = \frac{1}{2}ab \] where \( b \) is the other leg.
- Solve for \( b \): \[ b = \frac{2A}{a} \]
- Use the Pythagorean theorem to find the hypotenuse \( c \): \[ c = \sqrt{a^2 + b^2} \]
- Find the perimeter \( P \) by adding all sides: \[ P = a + b + c \]
Scalene Triangle
For a scalene triangle, where all sides are different, it can be more complicated. Here’s a general approach using Heron's formula:
- Given the area \( A \) and the lengths of the sides \( a \), \( b \), and \( c \), use Heron's formula: \[ A = \sqrt{s(s-a)(s-b)(s-c)} \] where \( s \) is the semi-perimeter: \[ s = \frac{a + b + c}{2} \]
- Solve the equation for one side if the other two sides and area are known. This step may require iterative methods or numerical solutions as it involves solving a polynomial equation.
- Once all sides are determined, sum them to find the perimeter \( P \): \[ P = a + b + c \]
Using Algebra to Simplify Calculations
In some cases, using algebraic methods or numerical algorithms can simplify the process of finding the perimeter from the area, especially for scalene triangles. Techniques like solving quadratic equations or using trigonometric identities may be useful.
In summary, the approach to finding the perimeter from the area of a triangle varies based on the type of triangle and the given information. Understanding and applying the right formulas and steps is key to solving these problems.
Regular Polygons: Perimeter from Area
Finding the perimeter of a regular polygon (where all sides and angles are equal) from its area involves using specific geometric properties and formulas. Here is a step-by-step guide:
General Approach
For a regular polygon with \( n \) sides, each of length \( s \), the perimeter \( P \) can be found from the given area \( A \) using the following steps:
- Determine the formula for the area of a regular polygon: \[ A = \frac{1}{4} n s^2 \cot\left(\frac{\pi}{n}\right) \]
- Solve for the side length \( s \): \[ s = \sqrt{\frac{4A}{n \cot\left(\frac{\pi}{n}\right)}} \]
- Calculate the perimeter \( P \): \[ P = n \cdot s \]
Example: Regular Hexagon
For a regular hexagon, where \( n = 6 \):
- Given the area \( A \), use the formula: \[ A = \frac{3 \sqrt{3}}{2} s^2 \]
- Solve for \( s \): \[ s = \sqrt{\frac{2A}{3 \sqrt{3}}} \]
- Calculate the perimeter \( P \): \[ P = 6 \cdot s \]
Example: Regular Pentagon
For a regular pentagon, where \( n = 5 \):
- Given the area \( A \), use the formula: \[ A = \frac{1}{4} \sqrt{5(5+2\sqrt{5})} s^2 \]
- Solve for \( s \): \[ s = \sqrt{\frac{4A}{\sqrt{5(5+2\sqrt{5})}}} \]
- Calculate the perimeter \( P \): \[ P = 5 \cdot s \]
Example: Regular Octagon
For a regular octagon, where \( n = 8 \):
- Given the area \( A \), use the formula: \[ A = 2 (1 + \sqrt{2}) s^2 \]
- Solve for \( s \): \[ s = \sqrt{\frac{A}{2(1 + \sqrt{2})}} \]
- Calculate the perimeter \( P \): \[ P = 8 \cdot s \]
Using Algebra and Trigonometry
For any regular polygon, algebraic manipulation and trigonometric identities can simplify finding the perimeter. The use of the cotangent function \( \cot \left( \frac{\pi}{n} \right) \) is particularly useful in generalizing the formula for the area and perimeter.
In summary, finding the perimeter of a regular polygon from its area involves using specific formulas for different shapes, solving for the side length, and then calculating the perimeter. This method works universally for all regular polygons by substituting the number of sides \( n \) and applying the corresponding formulas.
Using Algebra to Find Perimeter from Area
Finding the perimeter of a shape when given its area involves using algebraic methods to solve for the unknown perimeter. This section will explain how to approach this problem for different shapes using algebra.
Square
For a square, the relationship between the area (A) and the side length (s) is given by:
\( A = s^2 \)
To find the perimeter (P) from the area:
- Solve for the side length: \( s = \sqrt{A} \)
- Calculate the perimeter: \( P = 4s \)
For example, if the area of a square is 64 square units:
- \( s = \sqrt{64} = 8 \)
- \( P = 4 \times 8 = 32 \) units
Rectangle
To find the perimeter of a rectangle from its area, you need additional information such as the length (l) or width (w). Given the area formula:
\( A = l \times w \)
If one dimension is known, the other can be found:
- Let the known dimension be l. Solve for w: \( w = \frac{A}{l} \)
- Calculate the perimeter: \( P = 2(l + w) \)
For instance, if the area is 50 square units and the length is 10 units:
- \( w = \frac{50}{10} = 5 \)
- \( P = 2(10 + 5) = 30 \) units
Circle
For a circle, the area (A) is related to the radius (r) by the formula:
\( A = \pi r^2 \)
To find the circumference (perimeter, C):
- Solve for the radius: \( r = \sqrt{\frac{A}{\pi}} \)
- Calculate the circumference: \( C = 2\pi r \)
If the area is 100π square units:
- \( r = \sqrt{\frac{100\pi}{\pi}} = 10 \)
- \( C = 2\pi \times 10 = 20\pi \) units
Triangle
For a triangle, especially equilateral, where each side is of equal length:
\( A = \frac{\sqrt{3}}{4} s^2 \)
To find the perimeter:
- Solve for the side length: \( s = \sqrt{\frac{4A}{\sqrt{3}}} \)
- Calculate the perimeter: \( P = 3s \)
If the area is 16 square units:
- \( s = \sqrt{\frac{4 \times 16}{\sqrt{3}}} = \sqrt{\frac{64}{1.732}} \approx 6.16 \)
- \( P = 3 \times 6.16 \approx 18.48 \) units
Regular Polygons
For regular polygons (polygons with all sides and angles equal), the area (A) can be found using the formula involving the side length (s) and the number of sides (n):
\( A = \frac{1}{4} n s^2 \cot(\frac{\pi}{n}) \)
To find the perimeter (P):
- Solve for the side length: \( s = \sqrt{\frac{4A}{n \cot(\frac{\pi}{n})}} \)
- Calculate the perimeter: \( P = n \times s \)
For example, for a regular hexagon (n=6) with an area of 54 square units:
- \( s = \sqrt{\frac{4 \times 54}{6 \cot(\frac{\pi}{6})}} = \sqrt{\frac{216}{6 \times \sqrt{3}/3}} = \sqrt{\frac{216}{2 \sqrt{3}}} \approx 4.68 \)
- \( P = 6 \times 4.68 \approx 28.08 \) units
Using these algebraic methods, you can determine the perimeter of various shapes from their given area, provided you have the necessary additional information or properties of the shapes.
Practical Examples and Applications
Understanding how to find the perimeter from the area has numerous practical applications in everyday life. Here are some examples and step-by-step guides on how this concept is applied:
1. Gardening
When building a fence for a garden, you need to know how much fencing material to purchase. If you know the area of the garden, you can estimate the perimeter to buy the correct amount of fencing.
- Suppose your garden area is 200 square feet, and it is rectangular with a length twice its width.
- Let the width be w, then the length is 2w.
- The area is given by w * 2w = 200, so 2w2 = 200.
- Solve for w: w = \sqrt{100} = 10 feet.
- The length is 2 * 10 = 20 feet.
- Now calculate the perimeter: 2(l + w) = 2(20 + 10) = 60 feet.
2. Building a Shed
To construct a shed, knowing the perimeter helps determine the amount of materials needed for the walls.
- Assume the shed has an area of 120 square feet and is rectangular with a width of 10 feet.
- Let the length be l, then 10 * l = 120.
- Solve for l: l = 120 / 10 = 12 feet.
- Calculate the perimeter: 2(l + w) = 2(12 + 10) = 44 feet.
3. Painting a Room
When painting a room, knowing the perimeter helps calculate the amount of paint needed for the walls.
- If a room has a floor area of 150 square feet and is rectangular with a length of 15 feet:
- Let the width be w, then 15 * w = 150.
- Solve for w: w = 150 / 15 = 10 feet.
- Calculate the perimeter: 2(l + w) = 2(15 + 10) = 50 feet.
4. Surveying Land
In property surveying, the perimeter is essential for determining boundary lengths.
- For a piece of land with an area of 500 square feet and a square shape:
- Each side length is s, and s2 = 500.
- Solve for s: s = \sqrt{500} \approx 22.36 feet.
- Calculate the perimeter: 4 * s = 4 * 22.36 \approx 89.44 feet.
These practical examples demonstrate how calculating the perimeter from the area is essential in various real-world scenarios, from gardening and construction to painting and land surveying.

Common Mistakes to Avoid
When calculating the perimeter from the area, it’s important to avoid common mistakes that can lead to incorrect results. Here are some of the most frequent errors and tips to prevent them:
- Assuming Shape:
One of the most common mistakes is assuming the shape of the figure without proper information. Different shapes require different formulas. Always confirm the shape before proceeding with calculations.
- Incorrect Formula:
Using the wrong formula for a given shape is another frequent error. Ensure that you are applying the correct formula for perimeter based on the shape's properties. For instance, using the formula for a rectangle's perimeter on a square will yield incorrect results.
- Unit Consistency:
Make sure that all measurements are in the same unit before performing calculations. Mixing units can lead to significant errors. Convert all measurements to the same unit, such as meters or feet, before using them in formulas.
- Misinterpretation of Area:
Sometimes, the area provided might be of a composite shape. Misinterpreting the area without breaking it down into simpler shapes can lead to errors. Analyze and decompose the shape if necessary.
- Algebraic Errors:
When solving for perimeter using algebra, errors in algebraic manipulation are common. Double-check each step of your calculations to ensure accuracy. For example, solving for the side of a square when given its area involves taking the square root correctly.
Example:
- Given Area \( A \) of a square: \( A = s^2 \)
- To find the side length \( s \): \( s = \sqrt{A} \)
- Then calculate the perimeter \( P \): \( P = 4s \)
- Ignoring Shape Properties:
For shapes like rectangles, circles, and triangles, understanding specific properties is crucial. For instance, for a circle, the relationship between radius, area, and circumference must be understood clearly.
Example for a circle:
- Given Area \( A \): \( A = \pi r^2 \)
- To find the radius \( r \): \( r = \sqrt{\frac{A}{\pi}} \)
- Then calculate the circumference \( C \): \( C = 2\pi r \)
- Overlooking Practical Considerations:
In real-world applications, factors such as measurement accuracy, material properties, and environmental conditions can affect calculations. Always consider these factors and allow for a margin of error where necessary.
- Not Reviewing Calculations:
Always review your calculations to catch any mistakes. Simple arithmetic errors or misreading values can lead to incorrect results. Double-checking your work helps to ensure accuracy.
Advanced Techniques and Tips
Finding the perimeter from the area can be straightforward for some shapes, but there are advanced techniques and tips that can help with more complex cases or improve accuracy. Here are some advanced methods and useful tips:
- Using Algebraic Manipulation: For shapes like rectangles, knowing one side can simplify finding the perimeter. Given the area \( A \) and one side \( a \), you can find the other side \( b \) using \( b = \frac{A}{a} \). Then, use the perimeter formula \( P = 2(a + b) \).
- Working with Circles: For circles, the perimeter (circumference) can be derived from the area \( A \). Use the formula: \[ C = 2\pi \sqrt{\frac{A}{\pi}} \] This formula combines the area and the known relationship between radius and circumference.
- Equilateral Triangles: If you know the area of an equilateral triangle, you can find the perimeter using: \[ P = 3 \times \sqrt{\frac{4A}{\sqrt{3}}} \] This formula derives from the relationship between the area and side length of an equilateral triangle.
- Scaling and Similar Shapes: For similar shapes, the perimeter scales linearly with the dimensions. If you know the scaling factor \( k \) between two similar shapes, the perimeter of the second shape \( P_2 \) can be found from the perimeter of the first shape \( P_1 \) using \( P_2 = k \times P_1 \).
- Using Software Tools: Utilize geometry software and tools that can handle complex calculations and provide visual aids. These tools can perform operations on irregular shapes and offer step-by-step solutions.
- Understanding Limitations: Recognize the limitations of your formulas. For instance, the perimeter of irregular shapes cannot be determined from the area alone without additional information about the shape's geometry.
- Applying Integral Calculus: For advanced cases, particularly irregular shapes, integral calculus can be used to find the perimeter. The perimeter can be approximated by integrating along the boundary of the shape: \[ P = \int_{0}^{L} \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2} \, dt \] where \( L \) is the length of the boundary.
- Practical Applications: When applying these techniques in real-life scenarios, consider measurement accuracy, units consistency, and material properties that might affect the perimeter measurement.
By using these advanced techniques and tips, you can accurately find the perimeter from the area for a variety of shapes, whether simple or complex.
Tools and Resources
Finding the perimeter from a given area can be a complex task that benefits greatly from the use of specialized tools and resources. Here are some of the best tools and resources available to help you calculate and understand perimeter and area relationships:
-
Khan Academy:
Khan Academy offers a comprehensive collection of tutorials, exercises, and quizzes on area and perimeter for various shapes, including triangles, rectangles, circles, and composite figures. The interactive platform helps reinforce learning through step-by-step problem-solving and immediate feedback.
-
GeoGebra:
GeoGebra provides a suite of mathematical tools that includes calculators for geometry, graphing, and 3D modeling. The GeoGebra Geometry app is particularly useful for visualizing and solving perimeter and area problems interactively.
-
PhET Interactive Simulations:
PhET offers interactive simulations that help visualize and understand the concepts of area and perimeter through engaging activities. These simulations allow for experimentation with different shapes and provide a hands-on learning experience.
-
STEM Learning Resources:
STEM Learning provides various educational materials, including practical activities, worksheets, and games focused on teaching area and perimeter. These resources are designed to enhance understanding through practice and real-world applications.
Online Calculators and Software
Here are some specific online tools that can assist in calculating perimeter from a given area:
-
Online Perimeter Calculators:
Many websites offer free calculators where you can input the area of a shape to find its perimeter. These tools often cover standard shapes like squares, rectangles, and circles.
-
Mathway:
Mathway is an online problem solver that can handle a wide range of mathematical problems, including finding perimeters from areas. It provides step-by-step solutions and explanations.
Books and Textbooks
For those who prefer traditional learning methods, there are several textbooks and books available that cover the topics of perimeter and area in detail:
-
"Geometry for Dummies":
This book offers a comprehensive guide to understanding geometry concepts, including detailed sections on calculating area and perimeter for various shapes.
-
"Mathematics for the International Student":
These series of textbooks are designed for high school students and cover a wide range of mathematical concepts, including perimeter and area, with practice problems and solutions.
Mobile Apps
There are several mobile apps available for learning and calculating perimeter and area:
-
Photomath:
This app allows users to take pictures of math problems and provides instant solutions and explanations, making it useful for finding perimeters from given areas.
-
Geometry Pad:
Geometry Pad is an interactive geometry app that helps users draw and manipulate shapes to explore their properties, including perimeter and area calculations.
Conclusion
Understanding how to find the perimeter from the area is a fundamental concept in geometry that applies to a wide range of shapes and real-world scenarios. By mastering the relationship between these two properties, you can enhance your problem-solving skills and apply them to various mathematical and practical situations.
Throughout this guide, we have explored various shapes including squares, rectangles, circles, triangles, and regular polygons. We have also delved into more advanced techniques and provided practical examples to solidify your understanding. Here are the key takeaways:
- For regular shapes like squares and circles, the formulas to find the perimeter from the area are straightforward and involve basic algebraic manipulation.
- For rectangles and triangles, the process involves using additional information such as the length of one side or the height to derive the perimeter from the given area.
- Advanced techniques involve using algebraic equations and calculus for more complex shapes and scenarios.
- Tools and resources such as online calculators, geometry software, and educational websites can greatly aid in these calculations.
In conclusion, the ability to find the perimeter from the area is an essential skill that can be applied in various fields such as architecture, engineering, and everyday problem-solving. By using the techniques and resources discussed, you can approach these problems with confidence and accuracy. Keep practicing and exploring different shapes and scenarios to deepen your understanding and proficiency in this area of mathematics.

Tìm Chu Vi và Diện Tích của Hình Hợp | Ví Dụ Hình Chữ L | Hình Học | Toán Học với Thầy J
Video hướng dẫn cách tìm chu vi của hình vuông khi biết diện tích. Học cách tính toán dễ dàng và nhanh chóng.
Cách tìm chu vi hình vuông nếu biết diện tích