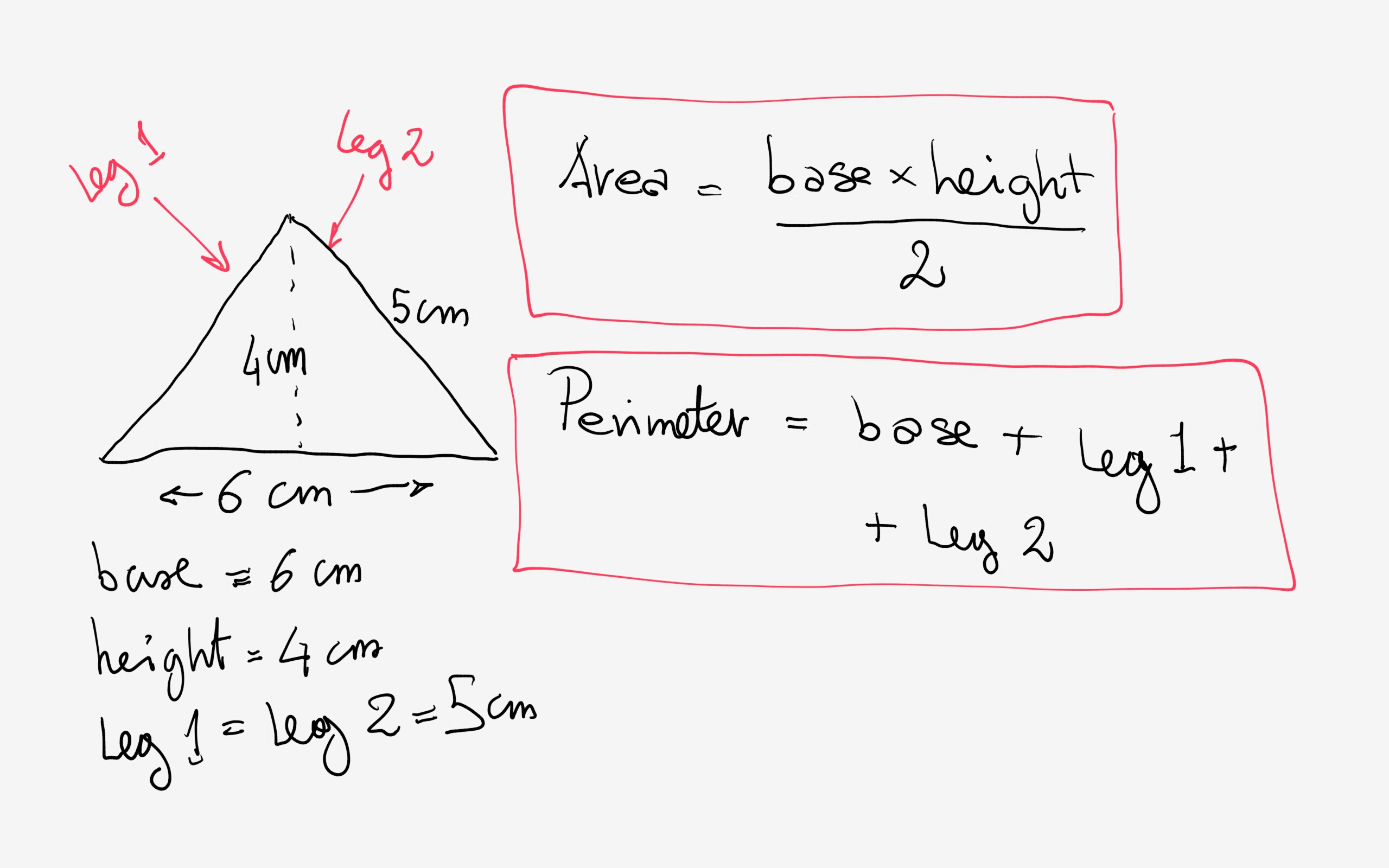
Topic finding the area and perimeter of a triangle: Finding the area and perimeter of a triangle is essential for many practical applications in geometry. This article will guide you through simple and effective methods to calculate these important properties, ensuring you can confidently solve any triangle-related problem you encounter. Whether for school, work, or personal projects, understanding these calculations is invaluable.
Table of Content
- Finding the Area and Perimeter of a Triangle
- Introduction
- Basic Definitions
- Formulas for Area
- Formulas for Perimeter
- Step-by-Step Examples
- Applications and Real-life Examples
- Practice Problems
- Frequently Asked Questions
- YOUTUBE: Video hướng dẫn cách tìm diện tích và chu vi của tam giác một cách dễ hiểu và chi tiết. Phù hợp cho học sinh và giáo viên.
Finding the Area and Perimeter of a Triangle
Understanding the formulas and methods to calculate the area and perimeter of a triangle is fundamental in geometry. Below, you will find the necessary formulas and examples for different types of triangles.
Area of a Triangle
The area of a triangle can be calculated using various formulas depending on the known dimensions:
- Base and Height: The most common formula is: \[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \]
- Heron's Formula: When the lengths of all three sides are known: \[ s = \frac{a + b + c}{2} \] \[ \text{Area} = \sqrt{s(s - a)(s - b)(s - c)} \] where \( a \), \( b \), and \( c \) are the lengths of the sides, and \( s \) is the semi-perimeter.
- Two Sides and Included Angle: When two sides and the included angle are known: \[ \text{Area} = \frac{1}{2} \times a \times b \times \sin(\theta) \] where \( \theta \) is the angle between sides \( a \) and \( b \).
Examples
Find the area of a triangle with a base of 10 inches and a height of 5 inches.
\[ \text{Area} = \frac{1}{2} \times 10 \times 5 = 25 \text{ in}^2 \]Find the area of an equilateral triangle with a side length of 2 cm.
\[ \text{Area} = \frac{\sqrt{3}}{4} \times 2^2 = 1.73 \text{ cm}^2 \]
Perimeter of a Triangle
The perimeter of a triangle is the total distance around the triangle. The formula varies based on the type of triangle:
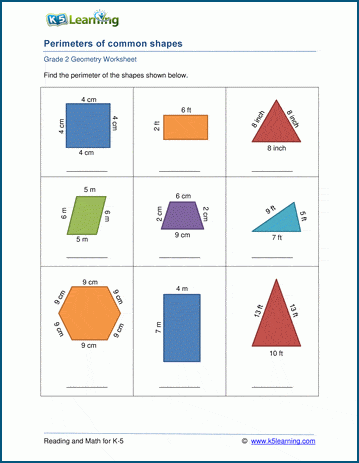
- General Formula: For any triangle with sides \( a \), \( b \), and \( c \): \[ \text{Perimeter} = a + b + c \]
- Example: Find the perimeter of a triangle with sides 3 cm, 4 cm, and 5 cm. \[ \text{Perimeter} = 3 + 4 + 5 = 12 \text{ cm} \]
Special Triangles
Equilateral Triangle
- Area: \[ \text{Area} = \frac{\sqrt{3}}{4} \times \text{side}^2 \]
- Perimeter: \[ \text{Perimeter} = 3 \times \text{side} \]
Right-Angled Triangle
- Area: \[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \]
- Perimeter: Sum of the three sides.
Isosceles Triangle
- Area: \[ \text{Area} = \frac{1}{4} \times b \times \sqrt{4a^2 - b^2} \] where \( a \) is the length of the equal sides, and \( b \) is the base.
Practice Questions
- Calculate the area of a triangle with a base of 6 cm and a height of 8 cm.
- Find the perimeter of an equilateral triangle with each side measuring 5 cm.
- Use Heron's formula to find the area of a triangle with sides 7 cm, 8 cm, and 9 cm.

READ MORE:
Introduction
Finding the area and perimeter of a triangle is a fundamental concept in geometry that is applicable in various fields such as architecture, engineering, and even art. Understanding these measurements helps in determining the size of a triangular space and the boundary length around it. This section will guide you through different methods and formulas to calculate the area and perimeter of various types of triangles including right-angled, equilateral, and isosceles triangles.
- The area of a triangle is the total region enclosed by its three sides. It is generally calculated using the formula: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \).
- The perimeter of a triangle is the total length of its boundary, which is the sum of the lengths of its three sides: \( \text{Perimeter} = a + b + c \).
- For equilateral triangles, where all sides are equal, the area can also be calculated using the formula: \( \text{Area} = \frac{\sqrt{3}}{4} \times \text{side}^2 \).
- Heron's formula is used to find the area when all three sides of the triangle are known: \[ s = \frac{a + b + c}{2} \] \[ \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} \]
- For right-angled triangles, the area can be directly found by considering one leg as the base and the other leg as the height: \( \text{Area} = \frac{1}{2} \times \text{leg}_1 \times \text{leg}_2 \).
These formulas and methods provide a comprehensive approach to accurately determining the area and perimeter of any triangle. By mastering these calculations, you can apply them to real-world scenarios such as land measurement, construction, and various design projects.
Basic Definitions
In this section, we will cover the basic definitions related to finding the area and perimeter of a triangle.
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. The area and perimeter are fundamental properties that can be calculated using specific formulas.
- Perimeter of a Triangle: The perimeter is the total length of all three sides of a triangle. If a triangle has sides \(a\), \(b\), and \(c\), the perimeter \(P\) is given by: \[ P = a + b + c \]
- Area of a Triangle: The area of a triangle is the amount of space enclosed by the triangle. For a triangle with base \(b\) and height \(h\), the area \(A\) is calculated using: \[ A = \frac{1}{2} \times b \times h \] where the height is the perpendicular distance from the base to the opposite vertex.
- Equilateral Triangle: A triangle with all three sides of equal length. The area of an equilateral triangle with side length \(a\) is: \[ A = \frac{\sqrt{3}}{4} a^2 \]
- Isosceles Triangle: A triangle with at least two sides of equal length. The area can be found if the base \(b\) and the length of the equal sides \(a\) are known: \[ A = \frac{1}{4} b \sqrt{4a^2 - b^2} \]
- Scalene Triangle: A triangle with all sides of different lengths. The area can be determined using Heron's formula if all three side lengths are known. For a triangle with sides \(a\), \(b\), and \(c\), and semi-perimeter \(s = \frac{a + b + c}{2}\): \[ A = \sqrt{s(s - a)(s - b)(s - c)} \]
- Right-Angled Triangle: A triangle with one angle equal to 90 degrees. The area for a right-angled triangle with legs \(a\) and \(b\) is: \[ A = \frac{1}{2} \times a \times b \]
Understanding these basic definitions and formulas is essential for calculating the area and perimeter of various types of triangles accurately.
Formulas for Area
The area of a triangle can be calculated using different formulas depending on the type of triangle and the known measurements. Here are some common methods:
- Base and Height Method: The most common formula for finding the area of a triangle is: \[ A = \frac{1}{2} \times b \times h \] where \( A \) is the area, \( b \) is the base, and \( h \) is the height of the triangle.
- Heron's Formula: When the lengths of all three sides are known, Heron's formula can be used: \[ A = \sqrt{s(s-a)(s-b)(s-c)} \] where \( s \) is the semi-perimeter of the triangle, \( s = \frac{a + b + c}{2} \), and \( a \), \( b \), and \( c \) are the lengths of the sides.
- Using Two Sides and the Included Angle: If two sides and the included angle are known, the area can be found using: \[ A = \frac{1}{2} \times a \times b \times \sin(C) \] where \( a \) and \( b \) are the lengths of the sides, and \( C \) is the included angle.
- Equilateral Triangle: For an equilateral triangle with side length \( a \), the formula is: \[ A = \frac{\sqrt{3}}{4} \times a^2 \]
- Isosceles Triangle: For an isosceles triangle with equal sides \( a \) and base \( b \): \[ A = \frac{b}{4} \sqrt{4a^2 - b^2} \]
These formulas help in calculating the area of different types of triangles accurately and efficiently.
Formulas for Perimeter
Calculating the perimeter of a triangle involves adding the lengths of its sides. This applies to all types of triangles, including equilateral, isosceles, and scalene triangles.
General Formula
For any triangle with sides \(a\), \(b\), and \(c\), the perimeter \(P\) is given by:
\[
P = a + b + c
\]
Equilateral Triangle
An equilateral triangle has all three sides equal. If the length of each side is \(a\), then the perimeter is:
\[
P = 3a
\]
Isosceles Triangle
An isosceles triangle has two sides of equal length. If the lengths of the two equal sides are \(a\) and the third side is \(b\), then the perimeter is:
\[
P = 2a + b
\]
Scalene Triangle
A scalene triangle has all sides of different lengths. The perimeter is simply the sum of all three sides:
\[
P = a + b + c
\]
Right Triangle
For a right triangle, where \(a\) and \(b\) are the lengths of the legs and \(c\) is the hypotenuse, the perimeter is:
\[
P = a + b + c
\]
The hypotenuse \(c\) can be found using the Pythagorean theorem:
\[
c = \sqrt{a^2 + b^2}
\]
By using these formulas, you can easily find the perimeter of any triangle, whether it is equilateral, isosceles, scalene, or right-angled.
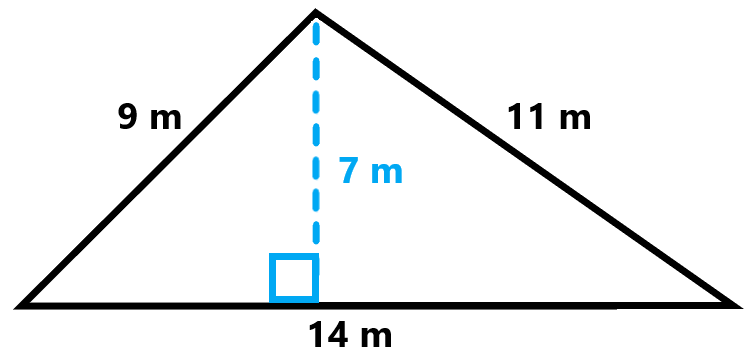
Step-by-Step Examples
Understanding how to find the area and perimeter of a triangle is essential in geometry. Here are detailed examples to help you master these concepts.
Example 1: Finding the Area of a Right Triangle
Given a right triangle with a base of 8 cm and a height of 6 cm, we can find the area using the formula:
- Write down the formula for the area: \( A = \frac{1}{2} \times \text{base} \times \text{height} \)
- Identify the dimensions: base = 8 cm, height = 6 cm
- Substitute the dimensions into the formula:
- \( A = \frac{1}{2} \times 8 \times 6 = 24 \, \text{cm}^2 \)
Example 2: Finding the Perimeter of a Scalene Triangle
For a scalene triangle with sides of 9 yards, 11 yards, and 13 yards, the perimeter is calculated as follows:
- Add up the lengths of all sides: \( P = 9 + 11 + 13 = 33 \, \text{yards} \)
Example 3: Area Using Heron's Formula
Given a triangle with sides of 5 m, 6 m, and 7 m, use Heron's formula to find the area:
- Calculate the semi-perimeter: \( s = \frac{a+b+c}{2} = \frac{5+6+7}{2} = 9 \, \text{m} \)
- Substitute into Heron's formula:
- \( A = \sqrt{s(s-a)(s-b)(s-c)} = \sqrt{9(9-5)(9-6)(9-7)} = \sqrt{9 \times 4 \times 3 \times 2} = \sqrt{216} = 14.7 \, \text{m}^2 \)
Example 4: Finding the Perimeter Using Algebra
Consider a triangle with a given perimeter of 118 km and sides defined algebraically:
- Side YA = 2x + 5
- Side YK = 6x - 10
- Side AK = 4x + 15
- Set up the equation: \( 2x + 5 + 6x - 10 + 4x + 15 = 118 \)
- Simplify and solve for x: \( 12x + 10 = 118 \) \( \Rightarrow 12x = 108 \) \( \Rightarrow x = 9 \, \text{km} \)
- Calculate each side: YA = 23 km, YK = 44 km, AK = 51 km
- Confirm the perimeter: \( 23 + 44 + 51 = 118 \, \text{km} \)
Applications and Real-life Examples
The concepts of finding the area and perimeter of a triangle have numerous practical applications in various fields. Below are detailed examples of how these calculations are used in real life.
-
Finding the Area and Perimeter in Construction
In construction, accurately determining the area and perimeter of triangular sections is crucial for various tasks such as material estimation and land measurement.
- Architects use these calculations to design triangular components of buildings.
- Surveyors calculate the area to determine the amount of land needed for construction projects.
- Builders use perimeter calculations to estimate the length of materials required, such as fencing or trim.
Example:
Consider a triangular plot of land with sides measuring 50m, 60m, and 70m. To find the area using Heron's Formula:
- First, calculate the semi-perimeter (s):
- Next, use the formula:
\( s = \frac{50 + 60 + 70}{2} = 90 \) meters
\( \text{Area} = \sqrt{s(s - a)(s - b)(s - c)} \)
\( \text{Area} = \sqrt{90(90 - 50)(90 - 60)(90 - 70)} \)
\( \text{Area} = \sqrt{90 \times 40 \times 30 \times 20} \)
\( \text{Area} = \sqrt{2160000} \approx 1469.69 \) square meters
-
Applications in Landscaping and Design
Landscapers and designers often work with triangular plots or features within larger designs.
- Landscape architects calculate areas to plan for planting, water features, and pathways.
- Designers use perimeter calculations to layout walkways, borders, and fencing accurately.
- These measurements ensure efficient use of space and resources.
Example:
For a triangular garden bed with a base of 8m and a height of 5m, the area is calculated as:
- Using the base and height method:
\( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \)
\( \text{Area} = \frac{1}{2} \times 8 \times 5 = 20 \) square meters
Practice Problems
To help solidify your understanding of finding the area and perimeter of triangles, here are some practice problems. Each problem is designed to challenge your grasp of the concepts and formulas discussed. Use the given measurements to solve for either the area or the perimeter, and refer to the formulas as needed.
Area Practice Problems
-
Given a triangle with a base of 5 cm and a height of 10 cm, find the area.
Area = \frac{1}{2} \times base \times height = \frac{1}{2} \times 5 \, cm \times 10 \, cm = 25 \, cm^2 -
A right triangle has legs measuring 6 cm and 8 cm. Find the area.
Area = \frac{1}{2} \times base \times height = \frac{1}{2} \times 6 \, cm \times 8 \, cm = 24 \, cm^2 -
Calculate the area of an equilateral triangle with a side length of 10 cm.
Area = \frac{\sqrt{3}}{4} \times side^2 = \frac{\sqrt{3}}{4} \times 10^2 \, cm^2 = 25\sqrt{3} \, cm^2 \approx 43.3 \, cm^2 -
Using Heron's formula, find the area of a triangle with sides 7 cm, 8 cm, and 9 cm.
s = \frac{a + b + c}{2} = \frac{7 \, cm + 8 \, cm + 9 \, cm}{2} = 12 \, cm Area = \sqrt{s(s-a)(s-b)(s-c)} = \sqrt{12(12-7)(12-8)(12-9)} = \sqrt{12 \times 5 \times 4 \times 3} = \sqrt{720} \approx 26.8 \, cm^2
Perimeter Practice Problems
-
Find the perimeter of a triangle with sides measuring 3 cm, 4 cm, and 5 cm.
Perimeter = a + b + c = 3 \, cm + 4 \, cm + 5 \, cm = 12 \, cm -
An equilateral triangle has a side length of 9 cm. Calculate its perimeter.
Perimeter = 3 \times side = 3 \times 9 \, cm = 27 \, cm -
Determine the perimeter of an isosceles triangle with two sides measuring 7 cm each and a base of 10 cm.
Perimeter = 2a + b = 2 \times 7 \, cm + 10 \, cm = 24 \, cm -
Find the perimeter of a scalene triangle with sides of 6 cm, 8 cm, and 10 cm.
Perimeter = a + b + c = 6 \, cm + 8 \, cm + 10 \, cm = 24 \, cm
Use these problems to test your knowledge and improve your skills. Try solving each one step-by-step, and check your answers against the provided solutions.
Frequently Asked Questions
Below are some common questions about finding the area and perimeter of triangles:
- Can the area of a triangle be negative?
No, the area of a triangle cannot be negative. Area represents a physical space, which cannot have a negative value.
- Can a triangle have a perimeter of zero?
No, a triangle cannot have a zero perimeter. A triangle with zero perimeter does not exist because it means all its sides have zero lengths, which contradicts the definition of a triangle.
- What if I know the lengths of the sides of the triangle, but not the height?
You can use Heron's formula to calculate the area of a triangle when the lengths of all three sides are known. This formula does not require the height.
Heron's formula is given by:
\[
A = \sqrt{s(s-a)(s-b)(s-c)}
\]
where \(s = \frac{a+b+c}{2}\) is the semi-perimeter and \(a\), \(b\), and \(c\) are the sides of the triangle. - Is the perimeter of a triangle always greater than its area?
Not necessarily. The relationship between a triangle’s area and its perimeter depends on the unit of measurement and the size of the triangle.
- What is the formula for the perimeter of a triangle?
The perimeter of a triangle is the sum of the lengths of its three sides. The formula is:
\[
P = a + b + c
\]
where \(a\), \(b\), and \(c\) are the lengths of the sides. - What is the area and perimeter of an equilateral triangle?
The area of an equilateral triangle is given by:
\[
A = \frac{\sqrt{3}}{4} a^2
\]
And the perimeter is:\[
P = 3a
\]
where \(a\) is the length of a side. - How do you calculate the area of a triangle?
The area of a triangle can be calculated using the base and height:
\[
A = \frac{1}{2} \times \text{base} \times \text{height}
\]
This formula works for any type of triangle if the base and height are known.
Video hướng dẫn cách tìm diện tích và chu vi của tam giác một cách dễ hiểu và chi tiết. Phù hợp cho học sinh và giáo viên.
Làm thế nào để Tìm Diện Tích và Chu Vi của Tam Giác | Toán với Mr. J
READ MORE:
Video hướng dẫn cách tìm diện tích và chu vi của tam giác một cách chi tiết và dễ hiểu, giúp học sinh nắm vững kiến thức toán học cơ bản.
Làm thế nào để Tìm Diện Tích và Chu Vi của Tam Giác