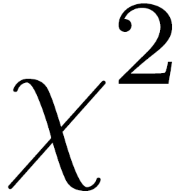Topic x squared negative: The concept of "x squared negative" plays a crucial role in various mathematical contexts. Understanding it is essential for solving quadratic equations, analyzing functions, and exploring mathematical theories. This article delves into the nuances of negative x squared, providing insights into its applications, properties, and significance in different fields of study.
Table of Content
Understanding Negative Squares in Quadratic Equations
The concept of negative squares often appears in quadratic equations and is essential for students learning algebra and higher mathematics. This guide provides a detailed overview of how negative squares work, their implications in quadratic equations, and how to solve related problems.
Squaring Negative Numbers
When you square a negative number, the result is positive. This is because multiplying two negative numbers results in a positive product. For example:
- (-3)² = (-3) * (-3) = 9
- (-5)² = (-5) * (-5) = 25
Quadratic Equations with Negative Coefficients
Quadratic equations often involve negative coefficients. The general form of a quadratic equation is:
\[ ax^2 + bx + c = 0 \]
If \( a \) is negative, the parabola opens downwards. For example, consider the equation:
\[ -x^2 - 3x + 10 = 0 \]
To solve such equations, you can use the quadratic formula:
\[ x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{2a} \]
Where \( a = -1 \), \( b = -3 \), and \( c = 10 \).
Steps to Solve Quadratic Equations
- Identify the coefficients \( a \), \( b \), and \( c \).
- Calculate the discriminant: \( b^2 - 4ac \).
- Determine the roots using the quadratic formula.
Graphing Quadratic Equations
Graphing a quadratic equation with a negative leading coefficient results in a parabola that opens downwards. Here is a step-by-step process to graph such an equation:
- Find the vertex using the formula: \[ x = -\frac{b}{2a} \]
- Calculate the y-intercept by evaluating the equation at \( x = 0 \).
- Plot additional points on either side of the vertex to ensure accuracy.
- Draw the parabola through these points, ensuring it opens downwards.
Examples and Exercises
To reinforce the concepts, here are a few exercises:
- Solve \( -2x^2 + 4x - 6 = 0 \)
- Graph \( -x^2 + 2x + 3 \) and identify its vertex and intercepts.
Conclusion
Understanding how negative squares function in quadratic equations is crucial for solving and graphing these equations accurately. Practice with different forms and coefficients to master this concept.

READ MORE:
Introduction to Negative X Squared
Negative \(x^2\), written as \(-x^2\), represents the negation of the square of a variable \(x\). This concept appears frequently in various fields of mathematics and physics. Understanding \(-x^2\) involves knowing how squaring and negation interact and the implications of these operations in different contexts.
In mathematics, squaring a number, whether positive or negative, always yields a positive result. For instance, \( (-3)^2 = 9 \). However, when a negative sign is applied outside the square, as in \(-x^2\), it indicates that the result of the squaring operation should be negated. For example, \(-3^2\) would be calculated as \( -(3^2) = -9 \). This distinction is crucial in correctly interpreting mathematical expressions.
In physics, \(-x^2\) can be used to describe scenarios where a value decreases as the square of a variable increases. One such application is in potential energy fields, where the potential energy might be represented as a function of \(-x^2\). Similarly, in economics, \(-x^2\) might model depreciation or loss of value over time, reflecting a rapid decline as a variable increases.
Here are some key points to consider about \(-x^2\):
- When \(-x^2\) is graphed, it forms a downward-opening parabola, indicating that the values decrease as \(x\) moves away from zero in either direction.
- In equations, \(-x^2\) often represents an opposing force or a diminishing return, providing insight into systems where growth is counteracted by another factor.
- The correct interpretation of \(-x^2\) is vital in solving quadratic equations, particularly in determining the nature and behavior of their solutions.
In conclusion, the concept of \(-x^2\) is fundamental in both theoretical and applied mathematics, offering insights into the nature of various physical, economic, and abstract systems. Mastery of this concept aids in the analysis and understanding of numerous complex scenarios.
Basic Concepts
The concept of negative x squared is fundamental in mathematics and has applications in various fields such as physics, economics, and finance. When we talk about x squared, we are referring to the expression \( x^2 \), which represents the area of a square with side length \( x \). However, when the term is negative, as in -x squared (\( -x^2 \)), it introduces unique properties and implications.
- Mathematical Representation: The expression \( -x^2 \) is mathematically defined as the negative value of the square of \( x \). If \( x \) is any real number, squaring it will always give a positive result, but the negative sign in front makes the entire expression negative.
- Quadratic Equations: In the context of quadratic equations, the term \( -x^2 \) can affect the direction of the parabola. A standard quadratic equation is \( ax^2 + bx + c = 0 \). If \( a \) is negative, the parabola opens downward, which indicates a maximum value at its vertex.
- Physics Applications: In physics, negative \( x^2 \) is often used to represent potential energy in force fields. For instance, the potential energy of a particle in a gravitational field can be modeled using negative quadratic terms.
- Economic and Financial Models: In economics, negative \( x^2 \) can represent the depreciation of assets over time. In finance, it can denote the cost of options with negative value, demonstrating loss scenarios.
| Concept | Explanation |
| Mathematical Representation | The negative value of the square of \( x \), expressed as \( -x^2 \). |
| Quadratic Equations | Influences the direction of the parabola in the equation \( ax^2 + bx + c = 0 \). |
| Physics Applications | Represents potential energy in force fields, such as gravitational fields. |
| Economic Models | Models asset depreciation and loss scenarios in finance. |
Understanding the concept of negative \( x^2 \) is crucial for solving complex mathematical problems and applying these principles in real-world scenarios across different domains.
Mathematical Properties
Understanding the mathematical properties of negative \(x\) squared is crucial for various applications in mathematics and science. Below are detailed explanations of these properties:
- Definition: Negative \(x\) squared, written as \(-x^2\), means the negative of the square of \(x\). For example, if \(x = 3\), then \(-x^2 = -(3^2) = -9\).
- Computation Rules:
- If \(x\) is a positive number, \(-x^2\) is always negative. For instance, for \(x = 2\), \(-x^2 = -4\).
- If \(x\) is a negative number, \(-x^2\) is also negative. For example, for \(x = -2\), \(-x^2 = -4\).
- The negative sign outside the square operation indicates that the squaring happens first, followed by the negation. Hence, \(-3^2 = -(3^2) = -9\).
- Graphical Representation: The graph of \(y = -x^2\) is a downward-opening parabola, indicating that for all values of \(x\), \(y\) will be non-positive.
- Applications:
- In physics, \(-x^2\) can represent potential energy fields, such as the gravitational potential energy in a system where the potential decreases as the distance increases.
- In economics, \(-x^2\) can model scenarios of diminishing returns or losses, where the rate of loss increases quadratically with the increase in some variable \(x\).
- Quadratic Equations:
The general form of a quadratic equation is \(ax^2 + bx + c = 0\). If \(a < 0\), the quadratic term will be negative, leading to a downward-opening parabola. The solutions to this equation can be found using the quadratic formula:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]The discriminant \(b^2 - 4ac\) determines the nature of the roots, whether they are real or complex.
Applications in Mathematics
Negative \( x^2 \) appears in various mathematical contexts, primarily in quadratic equations and graphs. Below are some of the key applications:
- Quadratic Graphs with Negative \( x^2 \)
- Solving Quadratic Equations Using Negative \( x^2 \)
When the quadratic term in a function is negative, it results in a downward-opening parabola. This property is useful in various applications, such as physics and engineering, where it can represent maximum points or the shape of certain objects.
Consider the quadratic function \( f(x) = -x^2 + bx + c \). The graph of this function is a parabola that opens downward:
Using MathJax, the vertex of the parabola can be calculated as follows:
\[
x_{\text{vertex}} = -\frac{b}{2a}
\]
Given \( a = -1 \), the vertex formula becomes:
\[
x_{\text{vertex}} = \frac{b}{2}
\]
Quadratic equations of the form \( ax^2 + bx + c = 0 \) where \( a < 0 \) have unique characteristics. These equations can be solved using the quadratic formula:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
When \( a \) is negative, it affects the direction of the parabola, making the solutions (roots) represent the x-values where the function crosses the x-axis. This property is crucial in finding maximum values in optimization problems.
For example, solving \( -x^2 + 4x - 3 = 0 \) involves calculating:
\[
x = \frac{-4 \pm \sqrt{4^2 - 4(-1)(-3)}}{2(-1)} = \frac{-4 \pm \sqrt{16 - 12}}{-2} = \frac{-4 \pm 2}{-2}
\]
Thus, the solutions are:
\[
x = 1 \quad \text{and} \quad x = 3
\]

Applications in Other Fields
Negative \(x^2\) terms play significant roles in various fields beyond pure mathematics. Here are some key applications:
Use in Physics and Engineering
-
Gravitational Fields: In physics, the concept of potential energy in a gravitational field can be modeled using quadratic functions. For example, the potential energy (\(U\)) near the Earth's surface can be expressed as \(U = -mgx^2\), where \(m\) is mass, \(g\) is the gravitational constant, and \(x\) is the height. This shows how the negative \(x^2\) term indicates that the potential energy decreases with height.
-
Projectile Motion: The height (\(y\)) of a projectile at time (\(t\)) can be modeled using the equation \(y = -\frac{1}{2}gt^2 + v_0t + y_0\), where \(g\) is the acceleration due to gravity, \(v_0\) is the initial velocity, and \(y_0\) is the initial height. The negative \(t^2\) term indicates the downward acceleration due to gravity.
Financial Mathematics: Representing Losses and Costs
-
Profit Maximization: In economics, quadratic functions are used to model profit and cost functions. For instance, the profit (\(P\)) might be expressed as a function of the quantity produced (\(q\)), such as \(P = -aq^2 + bq - c\), where \(a\), \(b\), and \(c\) are constants. The negative \(q^2\) term reflects decreasing returns to scale, indicating that beyond a certain point, increasing production leads to a decrease in profit.
-
Cost Functions: Similarly, cost functions can be quadratic, where the total cost (\(C\)) is given by \(C = aq^2 + bq + c\). In this context, the positive \(q^2\) term represents increasing marginal costs, meaning the cost of producing each additional unit rises as production increases.
Common Misconceptions
-
Misunderstanding the difference between \(-x^2\) and \((-x)^2\): One common misconception is confusing \(-x^2\) with \((-x)^2\). The expression \(-x^2\) means the negative of \(x\) squared, which results in \(-x^2\). In contrast, \((-x)^2\) means the square of negative \(x\), which results in \(x^2\).
-
Incorrect application of the square root property: Another misconception is thinking that \(\sqrt{x^2}\) is always \(\pm x\). In reality, \(\sqrt{x^2}\) is \(|x|\) because the square root function only returns the non-negative root. When solving equations like \(x^2 = a\), one should write \(x = \pm \sqrt{a}\) to account for both positive and negative solutions.
-
Assuming negative exponents result in negative numbers: Negative exponents do not make the result negative. Instead, they represent the reciprocal of the base raised to the positive exponent. For example, \(x^{-2} = \frac{1}{x^2}\), not \(-x^2\).
-
Misinterpreting the role of negative coefficients in quadratic equations: Some might think that a negative coefficient in front of \(x^2\) in a quadratic equation only affects the solutions' signs. However, it actually affects the graph's orientation, causing it to open downward, and influences the nature of the solutions.
-
Confusing the properties of negative and complex numbers: When dealing with negative values under square roots, students often mistake them as undefined in the real number system. Instead, these values belong to the complex number system, where \(\sqrt{-1} = i\), and thus \(\sqrt{-x^2} = ix\).
Further Reading and Resources
-
Quadratic Equations and Graphs: Understanding the fundamentals of quadratic equations and their graphical representations is crucial for mastering negative x squared concepts.
-
Exponents and Negative Numbers: A thorough understanding of how exponents and negative numbers interact is vital for working with negative x squared.
-
Advanced Algebraic Concepts: Explore more advanced topics in algebra to deepen your understanding of negative x squared and its applications.
Phân Tích Nhân Tử Bậc Hai (Âm X Bình Phương) (2-PHÚT TOÁN HỌC!)
READ MORE:
Hoàn Thành Bình Phương Bằng Cách Phân Tích Nhân Tử Âm Một



:max_bytes(150000):strip_icc()/Chi-SquareStatistic_Final_4199464-7eebcd71a4bf4d9ca1a88d278845e674.jpg)