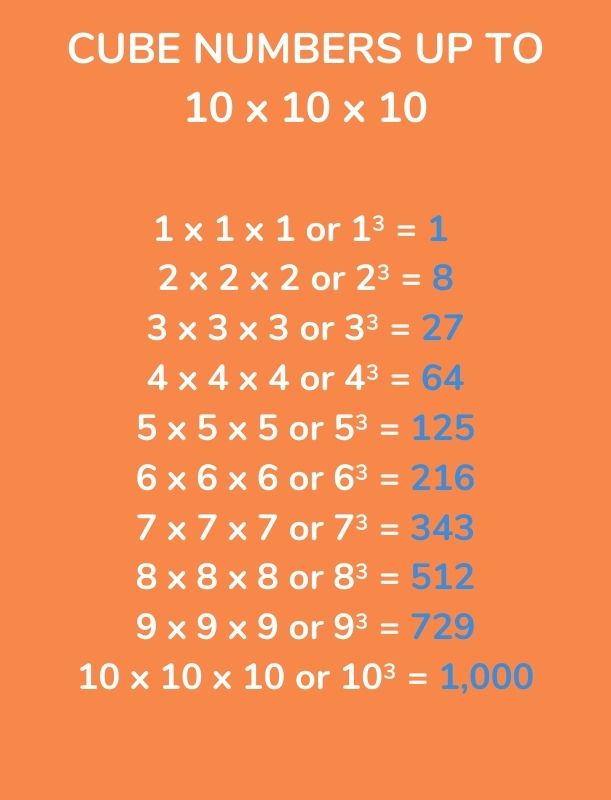3 Square Root of 343: Discovering the Magic Number

To determine the cube root of 343, we are essentially finding a number that, when multiplied by itself three times, equals 343. Using mathematical notation, this can be expressed as:

$$


343

1
3

Or more simply, $$

3
343

.

Through calculation, we find that:

$$

3
√
343
=
7

This means that 7 is the cube root of 343 because:

$$

7
×
7
×
7
=
343

Thus, we can conclude:

The cube root of 343 is 7.

The concept of cube roots is an essential part of mathematics, particularly in algebra and number theory. A cube root of a number is a value that, when multiplied by itself three times, gives the original number. Mathematically, if $x^3$ = $a$, then $x$ is the cube root of $a$.

To better understand cube roots, let's explore their properties and calculation methods step-by-step:

1. Basic Definition: The cube root of a number $a$ is a number $x$ such that $x^3=a$. It is denoted as $a^{\frac{1}{3}}$ or $\sqrt[3]{a}$.

2. Examples: For example, the cube root of 27 is 3 because $3^3=27$. Similarly, the cube root of 8 is 2 because $2^3=8$.

3. Calculation: Calculating cube roots can be done using various methods, including prime factorization, estimation, and the use of calculators. For instance, to find the cube root of 343, we can recognize that $343=7^3$, thus the cube root of 343 is 7.

4. Properties: Cube roots have several properties that are useful in different mathematical contexts:
   

   
   
   • Real Numbers: Every real number has exactly one real cube root.
   
   
   • Negative Numbers: The cube root of a negative number is also negative.
   
   
   • Complex Numbers: In the realm of complex numbers, every number has three cube roots.
   
   
   
   



5. Applications: Cube roots are used in various fields such as geometry (finding volumes), physics (calculating densities), and engineering (solving cubic equations).

Understanding cube roots is fundamental for progressing in higher-level mathematics and for practical problem-solving in various scientific disciplines.

The concept of cube roots is an integral part of mathematics, particularly in algebra and geometry. A cube root of a number is a value that, when multiplied by itself three times, results in the original number. In mathematical terms, if $x^3$ equals $a$, then $x$ is the cube root of $a$.

To gain a comprehensive understanding of cube roots, let's break down the concept step-by-step:

1. Basic Definition: The cube root of a number $a$ is a number $x$ such that $x^3=a$. This is represented as $\sqrt[3]{a}$ or $a^{\frac{1}{3}}$.

2. Examples:
   

   
   
   • The cube root of 8 is 2 because $2^3=8$.
   
   
   • The cube root of 27 is 3 because $3^3=27$.
   
   
   • The cube root of 343 is 7 because $7^3=343$.
   
   
   
   



3. Properties:
   

   
   
   • Uniqueness: Every real number has a unique real cube root.
   
   
   • Sign: The cube root of a negative number is also negative. For example, the cube root of -8 is -2 because ${-}^2=-8$.
   
   
   • Complex Numbers: In complex numbers, every number has three cube roots.
   
   
   
   



4. Calculation Methods:
   

   
   
   • Prime Factorization: Decomposing a number into its prime factors can help in finding the cube root.
   
   
   • Estimation: Using approximation methods to find a close value, which can be refined through iterations.
   
   
   • Calculators: Modern calculators and computer software can quickly compute cube roots.
   
   
   
   



5. Applications: Cube roots are used in various fields, including:
   

   
   
   • Geometry: Calculating volumes of cubes and other three-dimensional objects.
   
   
   • Physics: Determining densities and other properties of materials.
   
   
   • Engineering: Solving cubic equations and modeling real-world phenomena.
   
   
   
   

By understanding cube roots, one can solve a wide range of mathematical problems and apply this knowledge to practical situations in science and engineering.

In mathematics, the cube root of a number is a special value that, when used in a multiplication three times, gives that number. If we denote the number as $a$, then the cube root of $a$ is a number $x$ such that $x^3=a$.

The cube root can be represented in several ways:

• Using the radical symbol: $\sqrt[3]{a}$
• Using fractional exponents: $a^{\frac{1}{3}}$

To illustrate, let's consider the cube root of 343:

1. Express the problem: $\sqrt[3]{343}or{343}^{\frac{1}{3}}$

2. Identify the number whose cube is 343. Since $7^3=343$, the cube root of 343 is 7.

Formally, this can be defined as:

If $x^3=a$, then $x$ is the cube root of $a$. This can be written as:

$$


a
3

=

a

1
3


=
x

Cube roots have unique properties:

• Every positive real number has one positive real cube root.
• Every negative real number has one negative real cube root.
• In the complex number system, every non-zero number has three cube roots.

Understanding the mathematical definition of cube roots is crucial for solving various algebraic problems and for applications in science and engineering.

Calculating the cube root of a number involves finding a value that, when multiplied by itself three times, gives the original number. Let's calculate the cube root of 343 step-by-step:

1. Express the Problem: We need to find the cube root of 343. Mathematically, this can be written as $\sqrt[3]{343}or{343}^{\frac{1}{3}}$.

2. Prime Factorization: One method to find the cube root is to use prime factorization. First, factorize 343 into its prime factors.

   • 343 is not divisible by 2 (since it's odd).
   • 343 is not divisible by 3 (sum of digits is 10, not divisible by 3).
   • 343 is divisible by 7: $343÷7=49$.
   • 49 is also divisible by 7: $49÷7=7$.
   • Thus, $343=7^3$.

3. Identify the Cube Root: Since $7^3=343$, the cube root of 343 is 7.

4. Verification: To verify, multiply 7 by itself three times:
   

   
   
   • $7\times 7=49$
   
   
   • $49\times 7=343$
   
   
   
   

Therefore, the cube root of 343 is confirmed to be 7.

After calculating the cube root of 343 and determining it to be 7, it is essential to verify this result. Verification ensures that the calculation is correct and accurate. Here is a step-by-step process to verify the cube root of 343:

1. Express the Cube Root: We have determined that the cube root of 343 is 7. Mathematically, this means:

   $\sqrt[3]{343}=7$ or ${343}^{\frac{1}{3}}=7$.

2. Cube the Result: To verify, we need to cube the result (7) and check if it equals 343:

   • First multiplication: $7\times 7=49$
   • Second multiplication: $49\times 7=343$

3. Check the Result: Since $7^3=343$, our initial calculation is confirmed to be correct.

4. Alternative Verification Method: Another way to verify is to use a calculator:
   

   
   
   • Enter 343 and apply the cube root function.
   
   
   • The calculator should display 7.
   
   
   
   

By following these steps, we have verified that the cube root of 343 is indeed 7. This verification process ensures the accuracy and reliability of our calculations, reinforcing our understanding of cube roots.

Cube roots have numerous practical applications across various fields, including mathematics, engineering, physics, and computer science. Understanding how to calculate and apply cube roots can be immensely beneficial. Here are some key practical applications:

• Engineering and Architecture: Cube roots are essential in calculating volumes and dimensions of three-dimensional structures. For instance, determining the side length of a cube when given its volume requires finding the cube root of the volume.
• Physics: In physics, cube roots are used to solve problems related to the volume and density of objects. For example, to find the side length of a cubic object given its volume, one needs to compute the cube root of the volume.
• Computer Graphics: In computer graphics, cube roots are utilized in 3D modeling and rendering to scale objects proportionally. This helps in maintaining the correct dimensions and proportions in virtual environments.
• Economics: In economics, cube roots can be used to model certain types of economic growth and decay, particularly when dealing with cubic equations and models that involve three-dimensional data.
• Pharmacy: In pharmaceutical calculations, cube roots are often used to determine the appropriate dosages of medications when dealing with volume and concentration measurements.

Here is an example illustrating the practical use of cube roots in determining the dimensions of a cubic container:

1. Given a cubic container with a volume of 343 cubic units, we need to find the side length of the container.
2. The formula for the volume of a cube is \( V = s^3 \), where \( s \) is the side length.
3. To find the side length, we need to calculate the cube root of the volume: \( s = \sqrt[3]{343} \).
4. Calculating the cube root, we get \( s = 7 \). Therefore, the side length of the cubic container is 7 units.

Cube roots also play a significant role in scientific research, particularly in fields that involve volumetric data and three-dimensional modeling. Mastery of cube root calculations can enhance problem-solving skills and enable more precise and accurate measurements in various practical applications.

Calculating cube roots can be challenging, especially when dealing with non-perfect cubes. Here are some common mistakes to avoid:

• Incorrect Factorization: One common mistake is incorrect factorization. Ensure that the number is properly broken down into its prime factors. For example, \(343 = 7^3\), which simplifies to 7. Incorrect factorization can lead to incorrect results.
• Ignoring Negative Signs: When working with cube roots, it's essential to remember that negative numbers have real cube roots. For instance, \(\sqrt[3]{-343} = -7\). Neglecting the negative sign can result in incorrect answers.
• Using Square Root Methods: Confusing cube root calculations with square root methods can lead to errors. Remember that the process for finding cube roots is different from finding square roots.
• Rounding Errors: While approximations can be useful, excessive rounding can lead to inaccuracies. It’s important to carry sufficient decimal places through the calculations to ensure precision.
• Calculator Misuse: Misusing calculator functions or using the wrong mode can lead to incorrect answers. Ensure you are using the cube root function correctly. On most calculators, this function is denoted as \(\sqrt[3]{x}\).

To avoid these mistakes, follow a step-by-step approach:

1. Factor the Number: Start by breaking down the number into its prime factors. For example, \(343 = 7 \times 7 \times 7\).
2. Identify the Cube Root: Once the prime factors are identified, determine the cube root. In this case, \(\sqrt[3]{343} = 7\).
3. Verify the Result: Verify your result by cubing the answer. \(7^3 = 343\), confirming the cube root is correct.

By following these steps and being mindful of common mistakes, you can accurately calculate cube roots and apply them effectively in various mathematical problems.

Finding the cube root of a number, especially non-perfect cubes, can be complex. Here are some advanced methods to calculate cube roots efficiently:

• Prime Factorization Method: This method involves breaking down the number into its prime factors. For example, the prime factorization of 343 is \(7 \times 7 \times 7\) or \(7^3\). The cube root of \(7^3\) is \(7\).
• Newton's Method (Newton-Raphson Method): This iterative method is useful for finding approximations of cube roots. Given a number \(x\), you start with an initial guess \(a\) and refine it using the formula: \[ a_{n+1} = \frac{1}{3} \left( \frac{x}{a_n^2} + 2a_n \right) \] This process is repeated until the value stabilizes.
• Logarithms: Cube roots can be calculated using logarithms and exponentiation. If you know the logarithm of a number, you can find the cube root by dividing the logarithm by 3 and then exponentiating the result: \[ \sqrt[3]{x} = 10^{\frac{\log_{10}(x)}{3}} \]
• Using Mathematical Software: Tools like MATLAB, Mathematica, and programming languages with numerical libraries (e.g., Python with NumPy) can compute cube roots with high precision. For example, in Python, you can use:

  import numpy as np
  cube_root = np.cbrt(343)

These advanced methods provide efficient ways to compute cube roots, whether you are dealing with perfect cubes or more complex numbers.

The cube root of 343, which is 7, demonstrates the fascinating properties and applications of cube roots in mathematics and various real-world contexts. Understanding the process of finding cube roots, whether through simple methods like prime factorization or advanced techniques like Newton's method, equips us with essential skills for tackling complex mathematical problems.

Here are the key takeaways from our exploration of cube roots:

• Definition and Calculation: The cube root of a number is a value that, when multiplied by itself three times, gives the original number. For 343, the cube root is \( \sqrt[3]{343} = 7 \).
• Common Mistakes: It's important to avoid errors such as incorrect factorization, ignoring negative signs, and rounding errors. Accurate calculations ensure reliable results.
• Practical Applications: Cube roots are widely used in engineering, physics, computer graphics, economics, and pharmacy. They help in solving problems related to volumes, dimensions, scaling, and growth models.
• Advanced Methods: Techniques like Newton's method, logarithms, and mathematical software provide efficient ways to find cube roots, especially for non-perfect cubes.

Mastering the concept of cube roots not only enhances mathematical proficiency but also opens up opportunities to apply these skills in various scientific and practical domains. With practice and a clear understanding of the underlying principles, anyone can become adept at calculating and utilizing cube roots effectively.

• What is the cube root of 343?

  The cube root of 343 is 7, because \(7^3 = 343\).

• How do you calculate the cube root of 343?

  You can calculate the cube root of 343 by finding the number that, when multiplied by itself three times, equals 343. In this case, \(7 \times 7 \times 7 = 343\).

• What are the practical applications of knowing cube roots?

  Cube roots are used in various fields such as engineering, physics, and computer science. They are essential in solving volume-related problems and in understanding the scaling of physical quantities.

• What is the difference between a square root and a cube root?

  A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because \(3^2 = 9\). A cube root is a value that, when used three times in a multiplication, gives the original number. For example, the cube root of 343 is 7 because \(7^3 = 343\).

• Can cube roots be negative?

  Yes, cube roots can be negative. For example, the cube root of -343 is -7 because \((-7)^3 = -343\).

• How do you find the cube root of a non-perfect cube?

  To find the cube root of a non-perfect cube, you can use methods like estimation, prime factorization, or a scientific calculator. Estimation involves finding two consecutive perfect cubes between which the number lies and then interpolating to find the approximate cube root.

• Are there advanced methods for calculating cube roots?

  Yes, advanced methods include the Newton-Raphson method and using logarithms. These methods provide more precise results and are useful for large numbers or when high precision is required.