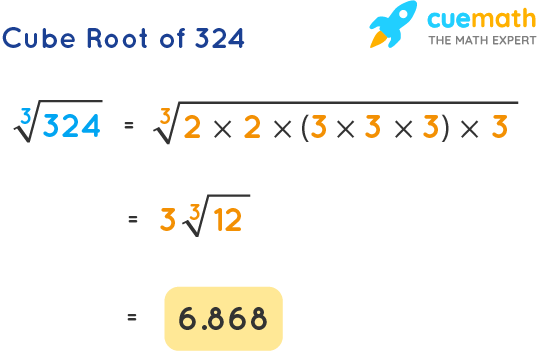
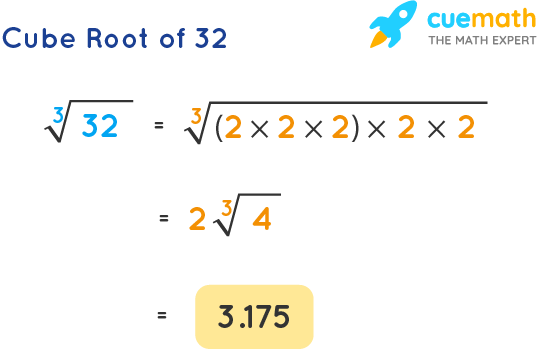
Topic what is the cubed root of 3: The cubed root of 3, a fundamental concept in mathematics, is key to solving various problems in geometry, physics, and algebra. Understanding its value and applications can enhance your mathematical skills and provide insights into cubic relationships. Explore how to calculate it, its significance, and where it is applied in real-world scenarios.
Table of Content
- The Cubed Root of 3
- Introduction to Cubed Roots
- Understanding the Cubed Root of 3
- Approximate Value and Calculation Methods
- Using Calculators and Software
- Manual Calculation Techniques
- Applications of the Cubed Root of 3
- Geometric Interpretations
- Physics and Engineering Applications
- Algebraic Equations Involving Cubic Roots
- Advanced Mathematical Concepts
- Real-World Examples
- Visual Representations
- Common Mistakes and Misconceptions
- Practice Problems and Solutions
- Summary and Conclusion
- YOUTUBE: Video Giới thiệu về Căn bậc ba với Thầy J cung cấp một cách hiểu đơn giản và rõ ràng về khái niệm căn bậc ba.
The Cubed Root of 3
The cubed root of a number \( n \) is a number \( x \) such that \( x^3 = n \). For the number 3, the cubed root is denoted as \( \sqrt[3]{3} \) or \( 3^{\frac{1}{3}} \).
Mathematical Representation
The cubed root of 3 can be represented mathematically as:
\[ \sqrt[3]{3} = 3^{\frac{1}{3}} \]
Approximate Value
The approximate value of \( \sqrt[3]{3} \) is:
\[ \sqrt[3]{3} \approx 1.4422495703 \]
Steps to Calculate the Cubed Root of 3
- Identify the number for which you want to find the cubed root (in this case, 3).
- Use a calculator or a mathematical method to find the cubed root.
- Verify the result by cubing the approximate value to see if it equals 3.
Applications
- Geometry: Calculating the side length of a cube with a volume of 3 cubic units.
- Physics: Understanding relationships in cube root laws in various phenomena.
- Mathematics: Solving algebraic equations involving cubic terms.
Visual Representation
A cube with a volume of 3 cubic units would have a side length of approximately \( 1.442 \) units:
| Volume | Side Length |
| 3 cubic units | \( \sqrt[3]{3} \approx 1.442 \) units |
Understanding the cubed root of 3 is essential in various scientific and mathematical fields, providing insight into cubic relationships and aiding in solving complex equations.

READ MORE:
Introduction to Cubed Roots
The cubed root of a number is a value that, when multiplied by itself three times, gives the original number. It is an essential concept in mathematics, particularly in algebra, geometry, and real-world applications. The cubed root is represented using the radical symbol with an index of three, or using fractional exponents.
For example, the cubed root of 3 is expressed as \( \sqrt[3]{3} \) or \( 3^{\frac{1}{3}} \).
Mathematical Representation
Mathematically, if \( x \) is the cubed root of \( y \), then:
\[ x = \sqrt[3]{y} \quad \text{or} \quad x = y^{\frac{1}{3}} \]
Calculating the Cubed Root
To calculate the cubed root of a number, follow these steps:
- Identify the number for which you need to find the cubed root (in this case, 3).
- Use a calculator or mathematical software to compute the cubed root, or use estimation techniques for a rough value.
- Verify the result by cubing the value obtained and checking if it equals the original number.
Properties of Cubed Roots
- Unique Real Value: Every real number has one unique real cubed root.
- Sign Preservation: The cubed root of a positive number is positive, and the cubed root of a negative number is negative.
- Zero: The cubed root of zero is zero.
Visual Representation
Consider a cube with a volume of 27 cubic units. Each side of the cube will be the cubed root of 27, which is 3:
| Volume | Side Length |
| 27 cubic units | 3 units |
Similarly, the cubed root of 3 would be the side length of a cube with a volume of 3 cubic units, approximately \( 1.442 \) units:
| Volume | Side Length |
| 3 cubic units | \( \sqrt[3]{3} \approx 1.442 \) units |
Understanding the Cubed Root of 3
The cubed root of a number is the value that, when multiplied by itself three times, gives the original number. Mathematically, the cube root of a number \(a\) is denoted as \(\sqrt[3]{a}\), and it satisfies the equation:
\[b^3 = a\]
For the cubed root of 3, this means finding a number \(b\) such that:
\[b^3 = 3\]
Using approximation methods, we can determine that the cubed root of 3 is an irrational number, approximately equal to 1.442249. This means:
\[\sqrt[3]{3} \approx 1.442249\]
To manually approximate the cube root of 3, you can use iterative methods. Start with a close guess, such as 1.4, and refine it:
- Divide 3 by your initial guess: \( \frac{3}{1.4} \approx 2.1428 \)
- Average the result with your guess: \( \frac{1.4 + 1.4 + 2.1428}{3} \approx 1.6476 \)
- Refine further by repeating the process with the new average.
After a few iterations, you will converge to the value of approximately 1.442249.
Understanding the cube root of 3 is not only important for mathematical problems but also has practical applications in geometry, physics, and engineering where the relationships between volume and linear dimensions are crucial.
In summary, the cube root of 3 is an irrational number approximately equal to 1.442249, and it plays a significant role in various mathematical and real-world applications.
Approximate Value and Calculation Methods
The cubed root of 3, represented as or ∛3, is an irrational number. This means it cannot be expressed as a simple fraction. Its approximate value is:
Calculation Methods
1. Estimation and Refinement
One way to approximate the cubed root of 3 is by estimation and refinement. Here's a step-by-step method:
- Start with an initial guess. For ∛3, we can start with 1.4.
- Refine the guess using the formula:
- Perform the calculation to refine the estimate. For example:
- The refined estimate is approximately 1.442.
2. Using Halley's Method
Another method is Halley's method, which uses a formula for iterative refinement:
For a = 3 and an initial guess x = 1:
The result is approximately 1.442.
3. Prime Factorization
The prime factorization method involves finding the prime factors and grouping them:
- Find the prime factors of 3:
- Since 3 is already prime, the simplest form is:
This method confirms that ∛3 is approximately 1.442.
Using Calculators and Software
Calculating the cubed root of 3 can be done efficiently using various calculators and software tools. Here are the steps and methods to perform this calculation:
Using a Scientific Calculator
- Turn on your scientific calculator.
- Enter the number
3. - Press the
[∛]button, which is specifically designed for calculating cube roots. - The display will show the cubed root of 3, which is approximately 1.4422495703074.
Using Spreadsheet Software (Excel, Google Sheets, Numbers)
To calculate the cubed root of 3 using spreadsheet software, you can use the power function.
- Open your spreadsheet application (Excel, Google Sheets, Numbers).
- Select a cell and enter the formula:
=3^(1/3). - Press
Enter, and the cell will display the cubed root of 3, approximately 1.4422495703074.
Using Online Calculators
Online calculators provide a convenient way to find the cubed root of 3. Here’s how to use them:
- Go to an online calculator website.
- Enter the number
3in the input field. - Press the button for calculating the cubed root, usually labeled
[∛]or similar. - The result, approximately 1.4422495703074, will be displayed on the screen.
Using Programming Languages
You can also calculate the cubed root of 3 using programming languages like Python. Here’s an example in Python:
import math
cubed_root_of_3 = math.pow(3, 1/3)
print(cubed_root_of_3)
This script will output the cubed root of 3, approximately 1.4422495703074.
By using these methods, you can easily and accurately calculate the cubed root of 3 using various tools and software.
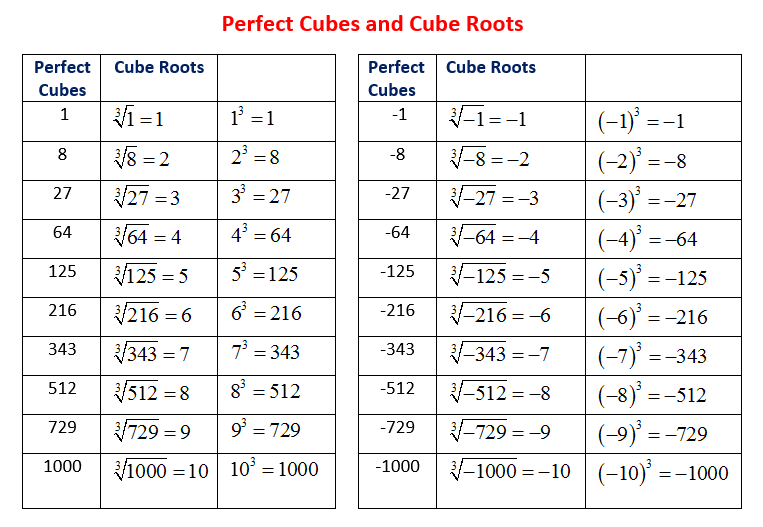
Manual Calculation Techniques
Calculating the cube root of a number manually involves several techniques. Here, we will explore the prime factorization method and the estimation method.
Prime Factorization Method
This method involves breaking down the number into its prime factors and then grouping them to find the cube root.
- Find the prime factors of the given number.
- Express the number as the product of its prime factors.
- Group the factors into sets of three identical factors.
- Take one factor from each set and multiply them together to get the cube root.
For example, to find the cube root of \(216\):
\(216 = 2 \times 2 \times 2 \times 3 \times 3 \times 3\)
Group the factors: \((2 \times 2 \times 2) \) and \((3 \times 3 \times 3)\)
Take one factor from each group: \(2 \times 3 = 6\)
Thus, \(\sqrt[3]{216} = 6\)
Estimation Method
This method is useful for quickly finding an approximate value of the cube root.
- Find the nearest perfect cubes that the given number lies between.
- Estimate where the number falls between these perfect cubes.
- Adjust your estimate accordingly.
For instance, to estimate the cube root of \(50\):
The nearest perfect cubes are \(27\) (\(3^3\)) and \(64\) (\(4^3\)).
Since \(50\) is closer to \(27\) than \(64\), the cube root of \(50\) is slightly less than \(3\).
Long Division Method
This method is more precise and involves a process similar to long division:
- Group the digits of the number in sets of three, starting from the decimal point.
- Estimate the largest number whose cube is less than or equal to the first group.
- Subtract the cube of this number from the first group and bring down the next set of three digits.
- Form a new divisor using the formula \(3a^2 + 3ab + b^2\), where \(a\) is the previous quotient and \(b\) is the new digit.
- Continue the process until the desired precision is achieved.
For example, to find the cube root of \(55,742,968\):
Start with \(38\) (since \(38^3 = 54,872,000\) is close to \(55,742,968\)).
Using long division steps, refine the digits step by step to get \(382\).
Applications of the Cubed Root of 3
The cubed root of 3, represented as \(\sqrt[3]{3}\), finds application in various fields of mathematics, science, and engineering. Here are some key areas where this mathematical concept is utilized:
-
Geometry:
In geometry, the cubed root of 3 is used to determine the dimensions of cubes and other three-dimensional shapes. For example, if the volume of a cube is known, the cubed root helps in finding the side length of the cube.
-
Engineering:
Engineers use the cubed root of 3 in calculations involving materials and structures. For instance, when designing objects with cubic symmetry or analyzing stresses and strains in materials, this root is essential for precise computations.
-
Physics:
In physics, the cubed root of 3 appears in equations related to wave functions, quantum mechanics, and other areas where cubic equations are involved. It helps in solving problems that describe physical phenomena with cubic relationships.
-
Algebra:
The cubed root of 3 is frequently used in algebra to solve cubic equations. These equations are common in various algebraic problems and require finding the roots for accurate solutions.
-
Data Analysis:
In data analysis, particularly in transforming data distributions, the cubed root can be used to normalize skewed data. This helps in achieving a more symmetrical distribution, facilitating better statistical analysis.
-
Cryptography:
Certain cryptographic algorithms incorporate the cubed root function to enhance security. These algorithms rely on the mathematical properties of cube roots to create complex keys that are difficult to decipher.
-
Finance:
In finance, the cubed root of 3 may be used in models that predict economic growth or in the analysis of compound interest where growth rates are considered over time.
Overall, the cubed root of 3 is a versatile mathematical tool with applications that extend across various disciplines, highlighting its importance in both theoretical and practical contexts.
Geometric Interpretations
Understanding the geometric interpretation of the cubed root of 3 can provide deeper insights into its properties and applications. Geometrically, the cubed root of a number is often visualized in relation to volumes and three-dimensional shapes.
For instance, consider a cube with a volume of 3 cubic units. The side length of this cube is the cubed root of 3, denoted as \( \sqrt[3]{3} \). This means that if each side of the cube measures \( \sqrt[3]{3} \) units, the volume of the cube will be exactly 3 cubic units. This can be represented mathematically as:
\[
\text{Volume} = (\sqrt[3]{3})^3 = 3
\]
Another way to understand the cubed root geometrically is through the concept of scaling. If you scale a cube such that its side length is increased to \( \sqrt[3]{3} \) times its original side length, its volume will scale up to 3 times its original volume.
Furthermore, the geometric interpretation can also extend to higher dimensions and complex numbers. When dealing with complex roots, the cube roots of a number are represented as points in the complex plane, equidistant from the origin and spaced evenly around a circle. For the cubed root of 3, the principal (real) root is of primary interest, and it can be visualized on the real number line.
Visual tools and geometric constructions, such as drawing a cube and measuring its side lengths, help in grasping the concept of the cubed root of 3 in a tangible manner. Using these interpretations, one can better understand not only the abstract numerical value but also its practical and spatial significance.
Physics and Engineering Applications
The cubed root of 3 (\(\sqrt[3]{3}\)) plays a significant role in various physics and engineering applications. Understanding its applications can help in solving complex problems related to these fields.
- Volume Calculations: In physics and engineering, the cubed root is often used to determine the dimensions of a cube when the volume is known. For example, if the volume of a cube is 27 cubic units, the side length of the cube can be found using the cubed root of 27, which is 3. This is essential in material science and manufacturing processes where precise measurements are critical.
- Resonance Frequencies: In mechanical and electrical engineering, the natural frequencies of vibrating systems or electrical circuits can be related to the cube roots of certain parameters. For instance, the resonance frequency of a mechanical structure or an electrical LC circuit might involve the cube root of mass or inductance values, which helps in designing stable and efficient systems.
- Quantum Mechanics: The cubed root of 3 appears in the normalization of wave functions in quantum mechanics. Specifically, in the study of atomic orbitals and the behavior of particles in a potential well, the expectation values of certain operators involve cube roots, aiding in the precise calculation of energy levels and probabilities.
- Material Properties: Engineering applications often require understanding the material properties like density and strength, which can be related to their volume. Using the cubed root helps in scaling these properties accurately when designing components and structures.
- Fluid Dynamics: In fluid dynamics, the cubed root is used to describe the scaling laws of turbulent flows and mixing processes. For instance, the size of eddies in a turbulent flow can be related to the cube root of the energy dissipation rate, which is crucial for predicting and controlling flow behavior in pipelines and reactors.
These applications show that the cubed root of 3 is not just a mathematical curiosity but a practical tool in various scientific and engineering disciplines.

Algebraic Equations Involving Cubic Roots
The cubed root of a number is a value that, when multiplied by itself three times, yields the original number. For instance, the cubed root of 3, denoted as ∛3, is approximately 1.442.
In algebra, cubic roots are often used to solve equations involving cubic terms. Here are some examples and methods:
Example 1: Solving Basic Cubic Equations
Consider the equation:
\[ x^3 = 3 \]
To solve for \( x \), we take the cubed root of both sides:
\[ x = \sqrt[3]{3} \approx 1.442 \]
Example 2: Cubic Roots in Polynomial Equations
For a more complex equation such as:
\[ x^3 + 3x^2 - 2 = 0 \]
We might need to factor or use numerical methods to find the roots. However, recognizing that any real root will involve finding the cubic root of a simplified form can help in approximating solutions.
Solving Systems of Equations
Sometimes, cubic roots appear in systems of equations. Consider the system:
- \[ y = \sqrt[3]{x} \]
- \[ x + y = 4 \]
Substitute \( y \) in the second equation:
\[ x + \sqrt[3]{x} = 4 \]
This equation can be solved numerically to find the value of \( x \), and consequently \( y \).
Equations with Nested Cubic Roots
Consider an equation with nested cubic roots:
\[ \sqrt[3]{\sqrt[3]{x}} = 1 \]
To solve this, we first understand that if \( \sqrt[3]{\sqrt[3]{x}} = 1 \), then:
\[ \sqrt[3]{x} = 1 \]
So, \( x = 1 \).
Using Cubic Roots in Functions
Functions involving cubic roots can be evaluated for different values of \( x \). For example:
\[ f(x) = 2\sqrt[3]{x} + 5 \]
To find \( f(8) \):
\[ f(8) = 2\sqrt[3]{8} + 5 = 2(2) + 5 = 9 \]
Practice Problems
- Solve \( x^3 - 27 = 0 \).
- Find the real root of \( x^3 + 6x - 20 = 0 \).
- Simplify \( \sqrt[3]{54} + \sqrt[3]{16} \).
These examples illustrate the various ways cubic roots can be used in algebraic equations, from simple isolations to more complex polynomial equations.
Advanced Mathematical Concepts
Understanding the cube root of 3, denoted as \( \sqrt[3]{3} \), opens up a range of advanced mathematical concepts. Below, we explore several areas where the cube root of 3 plays a significant role:
1. Properties of Irrational Numbers
The cube root of 3 is an irrational number, meaning it cannot be expressed as a simple fraction. Its decimal representation is non-repeating and non-terminating, approximately \(1.4422495703074\). This irrational nature influences various mathematical functions and analyses.
2. Polynomial Equations
In algebra, the cube root of 3 can be used to solve polynomial equations of the form \(x^3 = 3\). The solution to this equation is:
\[
x = \sqrt[3]{3}
\]
In general, for a polynomial equation \(x^3 = a\), the solution involves finding the cube root of \(a\).
3. Simplification and Radicals
Simplifying expressions involving cube roots often requires factoring the radicand into its prime components. For instance, simplifying \(\sqrt[3]{27 \times 3}\) involves recognizing that 27 is a perfect cube:
\[
\sqrt[3]{27 \times 3} = \sqrt[3]{27} \times \sqrt[3]{3} = 3\sqrt[3]{3}
\]
4. Complex Numbers
The cube root operation can be extended to complex numbers, leading to multiple solutions. For a complex number \(z\), the cube root is found by solving \(x^3 = z\). This can result in up to three distinct roots, reflecting the nature of complex numbers.
5. Exponential and Logarithmic Relationships
Exponential and logarithmic functions often utilize cube roots. For example, the natural logarithm of \( \sqrt[3]{3} \) is:
\[
\ln(\sqrt[3]{3}) = \frac{1}{3}\ln(3)
\]
6. Applications in Higher Mathematics
Cube roots are integral in solving differential equations, particularly those involving cubic polynomials. They are also used in certain integration techniques and in the study of power series.
7. Practical Applications
Beyond theoretical mathematics, the cube root of 3 has practical applications in fields like physics and engineering, where it is used in volume calculations and scaling laws.
8. Numerical Methods
Approximating cube roots using numerical methods such as Newton's method or iterative algorithms is a crucial part of computational mathematics.
Conclusion
The cube root of 3, while seemingly a simple concept, touches upon numerous advanced mathematical principles and applications, highlighting the interconnectedness of mathematical theories.
Real-World Examples
The cubed root of 3 has various real-world applications, particularly in fields that involve three-dimensional measurements and computations. Understanding how to work with cubic roots is essential for solving practical problems in geometry, engineering, and other sciences.
-
Calculating Dimensions of a Three-Dimensional Object
When the volume of an object is known, its dimensions can be determined by calculating the cube root of the volume. For example, if a cubic container has a volume of 27 cubic units, the length of each side is the cube root of 27, which is 3 units.
This principle helps in various industries, such as construction, where knowing the dimensions from volume measurements is crucial for planning materials and space.
-
Determining Material Quantities
Engineers and builders often use the cube root to estimate the amount of materials required for constructing cubic structures. For example, if an engineer needs to fill a cubic tank with a volume of 125 cubic meters, the cube root of 125 (which is 5) provides the length of each side of the tank, helping to determine the material needed for construction.
-
Volume of Containers
Many containers, such as ice cream boxes or water tanks, have cubic shapes. To find out how much they can hold, the cube root of the volume is calculated. For instance, if a milk crate has a volume of 64 cubic liters, the side length of the crate is 4 liters (the cube root of 64), which helps in planning storage and transportation logistics.
-
Architectural Design
Architects use the concept of cubic roots in designing and scaling models of buildings. By knowing the volume and using the cube root, they can accurately scale the dimensions of a structure to create models that are proportionate and true to the intended design.
-
Engineering Applications
In engineering, particularly in materials science, cube roots are used to calculate properties related to strength and density. For example, the tensile strength of a cubic block of material can be enhanced by precise calculations of its dimensions using cubic roots.
Understanding the cubed root of a number like 3 is fundamental in these applications, ensuring accuracy and efficiency in both theoretical and practical scenarios.
Visual Representations
Visualizing the cube root of 3 can help in understanding its properties and applications better. Below are several methods and examples of visual representations:
Graphical Representation
One effective way to visualize the cube root of 3 is by plotting it on a graph. Using graphing calculators like Desmos, you can plot the function \( y = \sqrt[3]{x} \). When \( x = 3 \), the value of \( y \) will be approximately 1.442.
Here's a simple graph to illustrate:
Geometric Representation
Geometrically, the cube root of a number represents the side length of a cube whose volume equals the given number. For instance, if you have a cube with a volume of 3 cubic units, each side of the cube will be \( \sqrt[3]{3} \) units long.
- Volume of the cube: \( V = 3 \) cubic units
- Side length of the cube: \( s = \sqrt[3]{3} \approx 1.442 \) units
Numerical Representation
To understand the cube root of 3 numerically, consider its decimal approximation. The cube root of 3 is approximately 1.4422495703074. This value can be rounded to various decimal places for simplicity:
- To the nearest tenth: 1.4
- To the nearest hundredth: 1.44
- To the nearest thousandth: 1.442
Algebraic Representation
The cube root of 3 can also be represented algebraically. If \( x = \sqrt[3]{3} \), then \( x^3 = 3 \). This relationship is useful in solving equations involving cubic roots.
Interactive Representation
Using online tools like the Desmos graphing calculator, you can interactively explore the cube root function by adjusting the input values and observing the changes in the output. This dynamic approach helps in gaining a deeper understanding of the behavior of the cube root function.
Visualizing Applications
The cube root of 3 has practical applications in various fields, such as engineering, physics, and computer graphics. For example, in 3D modeling, understanding the cube root helps in determining dimensions for objects based on volume constraints.
Conclusion
Visual representations of the cube root of 3, whether through graphs, geometric models, or numerical approximations, provide a comprehensive understanding of its properties and applications. Utilizing tools like graphing calculators can enhance this understanding through interactive exploration.

Common Mistakes and Misconceptions
When dealing with the cube root of 3, there are several common mistakes and misconceptions that students and even professionals might encounter. Understanding these errors can help in avoiding them and ensuring accurate calculations.
Mistake 1: Incorrect Decimal Approximation
One common mistake is approximating the cube root of 3 incorrectly. The cube root of 3 is approximately 1.4422495703074. Rounding this number too early or too inaccurately can lead to significant errors in calculations.
- Incorrect: \( \sqrt[3]{3} \approx 1.4 \)
- Correct: \( \sqrt[3]{3} \approx 1.442 \) (to three decimal places)
Mistake 2: Confusing Square Root and Cube Root
Another common error is confusing the square root with the cube root. The square root of 3 is different from the cube root of 3:
- \( \sqrt{3} \approx 1.732 \)
- \( \sqrt[3]{3} \approx 1.442 \)
Mistake 3: Misunderstanding the Concept of Roots
Some students might misunderstand the concept of roots, thinking that all roots (square, cube, etc.) work the same way. It's essential to understand that the cube root involves finding a number that, when multiplied by itself three times, equals the original number.
\( x = \sqrt[3]{3} \implies x^3 = 3 \)
Mistake 4: Ignoring Negative Roots
When solving cubic equations, it’s important to consider both positive and negative roots. For example, the equation \( x^3 = -3 \) has a solution of \( x = -\sqrt[3]{3} \), which is approximately -1.442.
Mistake 5: Incorrect Use in Equations
Errors often occur when incorporating cube roots into algebraic equations. For example, solving \( x^3 + 3 = 0 \) should correctly include the step:
\[
x^3 = -3 \implies x = \sqrt[3]{-3} \approx -1.442
\]
Misconception 1: Cube Root of a Negative Number
A common misconception is that the cube root of a negative number does not exist. In reality, the cube root of a negative number is negative. For example:
\[
\sqrt[3]{-3} \approx -1.442
\]
Misconception 2: Only One Cube Root
Another misconception is that there is only one cube root for any given number. While there is one real cube root, complex numbers also provide two additional cube roots. However, in real number calculations, we typically consider only the real root.
Misconception 3: Simplifying Expressions Incorrectly
Sometimes, students incorrectly simplify expressions involving cube roots. For example, assuming \( \sqrt[3]{a \times b} = \sqrt[3]{a} \times \sqrt[3]{b} \) is correct, but it requires careful application:
\[
\sqrt[3]{27 \times 3} = \sqrt[3]{81} \neq \sqrt[3]{27} \times \sqrt[3]{3} \implies 3\sqrt[3]{3} = 3 \times 1.442 = 4.326
\]
Conclusion
By being aware of these common mistakes and misconceptions, students can improve their understanding and handling of cube roots, leading to more accurate and confident mathematical problem-solving.
Practice Problems and Solutions
Practicing cube roots helps solidify understanding of the concept. Here are some practice problems involving the cubed root of 3, along with their solutions:
-
Find the cube root of 27.
Solution:
- 27 is a perfect cube since \(27 = 3^3\).
- Therefore, \( \sqrt[3]{27} = 3\).
-
Solve for \(x\) in the equation \(x^3 = 27\).
Solution:
- Taking the cube root of both sides: \(x = \sqrt[3]{27}\).
- We know \( \sqrt[3]{27} = 3\), hence \( x = 3 \).
-
Find the cube root of 8/27.
Solution:
- First, express the fraction as \(\frac{8}{27} = \frac{2^3}{3^3}\).
- The cube root of the fraction is \(\sqrt[3]{\frac{8}{27}} = \frac{\sqrt[3]{8}}{\sqrt[3]{27}}\).
- This simplifies to \(\frac{2}{3}\), as \( \sqrt[3]{8} = 2 \) and \( \sqrt[3]{27} = 3 \).
- Therefore, \( \sqrt[3]{\frac{8}{27}} = \frac{2}{3}\).
-
Check if 2 is the cube root of 8.
Solution:
- Calculate \(2^3 = 2 \times 2 \times 2 = 8\).
- Since \( 2^3 = 8 \), \(2\) is indeed the cube root of \(8\).
-
What is the cube root of 64?
Solution:
- Express 64 as a product of primes: \(64 = 2^6\).
- The cube root of \(2^6\) is \( \sqrt[3]{2^6} = 2^2 \times 2^2 = 2^2\).
- Thus, \( \sqrt[3]{64} = 4\).
These practice problems illustrate various approaches to understanding and working with cube roots, including solving equations, verifying cube roots, and simplifying fractional cube roots.
Summary and Conclusion
The cubed root of 3, denoted as , is an irrational number approximately equal to 1.442. It is the number which, when multiplied by itself three times, results in 3.
The cubed root of 3 is significant in various mathematical and real-world applications. It plays a crucial role in solving cubic equations, understanding geometric properties, and is used in fields such as physics and engineering.
Calculating the cubed root of 3 can be done using several methods, including prime factorization, approximation techniques, and using calculators or software. Manual calculation methods offer insight into the number's properties and applications, although using calculators or software provides quick and accurate results.
Common mistakes in dealing with cubed roots include confusing them with square roots or misinterpreting their values in calculations. Proper understanding and practice can help in avoiding these errors.
Overall, the cubed root of 3 is a fascinating number with diverse applications. A clear understanding of its properties and computation methods enhances mathematical proficiency and its practical application in various fields.
Video Giới thiệu về Căn bậc ba với Thầy J cung cấp một cách hiểu đơn giản và rõ ràng về khái niệm căn bậc ba.
Giới thiệu về Căn bậc ba | Toán học với Thầy J
READ MORE:
Video giải đáp câu hỏi phỏng vấn Cambridge: Xác định số lớn hơn giữa căn bậc hai của 2 và căn bậc ba của 3.
Câu Hỏi Phỏng Vấn Cambridge! Xác Định Số Lớn Hơn? Căn Bậc Hai của 2 hay Căn Bậc Ba của 3