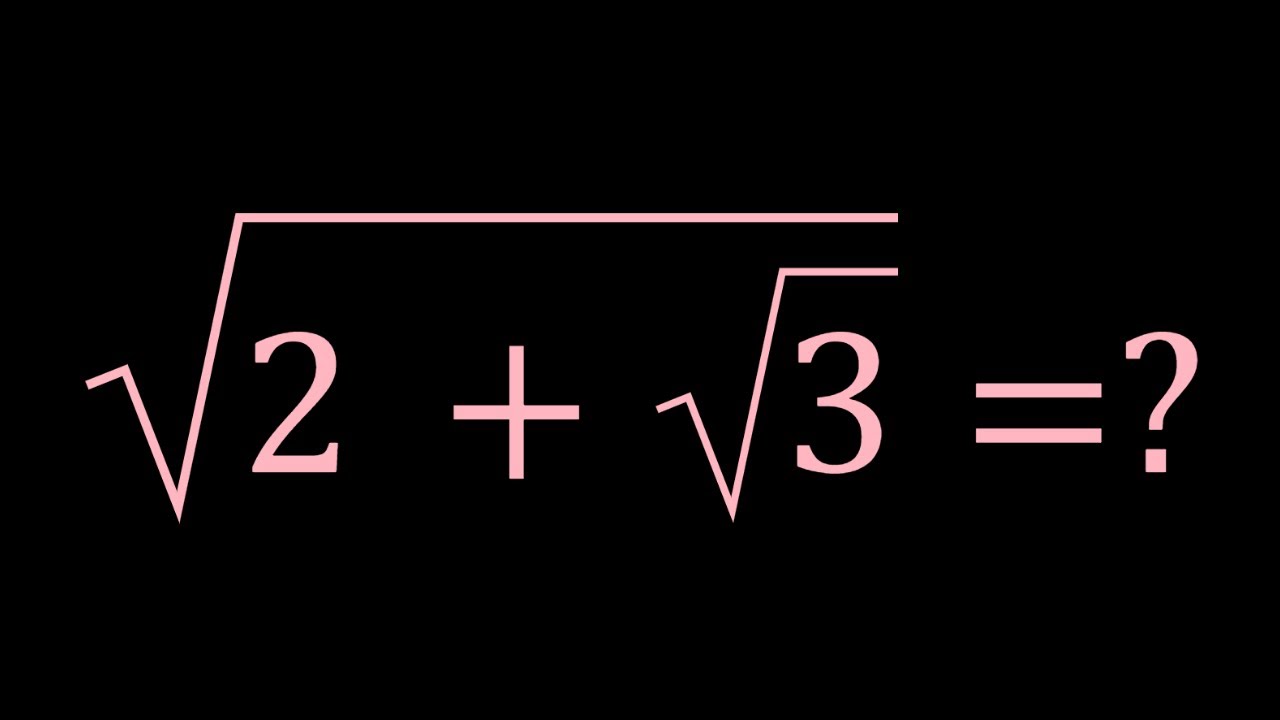Topic square root of 3 plus square root of 3: The expression "square root of 3 plus square root of 3" might seem complex at first, but it simplifies elegantly. In this article, we explore the step-by-step process of simplifying this expression, its mathematical significance, and practical applications, making it easy for anyone to understand and apply in various contexts.
Table of Content
- Understanding the Sum of Square Roots
- Introduction to Square Roots
- Basic Arithmetic with Square Roots
- Simplifying Square Root Expressions
- Understanding \(\sqrt{3} + \sqrt{3}\)
- Step-by-Step Simplification Process
- Practical Applications in Mathematics
- Common Mistakes to Avoid
- Advanced Concepts Related to Square Roots
- Frequently Asked Questions
- Conclusion
- YOUTUBE: Video này giải thích cách cộng hai căn bậc hai, cụ thể là sqrt(3) + sqrt(27). Hãy cùng tìm hiểu cách đơn giản hóa biểu thức này và áp dụng nó trong toán học.
Understanding the Sum of Square Roots
When we add the square root of 3 to itself, we can express it mathematically as:
\[ \sqrt{3} + \sqrt{3} \]
This simplifies to:
\[ 2\sqrt{3} \]
Here’s a detailed breakdown:
- The square root of 3 (\( \sqrt{3} \)) is an irrational number approximately equal to 1.732.
- When you add \( \sqrt{3} \) to another \( \sqrt{3} \), you essentially have two of them.
- This is similar to adding any number to itself, like 1 + 1 = 2 or x + x = 2x.
Steps to Simplify:
- Start with the expression \( \sqrt{3} + \sqrt{3} \).
- Recognize that adding identical terms is the same as multiplying by 2.
- Thus, \( \sqrt{3} + \sqrt{3} = 2\sqrt{3} \).
Therefore, the simplified form of \( \sqrt{3} + \sqrt{3} \) is:
\[ 2\sqrt{3} \]
This result can be useful in various mathematical contexts, including solving equations and simplifying expressions.

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics. A square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 9 is 3, because \( 3 \times 3 = 9 \).
Let's break down the basics:
- A square root is represented by the radical symbol \( \sqrt{} \).
- For any non-negative number \( x \), the square root of \( x \) is written as \( \sqrt{x} \).
- Square roots can be perfect (such as \( \sqrt{4} = 2 \)) or irrational (such as \( \sqrt{3} \approx 1.732 \)).
Square roots are used in various mathematical contexts, including solving equations, geometry, and real-world applications. Understanding how to simplify and manipulate square roots is essential for mastering more advanced mathematical concepts.
For example, when dealing with the expression \( \sqrt{3} + \sqrt{3} \), it is crucial to recognize that it can be simplified by factoring out common terms:
\[ \sqrt{3} + \sqrt{3} = 2\sqrt{3} \]
This simplification shows that adding two identical square roots is akin to multiplying the square root by 2.
Let's delve deeper into simplifying square root expressions and understanding their properties.
Basic Arithmetic with Square Roots
Understanding basic arithmetic operations with square roots is essential for solving more complex mathematical problems. Let's explore the key operations step by step:
Addition and Subtraction
To add or subtract square roots, they must be like terms, meaning they have the same radicand (the number under the square root symbol).
- Example: \( \sqrt{3} + \sqrt{3} = 2\sqrt{3} \)
- If the radicands are different, the terms cannot be combined:
\( \sqrt{2} + \sqrt{3} \neq \sqrt{5} \)
Multiplication
Multiplying square roots is straightforward. Multiply the numbers under the square roots, and then take the square root of the product.
- Example:
\( \sqrt{2} \times \sqrt{3} = \sqrt{2 \times 3} = \sqrt{6} \)
Division
Dividing square roots involves dividing the numbers under the square roots and then taking the square root of the quotient.
- Example:
\( \frac{\sqrt{8}}{\sqrt{2}} = \sqrt{\frac{8}{2}} = \sqrt{4} = 2 \)
Rationalizing the Denominator
When a square root appears in the denominator, it is often useful to rationalize the denominator. This means converting the expression so that the denominator is a rational number.
- Multiply the numerator and the denominator by the square root in the denominator.
- Example:
\( \frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3} \)
Simplification of Square Roots
Square roots can often be simplified by factoring out perfect squares.
- Example:
\( \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3} \)
Mastering these basic arithmetic operations with square roots provides a strong foundation for solving more complex problems and understanding advanced mathematical concepts.
Simplifying Square Root Expressions
Simplifying square root expressions involves reducing the expression to its simplest form. This often includes combining like terms, factoring, and rationalizing. Here are the detailed steps:
Combining Like Terms
Like terms in square root expressions have the same radicand. They can be combined by adding or subtracting their coefficients.
- Example:
\( \sqrt{3} + \sqrt{3} = 2\sqrt{3} \)
- If the radicands are different, the terms cannot be combined:
\( \sqrt{2} + \sqrt{3} \neq \sqrt{5} \)
Factoring Inside the Square Root
To simplify square roots, factor the number inside the square root into its prime factors and look for perfect squares.
- Example:
\( \sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2} \)
Simplifying Nested Square Roots
When dealing with nested square roots, simplify the inner square root first.
- Example:
\( \sqrt{4 + \sqrt{4}} = \sqrt{4 + 2} = \sqrt{6} \)
Rationalizing the Denominator
To remove square roots from the denominator, multiply both the numerator and the denominator by the square root in the denominator.
- Identify the square root in the denominator.
- Multiply the numerator and the denominator by this square root.
- Example:
\( \frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3} \)
Using Conjugates to Simplify Expressions
For expressions with square roots in the denominator, multiply by the conjugate to simplify.
- The conjugate of \( a + \sqrt{b} \) is \( a - \sqrt{b} \).
- Example:
\( \frac{1}{1 + \sqrt{3}} \times \frac{1 - \sqrt{3}}{1 - \sqrt{3}} = \frac{1 - \sqrt{3}}{1 - 3} = \frac{1 - \sqrt{3}}{-2} = -\frac{1 - \sqrt{3}}{2} \)
By following these steps, you can simplify complex square root expressions into more manageable forms, making calculations easier and more intuitive.
Understanding \(\sqrt{3} + \sqrt{3}\)
The expression \(\sqrt{3} + \sqrt{3}\) involves adding two identical square roots. This might initially appear complex, but it simplifies quite elegantly. Here’s a detailed breakdown of how to understand and simplify this expression:
Step-by-Step Simplification
- Recognize that you are adding two like terms:
\(\sqrt{3}\) and \(\sqrt{3}\) are like terms because they have the same radicand (3).
- Combine the coefficients of the like terms:
- The coefficient of the first \(\sqrt{3}\) is 1.
- The coefficient of the second \(\sqrt{3}\) is also 1.
- Add the coefficients together:
\(1 + 1 = 2\)
- Attach the common square root to the sum of the coefficients:
\(\sqrt{3} + \sqrt{3} = 2\sqrt{3}\)
Visualizing the Simplification
To further understand, visualize the process as grouping identical objects:
- Imagine you have one \(\sqrt{3}\) apple and another \(\sqrt{3}\) apple.
- Combining these gives you two \(\sqrt{3}\) apples, or \(2\sqrt{3}\).
Mathematical Significance
This simplification shows an important property of square roots and like terms:
- When adding square roots with the same radicand, simply add their coefficients.
- The result is a single term with the combined coefficient and the common square root.
Practical Applications
Understanding how to simplify \(\sqrt{3} + \sqrt{3}\) is useful in various mathematical contexts, such as:
- Simplifying expressions in algebra and calculus.
- Solving equations involving square roots.
- Applying in geometry and trigonometry problems where roots are involved.
By mastering this fundamental concept, you can tackle more complex problems with confidence and ease.

Step-by-Step Simplification Process
The expression \(\sqrt{3} + \sqrt{3}\) may seem intricate at first glance, but it can be simplified straightforwardly. Here is the detailed, step-by-step process to simplify this expression:
Identifying Like Terms
The first step in simplifying \(\sqrt{3} + \sqrt{3}\) is to recognize that both terms are like terms since they have the same radicand (3).
Adding Coefficients
- Each \(\sqrt{3}\) has an implicit coefficient of 1:
- The first term: \(1\sqrt{3}\)
- The second term: \(1\sqrt{3}\)
- Add the coefficients together:
\(1 + 1 = 2\)
Forming the Simplified Expression
After adding the coefficients, attach the common square root to the sum of the coefficients:
\(\sqrt{3} + \sqrt{3} = 2\sqrt{3}\)
Detailed Example
| Original Expression | \(\sqrt{3} + \sqrt{3}\) |
| Step 1: Identify coefficients | \(1\sqrt{3} + 1\sqrt{3}\) |
| Step 2: Add coefficients | \(1 + 1 = 2\) |
| Step 3: Combine with common square root | \(2\sqrt{3}\) |
Visual Representation
Visualizing the process can make it clearer:
- Think of \(\sqrt{3}\) as a single unit (like an apple).
- Having \(\sqrt{3} + \sqrt{3}\) is like having one apple plus one apple.
- Combining them gives you two apples, or \(2\sqrt{3}\).
Conclusion
By following these steps, you can simplify \(\sqrt{3} + \sqrt{3}\) to \(2\sqrt{3}\) effortlessly. This method can be applied to any similar expressions involving square roots, helping to simplify and solve complex mathematical problems.
Practical Applications in Mathematics
The expression \(\sqrt{3} + \sqrt{3} = 2\sqrt{3}\) has numerous practical applications in various fields of mathematics. Understanding how to manipulate and simplify such expressions is crucial for solving a wide range of mathematical problems. Here are some key areas where this knowledge is applied:
Algebra
In algebra, simplifying expressions involving square roots is essential for solving equations and inequalities. For instance:
- Simplifying Polynomials:
Expressions like \(\sqrt{3}x + \sqrt{3}y\) can be simplified to \(2\sqrt{3}(x + y)\), making it easier to solve for variables.
- Solving Quadratic Equations:
When solving quadratic equations, roots often appear, and simplifying them can lead to more straightforward solutions.
Geometry
Square roots frequently appear in geometric formulas, especially when dealing with right triangles, circles, and other shapes:
- Right Triangles:
In the context of the Pythagorean theorem, \(\sqrt{3}\) appears as a result of calculations involving the sides of a triangle.
- Areas and Volumes:
Simplifying square roots can help in calculating areas and volumes, such as finding the height of an equilateral triangle where the height is \(\sqrt{3}/2\) times the side length.
Trigonometry
In trigonometry, square roots are common in the values of trigonometric functions:
- Special Angles:
Angles like 30°, 45°, and 60° have sine, cosine, and tangent values that include \(\sqrt{3}\). Simplifying expressions involving these angles is crucial for solving trigonometric equations.
- Trigonometric Identities:
Identities such as the double-angle formulas often involve square roots, and simplifying these expressions helps in verifying and using these identities.
Calculus
Simplifying square roots is vital in calculus, especially when dealing with limits, derivatives, and integrals:
- Limits:
Simplifying square roots in limit problems can make it easier to find the limit of a function as it approaches a particular value.
- Derivatives and Integrals:
Square roots often appear in the process of finding derivatives and integrals. Simplifying these expressions can streamline calculations and lead to more accurate results.
Physics and Engineering
In physics and engineering, square roots are used in various formulas and calculations:
- Kinematics:
Equations involving motion, such as those calculating distance or speed, often include square roots.
- Wave Mechanics:
Square roots appear in formulas describing wave speed and frequencies.
By mastering the simplification of expressions like \(\sqrt{3} + \sqrt{3} = 2\sqrt{3}\), students and professionals can solve a wide range of problems more efficiently and accurately, reinforcing the importance of this fundamental mathematical skill.
Common Mistakes to Avoid
When working with the expression \(\sqrt{3} + \sqrt{3}\), it's easy to make mistakes that can lead to incorrect results. Below are some common errors and how to avoid them:
-
Incorrect Addition of Square Roots:
A common mistake is to add the square roots directly as if they were like terms. For example, \(\sqrt{3} + \sqrt{3} \neq \sqrt{6}\). Instead, remember that \(\sqrt{3} + \sqrt{3} = 2\sqrt{3}\).
-
Forgetting to Simplify Completely:
Sometimes, the process of simplifying square root expressions is not carried out fully. For instance, \(\sqrt{3} + \sqrt{3}\) should be simplified to \(2\sqrt{3}\), not left in its original form.
-
Confusing Multiplication with Addition:
Another error is confusing the operations of addition and multiplication of square roots. While \(\sqrt{3} + \sqrt{3} = 2\sqrt{3}\), the expression \(\sqrt{3} \times \sqrt{3} = 3\), since multiplying two square roots results in the radicand.
-
Incorrectly Assuming the Radicands Must be Combined:
Do not assume that the radicands (the numbers inside the square roots) can be combined. For example, \(\sqrt{3} + \sqrt{3}\) does not equal \(\sqrt{3 + 3}\). Each term should be simplified individually and then combined.
-
Ignoring the Properties of Square Roots:
Remember the fundamental properties of square roots, such as \(\sqrt{a} \times \sqrt{b} = \sqrt{ab}\) and \((\sqrt{a})^2 = a\). Misapplying these properties can lead to incorrect results.
Advanced Concepts Related to Square Roots
Square roots extend beyond basic arithmetic into various advanced mathematical concepts. Here are some advanced topics related to square roots:
-
Complex Numbers and Square Roots:
When dealing with negative numbers under the square root, we introduce complex numbers. The imaginary unit \(i\) is defined as \(i = \sqrt{-1}\). Thus, for any negative number \(-a\), the square root is \(\sqrt{-a} = i\sqrt{a}\). For example, \(\sqrt{-9} = 3i\).
-
Irrational Square Roots:
Square roots of non-perfect squares are irrational numbers. These numbers cannot be expressed as a simple fraction and their decimal form goes on forever without repeating. For instance, \(\sqrt{2}\) and \(\sqrt{3}\) are irrational.
-
Conjugates and Rationalizing Denominators:
In expressions involving square roots, particularly in fractions, we often rationalize the denominator. This process involves multiplying the numerator and the denominator by the conjugate of the denominator. For example, to rationalize \(\frac{1}{\sqrt{3}}\), we multiply by \(\frac{\sqrt{3}}{\sqrt{3}}\) to get \(\frac{\sqrt{3}}{3}\).
-
Solving Equations with Square Roots:
Equations involving square roots can be solved by isolating the square root term and then squaring both sides of the equation to eliminate the square root. However, it is crucial to check for extraneous solutions that may arise from the squaring process.
-
Properties of Square Roots:
- The product property: \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- The quotient property: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- These properties are useful in simplifying complex radical expressions.
-
Square Root Functions:
The square root function \(f(x) = \sqrt{x}\) is a fundamental function in mathematics. It is defined for all non-negative \(x\) and produces non-negative outputs. The graph of \(f(x)\) is a curve that starts at the origin (0,0) and increases gradually.
Understanding these advanced concepts is essential for higher-level mathematics and their applications in fields such as engineering, physics, and computer science.

Frequently Asked Questions
-
What is \(\sqrt{3} + \sqrt{3}\)?
The expression \(\sqrt{3} + \sqrt{3}\) simplifies to \(2\sqrt{3}\). This is similar to adding like terms in algebra; just as \(x + x = 2x\), \(\sqrt{3} + \sqrt{3} = 2\sqrt{3}\).
-
Can you add square roots of different numbers?
No, you cannot directly add square roots of different numbers. For example, \(\sqrt{3} + \sqrt{5}\) cannot be simplified further because they are not like terms. Each square root term must be simplified individually.
-
How do you simplify the expression \(\sqrt{3} + \sqrt{27}\)?
First, simplify \(\sqrt{27}\):
- Factorize 27: \(27 = 3 \times 3 \times 3\)
- Take the square root of the perfect square: \(\sqrt{27} = \sqrt{3^2 \times 3} = 3\sqrt{3}\)
Thus, \(\sqrt{3} + \sqrt{27} = \sqrt{3} + 3\sqrt{3} = 4\sqrt{3}\).
-
What is the difference between simplifying and adding square roots?
Simplifying square roots involves reducing the square root to its simplest form, often by factoring out perfect squares. Adding square roots involves combining like terms. For instance, \(\sqrt{12}\) simplifies to \(2\sqrt{3}\), but \(\sqrt{3} + \sqrt{5}\) cannot be simplified further as they are unlike terms.
-
How do you handle expressions like \(\sqrt{a} + \sqrt{b}\) in equations?
When solving equations with square roots, isolate the square root term and square both sides to eliminate the square root. For example, to solve \(\sqrt{3x + 5} = 4\), square both sides to get \(3x + 5 = 16\), and then solve for \(x\).
Conclusion
Understanding and working with square roots, such as \(\sqrt{3} + \sqrt{3}\), is a fundamental skill in mathematics that extends beyond basic arithmetic into more advanced concepts. The process of simplifying and combining square roots is straightforward when you recognize that they follow similar rules to algebraic terms. For instance, \(\sqrt{3} + \sqrt{3}\) simplifies to \(2\sqrt{3}\), much like \(x + x = 2x\).
Exploring advanced topics like the manipulation of complex numbers, rationalizing denominators, and solving equations with square roots deepens our comprehension and application of these principles. For example, understanding that \(\sqrt{27}\) simplifies to \(3\sqrt{3}\) allows us to combine it with \(\sqrt{3}\) to get \(4\sqrt{3}\). Such skills are essential in fields that require precise calculations and simplifications, such as engineering, physics, and computer science.
Overall, mastering the basics of square roots provides a strong foundation for tackling more intricate mathematical problems. By avoiding common mistakes, like incorrectly adding unlike radicals or forgetting to fully simplify expressions, you can ensure accuracy in your calculations. Embracing these techniques and concepts will enhance your mathematical proficiency and problem-solving abilities.
Video này giải thích cách cộng hai căn bậc hai, cụ thể là sqrt(3) + sqrt(27). Hãy cùng tìm hiểu cách đơn giản hóa biểu thức này và áp dụng nó trong toán học.
sqrt(3) + sqrt(27), căn bậc hai của 3 + căn bậc hai của 27
READ MORE:
Hướng dẫn cách cộng 2 căn 3 và căn 3. Video này giúp bạn hiểu rõ hơn về phép toán với căn bậc hai.
2 căn 3 + căn 3 || Cách cộng 2 căn 3 và căn 3