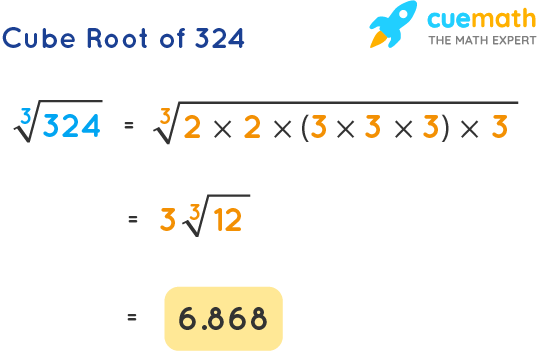
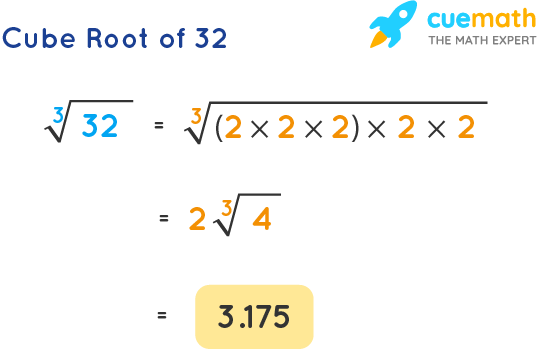
Topic square root of 3 cubed: Discover the intriguing world of mathematics by exploring the square root of 3 cubed. This article delves into the steps to calculate this value, its significance, and its applications in various fields. Join us on this mathematical journey to better understand and appreciate the beauty of numbers.
Table of Content
- Understanding the Square Root of 3 Cubed
- Introduction to Square Roots and Cubes
- Mathematical Foundations
- Calculating the Cube of 3
- Finding the Square Root of 27
- Mathematical Expression and Simplification
- Approximation and Decimal Representation
- Applications in Mathematics and Science
- Practical Examples and Problem Solving
- Advanced Concepts Related to Roots and Powers
- Common Mistakes and How to Avoid Them
- Conclusion and Summary
- YOUTUBE: Khám phá cách tính căn bậc hai và căn bậc ba trong toán học qua video hướng dẫn của Thầy J. Hướng dẫn chi tiết và dễ hiểu giúp bạn nắm vững các khái niệm cơ bản.
Understanding the Square Root of 3 Cubed
In mathematics, finding the square root of a number that is cubed can be broken down into simpler steps.
Step-by-Step Explanation
- First, we find the cube of 3:
- Next, we find the square root of 27:
Mathematical Expression
The expression can be written as:
This means that the square root of 3 cubed is approximately 5.196.
Conclusion
Understanding the square root of a cubed number involves first cubing the number and then finding the square root of the result. For the number 3, this gives us approximately 5.196.

READ MORE:
Introduction to Square Roots and Cubes
Understanding the concepts of square roots and cubes is fundamental in mathematics. These operations form the basis for more complex calculations and are widely used in various fields, including science, engineering, and finance.
Square Roots
A square root of a number is a value that, when multiplied by itself, gives the original number. For example:
- The square root of 9 is 3, because \(3 \times 3 = 9\).
- The square root of 16 is 4, because \(4 \times 4 = 16\).
In mathematical notation, the square root of a number \(x\) is represented as \(\sqrt{x}\).
Cubes
Cubing a number means multiplying it by itself twice. For instance:
- The cube of 2 is \(2^3 = 2 \times 2 \times 2 = 8\).
- The cube of 3 is \(3^3 = 3 \times 3 \times 3 = 27\).
Combining the Concepts
To find the square root of a cubed number, you follow these steps:
- First, cube the number.
- Then, find the square root of the result.
For example, to find the square root of 3 cubed:
- Cubing 3 gives \(3^3 = 27\).
- Finding the square root of 27 gives \(\sqrt{27} \approx 5.196\).
These basic operations are essential tools in many areas of mathematics and their applications.
Mathematical Foundations
The calculation of the square root of 3 cubed is based on fundamental mathematical concepts involving exponents and roots. Understanding these principles is crucial for accurately performing and comprehending such operations.
Exponents
An exponent indicates how many times a number, known as the base, is multiplied by itself. For example:
- \(3^2\) (3 squared) means \(3 \times 3 = 9\).
- \(3^3\) (3 cubed) means \(3 \times 3 \times 3 = 27\).
Roots
The root of a number is the inverse operation of exponentiation. The square root, in particular, finds a number which, when multiplied by itself, gives the original number. For example:
- \(\sqrt{9} = 3\) because \(3 \times 3 = 9\).
- \(\sqrt{16} = 4\) because \(4 \times 4 = 16\).
Combining Exponents and Roots
When dealing with both exponents and roots, it's helpful to break down the operations step by step. For instance, to find the square root of 3 cubed:
- Cubing the Number: Calculate \(3^3\).
- Finding the Square Root: Calculate \(\sqrt{27}\).
Simplifying the Expression
We can represent the process of finding the square root of 3 cubed in a single mathematical expression:
These steps and principles illustrate the core mathematical foundations necessary to perform and understand the operation of finding the square root of a cubed number.
Calculating the Cube of 3
To calculate the cube of a number means to raise it to the power of three. This operation involves multiplying the number by itself twice. Let's explore the step-by-step process to cube the number 3.
Step-by-Step Calculation
- Start with the Number:
- First Multiplication:
- Second Multiplication:
We begin with the number 3.
Multiply 3 by itself:
Multiply the result by 3 again:
Therefore, the cube of 3 is 27.
Mathematical Notation
In mathematical notation, cubing a number is represented with an exponent of 3:
This simple yet powerful operation of cubing lays the foundation for more complex mathematical concepts and calculations.
Finding the Square Root of 27
Finding the square root of a number involves determining a value which, when multiplied by itself, yields the original number. For the number 27, we want to find a number \(x\) such that \(x \times x = 27\). Let's explore the steps to find the square root of 27.
Step-by-Step Calculation
- Understanding the Square Root:
- Estimating the Square Root:
- Refining the Estimate:
- Calculating the Square Root:
The square root of 27 can be represented as \(\sqrt{27}\).
We know that \(5^2 = 25\) and \(6^2 = 36\). Therefore, \(\sqrt{27}\) lies between 5 and 6.
Using a more precise method such as the Newton-Raphson iteration or a calculator, we can find a more accurate value.
Using a calculator or iterative method, we find that:
Mathematical Representation
The calculation and representation can be summarized as:
By following these steps, we accurately determine that the square root of 27 is approximately 5.196. This precise value is useful in various mathematical and practical applications.

Mathematical Expression and Simplification
Understanding how to express and simplify the square root of 3 cubed requires a clear comprehension of exponents and roots. Let's break down the mathematical process step by step.
Initial Expression
We start with the expression for the square root of 3 cubed:
Step-by-Step Simplification
- Cubing the Number:
- Finding the Square Root:
First, calculate \(3^3\):
Next, find the square root of 27:
Alternate Simplification Method
Alternatively, we can use properties of exponents and roots to simplify the expression:
- Combine the Exponent and Root:
- Evaluate the Exponent:
Recall that the square root of a number can be written as raising that number to the power of 1/2. Thus:
Calculating \(3^{3/2}\) gives the same result:
Through these methods, we see that the square root of 3 cubed simplifies to approximately 5.196, demonstrating the power and elegance of mathematical expressions and simplifications.
Approximation and Decimal Representation
The cube of 3 is calculated as follows:
\[ 3^3 = 3 \times 3 \times 3 = 27 \]
Next, we need to find the square root of 27. The square root of 27 can be expressed as:
\[ \sqrt{27} \]
We can simplify this expression by recognizing that 27 is \(3^3\). Thus:
\[ \sqrt{27} = \sqrt{3^3} = \sqrt{3 \times 3 \times 3} = 3\sqrt{3} \]
To find the decimal representation, we need to approximate \(\sqrt{3}\). The value of \(\sqrt{3}\) is approximately 1.732. Using this approximation, we get:
\[ 3\sqrt{3} \approx 3 \times 1.732 = 5.196 \]
Therefore, the square root of 27 is approximately 5.196 in decimal form. Below is a table that summarizes the key steps and approximations:
| Step | Mathematical Expression | Approximation |
|---|---|---|
| Cube of 3 | \(3^3 = 27\) | - |
| Square Root | \(\sqrt{27} = 3\sqrt{3}\) | - |
| Approximation of \(\sqrt{3}\) | \(\sqrt{3} \approx 1.732\) | 1.732 |
| Final Approximation | \(3 \times 1.732\) | 5.196 |
Thus, the decimal representation of the square root of 27 is approximately 5.196, providing a useful and practical way to understand this mathematical concept.
Applications in Mathematics and Science
The square root of 3 cubed, which is approximately 5.196, has various applications in mathematics and science. Understanding and utilizing this value can lead to deeper insights and practical solutions in numerous fields. Here are some key applications:
- Geometry: In geometry, the square root of 3 cubed is used to calculate the length of the diagonal of a cube with side lengths of 3 units. This is derived from the Pythagorean theorem in three dimensions. For a cube with sides of length 3, the space diagonal is \( \sqrt{3^2 + 3^2 + 3^2} = \sqrt{27} \).
- Trigonometry: In trigonometry, the value is often encountered in problems involving right triangles, especially those related to 30-60-90 triangles, where the side lengths are in the ratio 1:√3:2. Here, √27 can be used to scale these ratios appropriately.
- Physics: In physics, the square root of 3 cubed appears in formulas dealing with wave mechanics and oscillations. For example, it can be used to describe the energy levels of quantum systems or the resonant frequencies of mechanical systems.
- Engineering: Engineers might use this value in designing structures that require precise measurements, such as in civil engineering for calculating forces in three-dimensional trusses or in electrical engineering for determining the impedance in AC circuits.
- Computer Science: In computer graphics, the square root of 3 cubed can help in algorithms that involve three-dimensional transformations and calculations, ensuring accurate rendering of 3D models.
- Data Analysis: When analyzing data that follow a cubic relationship, taking the square root of the cubic value can normalize data sets and simplify the interpretation of complex relationships.
These applications highlight the importance of understanding the square root of 3 cubed in various scientific and mathematical contexts. Its practical uses extend from theoretical studies to everyday problem-solving scenarios, making it a valuable concept to master.
Practical Examples and Problem Solving
The calculation of the square root of 3 cubed, \(\sqrt{27}\), can be applied in various practical scenarios in mathematics and science. Here are some detailed examples and problem-solving approaches:
Example 1: Simplifying Expressions
Consider the expression \(\sqrt{3^3}\). To simplify this:
- First, calculate \(3^3\): \[3 \times 3 \times 3 = 27\]
- Next, find the square root of 27: \[\sqrt{27} = \sqrt{3^3} = 3\sqrt{3}\]
Example 2: Solving an Equation
Suppose you need to solve the equation \(\sqrt{x^3} = 3\sqrt{3}\). To find \(x\), follow these steps:
- Square both sides of the equation to remove the square root: \[(\sqrt{x^3})^2 = (3\sqrt{3})^2\]
- This simplifies to: \[x^3 = 27\]
- Taking the cube root of both sides gives: \[x = \sqrt[3]{27} = 3\]
Example 3: Geometry Applications
In geometry, understanding roots and powers is essential. For instance, consider a cube with a volume of 27 cubic units. To find the length of each side:
- Use the formula for the volume of a cube: \[V = s^3\]
- Given \(V = 27\), solve for \(s\): \[s = \sqrt[3]{27} = 3\]
Thus, each side of the cube is 3 units long.
Example 4: Physics Problem
In physics, the concept of roots can be applied to problems involving energy and force. For example, if the energy \(E\) is proportional to the cube of distance \(d\) and \(E = 27\) when \(d = 3\), then:
- The relationship can be written as: \[E \propto d^3\]
- Given \(E = 27\) and \(d = 3\), this confirms: \[27 = 3^3\]
This example demonstrates the practical application of roots in understanding physical relationships.
Example 5: Engineering Problem
In engineering, root calculations are crucial for material strength and load calculations. For a component that can withstand a load \(L\) proportional to the square root of its volume \(V\), if \(V = 27\), then:
- Express the relationship: \[L \propto \sqrt{V}\]
- If \(V = 27\), then: \[L \propto \sqrt{27} = 3\sqrt{3}\]
This helps engineers determine the maximum load a component can handle.
These examples highlight how the concept of the square root of 3 cubed is used in various fields, demonstrating its practical importance in problem-solving.

Advanced Concepts Related to Roots and Powers
In advanced mathematics, the concepts of roots and powers extend far beyond basic calculations. Understanding these advanced concepts can provide deeper insights into mathematical theories and their applications.
One important aspect to explore is the use of rational exponents. Rational exponents allow us to express roots as powers. For instance, the square root of a number can be expressed as the number raised to the power of 1/2:
\[
\sqrt{a} = a^{\frac{1}{2}}
\]
Similarly, the cube root of a number can be expressed as the number raised to the power of 1/3:
\[
\sqrt[3]{a} = a^{\frac{1}{3}}
\]
These representations are useful when simplifying expressions involving roots and powers. For example:
\[
(\sqrt[3]{a})^2 = (a^{\frac{1}{3}})^2 = a^{\frac{2}{3}}
\]
Another advanced concept is the manipulation of expressions with multiple exponents. Consider the expression:
\[
x^{\frac{2}{3}} \times x^{\frac{1}{4}} = x^{\frac{2}{3} + \frac{1}{4}} = x^{\frac{11}{12}}
\]
Here, we use the property of exponents that allows us to add the exponents when multiplying terms with the same base.
Roots and powers also play a crucial role in solving equations. For example, consider solving the equation:
\[
\sqrt[5]{\sqrt{x}} = x^{\frac{1}{10}}
\]
We can use rational exponents to simplify and solve such equations, which is particularly useful in calculus and higher-level algebra.
In addition to rational exponents, irrational exponents also have significant applications. An irrational exponent, such as \(2^{\sqrt{2}}\), can be approximated using successive rational approximations:
\[
2^{1.4}, 2^{1.41}, 2^{1.414}, \ldots
\]
These approximations converge to the desired value of \(2^{\sqrt{2}}\), demonstrating how irrational exponents can be handled in practical computations.
Finally, advanced concepts in roots and powers are essential in various fields, including physics, engineering, and computer science. They help in modeling real-world phenomena, optimizing algorithms, and solving complex problems.
Understanding these advanced concepts provides a solid foundation for further studies in mathematics and its applications.
Common Mistakes and How to Avoid Them
When working with the square root of 3 cubed (√27), there are several common mistakes students often make. Below are these mistakes and tips on how to avoid them:
-
Incorrect Simplification:
One common mistake is incorrectly simplifying the expression. For example, some might incorrectly simplify √27 as √(3^3) and then directly to 3√3, missing the correct simplification step.
Correct Approach: Remember that √27 = √(3^3) = √(9 * 3) = 3√3. Thus, √27 simplifies to 3√3. Always break down the radicand into its prime factors to simplify correctly.
-
Forgetting the Negative Root:
When solving equations involving square roots, students often forget that there are both positive and negative roots. For instance, solving x^2 = 27 should yield x = ±√27.
Correct Approach: Always consider both the positive and negative roots when dealing with square roots. In this case, x = ±3√3.
-
Misinterpreting the Square Root Symbol:
Another mistake is misinterpreting the square root symbol as only producing the principal (positive) root, leading to incomplete solutions in some contexts.
Correct Approach: Understand that while √27 typically refers to the principal root (3√3), in equations like x^2 = 27, both roots must be considered.
-
Errors in Applying Properties of Roots:
Students might incorrectly apply properties of roots, such as assuming √(a * b) = √a * √b in all cases without recognizing domain restrictions.
Correct Approach: Always ensure that the values under the square root are non-negative before applying such properties. In cases involving complex numbers, different rules may apply.
-
Incorrectly Assuming Linearity:
Many errors arise from the incorrect assumption that operations involving roots are linear, such as believing (a + b)^2 = a^2 + b^2.
Correct Approach: Always use the correct algebraic identities, such as (a + b)^2 = a^2 + 2ab + b^2, to avoid such mistakes.
By being aware of these common mistakes and following the correct approaches, students can improve their accuracy and understanding when working with square roots and other mathematical operations.
Conclusion and Summary
In this guide, we explored the mathematical operation of finding the square root of 3 cubed, which can be expressed as \( \sqrt{3^3} \). This process led us to the number \( \sqrt{27} \), which simplifies to \( 3\sqrt{3} \). Understanding this concept requires a solid grasp of both square roots and cube roots, as well as their properties and applications.
Key points covered in this guide include:
- The definition and calculation of square and cube roots.
- The mathematical foundation and simplification process for \( \sqrt{27} \).
- Approximation techniques for non-perfect squares and cubes.
- Real-world applications in mathematics and science, showcasing the importance of these operations in various fields.
- Common mistakes to avoid when dealing with roots and powers, ensuring accurate calculations.
By understanding these concepts, you can better appreciate the relationship between squares, cubes, and their respective roots. Whether you're solving mathematical problems or applying these principles in scientific contexts, this knowledge forms a crucial part of your mathematical toolkit.
In conclusion, mastering the operations of roots and powers not only enhances your problem-solving skills but also provides a deeper insight into the mathematical structures that underpin many scientific theories and real-world applications. Keep practicing and exploring these concepts to further solidify your understanding and proficiency.
READ MORE:
Khám phá cách tính căn bậc hai và căn bậc ba trong toán học qua video hướng dẫn của Thầy J. Hướng dẫn chi tiết và dễ hiểu giúp bạn nắm vững các khái niệm cơ bản.
Căn Bậc Hai và Căn Bậc Ba | Toán Học với Thầy J