Cube Root of 3/4: Exploring Its Calculation and Applications

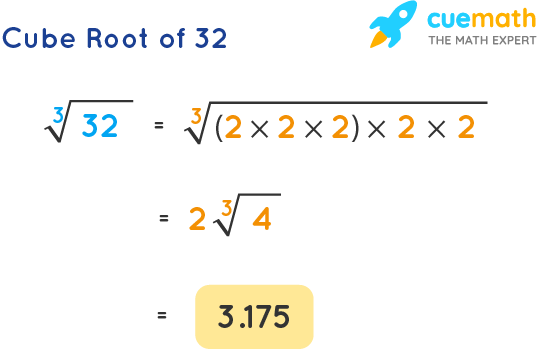
The cube root of a fraction can be found by taking the cube root of the numerator and the cube root of the denominator separately. In this case, we are looking at the cube root of $\frac{3}{4}$. Here’s a detailed breakdown:

Calculating the Cube Root

The cube root of $\frac{3}{4}$ can be expressed as:

This means we need to find:

• The cube root of 3: $3^{\frac{1}{3}}$
• The cube root of 4: $4^{\frac{1}{3}}$

Let's denote the cube root of $3$ as $\sqrt[3]{3}$ and the cube root of $4$ as $\sqrt[3]{4}$.

Approximate Values

The approximate values for these cube roots are:

• $\sqrt[3]{3}$ ≈ 1.442
• $\sqrt[3]{4}$ ≈ 1.587

Therefore, the cube root of $\frac{3}{4}$ is approximately:

Exact Value

The exact value in radical form is:

Conclusion

To summarize, the cube root of $\frac{3}{4}$ is:

• Approximately 0.909 when expressed as a decimal.
• $\frac{\sqrt[3]{3}}{\sqrt[3]{4}}$ in radical form.

This helps in understanding and calculating cube roots for fractions.

Cube roots are essential in understanding the deeper aspects of mathematics. They are used to find a number which, when multiplied by itself three times, results in the original number. For example, the cube root of 27 is 3, because $3^3$ = 27.

In mathematical notation, the cube root of a number x is represented as $\sqrt[3]{\mathrm{x}}$, or equivalently x^1/3. Here's how you can understand and calculate cube roots:

• Whole Numbers: For a number like 8, the cube root is 2 because $2^3$ = 8.
• Fractions: The cube root of a fraction involves taking the cube root of both the numerator and the denominator separately. For instance, the cube root of $\frac{3}{4}$ involves finding the cube roots of 3 and 4.
• Decimals: Calculating the cube root of a decimal is similar to whole numbers but requires more precision. For example, the cube root of 0.125 is 0.5 because ${0.5}^3$ = 0.125.

Understanding cube roots is crucial for various applications in geometry, algebra, and real-world problem-solving. Whether it's determining volumes in three-dimensional space or solving complex equations, cube roots play a pivotal role.

Let's delve deeper into the cube root of $\frac{3}{4}$ to uncover its properties and significance in mathematical contexts.

Calculating the cube root of a fraction involves breaking down the fraction into its individual components—the numerator and the denominator—and finding their cube roots separately. This method allows for a clearer understanding and more straightforward computation. Let’s explore this process step by step with the example of the fraction $\frac{3}{4}.$

1. Identify the Fraction: We start with the fraction $\frac{3}{4}.\; Our\; goal\; is\; to\; find\; the\; cube\; root\; of\; this\; fraction,\; which\; we\; denote\; as$ \sqrt[3]{\frac{3}{4}}$.$
2. Separate the Numerator and Denominator: We take the cube root of the numerator and the denominator individually:
   • $\sqrt[3]{3}$ - Cube root of 3
   • $\sqrt[3]{4}$ - Cube root of 4
3. Calculate the Cube Roots: We approximate these cube roots:
   • $\sqrt[3]{3}$ ≈ 1.442
   • $\sqrt[3]{4}$ ≈ 1.587

   Thus, $\sqrt[3]{\frac{3}{4}}$ ≈ $\frac{1.442}{1.587}$ ≈ 0.909.

4. Express the Result: The cube root of the fraction $\frac{3}{4}$ can be written as:
   • $\frac{\sqrt[3]{3}}{\sqrt[3]{4}}$ in its exact form.
   • Approximately 0.909 when expressed as a decimal.

This step-by-step process demonstrates how the cube root of a fraction can be calculated by handling the numerator and denominator separately. This approach simplifies the computation and aids in understanding the properties of fractional cube roots.

The cube root of a fraction, such as $\frac{3}{4},\; involves\; determining\; a\; number\; which,\; when\; multiplied\; by\; itself\; three\; times,\; equals\; the\; original\; fraction.\; This\; process\; can\; be\; broken\; down\; mathematically\; as\; follows:$

1. Understanding the Cube Root Notation:

   The cube root of a number x is represented as $\sqrt[3]{\mathrm{x}}$ or equivalently x^1/3. When applied to a fraction, this notation is extended to both the numerator and the denominator. For the fraction $\frac{3}{4},\; we\; write\; the\; cube\; root\; as:$

   $$
   
   
   3
   4
   
   3
   
   

2. Separating Numerator and Denominator:

   To simplify, we calculate the cube roots of the numerator and the denominator individually:

   • The cube root of 3: $\sqrt[3]{3}$
   • The cube root of 4: $\sqrt[3]{4}$

   Thus, we express the cube root of $\frac{3}{4}as:$

   $$
   
   
   3
   3
   
   
   4
   3
   
   
   

3. Exact Radical Form:

   In exact form, this fraction remains as a combination of the cube roots of the numerator and the denominator:

   $$
   
   
   3
   3
   
   
   4
   3
   
   
   

   This expression is the precise representation of the cube root of $\frac{3}{4}.$

4. Approximate Decimal Value:

   For practical purposes, we often use the approximate decimal values:

   • The cube root of 3 is approximately 1.442.
   • The cube root of 4 is approximately 1.587.

   So, the cube root of $\frac{3}{4}is\; approximately:$

   $$
   
   1.442
   1.587
   ≈ 0.909
   

By understanding and applying these steps, we can accurately compute and interpret the cube root of any fraction, such as $\frac{3}{4}.$

Finding the cube root of a fraction like $\frac{3}{4}involves\; both\; exact\; and\; approximate\; approaches.\; Understanding\; these\; values\; helps\; in\; various\; mathematical\; and\; practical\; contexts.\; Let\text{'}s\; explore\; these\; methods\; in\; detail:$

Exact Value

The exact value of the cube root of $\frac{3}{4}can\; be\; represented\; in\; radical\; form.\; By\; separately\; taking\; the\; cube\; roots\; of\; the\; numerator\; and\; the\; denominator,\; we\; get:$

$$


3
3


4
3

This expression represents the exact value without any approximation. It retains the precision of the cube roots of 3 and 4.

Approximate Values

In many cases, we use approximate decimal values to make calculations more manageable. Here's how we find the approximate value for the cube root of $\frac{3}{4}:$

1. Cube Root of the Numerator:

   The cube root of 3 can be approximated as:

   $\sqrt[3]{3}$ ≈ 1.442

2. Cube Root of the Denominator:

   The cube root of 4 can be approximated as:

   $\sqrt[3]{4}$ ≈ 1.587

3. Approximate Fraction:

   Using these approximations, the cube root of $\frac{3}{4}is:$

   $$
   
   1.442
   1.587
   ≈ 0.909
   

This approximate value is useful in various practical applications where exact precision is not required.

Comparison and Usage

Both the exact and approximate values have their place in mathematical calculations:

• Exact Values: These are essential in pure mathematics and theoretical studies where precision is critical.
• Approximate Values: These are often used in applied mathematics, engineering, and everyday problem-solving where an exact value is impractical.

Understanding both methods allows for flexibility and accuracy in various mathematical contexts.

Calculating the cube root of a fraction like $\frac{3}{4}involves\; a\; systematic\; approach\; that\; simplifies\; the\; process.\; Here,\; we\; will\; outline\; the\; step-by-step\; method\; to\; find\; both\; the\; exact\; and\; approximate\; cube\; roots\; of\; this\; fraction.$

Step-by-Step Calculation

1. Understanding the Cube Root Operation:

   The cube root of a fraction $\frac{3}{4}is\; found\; by\; separately\; calculating\; the\; cube\; roots\; of\; the\; numerator\; and\; the\; denominator.\; Mathematically,\; this\; is\; represented\; as:$

   $\sqrt[3]{\frac{3}{4}}=\frac{\sqrt[3]{3}}{\sqrt[3]{4}}$

2. Calculating the Cube Root of the Numerator:

   First, we find the cube root of 3:

   $\sqrt[3]{3}=\; 31/3$

   This value can be expressed exactly as $\sqrt[3]{3}$ or approximately as 1.442.

3. Calculating the Cube Root of the Denominator:

   Next, we find the cube root of 4:

   $\sqrt[3]{4}=\; 41/3$

   This value can be expressed exactly as $\sqrt[3]{4}$ or approximately as 1.587.

4. Forming the Fraction:

   We combine the cube roots of the numerator and the denominator to get:

   $\frac{\sqrt[3]{3}}{\sqrt[3]{4}}=\frac{1.442}{1.587}\approx \; 0.909$

   This gives us the approximate value of the cube root of $\frac{3}{4}.$

Using a Calculator or Software

For more precise or complex calculations, using a scientific calculator or software can simplify the process:

• Scientific Calculators: Enter the fraction $\frac{3}{4}and\; use\; the\; cube\; root\; function\; (often\; denoted\; as$∛).
• Software Tools: Programs like MATLAB, Python, or online calculators can quickly compute cube roots to several decimal places.

Practical Applications

Understanding how to calculate cube roots is beneficial in various fields, including physics, engineering, and finance, where such operations help solve problems involving volumes and ratios.

By following these steps, you can effectively calculate the cube root of any fraction, including $\frac{3}{4},\; and\; apply\; these\; techniques\; in\; diverse\; mathematical\; scenarios.$

The cube root of a fraction, such as $\frac{3}{4},\; is\; not\; just\; a\; theoretical\; concept\; but\; has\; practical\; applications\; across\; various\; fields.\; Understanding\; how\; to\; apply\; this\; mathematical\; operation\; can\; provide\; insights\; and\; solutions\; in\; everyday\; problems\; and\; professional\; disciplines.\; Here’s\; how\; the\; cube\; root\; of$ \frac{3}{4}can\; be\; used\; in\; real-world\; scenarios:$$

1. Engineering and Design

Engineers frequently deal with calculations involving volumes and scaling factors. The cube root is essential in determining dimensions when scaling models up or down.

• Volume Scaling: When resizing objects, knowing the cube root helps in adjusting dimensions proportionally. For instance, if an object is scaled down by a factor of $\frac{3}{4},\; the\; volume\; changes\; by\; the\; cube\; of\; this\; factor.\; To\; find\; the\; new\; dimensions,\; we\; use\; the\; cube\; root:$

$\frac{\sqrt[3]{3}}{\sqrt[3]{4}}\approx \; 0.909$ times the original dimension.

• Density and Material Properties: In materials science, the cube root is used to relate the density and volume of substances. For a material compressed to 3/4 of its original volume, the new density can be derived using the cube root.

2. Physics and Natural Sciences

In physics, the cube root is often used in formulas involving cubic relationships, such as those related to energy, force, and other physical properties.

• Wave and Sound Analysis: The cube root function appears in the analysis of waves and sound propagation, especially when examining the intensity and amplitude relationships. For example, if the intensity of sound decreases to 3/4 of its original value, the amplitude changes by the cube root of 3/4.
• Thermodynamics: In thermodynamics, the cube root is used to calculate changes in volume under different pressure and temperature conditions. If the volume of a gas is reduced to 3/4, its new temperature or pressure can be found using the cube root.

3. Finance and Economics

Financial models and economic theories often involve growth rates and scaling factors that use the cube root to determine long-term projections and trends.

• Compound Interest and Growth Rates: When calculating the growth of investments or populations, the cube root helps to find the average annual growth rate over a specified period. For instance, if an investment grows to 3/4 of its original size over three years, the average annual growth rate is given by the cube root of 3/4.
• Risk Assessment: In risk management, the cube root is used to analyze changes in market conditions and asset values, particularly when assessing the impact of scaling down operations or investments by a factor of 3/4.

4. Everyday Problem Solving

Understanding the cube root can also simplify various day-to-day calculations and estimations.

• Cooking and Recipes: When adjusting recipes, the cube root helps in scaling ingredients. For example, if you want to prepare 3/4 of a recipe, you can adjust the quantities by taking the cube root of 3/4 to ensure even cooking and consistency.
• DIY Projects: In home improvement and DIY projects, the cube root helps in resizing and reshaping materials. If you’re reducing the size of a storage box to 3/4 of its original volume, you can use the cube root to find the new dimensions accurately.

By understanding how to calculate and apply the cube root of $\frac{3}{4},\; you\; can\; solve\; a\; wide\; range\; of\; practical\; problems\; efficiently,\; from\; complex\; engineering\; tasks\; to\; everyday\; activities.$

The cube root of a number is the value that, when multiplied by itself three times, gives the original number. To visualize the cube root of 3/4 on a number line, follow these steps:

1. **Understand the Approximate Value**: The cube root of 3/4 (∛(3/4)) can be approximated using a calculator, giving approximately 0.908. This value lies between 0 and 1 on the number line.

2. **Locate Perfect Cubes for Reference**: To better understand the placement, consider the cube roots of nearby perfect cubes. For example, ∛1 = 1 and ∛(1/8) ≈ 0.5. The cube root of 3/4 will be between these two values.

3. **Plotting the Value**: Mark the points for 0, 0.5, and 1 on the number line. Since 0.908 is closer to 1, place a point slightly to the left of 1 to represent ∛(3/4).

4. **Graphical Representation**: For a more accurate visual, consider using a graphing tool or software. You can plot the function y = ∛x and see where x = 3/4 intersects the curve. This intersection gives the cube root value on the y-axis.

1. Draw a number line and mark it with evenly spaced points representing integers and fractions.
2. Identify the approximate location for 0.908 between 0 and 1.
3. Mark this point and label it as ∛(3/4).

5. **Mathematical Verification**: To ensure accuracy, verify by cubing the approximate value:
$$

0.908
3

=
0.749

, which is close to 3/4, confirming our plot.

By following these steps, you can visualize the cube root of 3/4 on a number line, providing a clearer understanding of its position relative to other numbers.

The concept of cube roots extends across various mathematical disciplines and applications. Here, we will explore how cube roots are used in different contexts, from basic arithmetic to complex numbers.

1. Basic Arithmetic and Algebra

In basic arithmetic, the cube root of a number \(a\) is a value \(b\) such that \(b^3 = a\). For example, \(\sqrt[3]{27} = 3\) because \(3^3 = 27\). The cube root is denoted by the radical symbol \(\sqrt[3]{}\).

For fractions, the cube root can be calculated by taking the cube root of the numerator and the denominator separately:

\[
\sqrt[3]{\frac{27}{8}} = \frac{\sqrt[3]{27}}{\sqrt[3]{8}} = \frac{3}{2}
\]

2. Geometry and Volume

In geometry, cube roots are used to determine the side length of a cube when its volume is known. For instance, if the volume of a cube is 64 cubic units, the side length \(s\) is:

\[
s = \sqrt[3]{64} = 4
\]

This is because \(4^3 = 64\).

3. Complex Numbers

Cube roots also play a significant role in the realm of complex numbers. When dealing with complex numbers, finding the cube root can be more intricate as it involves polar coordinates and De Moivre's theorem. For a complex number \(z\), there are generally three distinct cube roots.

For example, the cube roots of \(1\) are \(1\), \(\frac{-1 + \sqrt{3}i}{2}\), and \(\frac{-1 - \sqrt{3}i}{2}\).

4. Real-World Applications

Cube roots are used in various real-world applications, such as in engineering to determine the dimensions of objects given their volume, and in physics for calculations involving the properties of materials under different conditions.

5. Simplifying Radical Expressions

In algebra, simplifying expressions involving cube roots can be necessary. The process involves breaking down the radicand into its prime factors and then simplifying:

\[
\sqrt[3]{54} = \sqrt[3]{27 \times 2} = \sqrt[3]{27} \times \sqrt[3]{2} = 3\sqrt[3]{2}
\]

6. Solving Equations

Cube roots are used to solve cubic equations. For example, to solve \(x^3 = 8\), one would take the cube root of both sides to find \(x = 2\).

Understanding cube roots in these various contexts enhances one's ability to solve problems across different areas of mathematics and its applications.

Calculating the cube root of a number can be approached using various tools and techniques. Below, we will discuss some common methods, including manual calculation techniques and using digital tools.

Manual Calculation Techniques

One of the primary manual techniques is the prime factorization method. This involves breaking down the number into its prime factors and then simplifying:

1. Find the prime factors of the number. For example, to find the cube root of 27, express it as \( 27 = 3 \times 3 \times 3 \).
2. Group the factors into triples. Since \( 27 = 3^3 \), we see that the cube root of 27 is \( 3 \).

For non-perfect cubes, the process is more complex and may involve iterative methods to approximate the value. For example, to find the cube root of 2, you might start with an estimate and refine it using methods like Newton's method.

Using Calculators

Modern calculators and digital tools can simplify the process significantly:

• Basic Calculators: Many calculators have a cube root function (∛). Simply input the number and use the function to get the result.
• Scientific Calculators: For more precision, scientific calculators allow you to enter fractional exponents. For instance, the cube root of \( \frac{3}{4} \) can be calculated by raising the fraction to the power of \( \frac{1}{3} \).

Here's a step-by-step guide to finding the cube root using a regular calculator:

1. Type the number for which you need to find the cube root.
2. Press the root key twice, followed by the multiplication sign, and repeat this process three times.
3. Finally, press the equal sign to get the result.

Using Online Tools

Several online calculators and software can quickly compute cube roots. These tools are particularly useful for complex numbers and large datasets:

• : Provides step-by-step solutions for cube roots and other mathematical problems.
• : Offers a dedicated cube root calculator for precise calculations.
• : Offers educational resources and tools for learning and calculating cube roots.

Example: Cube Root of 3/4

To illustrate, let's calculate the cube root of \( \frac{3}{4} \) using a scientific approach:

1. Express \( \frac{3}{4} \) as \( (3/4)^{1/3} \).
2. Using a calculator or software, raise \( 3/4 \) to the power of \( 1/3 \).
3. The approximate result is \( 0.9086 \).

By leveraging these techniques and tools, calculating cube roots becomes a straightforward process, whether you prefer manual methods or modern digital aids.

Here are some common questions and detailed answers about cube roots to help you better understand this mathematical concept:

• What is a cube root?

  A cube root of a number \( x \) is a number \( y \) such that \( y^3 = x \). It is denoted as \( \sqrt[3]{x} \) or \( x^{1/3} \).

• How is the cube root of a fraction calculated?

  To find the cube root of a fraction, you can take the cube root of the numerator and the denominator separately. For example, \( \sqrt[3]{\frac{3}{4}} \) can be written as \( \frac{\sqrt[3]{3}}{\sqrt[3]{4}} \).

• What are some properties of cube roots?

  Cube roots have several unique properties:
  

  
  
  • The cube root of a positive number is positive.
  
  
  • The cube root of a negative number is negative.
  
  
  • The cube root of zero is zero.
  
  
  
  


• Can cube roots be calculated for negative numbers?

  Yes, unlike square roots, cube roots of negative numbers are real. For example, \( \sqrt[3]{-8} = -2 \) because \( (-2)^3 = -8 \).

• How do you approximate cube roots?

  You can approximate cube roots using a calculator or an iterative method like the Newton-Raphson method. For instance, the cube root of 3/4 can be approximated using a calculator to get approximately 0.9086.

• Are there any tricks to calculating cube roots mentally?

  For perfect cubes, you can memorize cubes of integers. For example, knowing that \( 2^3 = 8 \) helps you recognize that \( \sqrt[3]{8} = 2 \).

• How are cube roots used in real-world applications?

  Cube roots are used in various fields such as physics, engineering, and computer graphics to solve problems involving volumes, scaling, and more. For example, calculating the side length of a cube given its volume requires finding the cube root of the volume.

The exploration of the cube root of 3/4 has provided a comprehensive understanding of its mathematical properties, methods of calculation, and applications in various contexts. We began by defining the concept of cube roots and understanding their significance in mathematics. The cube root of 3/4, denoted as \( \sqrt[3]{\frac{3}{4}} \), is a specific example that illustrates the principles of cube roots applied to fractions.

In the section on the mathematical definition, we discussed that the cube root of a number \( x \) is a number \( y \) such that \( y^3 = x \). For the fraction 3/4, this relationship holds true as \( \left( \sqrt[3]{\frac{3}{4}} \right)^3 = \frac{3}{4} \).

We explored both exact and approximate values of the cube root of 3/4, highlighting the challenges in calculating cube roots of non-perfect cubes. Tools such as prime factorization and the use of mathematical software were emphasized as effective methods for these calculations.

The practical applications of the cube root of 3/4 were discussed, demonstrating its relevance in real-world scenarios, including volume calculations and scientific measurements. Visualizing this cube root on a number line provided a clearer understanding of its magnitude relative to other numbers.

Finally, we covered various tools and techniques for calculating cube roots, including manual methods like the long division method and modern computational tools. These techniques ensure accuracy and efficiency in finding cube roots, even for complex numbers.

In conclusion, the cube root of 3/4 is a fascinating topic that bridges theoretical mathematics and practical application. By understanding its properties and calculation methods, one can appreciate the elegance and utility of cube roots in diverse mathematical contexts.