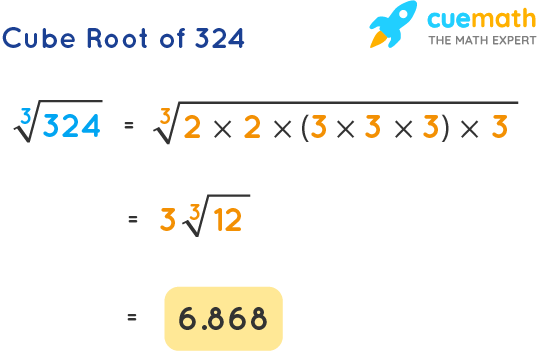
Topic what is 3 cubed: Discover the concept of "3 cubed" and learn how this fundamental mathematical operation can be easily understood and applied. This article will break down the steps of calculating 3 cubed, explain its significance in mathematics, and provide practical examples to illustrate its uses. Dive in to enhance your mathematical knowledge!
Table of Content
- Understanding 3 Cubed
- Introduction to Cubing Numbers
- Definition of 3 Cubed
- Mathematical Calculation of 3 Cubed
- Step-by-Step Calculation
- Understanding Exponentiation
- Applications of Cubed Numbers
- Visual Representation of 3 Cubed
- Examples of Cubed Numbers
- Importance of Learning Cubed Numbers
- Common Mistakes When Calculating Cubed Numbers
- Practice Problems and Solutions
- Conclusion
- YOUTUBE:
Understanding 3 Cubed
The term "3 cubed" refers to raising the number 3 to the power of 3. This can be expressed mathematically as:
\[ 3^3 \]
Calculating this involves multiplying the number 3 by itself twice more:
\[ 3 \times 3 \times 3 \]
Step-by-step, the calculation proceeds as follows:
- First, multiply 3 by 3 to get 9.
- Next, multiply 9 by 3 to get 27.
Therefore, 3 cubed equals 27:
\[ 3^3 = 27 \]
This is a basic example of an exponentiation operation, where the base (3) is raised to the power of the exponent (3).
In summary:
- Base: 3
- Exponent: 3
- Result: 27

READ MORE:
Introduction to Cubing Numbers
Cubing a number means raising it to the power of three. This mathematical operation involves multiplying the number by itself twice more. For example, when we cube the number 3, we calculate:
\[ 3^3 = 3 \times 3 \times 3 \]
This operation can be broken down into the following steps:
- First, multiply 3 by 3 to get 9:
- Next, multiply the result by 3 to get 27:
\[ 3 \times 3 = 9 \]
\[ 9 \times 3 = 27 \]
Thus, 3 cubed equals 27:
\[ 3^3 = 27 \]
Cubing numbers is a basic yet essential concept in mathematics. It forms the foundation for more complex operations and helps in understanding higher-dimensional shapes, volumes, and various algebraic equations.
Learning how to cube numbers allows for a deeper grasp of exponential functions and their applications in real-world scenarios, such as calculating volumes of cubes and other geometric shapes.
Definition of 3 Cubed
The term "3 cubed" refers to the operation of raising the number 3 to the power of 3. In mathematical notation, this is expressed as:
\[ 3^3 \]
When we say a number is cubed, we mean that it is multiplied by itself two more times. For 3 cubed, the calculation proceeds as follows:
- First, multiply 3 by itself to get 9:
- Next, multiply the result by 3 again to get 27:
\[ 3 \times 3 = 9 \]
\[ 9 \times 3 = 27 \]
Therefore, 3 cubed is equal to 27:
\[ 3^3 = 27 \]
Cubing a number is a specific case of exponentiation where the exponent is 3. This operation is foundational in mathematics, particularly in geometry, where it is used to calculate the volume of cubes and other three-dimensional shapes.
Understanding how to cube a number is crucial for solving higher-level mathematical problems and for practical applications in various fields such as engineering, physics, and computer science.
Mathematical Calculation of 3 Cubed
Calculating 3 cubed involves multiplying the number 3 by itself two more times. This process can be detailed in the following steps:
- Start with the base number 3.
- Multiply 3 by itself to find the square of 3:
- Multiply the result by 3 again to find the cube of 3:
\[ 3 \times 3 = 9 \]
\[ 9 \times 3 = 27 \]
Thus, the mathematical calculation for 3 cubed is:
\[ 3^3 = 3 \times 3 \times 3 = 27 \]
This calculation shows that when the number 3 is raised to the power of 3, the result is 27. This operation is a specific example of exponentiation, where the base number is 3 and the exponent is 3.
Cubing numbers is a fundamental concept in mathematics, often used in various fields such as geometry, where it helps calculate the volume of cubes and other three-dimensional shapes. Understanding how to perform this calculation is essential for progressing in more advanced mathematical studies and practical applications.
Step-by-Step Calculation
Calculating 3 cubed involves multiplying the number 3 by itself two more times. Here is a detailed step-by-step guide:
- Start with the base number 3.
- Multiply 3 by itself to get the first product:
- Take the result from the first multiplication (which is 9) and multiply it by 3 again:
- Thus, the final result of 3 cubed is 27:
\[ 3 \times 3 = 9 \]
\[ 9 \times 3 = 27 \]
\[ 3^3 = 27 \]
This process can also be visualized using a multiplication table:
| Step | Operation | Result |
| 1 | \( 3 \times 3 \) | 9 |
| 2 | \( 9 \times 3 \) | 27 |
Therefore, the step-by-step calculation confirms that cubing the number 3 yields 27. This method ensures that the operation is performed correctly and helps reinforce the understanding of exponentiation.
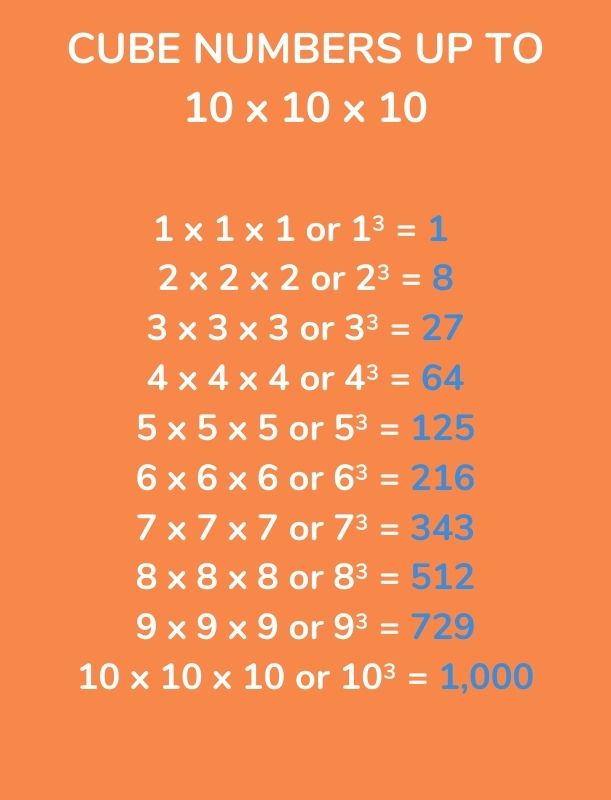
Understanding Exponentiation
Exponentiation is a mathematical operation that involves raising a number, called the base, to the power of an exponent. It is a shorthand way of expressing repeated multiplication of the same factor. For example, in the expression \(3^3\), 3 is the base and 3 is the exponent.
The general form of exponentiation is:
baseexponent = base × base × ... × base (repeated exponent times)
Here are some key points to understand about exponentiation:
- Base: The number that is being multiplied.
- Exponent: The number of times the base is multiplied by itself.
- Result: The outcome of the exponentiation operation.
In the case of \(3^3\):
- The base is 3.
- The exponent is 3.
- The calculation is 3 × 3 × 3.
Thus, \(3^3\) = 27.
Exponentiation can be visualized geometrically when dealing with perfect cubes. For example, a cube with each side of length 3 units can be thought of as being made up of smaller unit cubes. The total number of these unit cubes is \(3^3\), or 27.
Properties of Exponentiation
- Multiplication Rule: \(a^m × a^n = a^{m+n}\)
- Division Rule: \(\frac{a^m}{a^n} = a^{m-n}\)
- Power of a Power: \((a^m)^n = a^{m×n}\)
- Power of a Product: \((ab)^n = a^n × b^n\)
- Zero Exponent Rule: \(a^0 = 1\) (where a ≠ 0)
- Negative Exponent Rule: \(a^{-n} = \frac{1}{a^n}\)
Applications of Exponentiation
Exponentiation is used in various fields such as science, engineering, and finance. It is crucial for understanding growth rates, calculating compound interest, and in algorithms for computing large powers efficiently.
For instance, in finance, compound interest calculations rely heavily on exponentiation to determine the growth of investments over time. In computing, algorithms for encryption and decryption often use exponentiation due to its properties and efficiency.
Applications of Cubed Numbers
Cubed numbers, such as 3 cubed (3^3), which equals 27, have a variety of applications across different fields. Understanding these applications helps to appreciate the practical relevance of this mathematical concept.
-
Volume Calculations:
In geometry, cubed numbers are essential for calculating the volume of three-dimensional objects. For example, the volume of a cube with side length 3 is calculated as \(3 \times 3 \times 3 = 27\) cubic units. This principle applies to other cubic and rectangular shapes in construction and design.
-
Engineering:
Engineers use cubed numbers when dealing with spatial dimensions of structures and materials. For instance, when designing buildings or machinery, calculating the volume is crucial for determining the capacity and material requirements.
-
Physics:
Cubed numbers appear in physics, particularly in formulas involving volume, density, and other three-dimensional measurements. For example, the displacement of objects in fluid dynamics often requires calculations involving cubed values.
-
Mathematical Puzzles and Games:
Many puzzles and educational games incorporate cubed numbers to enhance spatial reasoning and problem-solving skills. For example, puzzles that involve arranging blocks or figuring out volumes often rely on understanding cubes.
-
Computer Graphics:
In computer graphics, cubed numbers are used to model three-dimensional objects and environments. Calculating the volume and scaling of 3D models involves using cubed values.
-
Cooking and Baking:
Recipes sometimes require precise volume measurements, which involve understanding cubic measurements. For instance, knowing the volume of a cubic container can help in determining the amount of ingredients needed.
-
Scientific Research:
In scientific research, cubed numbers are used in various calculations, such as determining the concentration of substances in a given volume or analyzing spatial data in environmental studies.
By exploring these applications, we see that cubed numbers are not just abstract mathematical concepts but have practical uses that impact everyday life and advanced scientific endeavors.
Visual Representation of 3 Cubed
Visualizing 3 cubed (33) helps in understanding the concept of cubing a number. When we say 3 cubed, we mean multiplying 3 by itself twice more, resulting in 27. This can be represented geometrically using a cube.
Here's a step-by-step explanation:
- Geometric Cube: Imagine a cube with each side of length 3 units. A cube has six faces, each face being a square.
- Volume Calculation: The volume of the cube is calculated by multiplying the side length by itself three times:
- Unit Cubes: This volume can be visualized by fitting 27 smaller unit cubes (each 1x1x1) inside the larger cube.
Below is a simple table representation of how the smaller cubes fit into the larger cube:
| Layer | Number of Cubes |
|---|---|
| 1st Layer | 9 (3x3) |
| 2nd Layer | 9 (3x3) |
| 3rd Layer | 9 (3x3) |
| Total | 27 |
Understanding 3 cubed through visual representation not only aids in grasping the multiplication concept but also shows how numbers can translate into three-dimensional space. This is a fundamental idea in geometry and can be extended to higher powers and dimensions.
Examples of Cubed Numbers
Cubed numbers, also known as cube numbers, are the result of a number being multiplied by itself twice. Here are some examples:
- 1³ = 1 × 1 × 1 = 1
- 2³ = 2 × 2 × 2 = 8
- 3³ = 3 × 3 × 3 = 27
- 4³ = 4 × 4 × 4 = 64
- 5³ = 5 × 5 × 5 = 125
- 6³ = 6 × 6 × 6 = 216
- 7³ = 7 × 7 × 7 = 343
- 8³ = 8 × 8 × 8 = 512
- 9³ = 9 × 9 × 9 = 729
- 10³ = 10 × 10 × 10 = 1000
Cubing numbers can be useful in various mathematical contexts, including finding the volume of a cube. For example, a cube with a side length of 3 units has a volume of 27 cubic units, as demonstrated by the calculation 3³ = 27.
Here is a more extensive list of cubed numbers up to 100:
- 11³ = 1331
- 12³ = 1728
- 13³ = 2197
- 14³ = 2744
- 15³ = 3375
- 16³ = 4096
- 17³ = 4913
- 18³ = 5832
- 19³ = 6859
- 20³ = 8000
Continuing this pattern, here are some higher cubed numbers:
- 21³ = 9261
- 22³ = 10648
- 23³ = 12167
- 24³ = 13824
- 25³ = 15625
Understanding and working with cubed numbers can help in various areas of mathematics, including algebra, geometry, and more advanced topics like calculus. They are particularly useful in solving problems related to volume and in recognizing patterns in number theory.

Importance of Learning Cubed Numbers
Understanding cubed numbers is essential for several reasons:
- Foundation in Mathematics: Cubed numbers are a fundamental concept in mathematics, helping to build a strong foundation for more complex topics such as algebra, geometry, and calculus.
- Real-World Applications: Cubed numbers are used in various real-world applications, including physics, engineering, and computer science. For example, calculating volumes of cubes and cuboids relies on understanding cubed numbers.
- Problem-Solving Skills: Learning about cubed numbers enhances problem-solving skills and logical thinking. It helps students approach problems methodically, breaking them down into manageable steps.
- Advanced Mathematics: A solid grasp of cubed numbers is crucial for tackling advanced mathematical concepts such as polynomial functions and complex number theory.
- Scientific Understanding: Many scientific principles, such as those in chemistry and physics, involve cubed numbers. For instance, understanding the relationships between different physical quantities often requires knowledge of exponentiation.
By mastering cubed numbers, students not only excel in their current studies but also prepare themselves for future academic and professional challenges.
Common Mistakes When Calculating Cubed Numbers
Calculating cubed numbers can sometimes be challenging, and there are several common mistakes that people often make. Understanding these mistakes can help in avoiding them and improving accuracy in calculations. Here are some of the most frequent errors:
-
Misunderstanding the Concept of Cubing:
One common mistake is confusing cubing with multiplying by three. Cubing a number means raising it to the power of three, not simply multiplying it by three. For example, \(3^3 = 3 \times 3 \times 3 = 27\), not \(3 \times 3 = 9\).
-
Incorrect Order of Operations:
Another frequent error occurs when the order of operations is not followed correctly. When cubing numbers within a mathematical expression, it is crucial to apply the exponentiation before any multiplication, addition, or subtraction. For instance, in the expression \(2 + 3^3\), you must calculate \(3^3 = 27\) first, then add 2, resulting in 29, not \(5^3\).
-
Forgetting to Cube Negative Numbers Properly:
Negative numbers cubed remain negative, but sometimes this is overlooked. For example, \((-2)^3 = -2 \times -2 \times -2 = -8\), not 8.
-
Errors with Large Numbers:
When cubing large numbers, it's easy to make mistakes in the multiplication steps. Using a calculator or breaking the problem into smaller parts can help. For example, \(12^3\) can be calculated as \(12 \times 12 = 144\), then \(144 \times 12 = 1728\).
-
Mistakes with Decimal Numbers:
Decimals can be tricky. Ensure that each multiplication is done correctly. For instance, \(1.2^3\) should be calculated as \(1.2 \times 1.2 = 1.44\), and then \(1.44 \times 1.2 = 1.728\).
-
Misapplying the Distributive Property:
When working with cubed binomials, remember that \((a + b)^3 \neq a^3 + b^3\). Instead, use the binomial expansion: \((a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3\).
By being aware of these common mistakes and understanding how to avoid them, you can improve your accuracy when calculating cubed numbers.
Practice Problems and Solutions
Here are some practice problems to help you understand how to calculate cubed numbers. Try solving these on your own before checking the solutions.
-
Calculate \(2^3\).
Solution:
\(2^3 = 2 \times 2 \times 2 = 8\)
-
Calculate \(4^3\).
Solution:
\(4^3 = 4 \times 4 \times 4 = 64\)
-
Calculate \(5^3\).
Solution:
\(5^3 = 5 \times 5 \times 5 = 125\)
-
Calculate \(7^3\).
Solution:
\(7^3 = 7 \times 7 \times 7 = 343\)
-
Solve for the cube of \(-3\).
Solution:
\((-3)^3 = -3 \times -3 \times -3 = -27\)
For a more advanced practice, consider these problems:
-
Calculate \((2x)^3\).
Solution:
\((2x)^3 = 2^3 \times x^3 = 8x^3\)
-
Calculate \((3y)^3\).
Solution:
\((3y)^3 = 3^3 \times y^3 = 27y^3\)
-
Solve for the cube of \((4x - 2)\).
Solution:
\((4x - 2)^3 = (4x - 2) \times (4x - 2) \times (4x - 2) = 64x^3 - 96x^2 + 48x - 8\)
Practicing these problems will help reinforce your understanding of cubed numbers and their calculations. Remember to double-check your work to avoid common mistakes!
Conclusion
In conclusion, understanding and calculating cubed numbers, such as 3 cubed, is a fundamental aspect of mathematics that provides a solid foundation for more advanced concepts. Cubing a number involves multiplying the number by itself three times, which in the case of 3 cubed, results in \(27\) (i.e., \(3 \times 3 \times 3 = 27\)).
Learning about cubed numbers helps enhance problem-solving skills and mathematical reasoning. It is crucial in various fields, including geometry, physics, and computer science. For instance, calculating the volume of cubes and other three-dimensional objects relies on the principles of cubed numbers.
Moreover, mastering cubed numbers prepares students for more complex topics, such as polynomial equations and calculus. Regular practice with different cubing problems ensures a deeper understanding and ability to apply these concepts in real-world scenarios.
Overall, the knowledge of cubed numbers is not just an academic exercise but a practical tool that enriches one’s analytical capabilities and broadens the scope of mathematical applications.

Làm Thế Nào Để Lập Phương Một Số | Lập Phương Một Số Có Nghĩa Là Gì? | Số Mũ | Toán Học với Thầy J
READ MORE:
Số 3 Lập Phương Là Gì? (Câu Hỏi Mẹo 🤫😳)