Topic square root of 3 is irrational: The square root of 3 is irrational, a fact that has intrigued mathematicians for centuries. In this article, we delve into the proof of its irrationality, exploring historical context, mathematical implications, and real-world applications. Join us on this journey to understand why the square root of 3 cannot be expressed as a simple fraction.
Table of Content
- Proof that the Square Root of 3 is Irrational
- Introduction to Irrational Numbers
- Understanding Rational and Irrational Numbers
- Definition of the Square Root of 3
- Historical Context and Discovery
- Proof that the Square Root of 3 is Irrational
- Alternative Proof Methods
- Applications of the Square Root of 3 in Mathematics
- Implications in Geometry and Trigonometry
- Square Root of 3 in Real-World Problems
- Common Misconceptions and Clarifications
- Advanced Topics and Further Reading
- Conclusion and Summary
- YOUTUBE: Khám phá bằng chứng toán học rằng căn bậc hai của 3 là số vô tỉ. Video này cung cấp lời giải chi tiết và dễ hiểu để thu hút người xem.
Proof that the Square Root of 3 is Irrational
The square root of 3 is an irrational number, meaning it cannot be expressed as a fraction of two integers. Below is a detailed proof using a contradiction argument:
Proof by Contradiction
We start by assuming the opposite, that the square root of 3 is rational. This means it can be written as a fraction of two integers in simplest form.
- Assume
\(\sqrt{3} = \frac{p}{q}\) , where \(p\) and \(q\) are coprime integers (i.e., their greatest common divisor is 1). - Square both sides of the equation to obtain
\(3 = \frac{p^2}{q^2}\) . - Multiply both sides by \(q^2\) to get
\(3q^2 = p^2\) . - This implies that \(p^2\) is a multiple of 3, hence \(p\) must also be a multiple of 3 (since the square of a number divisible by 3 is also divisible by 3).
- Let \(p = 3k\) for some integer \(k\). Substituting back, we get
\(p^2 = (3k)^2 = 9k^2\) . - Substitute \(p^2\) in the equation
\(3q^2 = p^2\) to get\(3q^2 = 9k^2\) , which simplifies to\(q^2 = 3k^2\) . - This implies that \(q^2\) is also a multiple of 3, and therefore \(q\) must be a multiple of 3.
- If both \(p\) and \(q\) are multiples of 3, they have a common factor of 3. This contradicts our initial assumption that \(p\) and \(q\) are coprime.
Since our assumption that \(\sqrt{3}\) is rational leads to a contradiction, we conclude that \(\sqrt{3}\) is irrational.

READ MORE:
Introduction to Irrational Numbers
Irrational numbers are real numbers that cannot be expressed as a ratio of two integers. Unlike rational numbers, which can be written as fractions, irrational numbers have non-terminating, non-repeating decimal expansions.
Here is a step-by-step explanation to understand irrational numbers:
- Definition: An irrational number cannot be written in the form \(\frac{a}{b}\) where \(a\) and \(b\) are integers and \(b \neq 0\). Examples include \(\sqrt{2}\), \(\pi\), and \(e\).
- Decimal Representation: Irrational numbers have decimal representations that go on forever without repeating. For instance, \(\sqrt{3} \approx 1.732050807568877...\) continues indefinitely without a pattern.
- Historical Context: The concept of irrational numbers dates back to ancient Greece. The Pythagoreans discovered that \(\sqrt{2}\) could not be expressed as a fraction, leading to the realization of irrational numbers.
- Mathematical Proofs: There are various methods to prove that certain numbers are irrational. One common approach is proof by contradiction, which shows that assuming a number is rational leads to a logical inconsistency.
Understanding irrational numbers is crucial for deeper insights into mathematics. They play a vital role in various mathematical theories and applications, demonstrating the complexity and beauty of the number system.
Understanding Rational and Irrational Numbers
To grasp the concept of irrational numbers, we must first understand rational numbers. Rational numbers are numbers that can be expressed as the quotient of two integers, where the numerator is an integer and the denominator is a non-zero integer. Mathematically, a rational number can be written as:
\[ \frac{a}{b} \]
where \( a \) and \( b \) are integers, and \( b \neq 0 \).
Examples of rational numbers include:
- \(\frac{1}{2}\)
- \(3\) (which can be written as \(\frac{3}{1}\))
- \(-\frac{4}{5}\)
Irrational numbers, on the other hand, cannot be expressed as a simple fraction of two integers. These numbers have non-repeating, non-terminating decimal expansions. This means their decimal representation goes on forever without repeating a pattern. Examples of irrational numbers include:
- \(\pi\)
- \(e\) (the base of natural logarithms)
- \(\sqrt{2}\)
- \(\sqrt{3}\)
To further illustrate the difference, let's look at the decimal expansions:
| Number | Type | Decimal Expansion |
|---|---|---|
| \(\frac{1}{2}\) | Rational | 0.5 |
| \(\frac{1}{3}\) | Rational | 0.3333... |
| \(\sqrt{2}\) | Irrational | 1.414213562...\( \ldots \) |
| \(\sqrt{3}\) | Irrational | 1.732050807...\( \ldots \) |
The key difference lies in the decimal representation: rational numbers have either a finite decimal form or a repeating pattern, while irrational numbers do not.
Understanding these concepts is fundamental to delving into more advanced mathematical theories, including the proof of the irrationality of the square root of 3.
Definition of the Square Root of 3
The square root of 3, denoted as or √3, is a mathematical constant that cannot be expressed as a simple fraction. This characteristic makes it an irrational number.
In different forms, the square root of 3 can be represented as:
- Decimal form: 1.732050807...
- Radical form:
- Exponent form: 31/2
The square root of 3 is non-terminating and non-repeating when written in decimal form, which is a key property of irrational numbers.
To further understand its value, consider the following:
- It is approximately equal to 1.732, but its exact value continues indefinitely without repeating.
- This number appears frequently in geometry and trigonometry, such as in the calculation of the height of an equilateral triangle and in certain trigonometric functions.
In mathematical terms, the square root of 3 can be approximated using the following methods:
- Long Division Method: This method helps in finding the square root by repeatedly dividing and averaging.
- Continued Fractions: The square root of 3 can be expressed as a continued fraction: [1; 1, 2, 1, 2, 1, 2, ...].
Let's take a closer look at the calculation using the long division method:
- Start by writing 3 as 3.000000 and group the digits in pairs from right to left.
- Find the largest number whose square is less than or equal to 3, which is 1.
- Subtract the square (12 = 1) from 3 to get the remainder 2.
- Bring down a pair of zeros to make it 200.
- Double the current quotient (1) to get 2, and find a digit x such that 2x * x ≤ 200. This gives x = 7, so the next digit in the quotient is 7.
- Repeat the process to find more digits in the quotient.
Using these methods, one can approximate the square root of 3 to any desired precision, though it will always remain an irrational number.
Historical Context and Discovery
The history of irrational numbers dates back to ancient Greece. The concept of irrational numbers was first discovered by the Pythagoreans, a group of mathematicians and philosophers led by Pythagoras. They initially believed that all numbers could be expressed as the ratio of two integers. This belief was challenged by the discovery of irrational numbers, which cannot be expressed as such ratios.
Hippasus of Metapontum, a Pythagorean mathematician, is credited with the discovery of irrational numbers. He is believed to have demonstrated the irrationality of the square root of 2 using a geometrical proof. According to legend, this discovery was so shocking and contrary to the Pythagorean belief in the absoluteness of rational numbers that Hippasus was allegedly drowned for revealing this truth.
The understanding and acceptance of irrational numbers evolved over time. In the 16th century, the Flemish mathematician Simon Stevin declared that both rational and irrational numbers are valid and significant, and he demonstrated this on the number line. Later, mathematicians such as Rene Descartes and Leonhard Euler further developed the theory of irrational numbers.
The term "irrational" itself comes from the Latin word "irrationalis," meaning "not rational." This term was used because these numbers do not conform to the rules of rational numbers. Over the centuries, the concept of irrational numbers has become a fundamental part of mathematics, with applications in various fields including geometry, calculus, and number theory.
In summary, the discovery of irrational numbers, starting with the square root of 2 and later including numbers like the square root of 3, was a pivotal moment in the history of mathematics. It challenged long-held beliefs and expanded the understanding of number systems, laying the groundwork for modern mathematical theories.
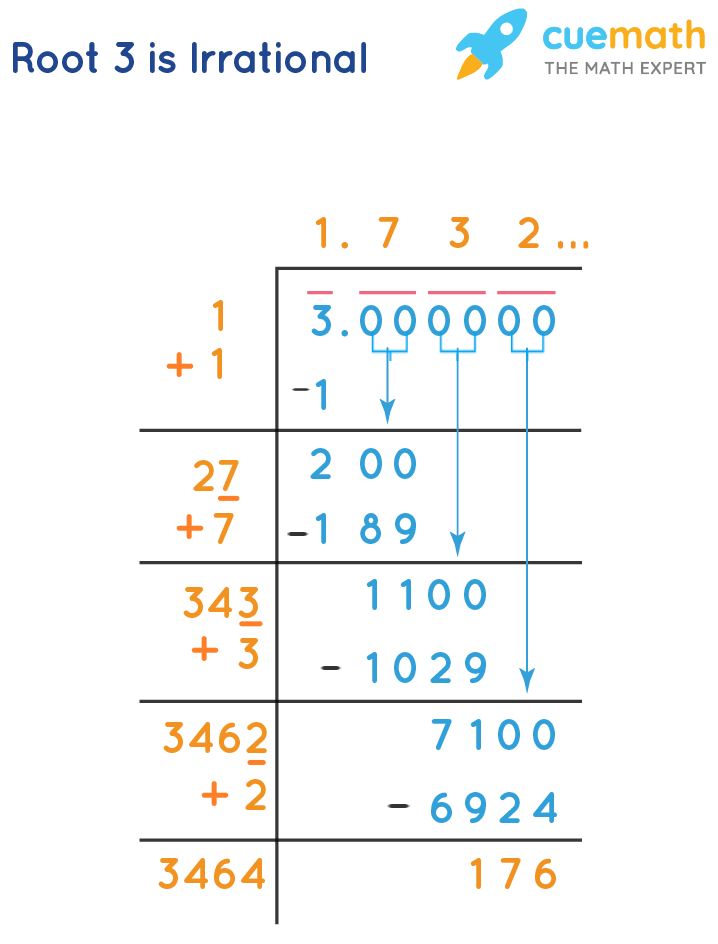
Proof that the Square Root of 3 is Irrational
To prove that the square root of 3 is irrational, we will use a proof by contradiction. We will assume that the square root of 3 is rational and then show that this assumption leads to a contradiction.
Let's assume that \(\sqrt{3}\) is rational. This means that it can be expressed as a ratio of two integers \( \frac{a}{b} \) in simplest form, where \(a\) and \(b\) have no common factors other than 1 and \(b \neq 0\). Therefore, we can write:
\[ \sqrt{3} = \frac{a}{b} \]
Squaring both sides, we get:
\[ 3 = \frac{a^2}{b^2} \]
Multiplying both sides by \( b^2 \) to clear the fraction, we have:
\[ 3b^2 = a^2 \]
This equation implies that \( a^2 \) is a multiple of 3. Therefore, \(a\) must also be a multiple of 3 (because if the square of a number is divisible by 3, the number itself must be divisible by 3). Let's write \(a\) as:
\[ a = 3k \]
where \(k\) is an integer. Substituting \(a = 3k\) back into the equation \(3b^2 = a^2\), we get:
\[ 3b^2 = (3k)^2 \]
\[ 3b^2 = 9k^2 \]
\[ b^2 = 3k^2 \]
This equation implies that \( b^2 \) is also a multiple of 3, and hence \(b\) must be a multiple of 3 as well. Therefore, \(a\) and \(b\) both have 3 as a common factor.
This contradicts our initial assumption that \( \frac{a}{b} \) is in simplest form with \(a\) and \(b\) having no common factors other than 1. Hence, our assumption that \(\sqrt{3}\) is rational must be false.
Therefore, we conclude that \(\sqrt{3}\) is irrational.
Alternative Proof Methods
In addition to the traditional proof by contradiction, there are several other methods to prove that the square root of 3 is irrational. Here, we explore some of these alternative approaches:
1. Proof by Infinite Descent
This method involves assuming the opposite of what we want to prove and showing that it leads to an infinite regress.
- Assume that \(\sqrt{3}\) is rational, so it can be written as \(\frac{a}{b}\) where \(a\) and \(b\) are co-prime integers.
- Then we have \(3b^2 = a^2\), implying that \(a^2\) is divisible by 3.
- This means \(a\) must also be divisible by 3, so let \(a = 3k\) for some integer \(k\).
- Substitute \(a\) back into the equation: \(3b^2 = (3k)^2 = 9k^2\), which simplifies to \(b^2 = 3k^2\).
- Thus, \(b^2\) is also divisible by 3, implying \(b\) is divisible by 3, contradicting the assumption that \(a\) and \(b\) are co-prime.
- This infinite regress shows that our initial assumption must be false, proving \(\sqrt{3}\) is irrational.
2. Proof by Continued Fractions
Continued fractions provide another method to prove the irrationality of \(\sqrt{3}\).
- Represent \(\sqrt{3}\) as a continued fraction, which is non-terminating and non-repeating: \[\sqrt{3} = 1 + \frac{1}{1 + \frac{1}{2 + \frac{1}{1 + \frac{1}{2 + \ldots}}}}\]
- If \(\sqrt{3}\) were rational, its continued fraction representation would terminate or repeat periodically.
- The fact that the continued fraction for \(\sqrt{3}\) does neither proves that \(\sqrt{3}\) is irrational.
3. Proof by the Rational Root Theorem
The Rational Root Theorem can also be used to show the irrationality of \(\sqrt{3}\).
- Consider the polynomial \(x^2 - 3 = 0\).
- The Rational Root Theorem states that any rational solution \(\frac{p}{q}\) must be a factor of the constant term (3) divided by a factor of the leading coefficient (1), so \(\frac{p}{q}\) must be \(\pm 1\) or \(\pm 3\).
- Neither \(\pm 1\) nor \(\pm 3\) are solutions to the equation \(x^2 - 3 = 0\), so there are no rational roots.
- Hence, \(\sqrt{3}\) cannot be rational.
These methods, along with the traditional proof by contradiction, provide a robust understanding of why \(\sqrt{3}\) is an irrational number.
Applications of the Square Root of 3 in Mathematics
The square root of 3, an irrational number denoted as \( \sqrt{3} \), plays a significant role in various branches of mathematics. Its unique properties are utilized in numerous applications, ranging from geometry to trigonometry and beyond. Below are some detailed explanations of its applications:
1. Geometry
In geometry, \( \sqrt{3} \) is crucial in the study of equilateral triangles. An equilateral triangle with sides of length 2 has a height of \( \sqrt{3} \). This relationship is derived from the Pythagorean theorem:
\[ h = \sqrt{2^2 - 1^2} = \sqrt{3} \]
This property is often used in calculating areas and heights of such triangles and in various constructions and proofs.
2. Trigonometry
The square root of 3 appears in trigonometric functions and identities. For example, the tangent of 60 degrees (or \( \pi/3 \) radians) is equal to \( \sqrt{3} \):
\[ \tan\left(\frac{\pi}{3}\right) = \sqrt{3} \]
Similarly, \( \sqrt{3} \) is also found in other trigonometric ratios and helps in solving problems involving angles of 30, 60, and 90 degrees.
3. Algebra
In algebra, \( \sqrt{3} \) is often encountered in polynomial equations and radical expressions. Solving quadratic equations that involve irrational roots can lead to expressions containing \( \sqrt{3} \), which requires understanding its properties for simplification and rationalization.
4. Calculus
In calculus, \( \sqrt{3} \) can appear in the context of limits, integrals, and series. For instance, integrals involving square roots often include \( \sqrt{3} \), requiring techniques like substitution and partial fractions for evaluation:
\[ \int \frac{dx}{\sqrt{3x+1}} \]
5. Real-World Applications
- Engineering: In fields like electrical engineering and structural engineering, \( \sqrt{3} \) is used in formulas related to three-phase power systems, where the ratio of line-to-line voltages to phase voltages is \( \sqrt{3} \).
- Physics: \( \sqrt{3} \) emerges in the study of crystal lattices and materials science, particularly in hexagonal close-packed (HCP) structures.
6. Theoretical Mathematics
In number theory and abstract algebra, the irrationality of \( \sqrt{3} \) is explored to understand the properties of numbers and their relationships. Its irrational nature makes it a key example in discussions about irrational numbers and their proofs.
The applications of \( \sqrt{3} \) extend across various mathematical disciplines, highlighting its importance and the necessity of understanding its properties in both theoretical and practical contexts.
Implications in Geometry and Trigonometry
The square root of 3 (\(\sqrt{3}\)) plays a crucial role in both geometry and trigonometry due to its presence in various mathematical constructs and its properties as an irrational number. Here, we explore some of the key implications and applications of \(\sqrt{3}\) in these fields.
Equilateral Triangles and Hexagons
An equilateral triangle, where all sides are equal, has angles of 60 degrees each. The height (altitude) of an equilateral triangle can be calculated using \(\sqrt{3}\), making it a fundamental constant in geometric calculations:
For an equilateral triangle with side length \(a\), the height \(h\) is given by:
\[
h = \frac{\sqrt{3}}{2}a
\]
This property extends to regular hexagons, which can be divided into six equilateral triangles. The relationship between the side length of the hexagon and its height also involves \(\sqrt{3}\).
30-60-90 Triangles
In trigonometry, the 30-60-90 triangle is a special right triangle where the lengths of the sides are in the ratio 1:\(\sqrt{3}\):2. The presence of \(\sqrt{3}\) here is critical for solving problems involving these triangles:
\[
\text{If the shorter leg (opposite 30 degrees) is } x, \text{ then the longer leg (opposite 60 degrees) is } x\sqrt{3}.
\]
Tangents and Slopes
In trigonometry, the tangent of a 60-degree angle is \(\sqrt{3}\). This is significant in many applications, including calculating slopes in coordinate geometry:
\[
\tan(60^\circ) = \sqrt{3}
\]
Crystals and Lattices
The geometric arrangement of atoms in certain crystal structures also involves \(\sqrt{3}\). For example, in the hexagonal close-packed structure, the ratio of certain interatomic distances involves \(\sqrt{3}\), influencing material properties.
Complex Numbers and Rotations
In the complex plane, rotations by 120 degrees (or multiples thereof) around the origin can be expressed using complex numbers involving \(\sqrt{3}\). This is particularly relevant in electrical engineering and physics where such rotations are common.
In summary, \(\sqrt{3}\) is integral to various geometric and trigonometric concepts, influencing calculations involving angles, distances, and transformations. Its irrational nature ensures precision in these applications, underscoring its importance in both theoretical and applied mathematics.

Square Root of 3 in Real-World Problems
The square root of 3, denoted as , is an irrational number that appears in various real-world applications. Here are some key examples of its practical uses:
-
Electrical Engineering:
In three-phase electrical power systems, the square root of 3 is used to calculate line-to-line voltages from line-to-neutral voltages. The relationship is given by:
-
Geometry:
The height of an equilateral triangle can be calculated using the formula involving the square root of 3. If a is the side length of the triangle, then the height h is given by:
-
Trigonometry:
In trigonometry, the value of plays a critical role in solving various problems involving angles and distances.
-
Physics:
The square root of 3 is used in the calculations involving the physics of wave interference and diffraction patterns, particularly in the study of crystal lattices and materials science.
-
Computer Science:
In computer algorithms, particularly in computational geometry, the square root of 3 is used to determine distances and optimize spatial data structures.
These examples highlight the diverse applications of the square root of 3, illustrating its importance in both theoretical and practical contexts.
Common Misconceptions and Clarifications
There are several common misconceptions about the square root of 3 and irrational numbers in general. It's important to address these misunderstandings to clarify the concept.
- Misconception 1: Irrational Numbers Can Be Written as Fractions
Many people mistakenly believe that irrational numbers, such as the square root of 3, can be expressed as simple fractions. This is not true. Irrational numbers cannot be written as a ratio of two integers.
- Clarification:
An irrational number cannot be precisely written as a/b, where a and b are integers. Their decimal expansions are non-terminating and non-repeating.
- Misconception 2: All Square Roots Are Irrational
Another common belief is that all square roots are irrational numbers. This is not the case.
- Clarification:
Only the square roots of non-perfect squares are irrational. For example, √4 is 2, which is rational, but √3 is irrational.
- Misconception 3: Rational Approximations Make Numbers Rational
Some think that because we can approximate irrational numbers with fractions, the numbers themselves become rational.
- Clarification:
Approximations do not change the nature of a number. While √3 can be approximated as 1.732, this does not make it a rational number.
- Misconception 4: Decimal Representation
There is a belief that any number with a long decimal representation is irrational.
- Clarification:
A long decimal representation does not necessarily indicate an irrational number. Rational numbers can also have long decimal expansions, but they will eventually repeat or terminate.
By understanding these common misconceptions and their clarifications, we can gain a clearer perspective on irrational numbers, particularly the square root of 3. This helps in both mathematical theory and practical applications.
Advanced Topics and Further Reading
The square root of 3 (\(\sqrt{3}\)) has numerous advanced applications and theoretical implications in various branches of mathematics. In this section, we will explore some of these advanced topics and provide references for further reading.
Advanced Proof Techniques
While the standard proof by contradiction is commonly used to show that \(\sqrt{3}\) is irrational, there are other sophisticated methods that mathematicians use to explore irrationality and transcendence of numbers.
- Continued Fractions: The representation of \(\sqrt{3}\) as an infinite continued fraction provides insights into its irrational nature and can be used to approximate \(\sqrt{3}\) with great accuracy.
- Galois Theory: This branch of abstract algebra can be employed to understand the algebraic properties of \(\sqrt{3}\) and its role in field extensions.
Applications in Number Theory
The properties of \(\sqrt{3}\) extend to various areas in number theory, influencing the study of quadratic fields and Diophantine equations.
- Quadratic Fields: \(\sqrt{3}\) is an element of the quadratic field \(\mathbb{Q}(\sqrt{3})\), which has unique factorization properties and is a key object of study in algebraic number theory.
- Diophantine Equations: Equations involving \(\sqrt{3}\) can be studied to understand the solutions to polynomial equations with integer coefficients.
Geometric Implications
The square root of 3 plays a crucial role in various geometric constructions and proofs.
- Equilateral Triangles: The height of an equilateral triangle with side length \(a\) is given by \(\frac{a\sqrt{3}}{2}\), highlighting the geometric significance of \(\sqrt{3}\).
- Hexagons: In regular hexagons, the relationship between the side length and the distance between opposite vertices involves \(\sqrt{3}\).
Further Reading
To deepen your understanding of the square root of 3 and its mathematical implications, consider exploring the following references:
- "Introduction to the Theory of Numbers" by G.H. Hardy and E.M. Wright - This classic text provides a comprehensive overview of number theory, including discussions on irrational numbers.
- "Algebraic Number Theory" by Serge Lang - A detailed exploration of number fields and algebraic integers, offering insights into the properties of numbers like \(\sqrt{3}\).
- "Continued Fractions" by A.J. van der Poorten - This book delves into the theory and applications of continued fractions, with examples involving \(\sqrt{3}\).
Conclusion and Summary
The square root of 3, often represented as \( \sqrt{3} \), holds a significant place in mathematics, especially due to its irrational nature. This means it cannot be expressed as a fraction of two integers and its decimal expansion is non-terminating and non-repeating.
Proof of Irrationality:
-
One of the most common methods to prove that \( \sqrt{3} \) is irrational is by contradiction. Assume \( \sqrt{3} \) is rational, meaning it can be written as \( \frac{a}{b} \) where \( a \) and \( b \) are integers with no common factors and \( b \neq 0 \). -
Squaring both sides gives \( 3 = \frac{a^2}{b^2} \) or \( 3b^2 = a^2 \). This implies that \( a^2 \) is divisible by 3, so \( a \) must also be divisible by 3. Let \( a = 3k \) for some integer \( k \). -
Substituting \( a \) into the equation \( 3b^2 = (3k)^2 \) gives \( 3b^2 = 9k^2 \) or \( b^2 = 3k^2 \). This means \( b^2 \) is also divisible by 3, so \( b \) must be divisible by 3. -
However, this contradicts our initial assumption that \( a \) and \( b \) have no common factors. Therefore, \( \sqrt{3} \) cannot be rational.
Applications:
-
In geometry, \( \sqrt{3} \) appears in the context of equilateral triangles and 30-60-90 triangles. For instance, the height of an equilateral triangle with a side length of 2 is \( \sqrt{3} \). -
In trigonometry, \( \sqrt{3} \) is related to certain trigonometric ratios such as \( \tan(60^\circ) = \sqrt{3} \) and \( \sin(60^\circ) = \frac{\sqrt{3}}{2} \).
Further Implications:
The irrationality of \( \sqrt{3} \) also extends to other mathematical fields, including algebra and number theory, where it is used in various proofs and theorems. For example, in continued fractions, \( \sqrt{3} \) has a unique representation which further proves its irrationality.
In conclusion, the irrationality of \( \sqrt{3} \) not only highlights the fascinating structure of numbers but also plays a crucial role in various mathematical applications and proofs. This exploration into the nature of \( \sqrt{3} \) enriches our understanding of the fundamental properties of numbers.
Khám phá bằng chứng toán học rằng căn bậc hai của 3 là số vô tỉ. Video này cung cấp lời giải chi tiết và dễ hiểu để thu hút người xem.
Bằng Chứng: Căn Bậc Hai Của 3 Là Số Vô Tỉ
READ MORE:
Khám phá bằng chứng toán học rằng căn bậc hai của 3 là số vô tỉ. Video này cung cấp lời giải chi tiết và dễ hiểu để thu hút người xem.
Bằng Chứng Rằng Căn Bậc Hai Của 3 Là Số Vô Tỉ