Topic cube root of 320: Discover how to easily calculate and understand the cube root of 320. This guide breaks down the steps, offers tips for accurate approximations, and explains the concept in simple terms. Whether you're a student or just curious, this article provides everything you need to master the cube root of 320.
Table of Content
- Cube Root of 320
- Introduction to Cube Roots
- Understanding the Concept of Cube Roots
- Methods to Calculate Cube Roots
- Calculating the Cube Root of 320
- Approximation Techniques for Cube Roots
- Using Calculators for Cube Root Calculation
- Manual Calculation Steps for Cube Roots
- Applications of Cube Roots in Real Life
- Common Mistakes in Calculating Cube Roots
- FAQs on Cube Roots
- Additional Resources and Tools for Cube Roots
- YOUTUBE:
Cube Root of 320
The cube root of a number is a value that, when multiplied by itself three times, gives the original number. In mathematical notation, the cube root of 320 is represented as \(\sqrt[3]{320}\).
Calculation
The cube root of 320 can be approximated using a calculator or through estimation methods. Using a calculator, the cube root of 320 is approximately:
\(\sqrt[3]{320} \approx 6.828\)
Steps for Estimation
- Identify the perfect cubes closest to 320. These are \(216\) (\(6^3\)) and \(343\) (\(7^3\)).
- Since 320 is closer to 343, we know the cube root of 320 is slightly less than 7.
- Using a calculator or more precise methods, we refine this estimate to approximately 6.828.
Properties of Cube Roots
- The cube root of a positive number is positive.
- The cube root of a negative number is negative.
- Cube roots are not necessarily integers unless the original number is a perfect cube.
| Original Number | Cube Root |
| 320 | \(\sqrt[3]{320} \approx 6.828\) |
Thus, the cube root of 320 is approximately 6.828.

READ MORE:
Introduction to Cube Roots
The cube root of a number is a value that, when multiplied by itself three times, equals the original number. It is represented mathematically as \(\sqrt[3]{x}\). Understanding cube roots is essential in various mathematical applications, including geometry, algebra, and real-life problem-solving scenarios.
Here are some key points to help you understand cube roots better:
- Definition: If \( y \) is the cube root of \( x \), then \( y^3 = x \).
- Symbol: The cube root of a number \( x \) is denoted as
\(\sqrt[3]{x}\). - Examples:
- The cube root of 27 is 3, because \( 3^3 = 27 \).
- The cube root of 8 is 2, because \( 2^3 = 8 \).
- The cube root of 64 is 4, because \( 4^3 = 64 \).
- Properties:
- Cube roots can be positive or negative.
- Every real number has one real cube root.
- Cube roots of negative numbers are also negative, e.g., \( \sqrt[3]{-8} = -2 \).
Calculating the cube root can be done using several methods:
- Using a Calculator: Most scientific calculators have a cube root function.
- Manual Estimation: Identify the nearest perfect cubes and estimate the value.
- Prime Factorization: Break down the number into prime factors and simplify.
For example, to find the cube root of 320, you can use a calculator to get an approximate value:
\(\sqrt[3]{320} \approx 6.828\)
Understanding and calculating cube roots can significantly enhance your mathematical skills and help solve complex problems more efficiently.
Understanding the Concept of Cube Roots
The cube root of a number is a special value that, when multiplied by itself twice more, results in the original number. It is denoted by the radical symbol with a small three above it, \(\sqrt[3]{x}\), or written as \(x^{\frac{1}{3}}\).
To fully grasp the concept of cube roots, consider the following points:
- Definition: The cube root of \(x\) is a number \(y\) such that \(y^3 = x\). For example, the cube root of 8 is 2 because \(2^3 = 8\).
- Notation: Cube roots are represented as
\(\sqrt[3]{x}\)or \(x^{\frac{1}{3}}\). - Calculation:
- Identify the perfect cubes around the given number. For 320, these are \(216\) (since \(6^3\)) and \(343\) (since \(7^3\)).
- Since 320 is between 216 and 343, the cube root of 320 is between 6 and 7.
- Using a calculator or more precise methods, the cube root of 320 is approximately 6.828.
- Properties of Cube Roots:
- Every real number has exactly one real cube root.
- The cube root of a positive number is positive.
- The cube root of a negative number is negative. For example, \(\sqrt[3]{-8} = -2\) because \((-2)^3 = -8\).
- Cube roots are not necessarily integers unless the original number is a perfect cube.
Here is a quick reference table for some common cube roots:
| Number | Cube Root |
| 8 | 2 |
| 27 | 3 |
| 64 | 4 |
| 125 | 5 |
| 216 | 6 |
Understanding cube roots allows for solving various mathematical problems and applications in science and engineering, enhancing overall numerical literacy and problem-solving skills.
Methods to Calculate Cube Roots
Calculating the cube root of a number can be done using several different methods, each with its own advantages. Below, we explore the most common methods to find the cube root of 320:
- Using a Calculator:
- Turn on the scientific calculator.
- Enter the number 320.
- Press the cube root button (often labeled as
\(\sqrt[3]{x}\)or similar). - Read the result, which should be approximately 6.828.
- Prime Factorization Method:
- Express the number as a product of prime factors. For 320, the factorization is \(320 = 2^6 \times 5\).
- Group the factors into triples, if possible. Here, it can be grouped as \( (2^3)^2 \times \sqrt[3]{5} \).
- Take the cube root of each group: \( \sqrt[3]{2^6} = 2^2 = 4 \) and multiply by \( \sqrt[3]{5} \).
- Since \( \sqrt[3]{5} \approx 1.710 \), the approximate result is \( 4 \times 1.710 = 6.84 \).
- Estimation Method:
- Identify the perfect cubes closest to 320. These are \(216\) (\(6^3\)) and \(343\) (\(7^3\)).
- Since 320 is between 216 and 343, estimate that the cube root is between 6 and 7.
- Refine the estimate by averaging or using interpolation. Here, 320 is closer to 343, so the cube root is slightly less than 7.
- Use a more precise method or calculator to find that \(\sqrt[3]{320} \approx 6.828\).
- Newton's Method (Iterative Approximation):
- Choose an initial guess. For 320, start with \(x_0 = 6\).
- Apply the formula \( x_{n+1} = \frac{1}{3} \left( 2x_n + \frac{320}{x_n^2} \right) \).
- Repeat the process until the value converges to a stable number. After a few iterations, the result will be close to 6.828.
Each of these methods provides a way to calculate cube roots, depending on the tools and precision required. For most practical purposes, using a calculator or estimation method is sufficient, while Newton's Method offers high precision for more demanding applications.
Calculating the Cube Root of 320
The cube root of 320 can be calculated using several methods, each providing a different level of precision and understanding. Below, we explore the step-by-step process for various calculation methods:
- Using a Calculator:
- Turn on your scientific calculator.
- Enter the number 320.
- Press the cube root button (often labeled as
\(\sqrt[3]{x}\)or similar). - The display will show the result, which is approximately 6.828.
- Prime Factorization Method:
- Express 320 as a product of prime factors: \(320 = 2^6 \times 5\).
- Group the factors into sets of three: \((2^3)^2 \times \sqrt[3]{5}\).
- Take the cube root of each group: \(\sqrt[3]{2^6} = 2^2 = 4\) and \(\sqrt[3]{5} \approx 1.710\).
- Multiply these results: \(4 \times 1.710 \approx 6.84\).
- Estimation Method:
- Identify the perfect cubes nearest to 320: 216 (\(6^3\)) and 343 (\(7^3\)).
- Since 320 is between 216 and 343, the cube root is between 6 and 7.
- Refine the estimate using interpolation. Given 320 is closer to 343, the cube root is slightly less than 7.
- Using a calculator, you find \(\sqrt[3]{320} \approx 6.828\).
- Newton's Method (Iterative Approximation):
- Choose an initial guess, \(x_0\). For 320, start with 6.
- Apply the iterative formula: \(x_{n+1} = \frac{1}{3} \left(2x_n + \frac{320}{x_n^2}\right)\).
- Repeat the process until the value converges. After a few iterations, the result will stabilize around 6.828.
For example, using Newton's Method:
- Starting with \(x_0 = 6\)
- First iteration: \(x_1 = \frac{1}{3} \left(2 \cdot 6 + \frac{320}{6^2}\right) \approx 6.481\)
- Second iteration: \(x_2 = \frac{1}{3} \left(2 \cdot 6.481 + \frac{320}{6.481^2}\right) \approx 6.842\)
- Third iteration: \(x_3 = \frac{1}{3} \left(2 \cdot 6.842 + \frac{320}{6.842^2}\right) \approx 6.828\)
Thus, using different methods, you can accurately determine that the cube root of 320 is approximately 6.828.

Approximation Techniques for Cube Roots
Approximation techniques are useful for finding cube roots when exact calculation methods are not available. These techniques provide a way to estimate the cube root of a number, such as 320, with reasonable accuracy. Here are some effective approximation methods:
- Estimation by Perfect Cubes:
- Identify the perfect cubes around the number. For 320, the closest perfect cubes are 216 (\(6^3\)) and 343 (\(7^3\)).
- Since 320 is between 216 and 343, its cube root will be between 6 and 7.
- Refine the estimate by considering how close 320 is to 216 and 343. Since it is closer to 343, the cube root is slightly less than 7.
- Using interpolation, you can approximate: \(\sqrt[3]{320} \approx 6.8\).
- Using Linear Interpolation:
- Set up the proportion based on the known cube roots. For example, between \(6^3\) and \(7^3\): \((320 - 216) / (343 - 216)\).
- Calculate the fraction: \((320 - 216) = 104\) and \((343 - 216) = 127\).
- The ratio is \(104 / 127 \approx 0.819\).
- Add this ratio to the lower cube root (6): \(6 + 0.819 = 6.819\).
- Thus, \(\sqrt[3]{320} \approx 6.819\).
- Newton's Method (Iterative Approximation):
- Choose an initial guess, \(x_0\). For 320, start with 6.
- Apply the iterative formula: \(x_{n+1} = \frac{1}{3} \left(2x_n + \frac{320}{x_n^2}\right)\).
- Repeat the process until the value converges.
- First iteration: \(x_1 = \frac{1}{3} \left(2 \cdot 6 + \frac{320}{6^2}\right) \approx 6.481\).
- Second iteration: \(x_2 = \frac{1}{3} \left(2 \cdot 6.481 + \frac{320}{6.481^2}\right) \approx 6.842\).
- Third iteration: \(x_3 = \frac{1}{3} \left(2 \cdot 6.842 + \frac{320}{6.842^2}\right) \approx 6.828\).
- Graphical Method:
- Plot the function \(y = x^3\) and \(y = 320\) on a graph.
- Identify the point where the curve \(y = x^3\) intersects the line \(y = 320\).
- The x-coordinate of this intersection point gives the approximate cube root of 320.
- By examining the graph, you can estimate that \(\sqrt[3]{320} \approx 6.8\).
Using these approximation techniques, one can find that the cube root of 320 is approximately 6.828. These methods provide a practical approach for estimating cube roots when precision tools are not available.
Using Calculators for Cube Root Calculation
Calculators provide a quick and accurate way to determine the cube root of a number. Here, we will detail the steps to calculate the cube root of 320 using different types of calculators, including scientific calculators, online calculators, and calculator apps.
- Using a Scientific Calculator:
- Turn on the scientific calculator.
- Enter the number 320.
- Locate the cube root function, often labeled as
\(\sqrt[3]{x}\)or \(\text{y-root}\). - Press the cube root button.
- The display will show the result, approximately 6.828.
- Using an Online Calculator:
- Open your web browser and navigate to a reliable online calculator website.
- Find the cube root function, usually in the advanced or scientific section.
- Enter the number 320 in the input field.
- Click the calculate or equal button to obtain the result.
- The website will display the cube root of 320, which is approximately 6.828.
- Using a Calculator App:
- Open the calculator app on your smartphone or tablet.
- Switch to the scientific mode if the app is in standard mode.
- Input the number 320.
- Press the cube root function button, usually labeled as
\(\sqrt[3]{x}\)or similar. - The app will display the result, approximately 6.828.
In addition to these methods, many modern calculators and apps offer additional features such as history logs, allowing you to keep track of your calculations. This can be particularly useful for students and professionals who need to perform multiple calculations. Using calculators for cube root calculations ensures accuracy and saves time, making it a preferred method for both simple and complex mathematical tasks.
Manual Calculation Steps for Cube Roots
Manually calculating the cube root of a number can be done through an iterative approximation method. Here's a detailed step-by-step process to find the cube root of 320:
-
Initial Approximation:
Start with an initial guess. For 320, a reasonable guess is 6 because \(6^3 = 216\) and \(7^3 = 343\).
-
Refine the Approximation:
Use the formula:
Here, \(a = 320\) and \(x_n\) is the current approximation. -
Iterative Calculation:
-
First Iteration:
Simplifying this:
-
Second Iteration:
Simplifying this further will get us closer to the actual cube root.
-
-
Repeat:
Continue refining the approximation until the desired accuracy is achieved.
This iterative process converges to the cube root of 320, which is approximately 6.8399.
Applications of Cube Roots in Real Life
Cube roots have numerous practical applications in various fields, helping to solve real-world problems. Here are some key applications:
-
Calculating Dimensions of Cubic Objects:
When the volume of a cubic object is known, the cube root helps in finding the dimensions. For example, if a storage box has a volume of 320 cubic units, the side length of the box can be found by taking the cube root of 320.
-
Volume Calculation of Containers:
Cube roots are used to determine the dimensions of containers such as tanks and crates. For instance, knowing the volume of a water tank allows for calculating the side length, which is crucial for design and construction.
-
Nanotechnology:
In nanotechnology, precise control over nanoparticle sizes is essential. By finding the cube root of the volume of a nanoparticle, scientists can determine its dimensions, which is critical in research and development of nanomaterials.
-
Material Strength Enhancement:
Engineers use cube roots to incise cubic shapes into materials like cast iron to improve their tensile strength. The cube root helps in controlling the quantity and dimensions of the added material.
-
Estimating Construction Materials:
In construction, cube roots are used to estimate the amount of material required. For example, calculating the side length of a cubic tower's volume helps determine the necessary building materials.
-
Tile Installation:
Cube roots assist in estimating the number of tiles needed to cover a floor. By determining the side length of a cubic room from its volume, the area of the floor can be calculated, leading to an accurate estimate of tile quantity.
These applications highlight the significance of cube roots in simplifying and solving complex real-life problems, making them an invaluable mathematical tool.

Common Mistakes in Calculating Cube Roots
Calculating cube roots can be tricky, and there are several common mistakes that students and professionals often make. Here are some of the most frequent errors and how to avoid them:
- Forgetting the Properties of Cube Roots: Remember that the cube root of a negative number is also negative, and the cube root of a positive number is positive. For example, \(\sqrt[3]{-27} = -3\) and \(\sqrt[3]{27} = 3\).
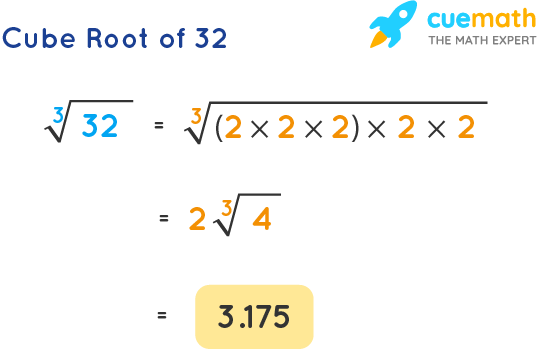
- Incorrectly Simplifying Radicals: When simplifying cube roots, it's essential to correctly identify and extract perfect cubes from the number. For instance, in \(\sqrt[3]{320}\), identify the largest perfect cube (64) and simplify to \(4\sqrt[3]{5}\).
- Misapplying the Cube Root Formula: The cube root of a number \(x\) is written as \(x^{1/3}\). Ensure correct application in calculations, such as \(\sqrt[3]{x} = x^{1/3}\).
- Boundary and Estimation Errors: When manually calculating cube roots by interval halving, ensure you accurately update and halve the interval. For example, to estimate \(\sqrt[3]{10}\), start with boundaries (2 and 3), then iterate by halving until the desired accuracy is reached.
- Neglecting Significance of Decimal Places: For precise calculations, especially in real-life applications, ensure you carry enough decimal places to avoid rounding errors. For instance, \(\sqrt[3]{320} \approx 6.8399\).
- Misunderstanding Properties of Irrational Numbers: Cube roots of non-perfect cubes are often irrational. For example, \(\sqrt[3]{320}\) cannot be exactly expressed as a simple fraction.
- Using Incorrect Units in Real-World Applications: Always match units when applying cube roots in problems involving volume, density, or other physical properties. For example, if the volume of a cube is given in cubic meters, the resulting side length will be in meters.
By being aware of these common mistakes and taking steps to avoid them, you can improve your accuracy and confidence in calculating cube roots.
FAQs on Cube Roots
Below are some frequently asked questions regarding cube roots:
-
What is the cube root of a negative number?
The cube root of a negative number is also a negative number. For example, the cube root of -8 is -2, because -2 × -2 × -2 = -8.
-
Can every number have a cube root?
Yes, every real number has a unique cube root. However, complex numbers may have multiple cube roots.
-
How can I calculate the cube root without a calculator?
You can calculate the cube root using the long division method or by using an approximation method using a table of cube roots.
-
How can I simplify a cube root?
You can simplify a cube root by factoring the number inside the cube root into its prime factors and then taking out the factors that appear in groups of three. For example, ∛24 can be simplified as ∛8 × ∛3, which is equal to 2∛3.
-
What is the relationship between square roots and cube roots?
Square roots and cube roots are both types of roots, but square roots find the number that when multiplied by itself once gives the original number, while cube roots find the number that when multiplied by itself twice (cubed) gives the original number.
-
Is the cube root of 320 a rational number?
No, the cube root of 320 is an irrational number because it cannot be expressed as a fraction of two integers. Its approximate value is 6.8399.
-
What are some real-life applications of cube roots?
Cube roots are used in various fields such as engineering, physics, and computer graphics to calculate volumes, solve equations involving cubic functions, and model natural phenomena.
-
How can I approximate the cube root of a number?
You can use estimation techniques, such as finding nearby perfect cubes and interpolating between them. For example, since 320 is between 216 (6^3) and 343 (7^3), the cube root of 320 is between 6 and 7.
Additional Resources and Tools for Cube Roots
Understanding and calculating cube roots can be made easier with the use of various resources and tools. Here are some helpful options:
-
Online Calculators: Numerous online calculators are available to compute cube roots quickly and accurately. For instance, offers a simple tool for finding the cube root of any number.
-
Educational Websites: Websites like provide detailed explanations, examples, and step-by-step guides for understanding cube roots. They also offer interactive math programs and problem-solving sessions.
-
Mathematics Software: Tools like WolframAlpha can handle complex cube root calculations and provide detailed solutions and visual representations. These platforms are excellent for more advanced mathematical analysis.
-
Prime Factorization Tools: For a more manual approach, tools that help with prime factorization can assist in simplifying cube roots. These tools break down numbers into their prime factors, which can then be grouped to find cube roots.
-
Educational Videos: Platforms like Khan Academy and YouTube host numerous videos explaining the concept of cube roots, their properties, and how to calculate them both manually and using technology.
-
Worksheets and Practice Problems: Practice is key to mastering cube roots. Websites such as MathisFun and various math tutoring services offer worksheets and problem sets to reinforce learning.
-
Mobile Apps: Several mobile apps are designed to help students and enthusiasts practice and understand cube roots on the go. Apps like Photomath allow users to take pictures of math problems and get instant solutions.
Using these resources can significantly enhance your understanding and ability to calculate cube roots effectively.
Tìm Giá Trị của 2*căn bậc ba của 40+3*căn bậc ba của 625-4*căn bậc ba của 320
READ MORE:
Đơn Giản Hóa 2 Căn Bậc 3 Của 40 + 3 Căn Bậc 3 Của 625 - 4 Căn Bậc 3 Của 320