Topic 3 square root 6: Delve into the intriguing world of mathematics as we explore the expression 3 square root 6. Discover its properties, applications in various fields, and step-by-step methods to calculate and simplify it. This comprehensive guide is designed to enhance your understanding and appreciation of this fascinating mathematical concept.
Table of Content
- Understanding the Expression \(3 \sqrt{6}\)
- Introduction to Square Roots
- Understanding the Expression 3 Square Root 6
- Mathematical Properties of Square Roots
- Calculating Square Roots
- Simplifying Expressions with Square Roots
- Applications of Square Roots in Various Fields
- Geometric Applications of 3 Square Root 6
- Algebraic Applications of 3 Square Root 6
- Physical Applications of 3 Square Root 6
- Step-by-Step Guide to Calculating 3 Square Root 6
- Common Mistakes in Simplifying Square Root Expressions
- Advanced Concepts Involving Square Roots
- Practical Examples and Exercises
- Conclusion: Importance of Understanding Square Root Expressions
- YOUTUBE: Xem video này để hiểu về khái niệm gốc bình phương và các ứng dụng trong toán học. Hướng dẫn chi tiết và dễ hiểu.
Understanding the Expression \(3 \sqrt{6}\)
The expression \(3 \sqrt{6}\) represents a mathematical term where the number 3 is multiplied by the square root of 6. This can be useful in various mathematical calculations, including algebra, geometry, and more advanced fields.
Breaking Down the Expression
- The square root of 6 (\(\sqrt{6}\)) is an irrational number, approximately equal to 2.449.
- When multiplied by 3, the expression \(3 \sqrt{6}\) simplifies to approximately 7.348.
Applications of \(3 \sqrt{6}\)
This expression can be found in various mathematical contexts:
- Geometry: It might be used in calculations involving areas or volumes, especially in problems related to triangular or rectangular shapes.
- Physics: The expression could appear in formulas related to waves, vibrations, or other physical phenomena.
- Algebra: It may be part of algebraic equations that require simplification or solving for variables.
Calculating \(3 \sqrt{6}\)
| Expression | Approximate Value |
| \(\sqrt{6}\) | 2.449 |
| \(3 \times \sqrt{6}\) | 7.348 |
By understanding and calculating expressions like \(3 \sqrt{6}\), students and professionals can solve complex mathematical problems more effectively. Practice with such expressions enhances computational skills and mathematical reasoning.

READ MORE:
Introduction to Square Roots
Square roots are fundamental mathematical operations that are crucial in various fields of mathematics and science. Understanding square roots involves recognizing their properties and how they interact with other mathematical expressions. Here, we provide a detailed introduction to square roots, focusing on their definition, properties, and examples.
Definition of Square Roots
The square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). It is denoted as \( \sqrt{x} \). For example, the square root of 9 is 3 because \( 3 \times 3 = 9 \).
Properties of Square Roots
- Non-negative: The square root of a non-negative number is always non-negative.
- Multiplication: The square root of a product is the product of the square roots: \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \).
- Division: The square root of a quotient is the quotient of the square roots: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
- Rational and Irrational: The square root of a perfect square is rational, while the square root of a non-perfect square is irrational.
Examples of Square Roots
| Number | Square Root |
| 4 | \( \sqrt{4} = 2 \) |
| 16 | \( \sqrt{16} = 4 \) |
| 25 | \( \sqrt{25} = 5 \) |
| Non-perfect square: 6 | \( \sqrt{6} \approx 2.449 \) |
Importance of Square Roots
Square roots are essential in solving quadratic equations, analyzing geometric shapes, and understanding physical phenomena. Mastery of square roots enhances problem-solving skills and mathematical comprehension, forming a foundation for more advanced mathematical concepts.
Understanding the Expression 3 Square Root 6
The expression \(3 \sqrt{6}\) combines a constant multiplier with a square root, resulting in a unique mathematical value. This section will break down the components of the expression and explain how to work with it effectively.
Components of the Expression
- Constant Multiplier: The number 3 is a constant multiplier in the expression.
- Square Root: The square root of 6, denoted as \( \sqrt{6} \), is an irrational number approximately equal to 2.449.
Step-by-Step Calculation
To understand and calculate \(3 \sqrt{6}\), follow these steps:
- Calculate the Square Root: First, find the approximate value of \( \sqrt{6} \):
- \( \sqrt{6} \approx 2.449 \)
- Multiply by 3: Next, multiply this value by 3:
- \( 3 \times 2.449 = 7.347 \)
Simplifying the Expression
While \(3 \sqrt{6}\) is already in a simplified form, it's essential to understand its approximate decimal value for practical applications. The expression remains \(3 \sqrt{6}\) in symbolic calculations, but for numerical approximations, it is around 7.347.
Applications of \(3 \sqrt{6}\)
- Geometry: It can be used to calculate lengths, areas, and volumes in geometric problems.
- Algebra: Often appears in algebraic equations and simplifications.
- Physics: May be used in formulas to describe physical phenomena such as wave functions or energy levels.
Example Problems
| Problem | Solution |
| Find the length of the hypotenuse of a right triangle with legs of 3 and \( \sqrt{6} \). | \( \sqrt{3^2 + (\sqrt{6})^2} = \sqrt{9 + 6} = \sqrt{15} \approx 3.873 \) |
| Simplify \(3 \sqrt{6} \times 2\). | \(6 \sqrt{6} \approx 6 \times 2.449 = 14.694 \) |
By thoroughly understanding and working with the expression \(3 \sqrt{6}\), one can enhance their mathematical proficiency and apply this knowledge to a variety of mathematical and real-world problems.
Mathematical Properties of Square Roots
The square root is a fundamental concept in mathematics with several important properties that are useful in various applications. Below are the key mathematical properties of square roots:
- Definition: The square root of a number \( x \) is a value that, when multiplied by itself, gives the number \( x \). It is denoted as \( \sqrt{x} \).
- Non-Negativity: For any real number \( x \geq 0 \), the square root \( \sqrt{x} \) is always non-negative.
- Product Property: The square root of a product is the product of the square roots:
\[
\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}
\] - Quotient Property: The square root of a quotient is the quotient of the square roots:
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\] - Exponent Relation: The square root can be expressed as an exponent:
\[
\sqrt{x} = x^{\frac{1}{2}}
\] - Even and Odd Powers: For any non-negative number \( x \), the square root of \( x^2 \) is \( x \):
\[
For any real number \( x \), the principal square root of \( x^2 \) is the absolute value of \( x \):
\sqrt{x^2} = x
\]\[
\sqrt{x^2} = |x|
\]
These properties are essential for understanding and working with square roots in various mathematical contexts. Let's delve into some examples involving these properties to solidify our understanding:
Examples:
- Using the product property:
\[
\sqrt{36 \cdot 25} = \sqrt{36} \cdot \sqrt{25} = 6 \cdot 5 = 30
\] - Using the quotient property:
\[
\sqrt{\frac{49}{16}} = \frac{\sqrt{49}}{\sqrt{16}} = \frac{7}{4}
\] - Using the exponent relation:
\[
\sqrt{81} = 81^{\frac{1}{2}} = 9
\]
Understanding these properties allows for simplification and manipulation of expressions involving square roots, enabling their application in algebra, geometry, and various fields of science and engineering.
Calculating Square Roots
Calculating square roots involves finding a number that, when multiplied by itself, equals the given number. The square root of a number \( x \) is denoted as \( \sqrt{x} \). Here's a step-by-step guide to calculating square roots:
-
Using Prime Factorization:
- Prime factorize the number under the square root.
- Group the factors into pairs of the same number.
- Take one factor from each pair and multiply them together.
- If there are unpaired factors, multiply them under the square root sign.
Example: \( \sqrt{72} \)
- Prime factorization: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \)
- Group into pairs: \( (2 \times 2) \times 2 \times (3 \times 3) \)
- Extract pairs: \( 2 \times 3 \sqrt{2} = 6\sqrt{2} \)
-
Using Long Division Method:
- Separate the number into pairs of digits starting from the decimal point.
- Find the largest number whose square is less than or equal to the first pair. This is the first digit of the square root.
- Subtract the square of the first digit from the first pair and bring down the next pair.
- Double the current result and determine the next digit by trial and error.
- Repeat the process until all pairs are processed.
Example: \( \sqrt{529} \)
- Pairs: \( 5 | 29 \)
- First digit: \( 2 \) (since \( 2^2 = 4 \leq 5 \))
- Subtract and bring down: \( 5 - 4 = 1 \), bring down \( 29 \) → \( 129 \)
- Next digit: \( 3 \) (since \( (20 + 3) \times 3 = 123 \leq 129 \))
- Result: \( \sqrt{529} = 23 \)
-
Using a Calculator:
- Enter the number into the calculator.
- Press the square root button (usually denoted as \( \sqrt{} \)).
- Read the result displayed on the screen.
Using these methods, you can calculate the square root of any number. For non-perfect squares, the result will be an approximation. Practicing these techniques will help you become proficient in calculating square roots both manually and using technology.

Simplifying Expressions with Square Roots
Simplifying expressions involving square roots involves rewriting the expression in its simplest form. Here are detailed steps to simplify square root expressions, including the specific case of \( 3\sqrt{6} \):
-
Simplifying Square Roots:
- Factorize the number under the square root into its prime factors.
- Group the prime factors into pairs.
- Extract one factor from each pair outside the square root.
- Multiply the extracted factors together.
Example: \( \sqrt{72} \)
- Prime factorization: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \)
- Group into pairs: \( (2 \times 2) \times 2 \times (3 \times 3) \)
- Extract pairs: \( 2 \times 3 \sqrt{2} = 6\sqrt{2} \)
-
Simplifying Coefficients and Square Roots:
- Combine the coefficients outside the square root with the simplified square root value.
- If the expression has a coefficient outside the square root, multiply it with the simplified square root.
Example: \( 3\sqrt{8} \)
- Simplify \( \sqrt{8} \): \( \sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2} \)
- Combine: \( 3 \times 2\sqrt{2} = 6\sqrt{2} \)
-
Adding and Subtracting Square Roots:
- Ensure the terms under the square roots are the same.
- Add or subtract the coefficients of the like terms.
Example: \( 2\sqrt{3} + 5\sqrt{3} \)
- Like terms: \( \sqrt{3} \)
- Combine coefficients: \( 2 + 5 = 7 \)
- Result: \( 7\sqrt{3} \)
-
Multiplying Square Roots:
- Multiply the coefficients outside the square roots.
- Multiply the values inside the square roots together.
- Simplify the resulting square root if possible.
Example: \( (2\sqrt{3})(4\sqrt{6}) \)
- Multiply coefficients: \( 2 \times 4 = 8 \)
- Multiply inside the square roots: \( \sqrt{3 \times 6} = \sqrt{18} \)
- Simplify: \( \sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2} \)
- Combine: \( 8 \times 3\sqrt{2} = 24\sqrt{2} \)
By following these steps, you can simplify any expression involving square roots. For instance, \( 3\sqrt{6} \) is already in its simplest form because \( \sqrt{6} \) cannot be simplified further. Simplification techniques are essential for solving more complex mathematical problems efficiently.
Applications of Square Roots in Various Fields
Square roots are fundamental in various fields, providing essential tools for calculations and problem-solving. Below are some key applications:
-
Geometry:
Square roots are vital in geometry, particularly in calculating the lengths of sides in right triangles using the Pythagorean theorem. For example, if a right triangle has legs of lengths 3 and 6, the hypotenuse is calculated as \( \sqrt{3^2 + 6^2} = \sqrt{45} = 3\sqrt{5} \). This principle is also used to determine areas and perimeters of geometric shapes.
-
Physics:
In physics, square roots are used to determine quantities such as the time it takes for an object to fall under gravity. For instance, the time \( t \) (in seconds) for an object to fall from a height \( h \) (in feet) is given by \( t = \frac{\sqrt{h}}{4} \). This relationship helps in calculating free fall times and analyzing projectile motion.
-
Engineering:
Engineers use square roots to calculate the natural frequencies of structures. This is essential for understanding how buildings, bridges, and other structures will respond to various forces, such as wind or traffic. The natural frequency \( f \) is proportional to the square root of the stiffness \( k \) divided by the mass \( m \): \( f = \sqrt{\frac{k}{m}} \).
-
Finance:
In finance, square roots are used to calculate stock market volatility. The volatility \( \sigma \) is the square root of the variance \( \sigma^2 \) of stock returns. This measure helps investors understand the risk associated with different investments.
-
Statistics:
Square roots are essential in statistics for calculating standard deviation, a measure of data spread. The standard deviation \( \sigma \) is the square root of the variance, providing insight into how much individual data points differ from the mean.
-
Computer Science:
Square roots are used in algorithms for encryption, image processing, and graphics. For example, calculating the distance between two points in a 3D space involves the square root of the sum of the squares of the coordinate differences.
-
Navigation:
In navigation, square roots are used to calculate distances between points on the earth's surface. The formula for the distance \( D \) between two points \( (x_1, y_1) \) and \( (x_2, y_2) \) in a plane is \( D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \).
-
Photography:
The aperture of a camera lens is related to the square root of the f-number, which controls the amount of light entering the camera. The area of the aperture is proportional to the square of the f-number, affecting exposure and depth of field in photographs.
-
Cooking:
When scaling recipes, the amount of ingredients often needs to be adjusted using square roots to maintain the correct proportions. For example, if a recipe is doubled, the amount of spices might be increased by a factor of the square root of 2 to ensure balanced flavors.
Geometric Applications of 3 Square Root 6
The expression \(3\sqrt{6}\) frequently appears in various geometric contexts. Here are some detailed applications:
-
Triangle Heights and Areas:
In right triangles, expressions involving \(3\sqrt{6}\) can be used to determine the heights and areas. For example, consider a right triangle where one leg is \(3\sqrt{6}\) units long. Using the Pythagorean theorem, if the other leg is of length \(a\), the hypotenuse \(c\) can be calculated as:
\[ c = \sqrt{(3\sqrt{6})^2 + a^2} = \sqrt{54 + a^2} \]
-
Diagonals in Rectangles:
In a rectangle with sides \(3\sqrt{6}\) and \(b\), the diagonal \(d\) can be found using the Pythagorean theorem:
\[ d = \sqrt{(3\sqrt{6})^2 + b^2} = \sqrt{54 + b^2} \]
-
Regular Hexagons:
The distance from the center to a vertex (the radius of the circumscribed circle) in a regular hexagon with a side length of \(3\sqrt{6}\) is:
\[ r = 3\sqrt{6} \]
This helps in calculating the area of the hexagon as:
\[ \text{Area} = \frac{3\sqrt{3}}{2} (3\sqrt{6})^2 = \frac{3\sqrt{3}}{2} \times 54 = 81\sqrt{3} \]
-
Volume of Cylinders:
In a cylinder with a radius of \(3\sqrt{6}\) and height \(h\), the volume \(V\) is given by:
\[ V = \pi (3\sqrt{6})^2 h = 54\pi h \]
-
Coordinate Geometry:
In 3D space, the distance between points \((0, 0, 0)\) and \((3\sqrt{6}, 3\sqrt{6}, 3\sqrt{6})\) is calculated as:
\[ \text{Distance} = \sqrt{(3\sqrt{6})^2 + (3\sqrt{6})^2 + (3\sqrt{6})^2} = \sqrt{54 + 54 + 54} = \sqrt{162} = 9\sqrt{2} \]
Algebraic Applications of 3 Square Root 6
The expression \(3\sqrt{6}\) has various algebraic applications, especially in simplifying and solving equations. Here, we will explore how this expression can be used in different algebraic contexts.
1. Simplifying Algebraic Expressions
Simplifying expressions involving square roots often uses the product property of square roots: \(\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}\). Let's simplify \(3\sqrt{6} \times 2\sqrt{3}\):
- Multiply the coefficients: \(3 \times 2 = 6\)
- Multiply the square root terms: \(\sqrt{6} \times \sqrt{3} = \sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\)
- Combine the results: \(6 \times 3\sqrt{2} = 18\sqrt{2}\)
2. Solving Equations Involving Square Roots
When solving equations with square roots, isolating the square root term and then squaring both sides can help. For instance, consider the equation involving \(3\sqrt{6}\):
\(3\sqrt{6x} = 18\)
- Isolate the square root term: \(\sqrt{6x} = 6\)
- Square both sides: \(6x = 36\)
- Solve for \(x\): \(x = \frac{36}{6} = 6\)
3. Factoring Algebraic Expressions
Factoring expressions that include square roots can simplify them significantly. Consider the expression \((3\sqrt{6})^2 - 36\):
First, recognize it as a difference of squares: \((a^2 - b^2) = (a - b)(a + b)\), where \(a = 3\sqrt{6}\) and \(b = 6\).
- Express the difference: \((3\sqrt{6})^2 - 36 = 54 - 36\)
- Simplify the terms: \((3\sqrt{6} - 6)(3\sqrt{6} + 6)\)
4. Multiplying Square Root Expressions
Multiplying expressions with square roots involves using the distributive property and simplifying. For example, multiplying \(3\sqrt{6}\) with another square root term like \(4\sqrt{3}\):
- Distribute the terms: \(3\sqrt{6} \cdot 4\sqrt{3}\)
- Multiply coefficients: \(3 \times 4 = 12\)
- Use the product property of square roots: \(\sqrt{6} \times \sqrt{3} = \sqrt{18} = 3\sqrt{2}\)
- Combine: \(12 \times 3\sqrt{2} = 36\sqrt{2}\)
5. Solving Quadratic Equations
Square roots frequently appear in solutions to quadratic equations via the quadratic formula: \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\). When the discriminant \(b^2 - 4ac\) involves \(6\), expressions like \(3\sqrt{6}\) might appear in the solutions.
Consider the quadratic equation \(2x^2 - 12x + 18 = 0\):
- Calculate the discriminant: \(b^2 - 4ac = 144 - 144 = 0\)
- Apply the quadratic formula: \(x = \frac{12 \pm 0}{4} = 3\)
In summary, \(3\sqrt{6}\) is useful in various algebraic contexts, from simplifying expressions to solving equations. Mastering these applications enhances overall mathematical problem-solving skills.

Physical Applications of 3 Square Root 6
Square roots, including expressions like \(3\sqrt{6}\), have a variety of physical applications across different fields. Here are some key examples:
- Gravity and Free Fall: In physics, square roots are essential for calculating the time it takes for an object to fall from a certain height under the influence of gravity. The formula used is \( t = \frac{\sqrt{h}}{4} \), where \( h \) is the height in feet and \( t \) is the time in seconds. For example, if an object is dropped from a height of \( h = 144 \) feet, the time \( t \) to reach the ground is \( t = \frac{\sqrt{144}}{4} = 3 \) seconds.
- Distance Calculation: Square roots are used to find the distance between two points in both 2D and 3D spaces. The distance \( D \) between points \((x_1, y_1)\) and \((x_2, y_2)\) in a plane is given by:
\[ D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]This principle extends to 3D space as well:\[ D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \]These calculations are crucial in fields like physics, engineering, and computer graphics.
- Architecture and Engineering: Engineers use square roots to determine the natural frequency of structures like bridges and buildings. The natural frequency helps in predicting how a structure will respond to various loads, such as wind or traffic. For instance, the frequency \( f \) of a vibrating system can be calculated using:
\[ f = \frac{1}{2\pi} \sqrt{\frac{k}{m}} \]where \( k \) is the stiffness and \( m \) is the mass of the structure.
- Accident Investigations: In accident reconstruction, the speed of a vehicle before braking can be estimated from the length of skid marks using square root formulas. For example, if the skid mark length \( d \) is measured, the speed \( v \) can be found by:
\[ v = \sqrt{24d} \]This helps investigators determine the speed at which a vehicle was traveling prior to an accident.
Understanding and applying square roots, such as \(3\sqrt{6}\), in these contexts allow for accurate measurements and predictions in various physical scenarios.
Step-by-Step Guide to Calculating 3 Square Root 6
To calculate \(3 \sqrt{6}\), follow these steps:
-
Understand the Expression
The expression \(3 \sqrt{6}\) consists of a coefficient (3) multiplied by the square root of 6. Our goal is to calculate the value of this expression.
-
Calculate the Square Root of 6
Find the approximate value of \(\sqrt{6}\). Using a calculator or estimation methods, we find:
\(\sqrt{6} \approx 2.449\)
-
Multiply by the Coefficient
Multiply the coefficient (3) by the calculated square root of 6:
\(3 \times 2.449 \approx 7.347\)
The approximate value of \(3 \sqrt{6}\) is 7.347.
Manual Calculation Using Estimation
For a more detailed manual calculation, follow these steps:
-
Initial Estimate
Estimate the value of \(\sqrt{6}\). We know that 6 is between the perfect squares 4 and 9, so \(\sqrt{6}\) is between 2 and 3. Let's take a closer estimate:
\(\sqrt{6} \approx 2.5\)
-
Refine the Estimate
To refine our estimate, we can use the average method:
- Divide the number (6) by our estimate (2.5):
- Average the result with our estimate:
\( \frac{6}{2.5} = 2.4 \)
\( \frac{2.5 + 2.4}{2} = 2.45 \)
This gives a refined estimate: \(\sqrt{6} \approx 2.45\).
-
Repeat the Process
We can repeat the process to get an even more accurate result:
- Divide the number (6) by our refined estimate (2.45):
- Average the result with our refined estimate:
\( \frac{6}{2.45} \approx 2.448 \)
\( \frac{2.45 + 2.448}{2} \approx 2.449 \)
Thus, the refined manual estimate for \(\sqrt{6}\) is 2.449. Multiplying this by 3:
\(3 \times 2.449 \approx 7.347\)
So, the value of \(3 \sqrt{6}\) is approximately 7.347.
Common Mistakes in Simplifying Square Root Expressions
Simplifying square root expressions can often lead to mistakes. Here are some common errors and how to avoid them:
- Incorrect Application of the Product Rule: The product rule states that \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\). A common mistake is to apply this rule incorrectly. For example, \(\sqrt{12} \cdot \sqrt{3}\) should be simplified as \(\sqrt{12 \cdot 3} = \sqrt{36} = 6\), not \(\sqrt{12 + 3} = \sqrt{15}\).
- Failure to Factor Perfect Squares: Always factor out perfect squares from the radicand. For instance, \(\sqrt{50}\) should be simplified as \(\sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}\). Ignoring this step leads to incomplete simplification.
- Incorrect Simplification of Variables: When simplifying variables under a square root, remember that \(\sqrt{x^2} = x\) (assuming \(x\) is nonnegative). For example, \(\sqrt{x^4}\) simplifies to \(x^2\), not \(x^2 \sqrt{x^2}\).
- Errors in Rationalizing the Denominator: Rationalizing involves removing the square root from the denominator. For example, \(\frac{1}{\sqrt{2}}\) should be multiplied by \(\frac{\sqrt{2}}{\sqrt{2}}\) to get \(\frac{\sqrt{2}}{2}\). A mistake here would be to leave the expression as \(\frac{1}{\sqrt{2}}\).
- Confusing Addition and Multiplication of Radicals: The expression \(\sqrt{a} + \sqrt{b}\) cannot be simplified to \(\sqrt{a + b}\). For instance, \(\sqrt{2} + \sqrt{3}\) is not equal to \(\sqrt{5}\).
- Misapplication of the Quotient Rule: The quotient rule states that \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\). For example, \(\sqrt{\frac{9}{16}}\) should be simplified to \(\frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4}\). Incorrectly applying this rule might lead to incorrect results like \(\frac{\sqrt{9}}{16} = \frac{3}{16}\).
- Incorrect Simplification of Nested Radicals: Simplifying nested radicals like \(\sqrt{2 + \sqrt{3}}\) requires careful steps and often can't be simplified further without approximation. Avoid assuming such expressions can be easily simplified.
By understanding and avoiding these common mistakes, you can more accurately simplify square root expressions and apply them correctly in various mathematical contexts.
Advanced Concepts Involving Square Roots
Square roots are fundamental in mathematics and find application in various advanced concepts beyond basic arithmetic. Understanding the expression \( 3 \sqrt{6} \) involves delving into its properties and implications:
- Number Theory: \( 3 \sqrt{6} \) represents an irrational number, as it cannot be expressed as a simple fraction of integers. This characteristic makes it challenging to work with in exact terms but also highlights its unique mathematical nature.
- Algebraic Manipulations: When dealing with expressions like \( 3 \sqrt{6} \) in algebra, simplification involves rationalizing the denominator or using identities involving square roots to simplify complex equations.
- Geometric Interpretations: In geometry, \( 3 \sqrt{6} \) might represent the length of a diagonal in a rectangle whose sides are of certain lengths. This geometric application connects algebraic expressions with physical measurements.
- Trigonometric Context: Square roots play a crucial role in trigonometry, especially when dealing with right triangles and certain angles. \( 3 \sqrt{6} \) could relate to the side length of a triangle or be a component in trigonometric identities involving angles and ratios.
- Advanced Calculus: In calculus, square roots appear in the context of limits, derivatives, and integrals. \( 3 \sqrt{6} \) might appear as part of a function's derivative or in the evaluation of definite integrals where precise values are required.
- Complex Numbers: The square root symbol extends beyond real numbers into complex numbers, where \( 3 \sqrt{6} \) could be interpreted as part of an expression involving imaginary units. Understanding its placement in the complex plane aids in solving more intricate mathematical problems.
These advanced concepts demonstrate the versatility and importance of square roots in higher mathematics and their practical applications across different fields.
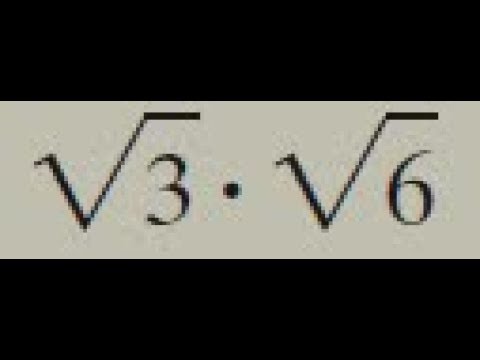
Practical Examples and Exercises
Understanding how to apply \( 3 \sqrt{6} \) in practical scenarios helps reinforce its mathematical significance. Here are some examples and exercises:
- Example 1: Geometry
Calculate the diagonal length of a rectangle with sides \( 3 \) units and \( \sqrt{6} \) units using the formula for the diagonal \( \sqrt{a^2 + b^2} \).
- Example 2: Trigonometry
Find the side length opposite a \( 75^\circ \) angle in a right triangle where the hypotenuse is \( 3 \sqrt{6} \) units long.
- Exercise 1: Algebraic Manipulation
Simplify the expression \( \frac{3 \sqrt{6}}{\sqrt{2}} \) by rationalizing the denominator.
- Exercise 2: Application in Physics
Determine the distance traveled by a particle moving with a velocity of \( 3 \sqrt{6} \) m/s for \( \sqrt{6} \) seconds.
- Exercise 3: Real-World Problem Solving
Calculate the amount of material required to construct a cylindrical tank with a diameter of \( 3 \sqrt{6} \) meters and a height of \( 2 \) meters.
Conclusion: Importance of Understanding Square Root Expressions
Mastering square root expressions such as \( 3 \sqrt{6} \) is crucial for several reasons:
- Foundation in Mathematics: Square roots are fundamental in arithmetic and algebra, forming the basis for more complex mathematical concepts.
- Real-World Applications: Understanding square roots helps in solving practical problems involving measurements, geometry, physics, and engineering.
- Advanced Mathematics: Square roots play a significant role in advanced mathematics such as calculus, number theory, and complex analysis.
- Problem-Solving Skills: Proficiency in handling square root expressions enhances problem-solving abilities, promoting logical thinking and analytical skills.
- Educational Advancement: Mastery of square roots is essential for progressing to higher levels of education and pursuing careers in STEM fields.
Therefore, comprehending \( 3 \sqrt{6} \) and similar expressions not only enriches mathematical knowledge but also opens doors to diverse academic and professional opportunities.
Xem video này để hiểu về khái niệm gốc bình phương và các ứng dụng trong toán học. Hướng dẫn chi tiết và dễ hiểu.
Gốc Bình Phương là Gì? | Toán học cùng Thầy J
READ MORE:
Xem video này để học cách đơn giản hóa các căn bậc hai trong toán học. Hướng dẫn chi tiết và dễ hiểu.
Cách Đơn Giản Hóa Căn Bậc Hai