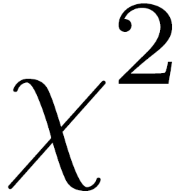Topic x squared equals: X squared equals a fundamental concept in algebra that opens the door to understanding quadratic equations, graphing parabolas, and solving real-world problems. Dive into the world of squared numbers to enhance your mathematical skills and explore practical applications in various fields, making complex problems simpler and more approachable.
Table of Content
- Understanding the Concept of Squaring
- Introduction to Squaring Numbers
- Basic Definition and Examples
- Pythagorean Theorem and Its Applications
- Factoring Techniques
- Trigonometric Identities Involving Squares
- Advanced Problem Solving
- Common Mistakes and How to Avoid Them
- Practical Applications in Various Fields
- Additional Resources for Learning
- YOUTUBE:
Understanding the Concept of Squaring
When we talk about the expression , we are referring to the operation where a number, variable, or expression is multiplied by itself. Let's delve into various aspects of this mathematical concept.
Basic Definition
The expression implies that x squared equals c. This means:
- If x = 3, then .
- If x = -4, then .
Solving Quadratic Equations
Quadratic equations often involve the squaring of a variable. A general form of a quadratic equation is . Solving such equations involves finding the values of x that satisfy the equation. Methods include:
- Factoring
- Using the quadratic formula:
- Completing the square
Graphing Quadratic Functions
Quadratic functions take the form . The graph of a quadratic function is a parabola. Key features include:
- The vertex, the highest or lowest point of the parabola
- The axis of symmetry, a vertical line that passes through the vertex
- The direction of opening (upwards if a > 0, downwards if a < 0)
Applications of Squaring
Squaring is fundamental in various fields such as physics, engineering, and computer science. Examples include:
- Calculating the area of a square: if the side length is x, the area is
- In kinematics, where displacement is squared in certain equations of motion
Resources for Further Learning
For more detailed explanations and practice problems, consider the following resources:
By understanding and mastering the concept of squaring, you can solve a wide range of mathematical problems and gain deeper insights into the subject.
READ MORE:
Introduction to Squaring Numbers
Squaring a number is one of the fundamental operations in mathematics. It involves multiplying a number by itself, and is often denoted as \( x^2 \). This operation is foundational in various fields such as algebra, geometry, and even in real-life applications like area calculation.
- Definition: \( x^2 \) means \( x \times x \).
- Examples:
- If \( x = 3 \), then \( x^2 = 3 \times 3 = 9 \).
- If \( x = -4 \), then \( x^2 = (-4) \times (-4) = 16 \).
- Properties of Squaring:
- Squaring a positive number yields a positive result.
- Squaring a negative number also yields a positive result.
- Zero squared is zero: \( 0^2 = 0 \).
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because they can be expressed as \( n^2 \), where \( n \) is an integer.
- Square Roots: The square root of \( x^2 \) is \( x \) or \( -x \). For example, \( \sqrt{25} = 5 \) or \( -5 \).
Understanding squaring is crucial as it leads to more complex topics like quadratic equations, where solutions often involve finding the square roots. Quadratic equations, which take the form \( ax^2 + bx + c = 0 \), are solved using methods like factoring, completing the square, or using the quadratic formula.
Basic Definition and Examples
The expression "x squared" means multiplying the variable x by itself, which is written mathematically as \( x^2 \). This operation is fundamental in algebra and geometry, often encountered in various mathematical problems and real-world applications.
Let's delve into some examples to illustrate the concept of squaring numbers:
- If \( x = 3 \), then \( x^2 = 3 \times 3 = 9 \).
- If \( x = -4 \), then \( x^2 = (-4) \times (-4) = 16 \).
- If \( x = 0.5 \), then \( x^2 = 0.5 \times 0.5 = 0.25 \).
In general, squaring a number results in a non-negative value. For any real number x, \( x^2 \geq 0 \). This is because both positive and negative numbers, when squared, yield positive results.
Additionally, the concept of perfect squares is closely related to squaring numbers. A perfect square is a number that can be expressed as the square of an integer. For instance:
- \( 1^2 = 1 \)
- \( 2^2 = 4 \)
- \( 3^2 = 9 \)
- \( 4^2 = 16 \)
- \( 5^2 = 25 \)
Squaring numbers also plays a crucial role in solving quadratic equations of the form \( ax^2 + bx + c = 0 \). Here, the term \( x^2 \) signifies the quadratic nature of the equation, and solving it involves finding the values of x that satisfy the equation. Techniques such as factoring, completing the square, and using the quadratic formula are commonly employed to find the roots of these equations.
Let's consider a basic quadratic equation:
\( x^2 - 5x + 6 = 0 \)
To solve this, we can factorize it as:
\( (x - 2)(x - 3) = 0 \)
This gives us the solutions \( x = 2 \) and \( x = 3 \). Thus, \( x^2 = 4 \) or \( x^2 = 9 \), depending on the value of x.
In conclusion, understanding the concept of squaring numbers is essential for mastering algebra and solving quadratic equations effectively. It is a fundamental mathematical operation that has wide-ranging applications in various fields.
Pythagorean Theorem and Its Applications
The Pythagorean Theorem is a fundamental principle in geometry, discovered by the ancient Greek mathematician Pythagoras. It states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This relationship can be expressed with the formula:
\[ a^2 + b^2 = c^2 \]
Where \( a \) and \( b \) are the lengths of the legs of the triangle, and \( c \) is the length of the hypotenuse.
Example Calculations
- For a triangle with legs of lengths 3 and 4 units, the hypotenuse can be found as follows:
- In another example, if the hypotenuse is 13 units and one leg is 5 units, the length of the other leg can be calculated:
\[
3^2 + 4^2 = 9 + 16 = 25 \implies c = \sqrt{25} = 5
\]
\[
5^2 + b^2 = 13^2 \implies 25 + b^2 = 169 \implies b^2 = 144 \implies b = \sqrt{144} = 12
\]
Applications of the Pythagorean Theorem
The Pythagorean Theorem is widely used in various real-world applications such as:
- Construction: To ensure buildings have right angles and to determine lengths of diagonals.
- Navigation: Calculating the shortest path between two points in navigation and cartography.
- Physics: Analyzing vector components in mechanics and electromagnetism.
- Computer Graphics: Calculating distances between points in 3D space.
These applications demonstrate the theorem's importance beyond theoretical mathematics, highlighting its practical utility in everyday problem-solving.
Factoring Techniques
Factoring is a fundamental technique used to simplify quadratic equations and other algebraic expressions. Here, we explore various methods to factor quadratic equations effectively.
Basic Factoring Method
To factor a quadratic equation in the standard form \(ax^2 + bx + c = 0\), follow these steps:
- Ensure the equation is in standard form.
- Identify two numbers that multiply to \(ac\) and add to \(b\).
- Rewrite the middle term \(bx\) using the identified numbers.
- Group the terms and factor out the greatest common factor (GCF) from each group.
- Write the factored form as a product of binomials.
Example 1: Simple Quadratic
Consider the quadratic equation \(x^2 + 5x + 6 = 0\). To factor:
- Find two numbers that multiply to \(6\) and add to \(5\). These numbers are \(2\) and \(3\).
- Rewrite the equation: \(x^2 + 2x + 3x + 6 = 0\).
- Group terms: \((x^2 + 2x) + (3x + 6) = 0\).
- Factor out the GCF from each group: \(x(x + 2) + 3(x + 2) = 0\).
- Write the factors: \((x + 2)(x + 3) = 0\).
Setting each factor to zero gives the solutions: \(x = -2\) and \(x = -3\).
Factoring When Leading Coefficient is Not 1
When the leading coefficient \(a \neq 1\), the process includes finding numbers that multiply to \(ac\) and add to \(b\). For example:
Solve \(2x^2 + 7x + 3 = 0\):
- Multiply \(a\) and \(c\) to get \(6\).
- Find two numbers that multiply to \(6\) and add to \(7\): \(1\) and \(6\).
- Rewrite the middle term: \(2x^2 + x + 6x + 3 = 0\).
- Group and factor: \(x(2x + 1) + 3(2x + 1) = 0\).
- Write the factors: \((2x + 1)(x + 3) = 0\).
Setting each factor to zero gives the solutions: \(x = -\frac{1}{2}\) and \(x = -3\).
Special Factoring Formulas
There are specific formulas for certain types of quadratic equations:
- Difference of Squares: \(a^2 - b^2 = (a - b)(a + b)\)
- Perfect Square Trinomials: \(a^2 + 2ab + b^2 = (a + b)^2\)
These special cases simplify factoring when the equation fits the pattern.
Example 2: Difference of Squares
Factor \(x^2 - 16 = 0\):
- Recognize it as a difference of squares: \(x^2 - 4^2\).
- Apply the formula: \((x - 4)(x + 4) = 0\).
Solutions are \(x = 4\) and \(x = -4\).
Example 3: Perfect Square Trinomial
Factor \(x^2 + 6x + 9 = 0\):
- Recognize it as a perfect square trinomial: \((x + 3)^2 = 0\).
The solution is \(x = -3\).
Understanding these factoring techniques enables solving quadratic equations and simplifying expressions efficiently.
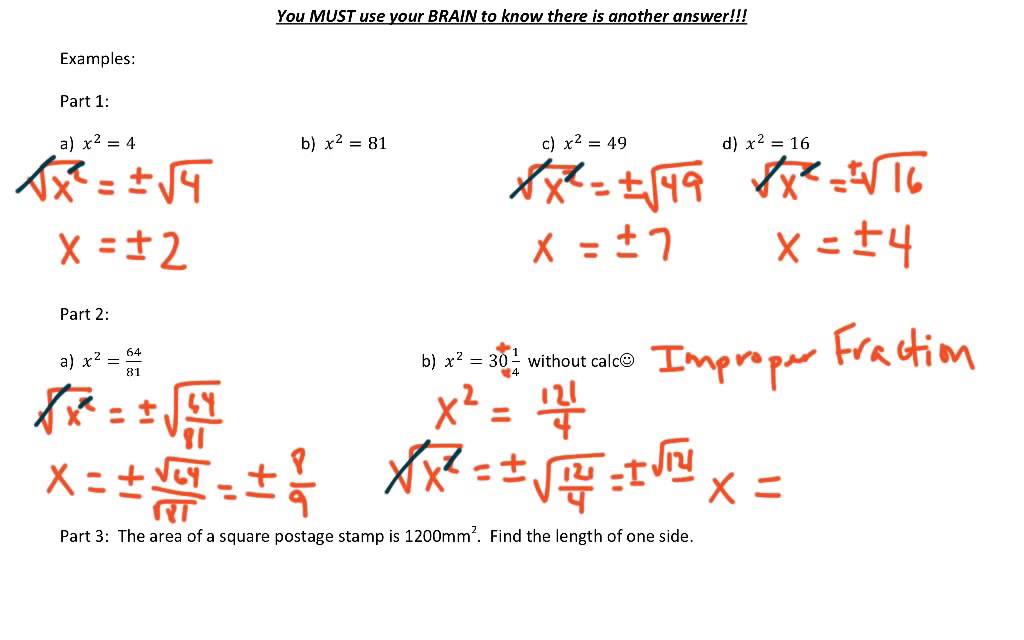
Trigonometric Identities Involving Squares
Trigonometric identities involving squares are fundamental in trigonometry and are used to simplify expressions and solve equations. Here, we cover some of the most essential identities:
Pythagorean Identities
The Pythagorean identities are derived from the Pythagorean theorem and are crucial in trigonometry:
\(\sin^2 \theta + \cos^2 \theta = 1\) \(1 + \tan^2 \theta = \sec^2 \theta\) \(1 + \cot^2 \theta = \csc^2 \theta\)
Double Angle Identities
Double angle identities express trigonometric functions of twice an angle in terms of functions of the original angle:
\(\sin 2\theta = 2\sin \theta \cos \theta\) \(\cos 2\theta = \cos^2 \theta - \sin^2 \theta = 2\cos^2 \theta - 1 = 1 - 2\sin^2 \theta\) \(\tan 2\theta = \frac{2\tan \theta}{1 - \tan^2 \theta}\)
Half Angle Identities
Half angle identities allow us to find the value of trigonometric functions at half an angle:
\(\sin \frac{\theta}{2} = \pm \sqrt{\frac{1 - \cos \theta}{2}}\) \(\cos \frac{\theta}{2} = \pm \sqrt{\frac{1 + \cos \theta}{2}}\) \(\tan \frac{\theta}{2} = \pm \sqrt{\frac{1 - \cos \theta}{1 + \cos \theta}}\)
Sum and Difference Identities
These identities express the sine, cosine, and tangent of the sum or difference of two angles:
\(\sin(\alpha \pm \beta) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta\) \(\cos(\alpha \pm \beta) = \cos \alpha \cos \beta \mp \sin \alpha \sin \beta\) \(\tan(\alpha \pm \beta) = \frac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta}\)
Product-to-Sum and Sum-to-Product Identities
These identities convert products of sines and cosines into sums or differences:
\(\sin A \sin B = \frac{1}{2} [\cos(A - B) - \cos(A + B)]\) \(\cos A \cos B = \frac{1}{2} [\cos(A - B) + \cos(A + B)]\) \(\sin A \cos B = \frac{1}{2} [\sin(A + B) + \sin(A - B)]\)
Applications of Trigonometric Identities
Trigonometric identities involving squares are not just theoretical; they have practical applications in various fields such as physics, engineering, and computer science. For example, they are used in signal processing, analyzing periodic functions, and solving differential equations.
Advanced Problem Solving
Advanced problem-solving in algebra often involves dealing with more complex equations and using various methods to find solutions. Below are some techniques and examples to illustrate these methods.
Quadratic Equations
Quadratic equations are in the form \( ax^2 + bx + c = 0 \). To solve these, we can use several methods:
- Factoring: Find two numbers that multiply to \( ac \) and add to \( b \).
- Example: Solve \( x^2 - 3x - 4 = 0 \).
- Find factors of \(-4\) that add to \(-3\): \((x - 4)(x + 1) = 0\).
- Set each factor to zero: \( x - 4 = 0 \) or \( x + 1 = 0 \).
- Solutions: \( x = 4 \) or \( x = -1 \).
- Example: Solve \( x^2 - 3x - 4 = 0 \).
- Completing the Square: Rewrite the equation in the form \((x + d)^2 = e\).
- Example: Solve \( x^2 + 6x + 9 = 0 \).
- Move constant term: \( x^2 + 6x = -9 \).
- Add and subtract \((\frac{6}{2})^2\): \( x^2 + 6x + 9 = 0 \).
- Rewrite as a square: \( (x + 3)^2 = 0 \).
- Solution: \( x = -3 \).
- Example: Solve \( x^2 + 6x + 9 = 0 \).
- Quadratic Formula: Use \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \).
- Example: Solve \( 2x^2 - 4x - 6 = 0 \).
- Identify coefficients: \( a = 2, b = -4, c = -6 \).
- Plug into formula: \( x = \frac{4 \pm \sqrt{16 + 48}}{4} \).
- Simplify: \( x = \frac{4 \pm \sqrt{64}}{4} = \frac{4 \pm 8}{4} \).
- Solutions: \( x = 3 \) or \( x = -1 \).
- Example: Solve \( 2x^2 - 4x - 6 = 0 \).
Systems of Equations
Solving systems of equations can be done using substitution, elimination, or matrix methods:
- Substitution: Solve one equation for a variable and substitute into the other.
- Example: Solve \( y = 2x + 3 \) and \( x + y = 5 \).
- Substitute \( y \) into the second equation: \( x + 2x + 3 = 5 \).
- Simplify: \( 3x + 3 = 5 \).
- Solve for \( x \): \( x = \frac{2}{3} \).
- Substitute \( x \) back: \( y = 2(\frac{2}{3}) + 3 = \frac{10}{3} \).
- Example: Solve \( y = 2x + 3 \) and \( x + y = 5 \).
- Elimination: Add or subtract equations to eliminate a variable.
- Example: Solve \( 2x + 3y = 6 \) and \( 4x - 3y = 12 \).
- Add equations to eliminate \( y \): \( 6x = 18 \).
- Solve for \( x \): \( x = 3 \).
- Substitute \( x \) back: \( 2(3) + 3y = 6 \), solve \( y = 0 \).
- Example: Solve \( 2x + 3y = 6 \) and \( 4x - 3y = 12 \).
- Matrix Method: Use matrices and row reduction to solve.
- Example: Solve using augmented matrix \( \left[\begin{array}{cc|c}
2 & 3 & 6 \\
4 & -3 & 12 \\
\end{array}\right] \).
- Row reduce to echelon form: \( \left[\begin{array}{cc|c} 1 & 0 & 3 \\ 0 & 1 & 0 \\ \end{array}\right] \).
- Solutions: \( x = 3 \), \( y = 0 \).
- Example: Solve using augmented matrix \( \left[\begin{array}{cc|c}
2 & 3 & 6 \\
4 & -3 & 12 \\
\end{array}\right] \).
Complex Numbers
Solving equations with complex numbers involves using \( i \) where \( i^2 = -1 \):
- Addition/Subtraction: Combine like terms.
- Example: \( (3 + 2i) + (1 - 4i) = 4 - 2i \).
- Multiplication: Use distributive property.
- Example: \( (2 + 3i)(1 + 4i) = 2 + 8i + 3i + 12(-1) = -10 + 11i \).
- Division: Multiply by the conjugate.
- Example: \( \frac{1 + 2i}{3 - 4i} \cdot \frac{3 + 4i}{3 + 4i} = \frac{3 + 4i + 6i + 8}{9 + 16} = \frac{11 + 10i}{25} = \frac{11}{25} + \frac{10i}{25} \).
By mastering these advanced techniques, you can tackle a wide range of algebraic problems with confidence.
Common Mistakes and How to Avoid Them
Understanding and solving quadratic equations often involve common mistakes that can be avoided with proper techniques. Here are some of the frequent errors and tips on how to avoid them:
- Ignoring the Negative Root
- Incorrect Distribution
- Misapplying the Square Root
- Forgetting to Apply Both Positive and Negative Values
- Incorrectly Simplifying Fractions
- Exponents Misinterpretation
- Misusing the Equals Sign
- Order of Operations Errors
- Incorrect Factoring
- Inaccurate Handling of Variables
When solving equations like \( x^2 = 9 \), remember that both \( x = 3 \) and \( x = -3 \) are solutions. Always consider both positive and negative roots when taking the square root of both sides.
Students often mistakenly distribute powers or fail to properly apply the distributive property. For example, \( (a + b)^2 \neq a^2 + b^2 \). The correct expansion is \( (a + b)^2 = a^2 + 2ab + b^2 \).
Remember that \( \sqrt{a^2 + b^2} \neq a + b \). The square root of a sum of squares cannot be simplified into a sum of the square roots. For example, \( \sqrt{x^2 + y^2} \) remains as is.
When dealing with \( x^2 \) equations, always consider both \( x \) and \( -x \) as solutions. This applies to solving equations like \( x^2 = 25 \), where \( x = 5 \) or \( x = -5 \).
A common mistake is simplifying fractions incorrectly, for example, \( \frac{x}{x + y} \neq \frac{x}{x} + \frac{x}{y} \). Instead, the fraction should be simplified within its terms properly.
When working with exponents, remember the correct rules: \( (x^a)^b = x^{a \cdot b} \) and \( x^a \cdot x^b = x^{a+b} \). A common mistake is mixing these rules or applying them incorrectly.
The equals sign should maintain balance on both sides of an equation. Mistakes happen when students perform different operations on each side, disrupting the equality.
Always follow the proper order of operations (PEMDAS/BODMAS): Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right). For example, \( -5^2 \) should be computed as \( -(5^2) = -25 \) not \( (-5)^2 = 25 \).
Ensure proper factoring techniques are applied. For example, factoring \( x^2 - 5x = 2 \) should result in \( x^2 - 5x - 2 = 0 \) and then solve using appropriate methods, rather than making invalid factorizations.
When manipulating variables, ensure accuracy in operations. For instance, \( x(a/b) \) should be handled with care to avoid wrong interpretations such as \( (xa)/b \neq x(a/b) \).
By recognizing and addressing these common mistakes, students can improve their problem-solving skills and accuracy in algebraic manipulations.
Practical Applications in Various Fields
Quadratic equations and functions, particularly those involving \( x^2 \), have numerous practical applications across different fields. Understanding these applications can help illustrate the importance of mastering quadratic concepts. Here are some key areas where \( x^2 \) plays a crucial role:
- Physics:
Quadratic equations are used in various physics problems, such as calculating the motion of objects under the influence of gravity. The equation of motion under constant acceleration, \( s = ut + \frac{1}{2}at^2 \), where \( s \) is the displacement, \( u \) is the initial velocity, \( a \) is the acceleration, and \( t \) is the time, involves the square of time \( t^2 \).
- Engineering:
In engineering, quadratic equations are used in the analysis of structures and materials. For example, the stress-strain relationship in materials can often be modeled using quadratic functions to predict the behavior under various loads.
- Economics:
Quadratic functions are used in economics to model cost functions, revenue functions, and profit maximization problems. For instance, a company's total cost function might be expressed as \( C(x) = ax^2 + bx + c \), where \( x \) is the quantity of goods produced.
- Biology:
In biology, quadratic models are used to describe population growth under certain conditions. The logistic growth model, which includes a quadratic term, helps in understanding how populations grow in an environment with limited resources.
- Architecture:
Architects use quadratic equations to design various elements of buildings, such as parabolic arches and domes. The parabolic shapes are derived from quadratic functions, ensuring stability and aesthetic appeal.
- Astronomy:
In astronomy, the orbits of planets and other celestial bodies can be described using conic sections, which include parabolas, ellipses, and hyperbolas. The equations of these curves are quadratic in nature.
- Finance:
Quadratic functions are employed in financial modeling to predict investment returns and to analyze risk. For example, the calculation of compound interest involves the square of time, showing how investments grow over time.
These examples highlight the versatility and importance of quadratic equations in solving real-world problems. By understanding and applying the principles of \( x^2 \), one can approach complex scenarios with greater confidence and precision.
Additional Resources for Learning
Learning about quadratic equations and their applications can be greatly enhanced by utilizing a variety of resources. Below are some recommended resources that can help you deepen your understanding and practice problem-solving skills.
-
Interactive Tutorials:
- - An interactive tool that helps you solve quadratic equations by entering the coefficients and observing the solution process.
- - Comprehensive video tutorials and practice problems on solving quadratic equations, factoring, and using the quadratic formula.
-
Practice Problems:
- - Provides step-by-step solutions to quadratic equations and offers additional practice problems to test your skills.
- - A textbook-style resource with detailed explanations and examples of solving quadratic equations, along with practice exercises.
-
Supplementary Reading:
- - A free online textbook that covers quadratic equations and functions, offering both reading material and interactive exercises.
- - A free, peer-reviewed textbook that provides a comprehensive overview of algebraic principles, including quadratic equations and their applications.
-
Graphing Tools:
- - An online graphing calculator that allows you to visualize quadratic functions and their solutions.
- - A dynamic mathematics software that helps you graph quadratic equations and explore their properties.
These resources are designed to support your learning journey, providing a mix of instructional material, practice problems, and interactive tools to help you master the topic of quadratic equations.
Giải phương trình x bình phương = 4 và các giá trị khác của x


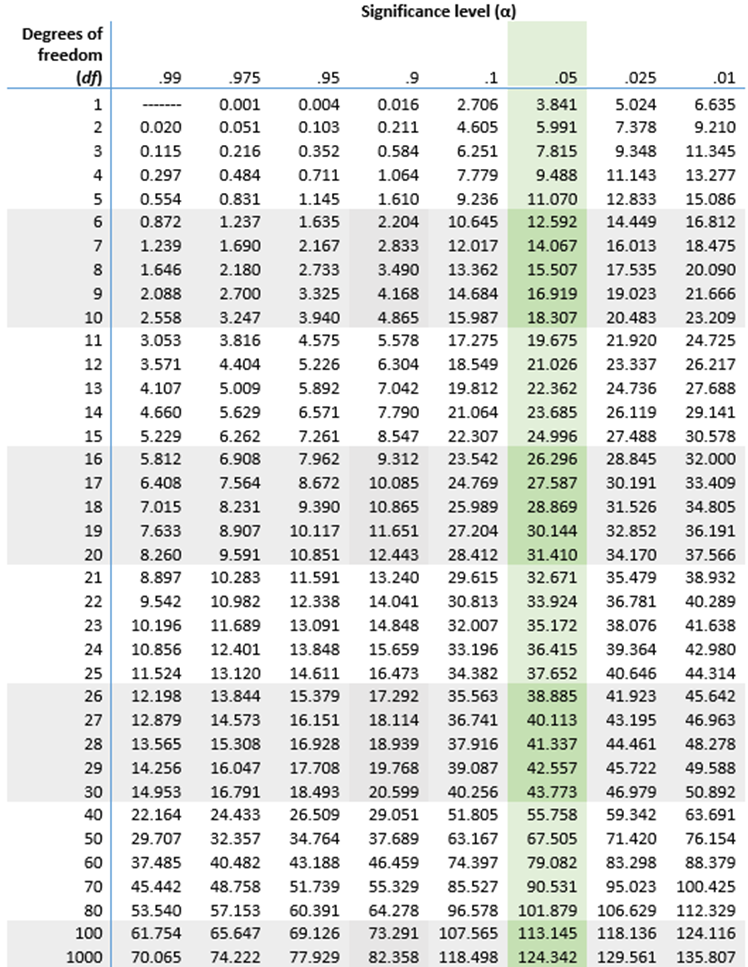
:max_bytes(150000):strip_icc()/Chi-SquareStatistic_Final_4199464-7eebcd71a4bf4d9ca1a88d278845e674.jpg)