Topic what is the perimeter of a parallelogram: Understanding the perimeter of a parallelogram is essential for geometry enthusiasts and students alike. In this guide, we will explore the definition, properties, and various methods to calculate the perimeter, providing you with a clear and concise understanding of this fundamental geometric concept. Dive in to enhance your mathematical skills!
Table of Content
- Perimeter of a Parallelogram
- Introduction to Parallelograms
- Definition and Properties of Parallelograms
- Basic Formula for the Perimeter
- Perimeter Using Side Lengths
- Perimeter Using Diagonals and One Side
- Perimeter Using Base, Height, and Angle
- Examples and Practice Problems
- Application in Real-World Problems
- FAQs on Parallelogram Perimeter
- Common Mistakes and How to Avoid Them
- Advanced Topics in Parallelogram Geometry
- Summary and Key Takeaways
- YOUTUBE: Hướng dẫn chi tiết về cách tính chu vi của hình bình hành. Video này cung cấp các phương pháp và ví dụ minh họa giúp bạn nắm vững cách tính chu vi hình học này.
Perimeter of a Parallelogram
The perimeter of a parallelogram is the total distance around the outside of the parallelogram. It can be calculated using different formulas depending on the known parameters of the parallelogram. Below are various methods and examples for calculating the perimeter.
Using Side Lengths
If the lengths of the adjacent sides \( a \) and \( b \) of a parallelogram are known, the perimeter \( P \) is given by:
\[
P = 2(a + b)
\]
For example, if \( a = 5 \, \text{cm} \) and \( b = 7 \, \text{cm} \), then:
\[
P = 2(5 + 7) = 2 \times 12 = 24 \, \text{cm}
\]
Using One Side and Diagonals
If one side \( a \) and the lengths of the diagonals \( d_1 \) and \( d_2 \) are known, the perimeter \( P \) can be calculated using the formula:
\[
P = 2a + 2\sqrt{ \left( \frac{d_1^2 + d_2^2}{2} - a^2 \right)}
\]
For example, if \( a = 8 \, \text{cm} \), \( d_1 = 10 \, \text{cm} \), and \( d_2 = 12 \, \text{cm} \), then:
\[
P = 2(8) + 2\sqrt{ \left( \frac{10^2 + 12^2}{2} - 8^2 \right)} = 16 + 2\sqrt{ \left( \frac{100 + 144}{2} - 64 \right)} = 16 + 2\sqrt{ \left( 122 - 64 \right)} = 16 + 2\sqrt{ 58 } \approx 32.25 \, \text{cm}
\]
Using Base, Height, and Angle
If the base \( a \), height \( h \), and an angle \( \theta \) of the parallelogram are known, the perimeter \( P \) can be found using the formula:
\[
P = 2a + 2\left( \frac{h}{\sin(\theta)} \right)
\]
For example, if \( a = 15 \, \text{yards} \), \( h = 20 \, \text{yards} \), and \( \theta = 30^\circ \), then:
\[
P = 2(15) + 2\left( \frac{20}{\sin(30^\circ)} \right) = 30 + 2 \times 40 = 30 + 80 = 110 \, \text{yards}
\]
Examples and Applications
-
Example 1: Find the perimeter of a parallelogram with side lengths 6 cm and 9 cm.
\[
P = 2(6 + 9) = 2 \times 15 = 30 \, \text{cm}
\] -
Example 2: Calculate the perimeter of a parallelogram where one side is 8 inches, and the diagonals are 10 inches and 12 inches.
\[
P = 2(8) + 2\sqrt{ \left( \frac{10^2 + 12^2}{2} - 8^2 \right)} \approx 31.23 \, \text{inches}
\] -
Example 3: Determine the perimeter of a parallelogram with one side 15 yards, height 20 yards, and an angle of 30 degrees.
\[
P = 2(15) + 2\left( \frac{20}{\sin(30^\circ)} \right) = 110 \, \text{yards}
\]
Summary
The perimeter of a parallelogram can be calculated using various formulas based on the known dimensions. Whether you have the lengths of the sides, the diagonals, or the base and height along with an angle, there is a formula to help you find the perimeter efficiently.
READ MORE:
Introduction to Parallelograms
A parallelogram is a four-sided polygon with opposite sides that are both equal in length and parallel to each other. This unique property leads to several interesting characteristics and formulas used in geometry.
Key properties of a parallelogram include:
- Opposite sides are equal and parallel.
- Opposite angles are equal.
- The diagonals bisect each other.
- The sum of the interior angles is 360 degrees.
The perimeter of a parallelogram is the total distance around the outside of the shape. It can be calculated using various methods depending on the known dimensions.
- Using side lengths: \( P = 2(a + b) \) where \( a \) and \( b \) are the lengths of the adjacent sides.
- Using diagonals and one side: In specific cases, when one side and both diagonals are known, additional formulas involving trigonometric functions might be used.
- Using base, height, and angle: When the base, height, and one angle are known, trigonometric identities can help in finding the perimeter.
Understanding these properties and formulas is crucial for solving geometric problems involving parallelograms. This guide will delve into these aspects in detail, providing examples and practice problems to enhance your comprehension.
Definition and Properties of Parallelograms
A parallelogram is a quadrilateral with two pairs of parallel sides. The defining feature of a parallelogram is that its opposite sides are both equal in length and parallel. This symmetry gives rise to several important geometric properties.
Key properties of parallelograms include:
- Opposite sides are equal and parallel: \( AB \parallel CD \) and \( AD \parallel BC \) with \( AB = CD \) and \( AD = BC \).
- Opposite angles are equal: \( \angle A = \angle C \) and \( \angle B = \angle D \).
- Consecutive angles are supplementary: \( \angle A + \angle B = 180^\circ \).
- The diagonals bisect each other: The point where the diagonals intersect divides each diagonal into two equal parts.
- The sum of the interior angles is always 360 degrees.
The perimeter \( P \) of a parallelogram is calculated as the sum of the lengths of its four sides. Since opposite sides are equal, the formula for the perimeter is:
\[
P = 2(a + b)
\]
where \( a \) and \( b \) are the lengths of adjacent sides.
In addition to these basic properties, parallelograms also exhibit symmetry in their diagonals and can be classified into special types such as rectangles, rhombuses, and squares, each having additional unique properties.
Understanding these properties allows for the effective solving of various geometric problems involving parallelograms, from simple perimeter calculations to more complex applications.
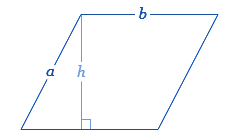
Basic Formula for the Perimeter
The perimeter of a parallelogram is calculated by summing the lengths of all its sides. Since opposite sides of a parallelogram are equal in length, the formula for the perimeter simplifies to:
Where a and b are the lengths of the adjacent sides of the parallelogram.
Step-by-Step Example
Let's calculate the perimeter of a parallelogram with side lengths of 5 units and 9 units:
- Identify the lengths of the adjacent sides:
- a = 5 units
- b = 9 units
- Substitute the values into the formula:
- Simplify the expression:
- Multiply:
Important Notes
- The perimeter of a parallelogram is always twice the sum of its adjacent sides.
- In cases where the diagonals and one side are known, the perimeter can be calculated using a more complex formula involving the diagonals.
Perimeter Using Side Lengths
The perimeter of a parallelogram can be calculated using the lengths of its sides. Since the opposite sides of a parallelogram are equal, the formula for the perimeter is straightforward.
The basic formula for the perimeter \( P \) of a parallelogram, given the lengths of two adjacent sides \( a \) and \( b \), is:
Here's a step-by-step explanation:
Identify the lengths of the two adjacent sides of the parallelogram. Let's denote these lengths as \( a \) and \( b \).
Sum the lengths of these two sides:
(a + b) .Multiply the sum by 2 to account for both pairs of opposite sides:
P = 2(a + b) .
For example, if a parallelogram has sides of length 8 cm and 5 cm, the perimeter calculation would be:
This formula is useful because it leverages the property that opposite sides of a parallelogram are equal in length.
Examples
Example 1: Find the perimeter of a parallelogram with side lengths 6 units and 9 units.
P = 2(6 + 9) = 2(15) = 30 \text{ units} Example 2: Find the perimeter of a parallelogram with side lengths 7 cm and 4 cm.
P = 2(7 + 4) = 2(11) = 22 \text{ cm}
This simple method allows for quick and accurate calculation of the perimeter using just the side lengths of the parallelogram.

Perimeter Using Diagonals and One Side
The perimeter of a parallelogram can be determined using its diagonals and one of its sides. This method requires understanding the relationship between the diagonals, the side lengths, and the angles within the parallelogram.
To find the perimeter using diagonals and one side, follow these steps:
- Identify the given values: Let \(d_1\) and \(d_2\) be the lengths of the diagonals, and let \(a\) be the length of one side.
- Use the relationship between diagonals and sides: In a parallelogram, the diagonals bisect each other. Let \( \theta \) be the angle between the diagonals at the intersection point. The relationship is given by:
\[d_1^2 + d_2^2 = 2a^2 + 2b^2 - 4ab\cos(\theta)\] where \(b\) is the length of the other side. However, for simplicity, we approximate \(b\) using: \[b = \sqrt{a^2 + d_1^2 + d_2^2 - 2ad_1 - 2ad_2}\] - Calculate the other side length: Use the approximation:
\[ b \approx \sqrt{a^2 + \left(\frac{d_1}{2}\right)^2 + \left(\frac{d_2}{2}\right)^2} \] - Determine the perimeter: Once both side lengths \(a\) and \(b\) are known, calculate the perimeter \(P\):
\[ P = 2a + 2b \]
Example:
Suppose we have a parallelogram with diagonals of lengths \(d_1 = 10\) units and \(d_2 = 8\) units, and one side length \(a = 6\) units. Using the above method:
- Identify given values: \(d_1 = 10\), \(d_2 = 8\), and \(a = 6\).
- Approximate the other side \(b\):
\[ b \approx \sqrt{6^2 + \left(\frac{10}{2}\right)^2 + \left(\frac{8}{2}\right)^2} = \sqrt{6^2 + 5^2 + 4^2} = \sqrt{36 + 25 + 16} = \sqrt{77} \approx 8.77 \] - Calculate the perimeter:
\[ P = 2 \times 6 + 2 \times 8.77 = 12 + 17.54 = 29.54 \text{ units} \]
This method provides an approximate way to determine the perimeter when the diagonals and one side are known.
Perimeter Using Base, Height, and Angle
To find the perimeter of a parallelogram using the base, height, and an angle, follow these steps:
- Identify the given values: Let \( b \) be the base, \( h \) be the height, and \( \theta \) be the angle between the base and the side.
- Calculate the side length: Use the height and angle to find the length of the side opposite the angle \( \theta \). This is calculated by:
\[ a = \frac{h}{\sin(\theta)} \] where \( a \) is the length of the side. - Calculate the adjacent side: Use the base and angle to find the length of the adjacent side. This is calculated by:
\[ l = b - h \cot(\theta) \] where \( l \) is the length of the adjacent side. - Determine the perimeter: Once the side lengths \( a \) and \( l \) are known, the perimeter \( P \) is:
\[ P = 2a + 2l \]
Example:
Consider a parallelogram with base \( b = 10 \) units, height \( h = 6 \) units, and angle \( \theta = 30^\circ \). Using the method:
- Identify given values: \( b = 10 \), \( h = 6 \), \( \theta = 30^\circ \).
- Calculate the side length \( a \):
\[ a = \frac{6}{\sin(30^\circ)} = \frac{6}{0.5} = 12 \text{ units} \] - Calculate the adjacent side \( l \):
\[ l = 10 - 6 \cot(30^\circ) = 10 - 6 \cdot \frac{\sqrt{3}}{3} \approx 10 - 6 \cdot 0.577 = 10 - 3.462 = 6.538 \text{ units} \] - Calculate the perimeter:
\[ P = 2 \times 12 + 2 \times 6.538 = 24 + 13.076 = 37.076 \text{ units} \]
In this way, the perimeter of the parallelogram can be calculated using the base, height, and an angle.
Examples and Practice Problems
Let's solve some examples and practice problems to solidify our understanding of finding the perimeter of a parallelogram.
- Example 1: Given a parallelogram with side lengths of 6 cm and 8 cm, find its perimeter.
- Example 2: If the diagonals of a parallelogram are 10 cm and 12 cm, and one side is 6 cm, what is its perimeter?
We know that the perimeter of a parallelogram is the sum of all its side lengths. In this case, the parallelogram has opposite sides of equal length, so the perimeter is:
Perimeter = 6 cm + 8 cm + 6 cm + 8 cm
Perimeter = 28 cm
To find the perimeter, we add up all the side lengths. Since the diagonals bisect each other in a parallelogram, we can use the Pythagorean theorem to find the other half of the side lengths. Let's denote half of the longer diagonal as 'a' and half of the shorter diagonal as 'b'. So,
\(a^2 = 12^2 - 6^2 = 144 - 36 = 108 \Rightarrow a = \sqrt{108} = 6\sqrt{3}\) cm
\(b^2 = 10^2 - 6^2 = 100 - 36 = 64 \Rightarrow b = \sqrt{64} = 8\) cm
Now, we find the perimeter:
Perimeter = 6 cm + 6 cm + 8 cm + 8 cm
Perimeter = 28 cm
Application in Real-World Problems
Let's explore how understanding the perimeter of a parallelogram can be applied to solve real-world problems:
- Example 1: Fencing a Rectangular Field
- Example 2: Finding the Boundary of a Lake
Imagine you have a rectangular field with a length of 50 meters and a width of 30 meters. To fence the field, you need to find the perimeter.
Perimeter = 2(length + width)
Perimeter = 2(50 m + 30 m)
Perimeter = 2(80 m)
Perimeter = 160 meters
So, to fence the rectangular field, you would need 160 meters of fencing material.
Suppose there's a lake in the shape of a parallelogram. To determine the distance around the lake, we need to calculate its perimeter.
Perimeter = 2(side1 + side2)
After measuring the sides of the lake, let's say side1 is 120 meters and side2 is 90 meters.
Perimeter = 2(120 m + 90 m)
Perimeter = 2(210 m)
Perimeter = 420 meters
Therefore, the boundary of the lake measures 420 meters.
FAQs on Parallelogram Perimeter
Here are some frequently asked questions about finding the perimeter of a parallelogram:
- What is the formula to calculate the perimeter of a parallelogram?
- Do all sides of a parallelogram have the same length?
- Can we use the Pythagorean theorem to find the perimeter of a parallelogram?
- How can we find the perimeter if the lengths of all sides are not given?
- Is the perimeter of a parallelogram affected by the angle between its adjacent sides?
The formula to find the perimeter of a parallelogram is:
Perimeter = 2 × (Length + Width)
No, all sides of a parallelogram do not necessarily have the same length. However, opposite sides of a parallelogram are equal in length.
No, the Pythagorean theorem is used to find the lengths of sides in right-angled triangles. It cannot be directly applied to find the perimeter of a parallelogram.
If the lengths of all sides are not given, we can find the perimeter by using the lengths of the given sides or by using other properties such as diagonals and angles.
No, the perimeter of a parallelogram is not affected by the angle between its adjacent sides. It is solely determined by the lengths of its sides.
Common Mistakes and How to Avoid Them
Let's address some common mistakes made when calculating the perimeter of a parallelogram and how to avoid them:
- Mistake: Adding only two sides instead of all four sides when finding the perimeter.
- Mistake: Incorrectly calculating the length of the sides or diagonals.
- Mistake: Using the wrong formula to find the perimeter.
- Mistake: Neglecting to consider units of measurement.
- Mistake: Forgetting to account for angles in special cases.
To avoid this mistake, remember that the perimeter of a parallelogram is the sum of all its side lengths, not just two opposite sides.
Ensure accurate measurements and use appropriate formulas to calculate side lengths or diagonals if necessary. Double-check your calculations to avoid errors.
Always use the correct formula for finding the perimeter of a parallelogram, which is 2 × (Length + Width).
When performing calculations, ensure all measurements are in the same units to avoid errors in the final result.
In some cases, angles may affect the calculation of the perimeter, especially if the parallelogram is not a rectangle. Pay attention to angle measurements if provided.
Advanced Topics in Parallelogram Geometry
In this section, we delve into more complex and intriguing aspects of parallelogram geometry, exploring various advanced topics that enhance our understanding of this fundamental shape.
1. Perimeter Using Coordinates
When given the coordinates of the vertices of a parallelogram, we can calculate the perimeter using the distance formula. If the vertices are \(A(x_1, y_1)\), \(B(x_2, y_2)\), \(C(x_3, y_3)\), and \(D(x_4, y_4)\), the perimeter \(P\) can be found as follows:
- Calculate the distance between adjacent vertices:
- AB: \(\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\)
- BC: \(\sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2}\)
- CD: \(\sqrt{(x_4 - x_3)^2 + (y_4 - y_3)^2}\)
- DA: \(\sqrt{(x_1 - x_4)^2 + (y_1 - y_4)^2}\)
- Sum the lengths of all sides to get the perimeter:
\(P = AB + BC + CD + DA\)
2. Perimeter in Vector Form
Using vectors, the perimeter can be determined by considering the vectors representing the sides of the parallelogram. If vectors \(\vec{u}\) and \(\vec{v}\) represent adjacent sides, the perimeter \(P\) is given by:
\(P = 2 \left( \|\vec{u}\| + \|\vec{v}\| \right)\)
Here, \(\|\vec{u}\|\) and \(\|\vec{v}\|\) are the magnitudes of the vectors.
3. Perimeter in Terms of Diagonals
For a parallelogram, the relationship between the sides and diagonals can also help in calculating the perimeter. If \(d_1\) and \(d_2\) are the lengths of the diagonals, and \(\theta\) is the angle between them, the perimeter can be expressed as:
\(P = 2 \left( \sqrt{\frac{d_1^2 + d_2^2 + 2d_1 d_2 \cos(\theta)}{2}} + \sqrt{\frac{d_1^2 + d_2^2 - 2d_1 d_2 \cos(\theta)}{2}} \right)\)
4. Perimeter in Relation to Area
The perimeter can also be related to the area \(A\) and the height \(h\) of the parallelogram. If \(b\) is the base length, we have:
\(P = 2(b + \frac{A}{h})\)
5. Perimeter with Transformations
Understanding how transformations affect the perimeter of a parallelogram is crucial in advanced geometry. Common transformations include:
- Translation: Does not change the perimeter.
- Rotation: Does not change the perimeter.
- Scaling: If a parallelogram is scaled by a factor \(k\), the new perimeter \(P'\) is given by \(P' = kP\).
6. Perimeter and Symmetry
Analyzing the symmetry properties of parallelograms can lead to deeper insights into their geometry. Parallelograms exhibit rotational symmetry of order 2 and reflection symmetry across both diagonals.
These advanced topics provide a comprehensive understanding of the perimeter of parallelograms, highlighting the versatility and depth of this geometric shape.
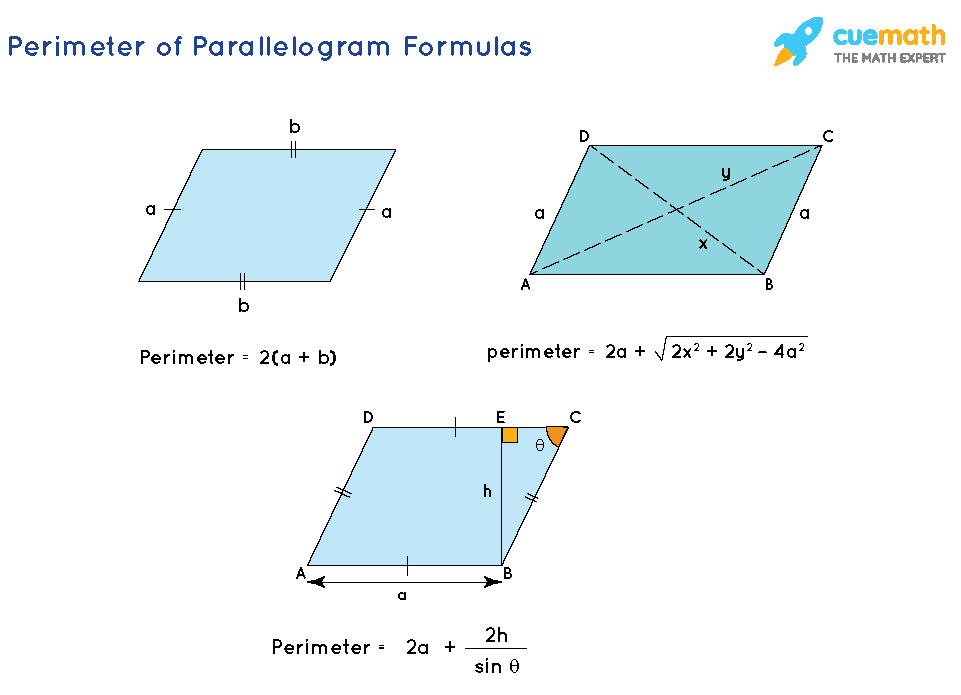
Summary and Key Takeaways
Understanding the perimeter of a parallelogram is essential for both theoretical and practical applications in geometry. Here are the key points to remember:
- The perimeter of a parallelogram is the total distance around its boundary, calculated as the sum of the lengths of all four sides.
- Given the nature of parallelograms, where opposite sides are equal in length, the perimeter can be succinctly expressed with the formula:
- Here, a and b are the lengths of any two adjacent sides.
- In situations where one side and the lengths of the diagonals are known, the perimeter can be found using the formula:
- In this formula, a is the known side length, and x and y are the lengths of the diagonals.
- Alternatively, when the base length, height, and an angle are known, the perimeter can be calculated using trigonometric relationships:
- Here, a is the base, h is the height, and \( \theta \) is the angle between the base and the side of the parallelogram.
\( P = 2(a + b) \)
\( P = 2a + \sqrt{2x^2 + 2y^2 - 4a^2} \)
\( P = 2a + \frac{2h}{\sin(\theta)} \)
These formulas allow for flexibility depending on the given parameters and can be applied in various problem-solving scenarios:
- Simple Perimeter Calculation: Using the basic formula \( P = 2(a + b) \), calculate the perimeter when side lengths are known.
- Complex Scenarios: Utilize the formula involving diagonals or trigonometric methods for cases with additional geometric information.
In summary, the perimeter of a parallelogram is versatile in its calculation methods, providing multiple pathways depending on the given information. This understanding is crucial for solving both academic problems and practical tasks in fields such as engineering and architecture.
Hướng dẫn chi tiết về cách tính chu vi của hình bình hành. Video này cung cấp các phương pháp và ví dụ minh họa giúp bạn nắm vững cách tính chu vi hình học này.
Làm Thế Nào Để Tìm Chu Vi Hình Bình Hành
READ MORE:
Video này hướng dẫn chi tiết về cách tính diện tích và chu vi của hình bình hành. Khám phá các công thức và ví dụ minh họa để hiểu rõ hơn về các phương pháp tính toán hình học này.
Cách Tính Diện Tích và Chu Vi Hình Bình Hành