Topic what is 18 square root: Discover the fascinating world of square roots with a focus on the square root of 18. This comprehensive guide will help you understand what the square root of 18 is, how to calculate it, and its practical applications in real life. Dive in to enhance your mathematical knowledge and skills.
Table of Content
- Square Root of 18
- Introduction to Square Roots
- Definition of Square Root
- Basic Properties of Square Roots
- Calculating the Square Root of 18
- Simplifying the Square Root of 18
- Square Root of 18 in Decimal Form
- Steps to Calculate Manually
- Square Root of 18 Using a Calculator
- Square Root of 18 in Radical Form
- Understanding Irrational Numbers
- Approximation Techniques
- Applications of Square Roots in Real Life
- Practical Examples Involving √18
- Common Mistakes and Misconceptions
- FAQs about Square Root of 18
- Conclusion
- YOUTUBE: Tìm hiểu về căn bậc hai của 18 và cách tính toán, ứng dụng thực tế trong cuộc sống hàng ngày.
Square Root of 18
The square root of 18 is a number that, when multiplied by itself, equals 18. This value is represented mathematically as:
Exact Value
The square root of 18 can be simplified by recognizing that 18 is a product of a perfect square and another number:
\(\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}\)
Decimal Approximation
While the exact value is \(3\sqrt{2}\), it can also be approximated in decimal form:
\(\sqrt{18} \approx 4.242640687\)
Calculation Steps
- Identify that 18 can be broken down into \(9 \times 2\).
- Take the square root of 9, which is 3.
- Multiply the result by the square root of 2, giving \(3\sqrt{2}\).
Properties
- \(\sqrt{18}\) is an irrational number, meaning it cannot be expressed as a simple fraction.
- It is approximately equal to 4.242640687.
- It can be simplified to \(3\sqrt{2}\).
| Exact Form | Decimal Approximation |
| \(3\sqrt{2}\) | 4.242640687 |
Understanding the square root of 18 can help in various mathematical applications, including solving equations and understanding geometric properties.

READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics, used to determine a value that, when multiplied by itself, gives the original number. For example, the square root of 18 is written as \( \sqrt{18} \). This value is essential in various fields, including algebra, geometry, and real-life applications.
Here are some key points to understand about square roots:
- Definition: The square root of a number \( x \) is a value \( y \) such that \( y^2 = x \).
- Notation: The square root of a number is denoted by the radical symbol \( \sqrt{} \). For example, \( \sqrt{18} \).
- Properties:
- The square root of a positive number is always positive.
- Every positive number has two square roots: one positive and one negative. However, the principal square root is the positive one.
- The square root of zero is zero.
- Negative numbers do not have real square roots, as the product of two positive or two negative numbers is always positive.
- Examples:
- \( \sqrt{4} = 2 \) because \( 2^2 = 4 \).
- \( \sqrt{9} = 3 \) because \( 3^2 = 9 \).
- \( \sqrt{18} \approx 4.24 \) because \( 4.24^2 \approx 18 \).
Square roots play a crucial role in solving equations, analyzing geometric shapes, and even in real-life scenarios such as physics and engineering. Understanding square roots opens up a wide range of mathematical possibilities and applications.
Definition of Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical symbol "√". For instance, the square root of 18 is represented as √18.
Mathematically, the principal square root of 18 is written as:
\[ \sqrt{18} \]
Square roots can be expressed in various forms:
- Radical Form: √18
- Exponent Form: \( 18^{1/2} \)
The square root of 18 can also be simplified by expressing it in terms of its prime factors. The prime factorization of 18 is:
\[ 18 = 2 \times 3^2 \]
Therefore, the square root of 18 can be simplified as:
\[ \sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2} \]
This indicates that the square root of 18 in its simplest radical form is \( 3\sqrt{2} \).
In decimal form, the square root of 18 is approximately:
\[ \sqrt{18} \approx 4.24264068712 \]
It is important to note that the square root of 18 is an irrational number, meaning it cannot be exactly expressed as a fraction of two integers, and its decimal representation is non-terminating and non-repeating.
Every positive number has two square roots: one positive and one negative. Therefore, the square roots of 18 are:
\[ \sqrt{18} = ±3\sqrt{2} \]
This can be represented as:
- Positive square root: \( 3\sqrt{2} \)
- Negative square root: \( -3\sqrt{2} \)
Basic Properties of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. The basic properties of square roots are essential in understanding their behavior in mathematics.
- Non-Negative Result: The square root of a non-negative number is always non-negative. For example, \( \sqrt{25} = 5 \) and \( \sqrt{0} = 0 \).
- Product Property: The square root of a product is the product of the square roots of the factors. Mathematically, \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \). For example, \( \sqrt{16 \cdot 25} = \sqrt{16} \cdot \sqrt{25} = 4 \cdot 5 = 20 \).
- Quotient Property: The square root of a quotient is the quotient of the square roots of the numerator and the denominator. Mathematically, \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). For example, \( \sqrt{\frac{49}{9}} = \frac{\sqrt{49}}{\sqrt{9}} = \frac{7}{3} \).
- Square of a Square Root: The square of a square root returns the original number, \( (\sqrt{a})^2 = a \). For example, \( (\sqrt{9})^2 = 9 \).
- Addition and Subtraction: Square roots cannot be directly added or subtracted in the same way as integers. For instance, \( \sqrt{a} + \sqrt{b} \neq \sqrt{a + b} \).
- Rational and Irrational Numbers: The square root of a perfect square is a rational number, while the square root of a non-perfect square is an irrational number. For example, \( \sqrt{25} = 5 \) (rational), but \( \sqrt{2} \) is irrational.
Understanding these properties is crucial for simplifying expressions involving square roots and for solving equations where square roots appear.
| Property | Example |
|---|---|
| Non-Negative Result | \( \sqrt{36} = 6 \) |
| Product Property | \( \sqrt{9 \cdot 4} = \sqrt{9} \cdot \sqrt{4} = 3 \cdot 2 = 6 \) |
| Quotient Property | \( \sqrt{\frac{25}{16}} = \frac{\sqrt{25}}{\sqrt{16}} = \frac{5}{4} \) |
| Square of a Square Root | \( (\sqrt{49})^2 = 49 \) |
| Rational and Irrational Numbers | \( \sqrt{9} = 3 \) (rational), \( \sqrt{3} \) (irrational) |
By mastering these properties, one can solve complex mathematical problems involving square roots more efficiently and accurately.
Calculating the Square Root of 18
The square root of 18 can be calculated using several methods. Here, we will discuss two main methods: the Prime Factorization Method and the Long Division Method.
Prime Factorization Method
- First, find the prime factors of 18:
\(18 = 2 \times 3 \times 3\)
- Group the prime factors into pairs:
\(18 = 2 \times (3 \times 3)\)
- Express the paired factors as squares:
\(18 = 2 \times 3^2\)
- Take the square root of both sides:
\(\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}\)
Thus, the simplified form of the square root of 18 is \(3\sqrt{2}\).
Long Division Method
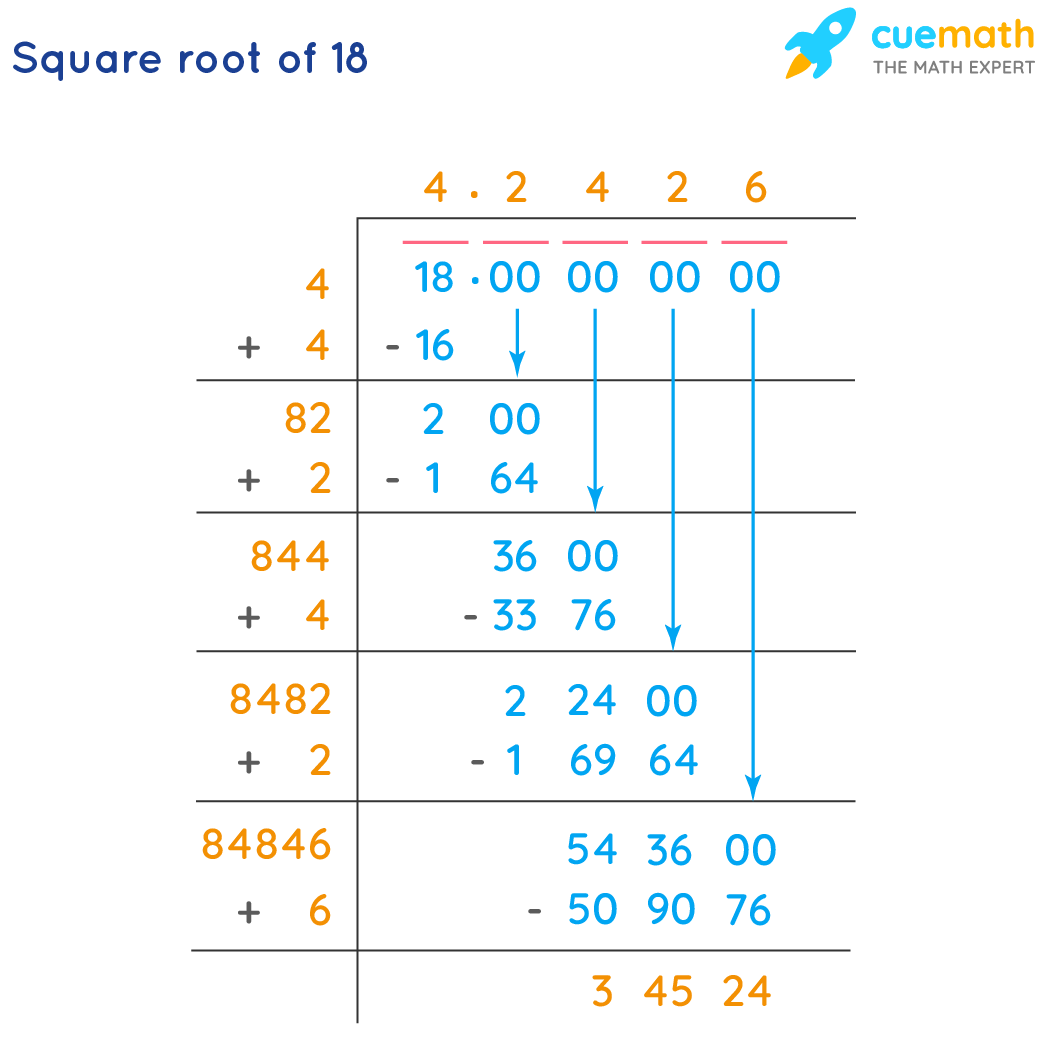
- Start by writing the number 18 as 18.000000 for easier calculation.
- Pair the digits starting from the decimal point: 18 | 00 00 00.
- Find a number that, when squared, is less than or equal to 18. The number 4 works since \(4 \times 4 = 16\).
- Subtract 16 from 18, getting a remainder of 2. Bring down the next pair of zeros to make it 200.
- Double the quotient (4) to get 8. Determine a digit X such that \(8X \times X \leq 200\). The number 2 works because \(82 \times 2 = 164\).
- Continue this process to refine the value to the desired number of decimal places.
Following these steps, the square root of 18 can be approximated as 4.2426.
In summary, the square root of 18 is:
- In radical form: \(3\sqrt{2}\)
- In decimal form: 4.2426 (approximately)

Simplifying the Square Root of 18
Simplifying a square root involves expressing the number inside the square root in its simplest form. For the square root of 18, we need to find the factors of 18, focusing on perfect squares.
Here's the step-by-step process:
- Identify the factors of 18. The factors are 1, 2, 3, 6, 9, and 18.
- Find the largest perfect square factor. In this case, it is 9 (since \(9 = 3^2\)).
- Rewrite the square root of 18 as a product of square roots: \[ \sqrt{18} = \sqrt{9 \times 2} \]
- Use the property of square roots to separate them: \[ \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} \]
- Simplify the square root of the perfect square: \[ \sqrt{9} = 3 \]
- Combine the simplified square roots: \[ \sqrt{9} \times \sqrt{2} = 3\sqrt{2} \]
Therefore, the simplified form of \(\sqrt{18}\) is \(3\sqrt{2}\).
By following these steps, you can simplify square roots of other non-perfect square numbers in a similar manner.
Square Root of 18 in Decimal Form
The square root of 18 can be represented in decimal form as a non-repeating, non-terminating number. This means that when expressed in decimal form, it continues infinitely without repeating a specific sequence of digits.
The approximate value of the square root of 18 in decimal form is:
\[
\sqrt{18} \approx 4.242640687
\]
To understand this better, let's look at the method to derive this decimal value:
Approximation Method
- Identify two perfect squares between which 18 lies. These are 16 (42) and 25 (52).
- Since 18 is closer to 16 than to 25, we know \(\sqrt{18}\) is slightly more than 4.
- Using interpolation, we can get a closer approximation:
- Calculate \(\frac{18 - 16}{25 - 16} = \frac{2}{9} \approx 0.22\)
- Therefore, \(\sqrt{18} \approx 4.22\). For more precision, advanced methods or tools can provide the value up to more decimal places.
Using a Calculator
Most scientific calculators can directly compute the square root of 18. Entering \(\sqrt{18}\) will yield approximately 4.242640687.
Manual Calculation
To manually compute \(\sqrt{18}\) using the long division method:
- Set up 18 in pairs of digits starting from the decimal point. 18.00 00 00 00 ...
- Find the largest number whose square is less than or equal to 18, which is 4 (since \(4^2 = 16\)).
- Subtract \(16\) from \(18\) to get 2. Bring down a pair of zeros to make it 200.
- Double the quotient obtained (4) and write it as the new divisor's first part (8_).
- Find a digit to complete the divisor and also multiply it to get a number less than or equal to 200. Here, 82 × 2 = 164.
- Continue this process to obtain a more precise value.
Following these steps, we approximate \(\sqrt{18} \approx 4.242640687\), providing a highly precise value suitable for most practical purposes.
Steps to Calculate Manually
Manually calculating the square root of 18 involves using the long division method. Here are the detailed steps:
- Setup: Start by writing the number 18 as 18.000000 to facilitate the calculation up to the required decimal places.
- Group Digits: Pair the digits of the number from right to left. Here, 18 becomes 18.000000.
- Initial Division: Find the largest number whose square is less than or equal to 18. This number is 4 because \(4^2 = 16\). Write 4 in the quotient.
- Subtract: Subtract the square of 4 from 18. \(18 - 16 = 2\).
- Bring Down Pairs: Bring down the next pair of zeros, making the number 200.
- Double the Quotient: Double the current quotient (4), getting 8. Write this as the new divisor's starting digit (8_).
- Find Next Digit: Find a digit x such that \(8x \times x\) is less than or equal to 200. The digit is 2, since \(82 \times 2 = 164\).
- Subtract Again: Subtract \(164\) from \(200\), getting 36. Bring down the next pair of zeros, making the number 3600.
- Repeat: Double the quotient (42), getting 84. Find the next digit x such that \(84x \times x\) is less than or equal to 3600. Continue this process until the desired precision is achieved.
The quotient will gradually build up the square root of 18. Through this method, you can determine that the square root of 18 is approximately 4.2426 when rounded to four decimal places.
Square Root of 18 Using a Calculator
Calculating the square root of 18 using a calculator is a straightforward process. Here are the steps to follow:
- Turn on the calculator: Ensure your calculator is on and in the correct mode for calculating square roots. Most scientific and graphing calculators have a square root button (√).
- Enter the number: Type in 18 using the number pad.
- Press the square root button: This button is often represented by a radical symbol (√). Press this button to calculate the square root.
- View the result: The calculator will display the square root of 18, which is approximately \(\sqrt{18} \approx 4.242640687\).
Using a calculator is the fastest and easiest method to find the square root of a number, especially when the number is not a perfect square.
- Note: Different calculators may have different procedures, but the general steps remain the same. Always refer to your calculator's manual if you encounter any issues.
Calculators like Mathway or Good Calculators provide online tools to calculate the square root, which can be very helpful if you do not have a physical calculator at hand.
Square Root of 18 in Radical Form
To express the square root of 18 in radical form, we simplify it to its most reduced radical form. This involves finding the prime factorization of the number and then simplifying the radicals.
Here is a step-by-step process to simplify the square root of 18:
- First, find the prime factorization of 18:
- 18 = 2 × 32
- Next, express the square root of 18 using these prime factors:
- \(\sqrt{18} = \sqrt{2 \times 3^2}\)
- Then, apply the property of square roots that states \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\):
- \(\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}\)
- Simplify the radical by taking the square root of the perfect square (32):
- \(\sqrt{18} = \sqrt{2} \times 3 = 3\sqrt{2}\)
Therefore, the square root of 18 in its simplest radical form is:
\(\sqrt{18} = 3\sqrt{2}\)
This method of simplification shows that the square root of 18 can be expressed in a more manageable and simplified form, which is useful in various mathematical applications and calculations.
Understanding Irrational Numbers
In mathematics, an irrational number is a real number that cannot be expressed as a simple fraction. This means that irrational numbers cannot be written as the ratio of two integers. Their decimal expansions are non-terminating and non-repeating.
One of the most famous examples of an irrational number is π (pi), which represents the ratio of the circumference of a circle to its diameter. Similarly, the square root of 2 (√2) is another well-known irrational number.
The square root of 18 is also an irrational number. When expressed in decimal form, √18 is approximately 4.242640687, which is a non-terminating and non-repeating decimal. This means that it cannot be precisely represented as a fraction of two integers.
To understand why √18 is irrational, consider its radical form:
\[
\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}
\]
Since √2 is known to be irrational, any multiple of √2 (other than zero) is also irrational. Therefore, 3√2 is irrational, making the square root of 18 irrational.
Here are some key properties of irrational numbers:
- Non-terminating and Non-repeating Decimal Expansion: Irrational numbers have decimal expansions that go on forever without repeating.
- Cannot be expressed as a fraction: Unlike rational numbers, irrational numbers cannot be written as the ratio of two integers.
- Unique Properties: The sum or product of a rational number and an irrational number is always irrational. However, the product of two irrational numbers can be rational (e.g., \(\sqrt{2} \times \sqrt{2} = 2\)).
Understanding irrational numbers is crucial in various fields of mathematics and science. They often appear in geometry, trigonometry, and calculus, playing a vital role in calculations and theoretical concepts.
For instance, when dealing with the square root of 18 in practical scenarios, it is essential to recognize its irrational nature. This recognition helps in accurate computations and avoiding common mistakes associated with approximating irrational numbers.
Approximation Techniques
Approximating the square root of a number, like 18, involves several methods that provide accurate results. Here, we will explore two common techniques: the Long Division Method and Newton's Method.
Long Division Method
- Start by writing 18 as the dividend under the division symbol.
- Group the digits in pairs, starting from the decimal point. For 18, it is 18.00.
- Find a number whose square is less than or equal to 18. The closest number is 4 because \(4^2 = 16\).
- Subtract 16 from 18, giving a remainder of 2. Bring down a pair of zeros to make it 200.
- Double the divisor (4), getting 8. Find a digit (x) so that 8x multiplied by x is less than or equal to 200. Here, x is 2, because \(82 \times 2 = 164\).
- Repeat the process with the new remainder (200 - 164 = 36). Bring down another pair of zeros to make it 3600, and continue.
- Continuing this process, you get the square root of 18 as approximately 4.2426.
Newton's Method
- Start with an initial guess. For √18, a good starting point is 4.5.
- Use the formula: \(x_{n+1} = \frac{1}{2} \left( x_n + \frac{18}{x_n} \right)\).
- Plug in the initial guess: \(x_1 = \frac{1}{2} \left( 4.5 + \frac{18}{4.5} \right) = 4.25\).
- Repeat the process: \(x_2 = \frac{1}{2} \left( 4.25 + \frac{18}{4.25} \right) \approx 4.243\).
- Continue iterating until the values converge to a stable value. This method provides an approximation of √18 as approximately 4.2426.
These techniques are powerful tools for approximating square roots, allowing you to find values close to the actual square root even without a calculator.
Applications of Square Roots in Real Life
Square roots play a vital role in various real-life applications, spanning numerous fields and industries. Below are some of the significant applications of square roots in everyday life:
-
Finance:
In finance, square roots are used to calculate stock market volatility, which is a measure of how much a stock’s price varies over time. This calculation helps investors assess the risk associated with a particular investment.
-
Architecture and Engineering:
Square roots are crucial in determining the natural frequency of structures such as bridges and buildings, helping engineers predict how structures will react to different loads and forces.
-
Science:
Square roots are used in various scientific calculations, including determining the velocity of moving objects, the intensity of sound waves, and the amount of radiation absorbed by materials.
-
Statistics:
In statistics, square roots are used to calculate the standard deviation, which measures the amount of variation or dispersion in a set of data. This is crucial for analyzing data sets and making informed decisions.
-
Geometry:
Square roots are used to calculate the area and perimeter of shapes and to solve problems involving right triangles. The Pythagorean theorem, for example, uses square roots to determine the length of the sides of a right triangle.
-
Computer Science:
Square roots are used in computer programming for various applications, such as encryption algorithms, image processing, and game physics. These calculations are essential for developing secure and efficient software.
-
Cryptography:
Square roots are used in cryptography for creating secure communication channels and digital signatures. These applications are vital for protecting data and ensuring secure transactions.
-
Navigation:
In navigation, square roots are used to calculate distances between points on a map or globe, helping pilots and sailors determine the best routes and directions.
-
Electrical Engineering:
Square roots are used in electrical engineering to calculate power, voltage, and current in circuits. These calculations are essential for designing and maintaining electrical systems.
-
Photography:
In photography, the aperture of a camera lens is controlled by an f-number, which is related to the square root of the area of the aperture. Adjusting the f-number changes the amount of light entering the camera, affecting the exposure of the photograph.
-
Computer Graphics:
Square roots are used in computer graphics to calculate distances and lengths of vectors, which are essential for rendering images and animations in 2D and 3D graphics.
-
Telecommunication:
In telecommunication, signal strength decreases with the square of the distance from the transmitter, a concept known as the inverse square law. Understanding this relationship is crucial for designing efficient communication systems.

Practical Examples Involving √18
The square root of 18, denoted as √18 or 3√2, is approximately 4.24. This value has various practical applications in different fields. Here are some examples:
-
Geometry and Construction: In geometry, square roots are often used to find the length of the sides of squares and rectangles. For instance, if you have a square with an area of 18 square units, each side of the square would be √18 units long, which is approximately 4.24 units.
-
Physics: In physics, square roots are frequently used to solve equations involving area and distance. For example, if the kinetic energy of an object is related to its velocity squared, you might use the square root to solve for the velocity.
-
Statistics: In statistics, standard deviation, which measures the amount of variation or dispersion in a set of values, involves the use of square roots. If a dataset's variance is 18, then the standard deviation would be √18, approximately 4.24.
-
Engineering: Engineers use square roots in various calculations. For example, in electrical engineering, the root mean square (RMS) value of an alternating current (AC) is a type of average that involves square roots. If an AC voltage has a mean square value of 18, its RMS value would be √18 volts.
-
Astronomy: Astronomers use square roots to calculate distances in space. For example, the intensity of light from a star diminishes with the square of the distance from the observer, so calculating the distance involves using square roots.
-
Finance: In finance, the concept of volatility or the variability of asset prices is often expressed using standard deviation, which involves square roots. If the variance of returns on an investment is 18, the volatility would be √18, approximately 4.24.
These examples demonstrate how the square root of 18, although a simple mathematical concept, plays a crucial role in various real-world applications across different fields.
Common Mistakes and Misconceptions
Understanding square roots can sometimes be challenging, leading to common mistakes and misconceptions. Here, we address some of the frequent errors encountered when dealing with the square root of 18, helping you to avoid them in your calculations.
-
Incorrect Simplification: A common mistake is incorrectly simplifying √18. The correct simplification is:
\[\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}\]
However, some may mistakenly simplify it as \(\sqrt{9 + 2}\), which is incorrect.
-
Neglecting the Order of Operations: When working with square roots, it's essential to follow the proper order of operations. For example:
\[\sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\]
Neglecting to square the numbers before summing them would lead to incorrect results.
-
Misinterpreting Square Root Properties: Some misconceptions arise from misunderstanding the properties of square roots. For example:
\[\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\]
But this does not mean that \(\sqrt{a + b} = \sqrt{a} + \sqrt{b}\), which is a common error.
-
Ignoring Rational and Irrational Numbers: Another mistake is failing to recognize when a square root results in a rational or irrational number. For instance:
\[\sqrt{18}\] is an irrational number, but students might incorrectly approximate it as a simple fraction without proper precision.
-
Dividing by Zero: When manipulating square roots in equations, one must avoid dividing by zero. For example, solving:
\[ \frac{\sqrt{18}}{x} = \text{Undefined if } x = 0 \]
Ensuring \(x\) is non-zero is crucial to avoid undefined results.
By being aware of these common mistakes, students and professionals can enhance their understanding and accuracy when working with square roots, particularly with numbers like 18.
FAQs about Square Root of 18
Here are some frequently asked questions about the square root of 18:
-
What is the square root of 18?
The square root of 18 is expressed as √18 or 3√2. In decimal form, it is approximately 4.242640687.
-
Is the square root of 18 a rational number?
No, the square root of 18 is not a rational number. It is an irrational number because its decimal representation is non-terminating and non-repeating.
-
Can the square root of 18 be simplified?
Yes, the square root of 18 can be simplified to 3√2. This is because 18 can be factored into 9 and 2, where 9 is a perfect square.
-
What is the prime factorization of 18?
The prime factorization of 18 is 2 × 32. Using these factors, √18 can be simplified to 3√2.
-
Is -3√2 also a square root of 18?
Yes, -3√2 is also a square root of 18 because when it is squared, it gives 18.
-
How do you calculate the square root of 18 using the long division method?
To find the square root of 18 using the long division method:
- Write 18 as 18.000000 and group the digits in pairs starting from the decimal point.
- Find a number which, when squared, is less than or equal to 18. The number is 4 (since 42 = 16).
- Subtract 16 from 18 to get 2. Bring down the next pair of zeros to make it 200.
- Double the divisor (which is 4) to get 8 and find a number x such that 8x * x ≤ 200. The number is 2 (since 82 * 2 = 164).
- Repeat this process to get the decimal value up to the desired precision.
-
Can we use the repeated subtraction method to find the square root of 18?No, the repeated subtraction method can only be used for perfect squares, and since 18 is not a perfect square, this method is not applicable.
-
What is the significance of the square root of 18 in real life?
The square root of 18 can be useful in various practical applications, such as calculating areas and lengths in geometry, solving quadratic equations, and in various fields of science and engineering.
Conclusion
In conclusion, the square root of 18, denoted as \(\sqrt{18}\), is an interesting number with various properties and applications. Here are the key takeaways:
- Radical Form: The simplest radical form of the square root of 18 is \(3\sqrt{2}\).
- Decimal Form: The approximate value of \(\sqrt{18}\) in decimal form is 4.2426.
- Nature: \(\sqrt{18}\) is an irrational number because its decimal representation is non-terminating and non-repeating.
- Calculation Methods: There are several methods to calculate \(\sqrt{18}\), including prime factorization, the long division method, and using approximation techniques.
Understanding the square root of 18 helps in various mathematical contexts such as solving equations, geometry, and real-life applications like determining distances and areas. Mastery of these concepts not only strengthens mathematical foundations but also enhances problem-solving skills.
Whether calculated manually or using a calculator, the square root of 18 exemplifies the beauty of mathematics and its practical utility in our daily lives.

Tìm hiểu về căn bậc hai của 18 và cách tính toán, ứng dụng thực tế trong cuộc sống hàng ngày.
Căn bậc hai của 18
READ MORE:
Hướng dẫn cách đơn giản hóa căn bậc hai của 18 (√18) và áp dụng trong các bài toán thực tế.
Làm thế nào để đơn giản hóa căn bậc hai của 18: √18

