Topic square root of 18 in simplest radical form: Discover how to simplify the square root of 18 to its simplest radical form with our easy, step-by-step guide. Whether you're a student or just curious, this clear explanation will help you understand and master the concept effortlessly. Learn the process and boost your math skills today!
Table of Content
- Square Root of 18 in Simplest Radical Form
- Introduction to Square Roots
- Understanding Radical Expressions
- Prime Factorization Method
- Steps to Simplify the Square Root of 18
- Breaking Down the Radical
- Simplifying Radicals with Perfect Squares
- Combining Factors for the Simplest Form
- Mathematical Properties of Square Roots
- Practical Examples and Applications
- Frequently Asked Questions
- Conclusion
- YOUTUBE:
Square Root of 18 in Simplest Radical Form
The square root of 18 can be simplified to its simplest radical form using the following steps:
- First, identify the prime factors of 18. The prime factorization of 18 is:
\(18 = 2 \times 3 \times 3 = 2 \times 3^2\)
- Next, use the property of square roots that states \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\). Thus, we can break down \(\sqrt{18}\) as follows:
\(\sqrt{18} = \sqrt{2 \times 3^2}\)
- Then, separate the square root of the perfect square from the other factors:
\(\sqrt{18} = \sqrt{2} \times \sqrt{3^2}\)
- Since the square root of 3 squared is 3, we can simplify further:
\(\sqrt{18} = \sqrt{2} \times 3\)
- Finally, we rewrite the expression with the simplified form:
\(\sqrt{18} = 3\sqrt{2}\)
Therefore, the square root of 18 in its simplest radical form is:
READ MORE:
Introduction to Square Roots
Square roots are fundamental concepts in mathematics, representing a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, since \(4 \times 4 = 16\). Square roots are denoted by the radical symbol \(\sqrt{}\).
Understanding square roots involves recognizing both perfect squares and non-perfect squares. Perfect squares, like 1, 4, 9, 16, and 25, have whole number square roots. Non-perfect squares result in irrational numbers, which are often simplified into radical form.
To find the square root of a number:
- Prime Factorization: Break down the number into its prime factors.
- Group Factors: Pair the prime factors to simplify the square root.
- Simplify: Extract the square roots of the pairs and multiply them.
For instance, to simplify the square root of 18:
- Prime factorization: \(18 = 2 \times 3 \times 3 = 2 \times 3^2\).
- Group the factors: \(\sqrt{18} = \sqrt{2 \times 3^2}\).
- Simplify: \(\sqrt{18} = \sqrt{2} \times \sqrt{3^2} = 3\sqrt{2}\).
This method helps in understanding and simplifying square roots effectively, ensuring accurate mathematical computations and a deeper comprehension of number properties.
Understanding Radical Expressions
Radical expressions involve roots, most commonly square roots, and are a fundamental part of algebra. A radical expression is written with a radical symbol \(\sqrt{}\) and can include numbers, variables, or both. Understanding how to simplify and manipulate these expressions is crucial for solving various mathematical problems.
Here are the key steps to understanding and working with radical expressions:
- Identifying the Radicand: The number or expression inside the radical symbol is called the radicand. For example, in \(\sqrt{18}\), 18 is the radicand.
- Prime Factorization: Break down the radicand into its prime factors. This step is essential for simplifying the radical expression. For instance, \(18 = 2 \times 3^2\).
- Simplifying the Radical: Pair the prime factors and move them outside the radical symbol. Each pair of identical factors can be taken out of the radical. For example:
\(\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} = 3\sqrt{2}\).
- Combining Like Radicals: Similar to combining like terms in algebra, you can combine radicals with the same radicand. For instance, \(2\sqrt{2} + 3\sqrt{2} = 5\sqrt{2}\).
- Rationalizing the Denominator: When a radical expression has a radical in the denominator, multiply the numerator and the denominator by a value that will eliminate the radical from the denominator. For example:
\(\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\).
Understanding these principles allows for the accurate simplification and manipulation of radical expressions, enhancing problem-solving skills and mathematical comprehension.
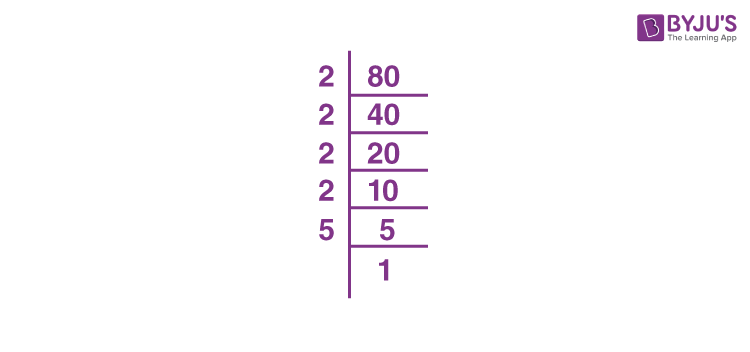
Prime Factorization Method
To simplify the square root of 18 using the prime factorization method, follow these detailed steps:
- Find the Prime Factors of 18:
Start by determining the prime factors of 18. A prime factor is a factor that is a prime number. The prime factors of 18 are:
- 18 divided by 2 (the smallest prime number) gives 9.
- 9 is then divided by 3 (the next smallest prime number), resulting in 3.
- 3 is a prime number, so we stop here.
Thus, the prime factorization of 18 is \(2 \times 3 \times 3\) or \(2 \times 3^2\).
- Rewrite the Square Root:
Express the square root of 18 using its prime factors:
\[\sqrt{18} = \sqrt{2 \times 3^2}\]
- Simplify the Radical:
Identify and separate the perfect square (in this case, \(3^2\)) from the radical:
\[\sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}\]
Simplify \(\sqrt{3^2}\) to 3:
\[\sqrt{2} \times 3 = 3\sqrt{2}\]
- Conclusion:
The square root of 18 in its simplest radical form is:
\[3\sqrt{2}\]
Steps to Simplify the Square Root of 18
To simplify the square root of 18, we can follow these detailed steps:
-
Factorize the Number 18:
First, we need to find the prime factors of 18. Since 18 is an even number, it is divisible by 2.
\[ 18 = 2 \times 9 \]
Next, we factor 9 into prime numbers:
\[ 9 = 3 \times 3 \]
So, the complete factorization of 18 is:
\[ 18 = 2 \times 3 \times 3 \]
-
Group the Factors:
We group the factors into pairs of squares where possible:
\[ \sqrt{18} = \sqrt{2 \times 3 \times 3} \]
-
Apply the Square Root Property:
We use the property of square roots which states that the square root of a product is equal to the product of the square roots:
\[ \sqrt{18} = \sqrt{2} \times \sqrt{3 \times 3} \]
-
Simplify the Expression:
We know that the square root of 9 (which is \(3 \times 3\)) is 3:
\[ \sqrt{3 \times 3} = 3 \]
Therefore, the expression simplifies to:
\[ \sqrt{18} = \sqrt{2} \times 3 = 3\sqrt{2} \]
So, the simplest radical form of the square root of 18 is \(3\sqrt{2}\).

Breaking Down the Radical
To simplify the square root of 18, we need to break down the radical into its prime factors. Here’s a detailed step-by-step method:
-
Identify the Prime Factors:
First, we find the prime factors of 18. We can do this by continuously dividing 18 by its smallest prime factors:
- 18 ÷ 2 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
So, the prime factors of 18 are 2 and 3. We can express 18 as:
\( 18 = 2 \times 3 \times 3 \)
-
Group the Prime Factors:
Next, we group the prime factors in pairs, where possible:
\( 18 = 2 \times 3^2 \)
-
Apply the Square Root:
We take the square root of both sides. Remember that the square root of a product is the product of the square roots:
\( \sqrt{18} = \sqrt{2 \times 3^2} \)
-
Simplify the Radical:
The square root of 32 is 3, so we can simplify the expression:
\( \sqrt{18} = 3 \sqrt{2} \)
Therefore, the simplest radical form of the square root of 18 is \( 3 \sqrt{2} \). This form is more concise and reveals the fundamental components of the number.
Using MathJax, the simplification can be visually represented as:
\[
\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}
\]
This step-by-step method allows us to clearly understand and simplify the square root of any number by breaking it down into its prime factors and simplifying accordingly.
Simplifying Radicals with Perfect Squares
Simplifying radicals, especially those that are not perfect squares, involves breaking them down using perfect squares. Here's a detailed, step-by-step process to simplify the square root of 18 using perfect squares:
-
Identify the Perfect Square Factors:
First, list the factors of 18 to find the perfect squares. The factors of 18 are 1, 2, 3, 6, 9, and 18. Among these, the perfect squares are 1 and 9.
-
Divide by the Largest Perfect Square:
Next, divide 18 by the largest perfect square from the list. Here, the largest perfect square is 9.
\[
18 \div 9 = 2
\] -
Write the Square Root as a Product:
Express the square root of 18 using the result from the division:
\[
\sqrt{18} = \sqrt{9 \times 2}
\] -
Simplify the Square Root of the Perfect Square:
Calculate the square root of 9, which is 3. Then, separate the square roots:
\[
\sqrt{18} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}
\]
Therefore, the simplest radical form of the square root of 18 is \(3\sqrt{2}\). This method ensures the radical is expressed in its most simplified form, making it easier to work with in further calculations.
In decimal form, the square root of 18 is approximately 4.2426, but in simplest radical form, it is expressed as \(3\sqrt{2}\).
Combining Factors for the Simplest Form
To simplify the square root of 18 to its simplest radical form, we need to combine its prime factors correctly. Here is a detailed step-by-step guide:
-
Prime Factorization:
First, we need to find the prime factors of 18. The prime factorization of 18 is:
\[ 18 = 2 \times 3 \times 3 \]
-
Group the Factors:
Next, we group the factors into pairs of equal factors under the square root:
\[ \sqrt{18} = \sqrt{2 \times 3 \times 3} \]
-
Identify and Simplify the Pairs:
We recognize that \(3 \times 3\) is a perfect square, which simplifies to \(3\). So, we pull out the perfect square from under the radical:
\[ \sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3 \]
-
Combine the Factors:
We then multiply the simplified factors outside the square root:
\[ \sqrt{18} = 3 \sqrt{2} \]
-
Final Simplified Form:
Therefore, the square root of 18 in its simplest radical form is:
\[ \sqrt{18} = 3 \sqrt{2} \]
By combining the factors in this way, we ensure that the expression is in its simplest radical form, making it easier to understand and use in further mathematical calculations.
Mathematical Properties of Square Roots
The mathematical properties of square roots are fundamental in simplifying radical expressions and understanding their behavior. Here are some key properties:
- Product Property: The square root of a product is equal to the product of the square roots of the factors.
\[\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\]
Example: \(\sqrt{18} = \sqrt{9 \cdot 2} = \sqrt{9} \cdot \sqrt{2} = 3\sqrt{2}\)
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator.
\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\]
Example: \(\sqrt{\frac{9}{4}} = \frac{\sqrt{9}}{\sqrt{4}} = \frac{3}{2}\)
- Square of a Square Root: The square of a square root returns the original number.
\[(\sqrt{a})^2 = a\]
Example: \((\sqrt{18})^2 = 18\)
- Square Root of a Square: The square root of a squared number returns the absolute value of the original number.
\[\sqrt{a^2} = |a|\]
Example: \(\sqrt{(-3)^2} = 3\)
- Adding and Subtracting Square Roots: Square roots can be added or subtracted if they have the same radicand (the number inside the radical).
\[a\sqrt{b} + c\sqrt{b} = (a + c)\sqrt{b}\]
Example: \(2\sqrt{2} + 3\sqrt{2} = 5\sqrt{2}\)
Understanding these properties helps in simplifying and solving expressions that involve square roots, making complex problems more manageable.

Practical Examples and Applications
Understanding how to simplify the square root of 18 can be very useful in various mathematical and real-world contexts. Here, we will explore several practical examples and applications of the simplest radical form of the square root of 18, which is \(3\sqrt{2}\).
-
Geometry and Measurements:
In geometry, the simplified form of square roots is often used to simplify the calculation of lengths, areas, and volumes. For example, if a right triangle has legs of lengths \(3\sqrt{2}\) and 3 units, the hypotenuse can be calculated using the Pythagorean theorem:
\[
\text{Hypotenuse} = \sqrt{(3\sqrt{2})^2 + 3^2} = \sqrt{18 + 9} = \sqrt{27} = 3\sqrt{3}
\] -
Physics and Engineering:
Square roots in their simplest form are also used in physics and engineering to simplify expressions involving energy, forces, and waves. For instance, in calculating the resultant force of two perpendicular forces, if one of the components is \(3\sqrt{2}\), using the simplest form makes the computation easier.
-
Statistics and Probability:
In statistics, the standard deviation and variance often involve square roots. Simplifying these can help in making the interpretation of data more straightforward. For instance, if the variance of a dataset is 18, the standard deviation is:
\[
\text{Standard Deviation} = \sqrt{18} = 3\sqrt{2}
\]
Step-by-Step Simplification
To understand the application, it's crucial to know the simplification process:
-
First, factorize the number 18: \(18 = 2 \times 3 \times 3\).
-
Next, identify pairs of prime factors: \(18 = 2 \times 3^2\).
-
Take the square root of the factor pairs: \(\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}\).
Applications in Algebra
When solving algebraic equations, simplifying square roots can make it easier to solve for variables. For instance, if you encounter an equation like \(x^2 = 18\), solving for \(x\) involves taking the square root of 18:
\[
x = \pm \sqrt{18} = \pm 3\sqrt{2}
\]
Thus, \(x = 3\sqrt{2}\) or \(x = -3\sqrt{2}\).
Mathematical Properties
Knowing that \(3\sqrt{2}\) is the simplest form of \(\sqrt{18}\) helps in understanding its properties:
- It is an irrational number.
- It cannot be expressed as a simple fraction.
- It appears in various mathematical contexts such as trigonometry and calculus.
By mastering the simplification of square roots, such as \(\sqrt{18} = 3\sqrt{2}\), you can enhance your mathematical problem-solving skills and apply these concepts effectively in diverse fields.
Frequently Asked Questions
Here are some common questions related to the square root of 18:
- Q: What is the simplest radical form of the square root of 18?
- Q: Is the square root of 18 a rational number?
- Q: Can we find the square root of 18 using the repeated subtraction method?
- Q: What is the decimal representation of the square root of 18?
- Q: What are the prime factors of 18?
- Q: What is the value of \(\sqrt{-18}\)?
- Q: How do we simplify the square root of 18 using the prime factorization method?
- Q: Is \(-3\sqrt{2}\) also a square root of 18?
A: The simplest radical form of the square root of 18 is \(3\sqrt{2}\).
A: No, the square root of 18 is not a rational number. It is an irrational number because it cannot be expressed as a simple fraction.
A: No, the repeated subtraction method is only applicable to perfect squares, and 18 is not a perfect square.
A: The decimal representation of the square root of 18 is approximately 4.2426.
A: The prime factorization of 18 is \(2 \times 3^2\).
A: The square root of -18 is an imaginary number and is expressed as \(3\sqrt{2}i\).
A: To simplify \(\sqrt{18}\), we factorize 18 as \(2 \times 3 \times 3\). We can then pair the 3s to get \(3\sqrt{2}\).
A: Yes, \(-3\sqrt{2}\) is also a square root of 18, since \((-3\sqrt{2})^2 = 18\).
Conclusion
The square root of 18 in its simplest radical form is \(3\sqrt{2}\). This result is derived through the process of simplifying the expression by identifying and utilizing the perfect squares within the factorization of the number 18. The steps involved include prime factorization, grouping the factors into pairs, and extracting the square root of those pairs to achieve the simplest form.
Understanding how to simplify square roots, such as \( \sqrt{18} \), is not only a valuable mathematical skill but also enhances comprehension of broader mathematical concepts. The simplified form \( 3\sqrt{2} \) highlights the elegance and efficiency of expressing roots in their most reduced form.
In practical applications, knowing the simplest radical form of a square root can simplify calculations and provide clearer insights, whether in academic problems, engineering tasks, or everyday situations. The value of \( \sqrt{18} \) being approximately 4.2426 in decimal form further connects abstract mathematical concepts with real-world measurements and applications.
In conclusion, the square root of 18 exemplifies the importance of mastering radical simplification techniques, enhancing both theoretical understanding and practical problem-solving abilities in mathematics.
Làm Thế Nào Để Đơn Giản Hóa Căn Bậc Hai của 18: Căn(18)
READ MORE:
Dạng Căn Bậc Đơn Giản Nhất