Topic how to simplify the square root of 18: Simplifying the square root of 18 may seem challenging, but with the right approach, it becomes easy and straightforward. In this guide, we will walk you through each step of the simplification process, ensuring you understand and master the technique. Unlock the simplicity behind square roots and boost your math skills today!
Table of Content
- Simplifying the Square Root of 18
- Introduction
- Understanding Square Roots
- Prime Factorization Method
- Step-by-Step Simplification Process
- Properties of Square Roots
- Examples and Practice Problems
- Common Mistakes to Avoid
- Advanced Simplification Techniques
- Applications of Simplified Square Roots
- YOUTUBE: Video hướng dẫn cách đơn giản hóa căn bậc hai của 18 một cách dễ hiểu và chi tiết.
Simplifying the Square Root of 18
To simplify the square root of 18, we need to find the prime factorization of 18 and then simplify using the properties of square roots.
Steps to Simplify \( \sqrt{18} \)
- Find the prime factorization of 18.
- Rewrite the square root of 18 using the prime factorization.
- Use the property of square roots to separate the factors.
- Simplify the square root of the perfect square.
- Combine the simplified terms.
18 can be factored into prime numbers as follows:
\( 18 = 2 \times 9 = 2 \times 3^2 \)
\( \sqrt{18} = \sqrt{2 \times 3^2} \)
\( \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} \)
\( \sqrt{3^2} = 3 \)
\( \sqrt{2} \times 3 = 3\sqrt{2} \)
Conclusion
Thus, the simplified form of \( \sqrt{18} \) is \( 3\sqrt{2} \).

READ MORE:
Introduction
The process of simplifying square roots is an essential skill in mathematics, providing a foundation for more advanced concepts. Simplifying the square root of 18 involves breaking down the number into its prime factors and applying the properties of square roots. This method not only makes calculations easier but also enhances your understanding of numerical relationships. In this guide, we will explore the step-by-step process of simplifying \( \sqrt{18} \) in a clear and comprehensive manner.
- Identify the prime factors of 18.
- Express 18 as a product of its prime factors.
- Rewrite the square root of 18 using its prime factorization.
- Separate the factors under the square root.
- Simplify the square root of the perfect square.
- Combine the simplified terms to get the final result.
By following these steps, you will be able to simplify \( \sqrt{18} \) to its simplest form, \( 3\sqrt{2} \), with confidence and ease.
Understanding Square Roots
Square roots are mathematical operations that allow us to determine a number which, when multiplied by itself, yields the original number. The square root of a number \( x \) is denoted as \( \sqrt{x} \). For example, the square root of 9 is 3, because \( 3 \times 3 = 9 \).
Square roots have several key properties that make them useful in various mathematical contexts:
- Non-negative results: The principal square root of a non-negative number is always non-negative.
- Perfect squares: If a number is a perfect square, its square root is an integer. For example, \( \sqrt{16} = 4 \).
- Product property: The square root of a product is the product of the square roots, i.e., \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \).
- Quotient property: The square root of a quotient is the quotient of the square roots, i.e., \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
Understanding these properties helps in simplifying complex square root expressions and solving equations involving square roots. For example, to simplify \( \sqrt{18} \), we can use the product property:
- Factor 18 into prime factors: \( 18 = 2 \times 3^2 \).
- Apply the product property: \( \sqrt{18} = \sqrt{2 \times 3^2} \).
- Separate the factors: \( \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} \).
- Simplify the square root of the perfect square: \( \sqrt{3^2} = 3 \).
- Combine the terms: \( \sqrt{18} = 3\sqrt{2} \).
By mastering these principles, you can tackle a wide range of mathematical problems involving square roots with confidence and accuracy.
Prime Factorization Method
The prime factorization method is a systematic approach to simplifying square roots by breaking down a number into its prime factors. This method helps in identifying perfect squares within the number, which can then be simplified. Here’s how to apply the prime factorization method to simplify \( \sqrt{18} \):
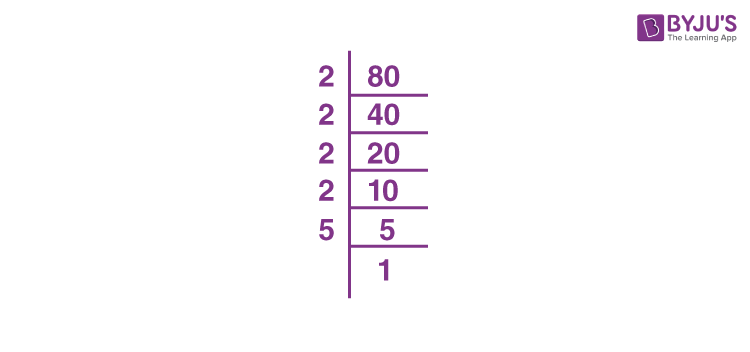
- Find the prime factors of 18:
- Start by dividing 18 by the smallest prime number, which is 2.
- \( 18 \div 2 = 9 \)
- Next, divide 9 by the smallest prime number, which is 3.
- \( 9 \div 3 = 3 \)
- Finally, divide 3 by 3.
- \( 3 \div 3 = 1 \)
So, the prime factorization of 18 is \( 2 \times 3 \times 3 \) or \( 2 \times 3^2 \).
- Rewrite the square root of 18 using its prime factorization:
\( \sqrt{18} = \sqrt{2 \times 3^2} \)
- Separate the factors under the square root:
Using the property of square roots, we can separate the factors:
\( \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} \)
- Simplify the square root of the perfect square:
\( \sqrt{3^2} = 3 \)
- Combine the simplified terms:
Multiply the simplified terms to get the final result:
\( \sqrt{2} \times 3 = 3\sqrt{2} \)
By following these steps, you can simplify \( \sqrt{18} \) to \( 3\sqrt{2} \) efficiently. This method can be applied to any number, making it a versatile tool in your mathematical toolkit.
Step-by-Step Simplification Process
To simplify the square root of 18, we can follow these steps:
- Identify the prime factors of 18.
- Express the square root in terms of its factors.
- Separate perfect squares from the square root.
- Simplify the square root by taking out the square roots of perfect squares.
Let's break down each step:
- First, find the prime factors of 18:
- 18 = 2 × 3 × 3
- Express the square root of 18 using its prime factors:
- √18 = √(2 × 3 × 3)
- Identify perfect squares within the square root:
- √18 = √(2 × 3²)
- Take out the square root of the perfect squares:
- √18 = 3√2
Therefore, the simplified form of √18 is 3√2.
Properties of Square Roots
When dealing with square roots, there are several key properties to keep in mind:
- Non-negative Numbers: The square root of a non-negative number is always a real number and is non-negative itself.
- Product Property: For any non-negative numbers \( a \) and \( b \), \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \).
- Quotient Property: For \( a \geq 0 \) and \( b > 0 \), \( \frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} \).
- Power Property: \( (\sqrt{a})^n = \sqrt{a^n} \) for even \( n \) and defined \( a \geq 0 \).
- Rationalization: Rationalizing the denominator involves multiplying by \( \frac{\sqrt{b}}{\sqrt{b}} \) to eliminate square roots from the denominator.
Examples and Practice Problems
To understand how to simplify the square root of 18, it's helpful to look at various examples and practice problems. Below, we will go through some detailed examples and provide practice problems to reinforce the concepts.
Example 1: Simplifying √18
- Start by factoring the number under the square root: \(18 = 2 \times 3 \times 3\).
- Group the prime factors into pairs: \(18 = 2 \times (3 \times 3)\).
- Take one number from each pair out of the square root: \(\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}\).
Example 2: Simplifying √72
- Factor the number: \(72 = 2 \times 2 \times 2 \times 3 \times 3\).
- Group the prime factors into pairs: \(72 = (2 \times 2) \times 2 \times (3 \times 3)\).
- Take one number from each pair out of the square root: \(\sqrt{72} = \sqrt{2^2 \times 3^2 \times 2} = 2 \times 3 \sqrt{2} = 6\sqrt{2}\).
Practice Problems
Try simplifying the following square roots:
- Simplify \(\sqrt{50}\)
- Simplify \(\sqrt{108}\)
- Simplify \(\sqrt{200}\)
Solutions:
- \(\sqrt{50} = \sqrt{2 \times 5 \times 5} = 5\sqrt{2}\)
- \(\sqrt{108} = \sqrt{2 \times 2 \times 3 \times 3 \times 3} = 6\sqrt{3}\)
- \(\sqrt{200} = \sqrt{2 \times 2 \times 2 \times 5 \times 5} = 10\sqrt{2}\)
Additional Practice
These additional problems will help you master simplifying square roots. Simplify the following:
- \(\sqrt{32}\)
- \(\sqrt{75}\)
- \(\sqrt{180}\)
These exercises provide a solid understanding of the steps involved in simplifying square roots. Keep practicing to improve your skills!
Common Mistakes to Avoid
When simplifying the square root of 18, it's important to be aware of common mistakes that can lead to incorrect results. Here are some pitfalls to avoid:
- Ignoring Prime Factorization: One of the most frequent mistakes is not breaking down the number completely into its prime factors. For √18, the prime factorization is 2 * 32, which helps in simplifying it correctly.
- Misidentifying Perfect Squares: It's crucial to correctly identify which numbers are perfect squares. For instance, √18 should be broken down as √(9 * 2) = √9 * √2 = 3√2. Incorrect identification can lead to wrong simplification.
- Incorrect Radical Simplification: Ensuring you simplify the radical properly without losing or adding factors is essential. For example, failing to recognize that √(9 * 2) simplifies to 3√2 can result in errors.
- Thinking Square Root is Division by Two: A common misconception is that finding the square root of a number is equivalent to dividing it by 2. For example, √16 is 4, not 8.
- Rewriting Radicand Incorrectly: When simplifying, ensure one of the factors is a perfect square. For example, √40 should be simplified as √(4 * 10) = 2√10, not just any two factors.
- Not Fully Simplifying: Always check for any remaining square factors in the radicand. For instance, √32 should be simplified fully to 4√2, not left as 2√8.
- Mixing Addition and Multiplication Laws: Remember the rules: for addition, only like radicals can be added (e.g., √3 + √3 = 2√3), while for multiplication, both numbers inside and outside the radicals are multiplied together (e.g., √3 * √3 = √9 = 3).
- Combining Unlike Radicals: Unlike radicals should not be combined. For example, √3 + √5 should remain as √3 + √5 and not be simplified further.
Avoiding these common mistakes will help you correctly simplify the square root of 18 and other similar radicals.
Advanced Simplification Techniques
When simplifying the square root of 18, several advanced techniques can be applied to achieve a more streamlined result. These methods are especially useful when dealing with more complex mathematical expressions or when higher precision is required. Below are some advanced techniques for simplifying square roots:
1. Prime Factorization Method
Prime factorization is a fundamental method for simplifying square roots, involving breaking down a number into its prime factors. For √18:
- Factorize 18 into prime numbers: \(18 = 2 \times 3^2\)
- Separate the perfect square: \( \sqrt{18} = \sqrt{2 \times 3^2} \)
- Simplify using the property \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \): \( \sqrt{18} = \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3 = 3\sqrt{2} \)
2. Rationalizing the Denominator
Rationalizing the denominator is a technique used to eliminate square roots from the denominator of a fraction:
For example, consider \( \frac{1}{\sqrt{18}} \):
- Multiply the numerator and denominator by \( \sqrt{18} \): \( \frac{1}{\sqrt{18}} \times \frac{\sqrt{18}}{\sqrt{18}} = \frac{\sqrt{18}}{18} \)
- Simplify the numerator using the prime factorization result: \( \frac{3\sqrt{2}}{18} = \frac{\sqrt{2}}{6} \)
3. Simplifying Fractions Under a Square Root
When dealing with square roots of fractions, use the rule \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \):
- Simplify \( \sqrt{\frac{18}{4}} \):
- Break it down: \( \sqrt{\frac{18}{4}} = \frac{\sqrt{18}}{\sqrt{4}} = \frac{3\sqrt{2}}{2} \)
4. Using Binomial Theorem
The binomial theorem can be used for approximating square roots, particularly useful when combined with other techniques for more complex expressions:
- Approximate \( \sqrt{18} \) as part of a binomial expression: \( (4 + 2)^{0.5} \approx 4^{0.5} \times (1 + \frac{2}{4})^{0.5} \)
- Further simplify the approximation: \( 2 \times (1 + 0.5)^{0.5} = 2 \times 1.22 = 2.44 \)
5. Logarithmic Simplification
Logarithms can also be applied to simplify the process of finding square roots:
- Express \( \sqrt{18} \) using natural logarithms: \( \sqrt{18} = e^{0.5 \ln(18)} \)
- Calculate the natural logarithm and exponentiate: \( \ln(18) \approx 2.89 \), thus \( e^{0.5 \times 2.89} \approx e^{1.445} \approx 4.24 \)
These advanced techniques offer various methods for simplifying square roots beyond basic prime factorization, providing deeper insights and more precise results in mathematical calculations.
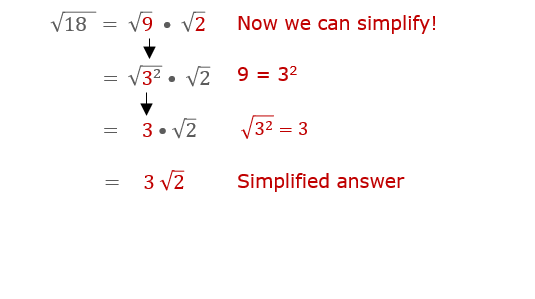
Applications of Simplified Square Roots
Simplified square roots are valuable in various fields, including:
- Geometry: Simplified square roots help in calculating side lengths and areas of geometric shapes, such as squares, rectangles, and triangles.
- Physics: They are crucial in equations involving distance, velocity, acceleration, and energy calculations.
- Engineering: Engineers use simplified square roots in structural analysis, especially for determining forces and stresses in materials.
- Finance: In financial mathematics, simplified square roots are used to calculate interest rates, investment returns, and risk assessments.
- Computer Science: Algorithms and calculations in programming often rely on simplified square roots for efficiency in computations.
Video hướng dẫn cách đơn giản hóa căn bậc hai của 18 một cách dễ hiểu và chi tiết.
Cách Đơn Giản Hóa Căn Bậc Hai Của 18: Căn(18)
READ MORE:
Video hướng dẫn cách tính và đơn giản hóa căn bậc hai của 18 một cách dễ hiểu và chi tiết.
Căn Bậc Hai Của 18