Simplify Square Root of 180: Easy Step-by-Step Guide

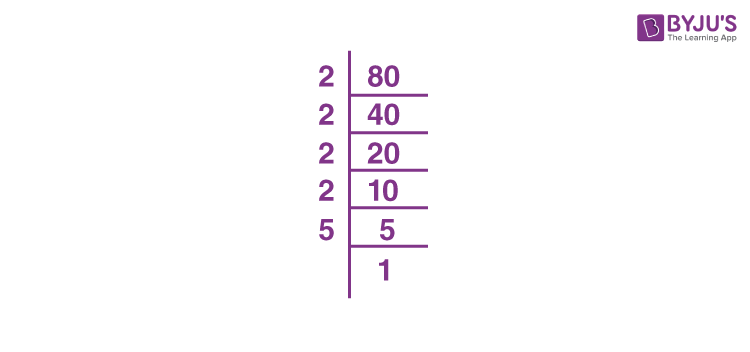
To simplify the square root of 180, we need to find the prime factorization of 180 and then simplify the square root by grouping the factors into pairs.

Step-by-Step Solution

1. Prime factorize 180:
   • 180 is even, so divide by 2: 180 ÷ 2 = 90
   • 90 is even, so divide by 2 again: 90 ÷ 2 = 45
   • 45 is divisible by 3: 45 ÷ 3 = 15
   • 15 is divisible by 3: 15 ÷ 3 = 5
   • 5 is a prime number

   So, the prime factorization of 180 is \( 2^2 \times 3^2 \times 5 \).

2. Rewrite the square root of 180 using its prime factors: \[ \sqrt{180} = \sqrt{2^2 \times 3^2 \times 5} \]
3. Group the factors into pairs and simplify:
   • The pairs are \( 2^2 \) and \( 3^2 \).
   • Take the square root of each pair: \( \sqrt{2^2} = 2 \) and \( \sqrt{3^2} = 3 \).
   • The factor 5 remains inside the square root: \( \sqrt{5} \).

   Therefore, we can simplify the expression as follows:
   \[
   \sqrt{180} = 2 \times 3 \times \sqrt{5} = 6\sqrt{5}
   \]

Final Simplified Form

The simplified form of the square root of 180 is \( 6\sqrt{5} \).

Simplifying square roots is a fundamental skill in mathematics that helps to express roots in their simplest form. This process involves breaking down a number into its prime factors and then simplifying the expression under the square root sign. Let's dive into the step-by-step method for simplifying the square root of 180.

1. Find the Prime Factorization of the Number:
   • Start by dividing the number by the smallest prime number (2) and continue the process until all factors are prime.
   • For 180:
     • 180 ÷ 2 = 90
     • 90 ÷ 2 = 45
     • 45 ÷ 3 = 15
     • 15 ÷ 3 = 5
     • 5 is a prime number

   The prime factorization of 180 is \( 2^2 \times 3^2 \times 5 \).

2. Rewrite the Square Root Using Prime Factors:

   Express the square root of 180 in terms of its prime factors:

   \[
   \sqrt{180} = \sqrt{2^2 \times 3^2 \times 5}
   \]

3. Simplify by Grouping Factors:
   • Identify pairs of prime factors: \( 2^2 \) and \( 3^2 \).
   • Take the square root of each pair: \( \sqrt{2^2} = 2 \) and \( \sqrt{3^2} = 3 \).
   • The factor 5 remains under the square root sign: \( \sqrt{5} \).

   Thus, the expression simplifies to:
   \[
   \sqrt{180} = 2 \times 3 \times \sqrt{5} = 6\sqrt{5}
   \]

By following these steps, you can simplify the square root of any number, making complex calculations more manageable and easier to understand.

A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3, because \( 3 \times 3 = 9 \). The square root symbol is \( \sqrt{} \). Understanding square roots is crucial for simplifying them and solving various mathematical problems.

Square roots have several properties that are helpful to know:

• The square root of a perfect square is an integer. For example, \( \sqrt{16} = 4 \).
• The square root of a non-perfect square is an irrational number. For example, \( \sqrt{2} \) is approximately 1.414.
• Square roots can be expressed in their simplest radical form by factoring the number under the root.

Steps to Simplify Square Roots

1. Identify Perfect Squares:

   Look for perfect square factors within the number. For instance, in the number 180, the perfect squares are 4 and 9.

2. Factor the Number:

   Break down the number into its prime factors and group the pairs of prime factors. For 180, the prime factorization is \( 2^2 \times 3^2 \times 5 \).

3. Rewrite Using Pairs:

   Rewrite the square root in terms of these factors:
   \[
   \sqrt{180} = \sqrt{2^2 \times 3^2 \times 5}
   \]

4. Simplify the Expression:

   Take the square root of the paired factors:
   \[
   \sqrt{2^2} = 2 \quad \text{and} \quad \sqrt{3^2} = 3
   \]

   Multiply these results and leave the remaining factor under the square root sign:
   \[
   2 \times 3 \times \sqrt{5} = 6\sqrt{5}
   \]

By understanding these steps, you can simplify any square root efficiently. The key is to recognize the factors and use properties of square roots to simplify the expression to its most manageable form.

The prime factorization method is an effective way to simplify square roots by breaking down the number into its prime factors. This method helps identify and simplify pairs of factors under the square root. Here’s a step-by-step guide to using the prime factorization method to simplify the square root of 180:

1. Factor the Number into Primes:

   Start by dividing the number by the smallest prime number and continue until all factors are prime:

   • 180 ÷ 2 = 90
   • 90 ÷ 2 = 45
   • 45 ÷ 3 = 15
   • 15 ÷ 3 = 5
   • 5 is a prime number

   The prime factorization of 180 is \( 2^2 \times 3^2 \times 5 \).

2. Rewrite the Square Root with Prime Factors:

   Express the square root of 180 using its prime factors:

   \[
   \sqrt{180} = \sqrt{2^2 \times 3^2 \times 5}
   \]

3. Group the Factors into Pairs:

   Identify pairs of prime factors that can be simplified:

   • Pair \( 2^2 \): \( \sqrt{2^2} = 2 \)
   • Pair \( 3^2 \): \( \sqrt{3^2} = 3 \)
4. Simplify the Expression:

   Take the square root of each pair and multiply them together, leaving any remaining factors inside the square root:

   \[
   2 \times 3 \times \sqrt{5} = 6\sqrt{5}
   \]

By using the prime factorization method, you can simplify the square root of 180 efficiently. This method is versatile and can be applied to any number, helping to break down complex square roots into more manageable forms.

To simplify the square root of 180, we will use the prime factorization method. Follow these detailed steps:

1. First, find the prime factorization of 180. Break it down into its prime factors:
   • 180 is even, so it can be divided by 2: \( 180 \div 2 = 90 \)
   • 90 is also even, so divide by 2 again: \( 90 \div 2 = 45 \)
   • 45 is not even, but it can be divided by 3: \( 45 \div 3 = 15 \)
   • 15 can be divided by 3 again: \( 15 \div 3 = 5 \)
   • 5 is a prime number.
   Thus, the prime factorization of 180 is \( 2 \times 2 \times 3 \times 3 \times 5 \) or \( 2^2 \times 3^2 \times 5 \).
2. Next, rewrite the square root of 180 using its prime factors:

   \( \sqrt{180} = \sqrt{2^2 \times 3^2 \times 5} \)

3. Separate the factors under the square root into pairs:

   \( \sqrt{2^2} \times \sqrt{3^2} \times \sqrt{5} \)

4. Simplify each pair of square roots:

   \( \sqrt{2^2} = 2 \) and \( \sqrt{3^2} = 3 \)

5. Combine the simplified factors:

   \( 2 \times 3 \times \sqrt{5} = 6\sqrt{5} \)

6. Thus, the simplified form of \( \sqrt{180} \) is:

   \( 6\sqrt{5} \)

When simplifying square roots, we aim to express the root in its simplest form. Here, we'll look at the square root of 180 and a few other examples to understand the process.

Example 1: Simplifying √180

1. Prime Factorization of 180:
   • 180 = 2 × 90
   • 90 = 2 × 45
   • 45 = 3 × 15
   • 15 = 3 × 5
   • Thus, 180 = 2² × 3² × 5
2. Group the pairs of prime factors:
   • √180 = √(2² × 3² × 5)
   • √180 = √(2²) × √(3²) × √5
3. Simplify the square roots of the pairs:
   • √180 = 2 × 3 × √5
   • √180 = 6√5

Thus, the simplified form of √180 is 6√5.

Example 2: Simplifying √72

1. Prime Factorization of 72:
   • 72 = 2 × 36
   • 36 = 2 × 18
   • 18 = 2 × 9
   • 9 = 3 × 3
   • Thus, 72 = 2³ × 3²
2. Group the pairs of prime factors:
   • √72 = √(2³ × 3²)
   • √72 = √(2² × 2) × √(3²)
3. Simplify the square roots of the pairs:
   • √72 = 2 × 3 × √2
   • √72 = 6√2

Thus, the simplified form of √72 is 6√2.

Example 3: Simplifying √50

1. Prime Factorization of 50:
   • 50 = 2 × 25
   • 25 = 5 × 5
   • Thus, 50 = 2 × 5²
2. Group the pairs of prime factors:
   • √50 = √(2 × 5²)
   • √50 = √2 × √(5²)
3. Simplify the square roots of the pairs:
   • √50 = 5√2

Thus, the simplified form of √50 is 5√2.

Example 4: Simplifying √200

1. Prime Factorization of 200:
   • 200 = 2 × 100
   • 100 = 2 × 50
   • 50 = 2 × 25
   • 25 = 5 × 5
   • Thus, 200 = 2³ × 5²
2. Group the pairs of prime factors:
   • √200 = √(2³ × 5²)
   • √200 = √(2² × 2) × √(5²)
3. Simplify the square roots of the pairs:
   • √200 = 2 × 5 × √2
   • √200 = 10√2

Thus, the simplified form of √200 is 10√2.

Simplifying square roots often involves identifying special cases that require unique handling. Here are some of these special cases:

1. Perfect Squares

When the radicand (the number under the square root) is a perfect square, the simplification is straightforward because the square root of a perfect square is an integer.

• \(\sqrt{25} = 5\)
• \(\sqrt{144} = 12\)

2. Prime Factorization Method

Sometimes, simplifying a square root requires breaking the number down into its prime factors, grouping the factors into pairs, and simplifying from there.

Example: Simplifying \(\sqrt{180}\)

1. Prime factorize 180: \(180 = 2^2 \times 3^2 \times 5\)
2. Group the pairs: \(\sqrt{180} = \sqrt{(2 \times 2) \times (3 \times 3) \times 5}\)
3. Take the square root of each pair: \(\sqrt{180} = 2 \times 3 \times \sqrt{5}\)
4. Simplify: \(\sqrt{180} = 6\sqrt{5}\)

3. Radicals Involving Fractions

Simplifying square roots that involve fractions can be handled by simplifying the numerator and the denominator separately.

Example: Simplifying \(\sqrt{\frac{9}{16}}\)

1. Separate the fraction: \(\sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}}\)
2. Simplify the numerator and the denominator: \(\frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4}\)
3. So, \(\sqrt{\frac{9}{16}} = \frac{3}{4}\)

4. Square Roots of Negative Numbers

Square roots of negative numbers introduce the concept of imaginary numbers. The imaginary unit \(i\) is defined as \(\sqrt{-1}\).

• \(\sqrt{-4} = 2i\)
• \(\sqrt{-9} = 3i\)

5. Multiplying and Dividing Square Roots

When multiplying or dividing square roots, you can often combine the radicands under a single radical sign and then simplify.

Example: \(\sqrt{3} \times \sqrt{12} = \sqrt{3 \times 12} = \sqrt{36} = 6\)

Example: \(\frac{\sqrt{50}}{\sqrt{2}} = \sqrt{\frac{50}{2}} = \sqrt{25} = 5\)

6. Adding and Subtracting Square Roots

Square roots can only be added or subtracted when they have the same radicand.

Example: \(\sqrt{8} + 2\sqrt{2} = \sqrt{4 \times 2} + 2\sqrt{2} = 2\sqrt{2} + 2\sqrt{2} = 4\sqrt{2}\)

Practice Problems

Try simplifying the following square roots:

• \(\sqrt{200}\)
• \(\sqrt{72}\)
• \(\sqrt{50} \times \sqrt{2}\)
• \(\sqrt{\frac{45}{5}}\)

Practice simplifying square roots with the following problems. Each problem is designed to help you apply the techniques for simplification step-by-step.

1. Simplify \(\sqrt{72}\):

   1. Find the prime factors of 72: \(72 = 2 \times 2 \times 2 \times 3 \times 3\).
   2. Group the prime factors into pairs: \(72 = (2 \times 2) \times (3 \times 3) \times 2 = 4 \times 9 \times 2\).
   3. Simplify the square root: \(\sqrt{72} = \sqrt{4 \times 9 \times 2} = \sqrt{4} \times \sqrt{9} \times \sqrt{2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\).

2. Simplify \(\sqrt{200}\):

   1. Find the prime factors of 200: \(200 = 2 \times 2 \times 2 \times 5 \times 5\).
   2. Group the prime factors into pairs: \(200 = (2 \times 2) \times (5 \times 5) \times 2 = 4 \times 25 \times 2\).
   3. Simplify the square root: \(\sqrt{200} = \sqrt{4 \times 25 \times 2} = \sqrt{4} \times \sqrt{25} \times \sqrt{2} = 2 \times 5 \times \sqrt{2} = 10\sqrt{2}\).

3. Simplify \(\sqrt{98}\):

   1. Find the prime factors of 98: \(98 = 2 \times 7 \times 7\).
   2. Group the prime factors into pairs: \(98 = 2 \times (7 \times 7) = 2 \times 49\).
   3. Simplify the square root: \(\sqrt{98} = \sqrt{2 \times 49} = \sqrt{2} \times \sqrt{49} = \sqrt{2} \times 7 = 7\sqrt{2}\).

4. Simplify \(\sqrt{450}\):

   1. Find the prime factors of 450: \(450 = 2 \times 3 \times 3 \times 5 \times 5\).
   2. Group the prime factors into pairs: \(450 = 2 \times (3 \times 3) \times (5 \times 5) = 2 \times 9 \times 25\).
   3. Simplify the square root: \(\sqrt{450} = \sqrt{2 \times 9 \times 25} = \sqrt{2} \times \sqrt{9} \times \sqrt{25} = \sqrt{2} \times 3 \times 5 = 15\sqrt{2}\).

5. Simplify \(\sqrt{500}\):

   1. Find the prime factors of 500: \(500 = 2 \times 2 \times 5 \times 5 \times 5\).
   2. Group the prime factors into pairs: \(500 = (2 \times 2) \times (5 \times 5) \times 5 = 4 \times 25 \times 5\).
   3. Simplify the square root: \(\sqrt{500} = \sqrt{4 \times 25 \times 5} = \sqrt{4} \times \sqrt{25} \times \sqrt{5} = 2 \times 5 \times \sqrt{5} = 10\sqrt{5}\).

Try simplifying these square roots and verify your answers using the methods outlined above. Regular practice will help you become more proficient in simplifying square roots.

When simplifying square roots, it's essential to be aware of common mistakes that can lead to incorrect solutions. Here are some frequent errors and tips to avoid them:

• Overlooking Perfect Squares: Not recognizing perfect squares within a square root can result in missed opportunities for simplification. Always check for perfect squares like 4, 9, 16, etc., within the radicand.
• Misapplying Properties: Incorrectly applying the product and quotient properties can lead to errors. For example, remember that √(a * b) = √a * √b, but √(a + b) ≠ √a + √b.
• Ignoring Variables: When dealing with variables, ensure you simplify them just as you would with numerical coefficients. For example, √(x^4) simplifies to x^2 because x^4 is a perfect square.
• Simplification Errors: Mistakes in arithmetic operations or incorrect factorization can lead to incorrect results. Double-check your work at each step to avoid such errors.
• Forgetting to Rationalize the Denominator: Leaving a square root in the denominator is often considered incomplete simplification. Always rationalize the denominator whenever possible, such as converting 1/√2 to √2/2.
• Ignoring Negative Solutions: When solving equations involving square roots, remember to consider both positive and negative solutions. For example, x^2 = 9 has solutions x = 3 and x = -3.
• Confusing Linear Properties: Remember that not all functions are linear. For instance, (x + y)^2 ≠ x^2 + y^2. This misconception can lead to incorrect simplifications.

By avoiding these common pitfalls, you can ensure more accurate and efficient simplification of square roots. Practice regularly and review your steps to become more confident in your mathematical abilities.

When simplifying square roots, there are several advanced techniques that can be employed to handle more complex problems efficiently. Below are some of these techniques:

1. Using Rational Exponents

Rational exponents provide an alternative method to simplify square roots. The square root of a number can be expressed as a power of one-half:

\[
\sqrt{a} = a^{1/2}
\]

This method can be extended to simplify roots of any degree.

2. Simplifying Products and Quotients Inside Radicals

By using the properties of radicals, you can simplify the square root of a product or a quotient:

• Product Rule: \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
• Quotient Rule: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)

3. Prime Factorization Method

The prime factorization method involves breaking down the number inside the square root into its prime factors and then simplifying. For example, to simplify \(\sqrt{180}\):

1. Factorize 180 into its prime factors: \(180 = 2^2 \times 3^2 \times 5\)
2. Group the prime factors into pairs: \(\sqrt{2^2 \times 3^2 \times 5}\)
3. Take the square root of each pair: \(2 \times 3 \times \sqrt{5} = 6\sqrt{5}\)

4. Long Division Method

The long division method is useful for finding square roots of non-perfect squares. Here is a step-by-step approach:

1. Pair the digits of the number starting from the decimal point.
2. Find the largest integer whose square is less than or equal to the first pair. Subtract the square from the pair.
3. Bring down the next pair of digits. Double the quotient and use it as a new divisor.
4. Continue this process until you have the desired level of precision.

This method is particularly useful for large numbers or when a high degree of accuracy is required.

5. Repeated Subtraction Method

This method involves repeatedly subtracting successive odd numbers from the original number until the remainder is zero or negative. If the remainder is zero, the number is a perfect square:

1. Start with 180 and subtract 1, then 3, then 5, and so on.
2. Continue the subtraction until the result is zero or negative.

If the result is zero, the number is a perfect square; otherwise, it is not. For 180, the subtraction will not result in zero, confirming that it is not a perfect square.

6. Using Technology

Advanced calculators and software can perform square root simplifications and verify results quickly. Tools like Mathway and calculators provided by various educational websites can simplify complex roots in seconds.

By employing these advanced techniques, you can simplify square roots more efficiently and tackle a wider range of mathematical problems.

Simplifying square roots is not just an academic exercise; it has practical applications in various real-life scenarios. Here are some examples:

1. Geometry and Construction

In construction, architects and engineers often use square roots to calculate distances and lengths. For example, the diagonal of a square with side length \(s\) can be found using the formula \( \sqrt{2s^2} = s\sqrt{2} \). This is essential for determining the correct length of materials needed for projects like bridges or buildings.

2. Physics and Gravity

Square roots are used in physics, particularly in equations involving gravity. The time \(t\) it takes for an object to fall from a height \(h\) is given by \( t = \frac{\sqrt{h}}{4} \). For instance, if an object is dropped from a height of 64 feet, it takes \( t = \frac{\sqrt{64}}{4} = 2 \) seconds to reach the ground.

3. Distance Between Points

In both two-dimensional and three-dimensional spaces, the distance between two points is calculated using the Pythagorean theorem, which involves square roots. The distance \(D\) between points \((x_1, y_1)\) and \((x_2, y_2)\) is \( D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \). This is widely used in fields such as navigation, astronomy, and even video game design to determine the shortest path between two points.

4. Quadratic Equations

Simplified square roots are crucial in solving quadratic equations, which are common in various scientific and engineering problems. The quadratic formula \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \) requires taking the square root of the discriminant \(b^2 - 4ac\) to find the roots of the equation.

5. Accident Investigation

Police use square roots to calculate the speed of vehicles involved in accidents based on the length of skid marks. For example, if the skid marks are \(d\) feet long, the speed \(v\) of the car can be approximated by \( v = \sqrt{24d} \). If the skid marks are 190 feet long, the speed is \( v = \sqrt{24 \times 190} \approx 67.5 \) mph.

6. Areas and Perimeters

In problems involving the area of squares, finding the side length requires taking the square root of the area. For example, if a square patio has an area of 200 square feet, each side would be \( \sqrt{200} \approx 14.1 \) feet.

These applications show how understanding and simplifying square roots can provide practical solutions to everyday problems and complex scientific calculations.

Simplifying square roots, such as the square root of 180, involves breaking down the number into its prime factors and then simplifying it by grouping and removing perfect squares from under the radical sign. This process helps in obtaining a simplified form which is often easier to work with in various mathematical applications.

For example, the square root of 180 can be simplified as follows:

• Prime factorize 180 to get \(180 = 2^2 \times 3^2 \times 5\).
• Group the perfect squares: \( \sqrt{180} = \sqrt{(2 \times 2) \times (3 \times 3) \times 5} \).
• Simplify to \(2 \times 3 \times \sqrt{5} = 6\sqrt{5}\).

This simplified form, \(6\sqrt{5}\), is often more useful in calculations and practical applications because it is more concise and easier to handle than the original radical form.

Understanding how to simplify square roots is a fundamental skill in mathematics that has real-world applications. For instance, in geometry, simplifying square roots can help in calculating distances, areas, and in solving various equations involving radicals.

In conclusion, mastering the technique of simplifying square roots enhances mathematical problem-solving skills and provides a strong foundation for more advanced mathematical concepts. Practice regularly with different numbers to become proficient in this essential skill.

Here are some common questions and answers related to simplifying square roots:

• Q1: How do I simplify the square root of 180?

  To simplify \(\sqrt{180}\), start with the prime factorization of 180:

  \[
  180 = 2^2 \times 3^2 \times 5
  \]

  Then, apply the product rule for square roots:

  \[
  \sqrt{180} = \sqrt{2^2 \times 3^2 \times 5} = \sqrt{2^2} \times \sqrt{3^2} \times \sqrt{5} = 2 \times 3 \times \sqrt{5} = 6\sqrt{5}
  \]

• Q2: Can I add square roots with different radicands?

  No, you can only add or subtract square roots with the same radicand. For example:

  \[
  3\sqrt{2} + 4\sqrt{2} = 7\sqrt{2}
  \]

  However, you cannot combine \( \sqrt{2} \) and \( \sqrt{3} \) directly.

• Q3: How do I handle square roots of fractions?

  You can simplify square roots of fractions using the rule:

  \[
  \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
  \]

  For example:

  \[
  \sqrt{\frac{25}{9}} = \frac{\sqrt{25}}{\sqrt{9}} = \frac{5}{3}
  \]

• Q4: What is a surd?

  A surd is an irrational root that cannot be simplified to a whole number. For example, \(\sqrt{3}\) is a surd, while \(\sqrt{4} = 2\) is not.

• Q5: How do I simplify square roots with variables?

  Apply the same principles to variables. For example:

  \[
  \sqrt{50x^2} = \sqrt{25 \times 2 \times x^2} = \sqrt{25} \times \sqrt{2} \times \sqrt{x^2} = 5x\sqrt{2}
  \]