Topic 18 square root: The square root of 18 is a captivating mathematical concept that opens doors to various intriguing applications and properties. In this article, we will delve into the methods of calculating, simplifying, and applying \(\sqrt{18}\) in real life, providing a comprehensive understanding of its significance and utility.
Table of Content
- Square Root of 18
- Introduction to Square Roots
- Understanding the Square Root of 18
- Methods to Calculate the Square Root of 18
- Approximation Techniques for \(\sqrt{18}\)
- Simplifying \(\sqrt{18}\)
- Properties of \(\sqrt{18}\)
- Mathematical Proofs Involving \(\sqrt{18}\)
- Applications of \(\sqrt{18}\) in Real Life
- Visual Representations of \(\sqrt{18}\)
- Frequently Asked Questions about \(\sqrt{18}\)
- YOUTUBE: Tìm hiểu cách đơn giản hóa căn bậc hai của 18 (Sqrt(18)) trong video này. Chúng tôi hướng dẫn từng bước để hiểu và áp dụng các phương pháp hiệu quả nhất.
Square Root of 18
The square root of 18 is a mathematical value that, when multiplied by itself, gives the number 18. This can be expressed using the square root symbol as follows:
Calculating the Square Root of 18
The square root of 18 is an irrational number, meaning it cannot be expressed exactly as a simple fraction. However, it can be approximated using various methods such as long division, estimation, or using a calculator.
The approximate value of \(\sqrt{18}\) is:
\(\sqrt{18} \approx 4.242640687\)
Simplifying the Square Root of 18
The square root of 18 can be simplified by expressing 18 as the product of its prime factors. This helps in breaking down the square root into simpler components:
\[ \sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2} \]
Properties of the Square Root of 18
- Irrational Number: \(\sqrt{18}\) cannot be expressed as a ratio of two integers.
- Positive and Negative Roots: The square root function has both a positive and a negative root. Hence, \(\sqrt{18}\) can be both \(+4.242640687\) and \(-4.242640687\).
Applications of the Square Root of 18
The square root of 18 is used in various mathematical calculations and applications, including geometry, algebra, and in real-life contexts where approximations are required. It is also used in solving quadratic equations and in various engineering and physics problems.
Visual Representation
To provide a visual understanding, plotting the function \(y = \sqrt{x}\) can help. At \(x = 18\), the value of \(y\) will be approximately 4.242640687.
Table of Values
Here is a small table showing values of the square root function around 18:
| x | \(\sqrt{x}\) |
|---|---|
| 16 | 4 |
| 17 | 4.1231056256 |
| 18 | 4.242640687 |
| 19 | 4.358898944 |
| 20 | 4.472135954 |
Conclusion
The square root of 18 is an important mathematical concept with various applications. Its simplified form is \(3\sqrt{2}\), and its approximate decimal value is 4.242640687.

READ MORE:
Introduction to Square Roots
Square roots are fundamental mathematical operations that are widely used in various fields. The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical symbol \(\sqrt{}\).
For example, the square root of 9 is 3 because \(3 \times 3 = 9\). Similarly, the square root of 16 is 4 because \(4 \times 4 = 16\). This concept can be extended to any non-negative number.
To better understand square roots, consider the following properties:
- Non-Negative Results: The square root of a non-negative number is also non-negative.
- Square of Square Roots: The square of the square root of a number returns the original number, i.e., \((\sqrt{a})^2 = a\).
- Product Property: The square root of a product is the product of the square roots, i.e., \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\).
- Quotient Property: The square root of a quotient is the quotient of the square roots, i.e., \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
Square roots can also be represented in decimal form, which is particularly useful for approximations. For instance, the square root of 2 is approximately 1.414, and the square root of 3 is approximately 1.732.
Calculating square roots can be performed using several methods:
- Prime Factorization: Break down the number into its prime factors and simplify.
- Long Division Method: A step-by-step approach similar to traditional division.
- Using Calculators: Modern calculators and computers can quickly compute square roots.
Understanding square roots is essential for solving quadratic equations, working with geometric shapes, and analyzing scientific data. They play a crucial role in various mathematical and real-world applications.
Understanding the Square Root of 18
The square root of 18 is an intriguing mathematical concept with significant importance in various calculations and applications. Represented as \(\sqrt{18}\), it is the value that, when multiplied by itself, yields 18.
The exact value of \(\sqrt{18}\) is an irrational number, meaning it cannot be expressed as a simple fraction. Its approximate decimal value is:
\(\sqrt{18} \approx 4.242640687\)
To simplify \(\sqrt{18}\), we can use its prime factorization:
- Factorize 18 into its prime factors: \(18 = 2 \times 3 \times 3\) or \(18 = 2 \times 3^2\).
- Apply the square root to the factorized form: \(\sqrt{18} = \sqrt{2 \times 3^2}\).
- Simplify by taking the square root of the perfect square: \(\sqrt{18} = \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3 = 3\sqrt{2}\).
Thus, the simplified form of \(\sqrt{18}\) is \(3\sqrt{2}\).
The properties of \(\sqrt{18}\) include:
- Irrational Number: \(\sqrt{18}\) cannot be exactly expressed as a fraction.
- Positive and Negative Roots: The square root of 18 has both positive and negative values: \(\pm \sqrt{18} \approx \pm 4.242640687\).
To illustrate the value of \(\sqrt{18}\), consider the following table of nearby square roots:
| x | \(\sqrt{x}\) |
|---|---|
| 16 | 4 |
| 17 | 4.1231056256 |
| 18 | 4.242640687 |
| 19 | 4.358898944 |
| 20 | 4.472135954 |
Understanding \(\sqrt{18}\) is crucial for solving equations, performing geometric calculations, and applying mathematical concepts in science and engineering. Its approximate value, simplified form, and properties make it a valuable tool in various mathematical contexts.
Methods to Calculate the Square Root of 18
Calculating the square root of 18 can be accomplished through several methods. Here, we outline three common techniques: prime factorization, long division, and using a calculator.
1. Prime Factorization Method
- Begin by factorizing 18 into its prime factors:
\(18 = 2 \times 3 \times 3\) or \(18 = 2 \times 3^2\).
- Apply the square root to the factorized form:
\(\sqrt{18} = \sqrt{2 \times 3^2}\).
- Simplify by taking the square root of the perfect square:
\(\sqrt{18} = \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3 = 3\sqrt{2}\).
The simplified form of \(\sqrt{18}\) is \(3\sqrt{2}\), which is approximately 4.242640687.
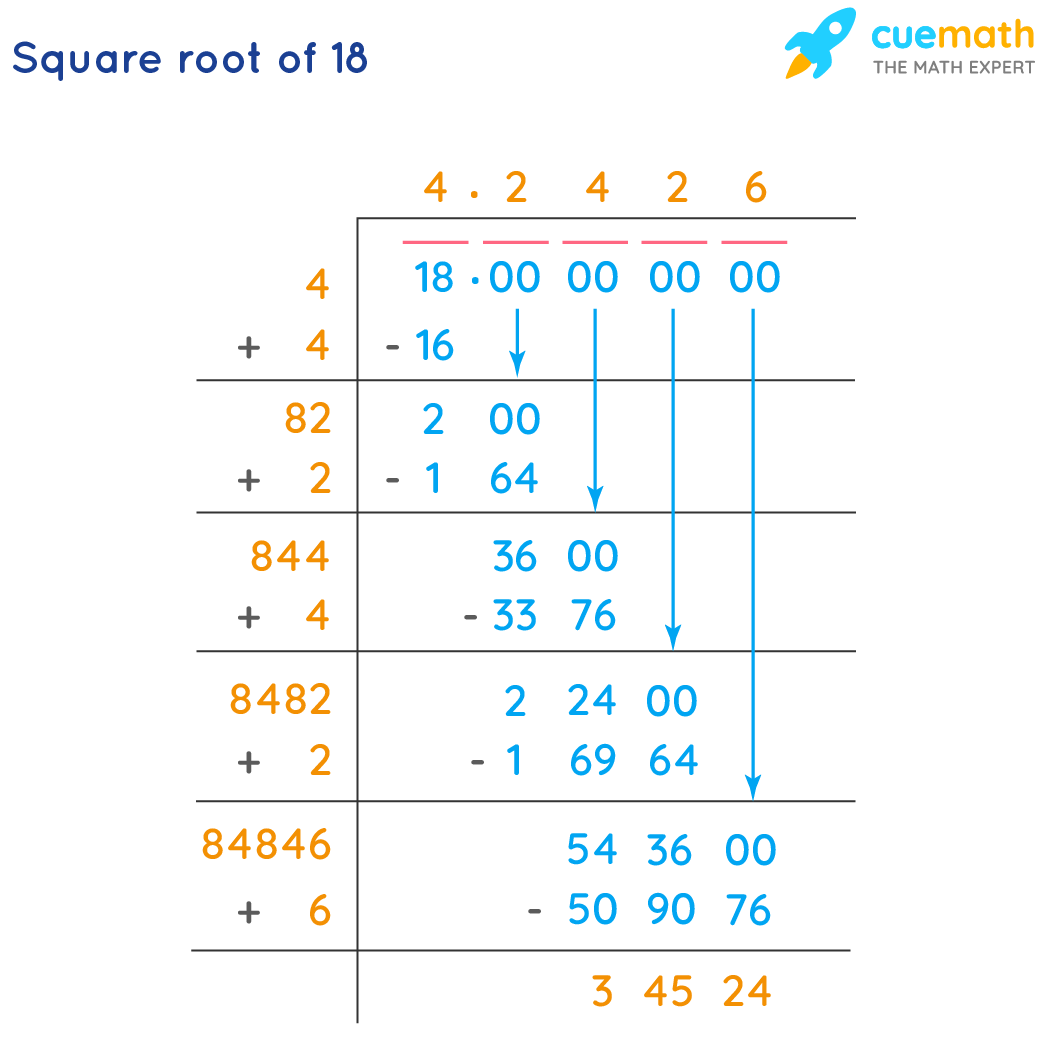
2. Long Division Method
The long division method provides a step-by-step approach to manually finding the square root of 18:
- Group the digits of 18 in pairs from right to left. For 18, we only have one group: 18.
- Find the largest integer (y) whose square (y^2) is less than or equal to the first group. Here, \(4^2 = 16\) is less than 18.
- Subtract \(y^2\) from the first group and bring down the next pair of digits (if any). For 18, we get 2 after subtracting 16 from 18.
- Double the current quotient (4) and determine the next digit (x) such that \(8x \times x\) is less than or equal to the new number (200). The next digit is 2, and \(82 \times 2 = 164\).
- Repeat the process for more digits to get a more accurate value. The approximate value obtained is 4.2426.
3. Using a Calculator
Using a calculator is the quickest method to find the square root of 18. Simply enter 18 and press the square root button (\(\sqrt{}\)) to get the result:
\(\sqrt{18} \approx 4.242640687\)
These methods provide different approaches to calculating the square root of 18, each with its own advantages. Whether simplifying using prime factorization, manually calculating through long division, or quickly finding the value with a calculator, understanding these methods enhances your mathematical proficiency.
Approximation Techniques for \(\sqrt{18}\)
Approximating the square root of 18 is useful when an exact value is not required, and it can be done through several techniques. Here, we discuss three common methods: the Babylonian method, estimation, and using a calculator.
1. Babylonian Method (Heron's Method)
The Babylonian method, also known as Heron's method, is an iterative technique for approximating square roots:
- Make an initial guess for \(\sqrt{18}\). Let's use 4.5.
- Use the formula: \[ \text{New guess} = \frac{\text{Old guess} + \frac{18}{\text{Old guess}}}{2} \]
- Apply the formula:
First iteration: \(\frac{4.5 + \frac{18}{4.5}}{2} = \frac{4.5 + 4}{2} = \frac{8.5}{2} = 4.25\)
Second iteration: \(\frac{4.25 + \frac{18}{4.25}}{2} = \frac{4.25 + 4.235294}{2} \approx 4.242647\)
Continue iterating until the desired accuracy is achieved. Each iteration brings you closer to the exact value.
2. Estimation Technique
Estimation provides a quick way to approximate \(\sqrt{18}\) by comparing it to known square roots:
- Recognize that \(\sqrt{16} = 4\) and \(\sqrt{25} = 5\).
- Since 18 is closer to 16 than 25, \(\sqrt{18}\) is slightly more than 4.
- Use linear interpolation between \(\sqrt{16}\) and \(\sqrt{25}\):
\(\sqrt{18} \approx 4 + \frac{18 - 16}{25 - 16} = 4 + \frac{2}{9} \approx 4.222\)
3. Using a Calculator
A calculator provides a quick and accurate approximation for \(\sqrt{18}\):
Simply enter 18 and press the square root button (\(\sqrt{}\)) to get the result:
\(\sqrt{18} \approx 4.242640687\)
To illustrate the approximation, consider the following table of values obtained through these methods:
| Method | Approximate Value |
|---|---|
| Babylonian (after 2 iterations) | 4.242647 |
| Estimation | 4.222 |
| Calculator | 4.242640687 |
These approximation techniques for \(\sqrt{18}\) offer various levels of accuracy and ease of use, making it possible to find a suitable method for different situations.

Simplifying \(\sqrt{18}\)
Simplifying the square root of 18 involves expressing it in the simplest radical form. This process helps in understanding its value better and making calculations easier. Follow these steps to simplify \(\sqrt{18}\):
- Find the prime factorization of 18:
\(18 = 2 \times 3 \times 3\) or \(18 = 2 \times 3^2\)
- Rewrite the square root using the prime factors:
\(\sqrt{18} = \sqrt{2 \times 3^2}\)
- Simplify the expression by taking the square root of the perfect square:
\(\sqrt{18} = \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3\)
- Combine the terms:
\(\sqrt{18} = 3\sqrt{2}\)
The simplified form of \(\sqrt{18}\) is \(3\sqrt{2}\). This means that the square root of 18 can be expressed as three times the square root of 2.
To verify, let's compare the decimal values:
- \(\sqrt{18} \approx 4.242640687\)
- \(3\sqrt{2} \approx 3 \times 1.414213562 = 4.242640686\)
The values match, confirming that \(3\sqrt{2}\) is the simplified form of \(\sqrt{18}\).
Understanding this simplification process is beneficial for various mathematical applications, such as solving equations and performing operations involving radicals. Simplified forms are easier to work with and often lead to more straightforward solutions.
Properties of \(\sqrt{18}\)
The square root of 18, denoted as \(\sqrt{18}\), has several interesting properties that are useful in mathematical calculations and problem-solving. Here, we explore these properties in detail.
1. Irrational Number
\(\sqrt{18}\) is an irrational number, which means it cannot be expressed as a simple fraction. Its decimal representation is non-terminating and non-repeating:
\(\sqrt{18} \approx 4.242640687\)
2. Simplified Form
The simplified form of \(\sqrt{18}\) is \(3\sqrt{2}\). This simplification is achieved through prime factorization:
\(18 = 2 \times 3^2\)
\(\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}\)
3. Positive and Negative Roots
Like all square roots, \(\sqrt{18}\) has both positive and negative values:
- Positive root: \(\sqrt{18} \approx 4.242640687\)
- Negative root: \(-\sqrt{18} \approx -4.242640687\)
4. Product Property
The square root of a product is the product of the square roots of the factors:
\(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
For \(\sqrt{18}\), this property can be illustrated as:
\(\sqrt{18} = \sqrt{2 \times 9} = \sqrt{2} \times \sqrt{9} = \sqrt{2} \times 3 = 3\sqrt{2}\)
5. Quotient Property
The square root of a quotient is the quotient of the square roots of the numerator and denominator:
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
For example:
\(\sqrt{\frac{18}{1}} = \frac{\sqrt{18}}{\sqrt{1}} = \frac{3\sqrt{2}}{1} = 3\sqrt{2}\)
6. Exponentiation Property
Square roots can be expressed as exponents:
\(\sqrt{a} = a^{1/2}\)
For \(\sqrt{18}\):
\(\sqrt{18} = 18^{1/2}\)
7. Conjugates
The conjugate of \(\sqrt{18}\) is useful in rationalizing denominators. For example:
If you have \(\frac{1}{\sqrt{18}}\), multiply by the conjugate \(\sqrt{18}\):
\(\frac{1}{\sqrt{18}} \times \frac{\sqrt{18}}{\sqrt{18}} = \frac{\sqrt{18}}{18} = \frac{3\sqrt{2}}{18} = \frac{\sqrt{2}}{6}\)
8. Application in Geometry
In geometry, \(\sqrt{18}\) can represent the diagonal length of a square with a side length of \(\sqrt{9}\) (or 3 units), given by the Pythagorean theorem:
\(d = \sqrt{3^2 + 3^2} = \sqrt{9 + 9} = \sqrt{18}\)
Understanding these properties of \(\sqrt{18}\) helps in various mathematical and practical applications, making calculations more manageable and insights more profound.
Mathematical Proofs Involving \(\sqrt{18}\)
To explore the mathematical properties and proofs involving \(\sqrt{18}\), we can use several methods, including direct calculation, algebraic manipulation, and properties of irrational numbers.
Direct Calculation Using Prime Factorization
First, we find the prime factorization of 18:
- 18 can be factored into 2 and 9.
- 9 can be further factored into 3 and 3.
So, the prime factorization of 18 is \(2 \times 3^2\). Using this, we can simplify \(\sqrt{18}\):
\[
\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3 = 3\sqrt{2}
\]
Algebraic Proof of Irrationality
We can prove that \(\sqrt{18}\) is irrational using a contradiction method. Assume \(\sqrt{18}\) is rational, meaning it can be expressed as a fraction \(\frac{p}{q}\) where \(p\) and \(q\) are coprime integers and \(q \neq 0\). Then:
\[
\sqrt{18} = \frac{p}{q}
\]
Squaring both sides gives:
\[
18 = \frac{p^2}{q^2} \implies 18q^2 = p^2
\]
This equation shows that \(p^2\) is divisible by 18. Hence, \(p\) must be divisible by 3 (since 3 is a prime factor of 18). Let \(p = 3k\) for some integer \(k\). Substituting back into the equation gives:
\[
18q^2 = (3k)^2 \implies 18q^2 = 9k^2 \implies 2q^2 = k^2
\]
This implies \(k^2\) is even, meaning \(k\) must be even. Let \(k = 2m\). Substituting back, we get:
\[
2q^2 = (2m)^2 \implies 2q^2 = 4m^2 \implies q^2 = 2m^2
\]
This implies \(q^2\) is even, meaning \(q\) is even. But this contradicts the assumption that \(p\) and \(q\) are coprime (since both would be divisible by 2). Therefore, \(\sqrt{18}\) is irrational.
Properties of \(\sqrt{18}\)
Some properties of \(\sqrt{18}\) include:
- \(\sqrt{18}\) is an irrational number, as shown above.
- \(\sqrt{18}\) can be simplified to \(3\sqrt{2}\).
- It lies between 4 and 5, more precisely, it is approximately 4.2426.
Example Proof Using Quadratic Equations
Let's consider the quadratic equation \(x^2 - 18 = 0\). The roots of this equation are:
\[
x = \pm \sqrt{18}
\]
Using the quadratic formula \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\) with \(a = 1\), \(b = 0\), and \(c = -18\), we get:
\[
x = \frac{0 \pm \sqrt{0^2 - 4 \cdot 1 \cdot (-18)}}{2 \cdot 1} = \frac{\pm \sqrt{72}}{2} = \pm \sqrt{18}
\]
Conclusion
The square root of 18 can be explored through various proofs and methods. It highlights important concepts in algebra and number theory, such as simplification, irrationality, and quadratic equations.
Applications of \(\sqrt{18}\) in Real Life
The square root of 18, approximately 4.24, finds various practical applications in real life. Here are some key examples:
- Geometry and Construction:
When dealing with areas and lengths, square roots are essential. For instance, if you have a square with an area of 18 square units, each side will be \(\sqrt{18}\) units long. This is useful in designing and constructing various elements like patios, gardens, and rooms where specific area measurements are crucial.
- Physics and Gravity:
In physics, the square root function is used to determine the time it takes for an object to fall to the ground from a certain height. For example, the time \(t\) (in seconds) it takes for an object to fall from a height \(h\) (in feet) can be approximated by the formula \( t = \frac{\sqrt{h}}{4} \). If an object is dropped from a height of 18 feet, it would take approximately \( t = \frac{\sqrt{18}}{4} \approx 1.06 \) seconds to reach the ground.
- Accident Investigations:
Police often use square roots to determine the speed of a vehicle before it stopped. By measuring the length of skid marks and applying the appropriate formula, they can estimate the speed. For example, if the skid marks are 18 feet long, using a simplified formula, the speed \(v\) can be approximated as \( v = \sqrt{24 \times 18} \approx 20.78 \) miles per hour.
- Architecture and Design:
Architects use square roots to calculate various dimensions and ensure the structural integrity of their designs. For example, when designing a feature with a diagonal length of \(\sqrt{18}\) meters, they ensure that all measurements are accurate for the desired aesthetic and structural outcomes.
These examples highlight how the mathematical concept of square roots, including \(\sqrt{18}\), is applied in various fields to solve real-world problems effectively.
Visual Representations of \(\sqrt{18}\)
Visualizing the square root of 18 can help in understanding its value and properties more effectively. Here are some common visual representations:
1. Number Line Representation
One way to represent \(\sqrt{18}\) is on a number line. Since \(\sqrt{18} \approx 4.24\), it is located between the integers 4 and 5. This visual helps to see where \(\sqrt{18}\) lies in relation to other whole numbers.
2. Geometric Representation
Geometrically, \(\sqrt{18}\) can be represented as the diagonal of a square with side length 3\(\sqrt{2}\). Here, each side of the square is scaled to illustrate the approximate length of \(\sqrt{18}\).
3. Simplification Diagram
The square root of 18 can be simplified to 3\(\sqrt{2}\). A diagram showing the factorization and simplification steps can provide a clear visual aid:
- Start with 18
- Prime factorization: 18 = 2 × 3 × 3
- Simplified form: \(3\sqrt{2}\)
4. Area Model
Consider a rectangle with one side of length \(\sqrt{18}\) and the other side 1 unit. This rectangle's area will be 18 square units, visually demonstrating how \(\sqrt{18}\) fits into geometric contexts.
These visualizations provide various perspectives on \(\sqrt{18}\), enhancing comprehension through different mathematical lenses.
Frequently Asked Questions about \(\sqrt{18}\)
Here are some common questions and answers about the square root of 18:
- What is the value of \(\sqrt{18}\)?
The value of \(\sqrt{18}\) is approximately 4.2426. In its simplest radical form, it is expressed as \(3\sqrt{2}\).
- Is 18 a perfect square?
No, 18 is not a perfect square because its square root is not an integer. The square root of 18 is an irrational number.
- Is the square root of 18 a rational or irrational number?
The square root of 18 is an irrational number because it cannot be expressed as a fraction of two integers and its decimal form is non-terminating and non-repeating.
- How is \(\sqrt{18}\) simplified?
The square root of 18 is simplified by expressing it as \(3\sqrt{2}\). This is done through prime factorization, where 18 is broken down into its prime factors: \(18 = 2 \times 3 \times 3\), and then \(\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}\).
- What is a perfect square number?
A perfect square number is an integer that is the square of another integer. For example, 25 is a perfect square because it is \(5^2\).
- Is the product of two perfect squares always a perfect square?
Yes, the product of two perfect squares is always a perfect square. For instance, \(25 \times 36 = 900\), which is a perfect square because \(\sqrt{900} = 30\).
- What is the side length of a square with an area of 18 square units?
The side length of a square with an area of 18 square units is \(\sqrt{18} = 3\sqrt{2}\), which is approximately 4.2426 units.
Tìm hiểu cách đơn giản hóa căn bậc hai của 18 (Sqrt(18)) trong video này. Chúng tôi hướng dẫn từng bước để hiểu và áp dụng các phương pháp hiệu quả nhất.
Cách Đơn Giản Hóa Căn Bậc Hai của 18: Sqrt(18)
READ MORE:
Khám phá cách tính và ý nghĩa của căn bậc hai của 18 (Sqrt(18)). Video này hướng dẫn chi tiết cách tính toán và ứng dụng căn bậc hai trong các tình huống thực tế.
Căn Bậc Hai của 18