Topic simplify 18 square root: Understanding how to simplify the square root of 18 is a fundamental skill in mathematics. This guide will walk you through the process step-by-step, making it easy to master. Whether you're a student or just looking to refresh your math skills, simplifying √18 will become a breeze with our clear and concise instructions.
Table of Content
- Simplifying the Square Root of 18
- Introduction to Square Roots
- Understanding Prime Factorization
- Steps to Simplify Square Roots
- Example: Simplifying the Square Root of 18
- Alternative Methods for Simplifying Square Roots
- Common Mistakes to Avoid
- Practical Applications of Simplifying Square Roots
- Conclusion
- YOUTUBE: Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai của 18. Video cung cấp các bước cụ thể và giải thích dễ hiểu.
Simplifying the Square Root of 18
The process of simplifying the square root of a number involves finding the prime factors of the number and then simplifying based on these factors. Here, we will simplify the square root of 18.
Step-by-Step Simplification
- First, factorize 18 into its prime factors:
\[ 18 = 2 \times 3^2 \]
- Rewrite the square root of 18 using these factors:
\[ \sqrt{18} = \sqrt{2 \times 3^2} \]
- Separate the factors inside the square root:
\[ \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} \]
- Simplify the square root of the perfect square \(3^2\):
\[ \sqrt{3^2} = 3 \]
- Combine the simplified factors:
\[ \sqrt{18} = \sqrt{2} \times 3 \]
Final Simplified Form
Thus, the simplified form of the square root of 18 is:
\[ \sqrt{18} = 3\sqrt{2} \]

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics, often encountered in various fields including algebra, geometry, and calculus. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because \( 4 \times 4 = 16 \).
Square roots are denoted by the radical symbol \( \sqrt{} \). The number under the radical symbol is called the radicand. For instance, in \( \sqrt{18} \), 18 is the radicand.
Properties of Square Roots
- Non-Negative Results: The principal square root of a non-negative number is always non-negative. For example, \( \sqrt{25} = 5 \), not -5.
- Perfect Squares: If the radicand is a perfect square (like 1, 4, 9, 16), its square root is an integer.
- Product Property: The square root of a product is equal to the product of the square roots of the factors. For example, \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \).
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots. For example, \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \), provided \( b \neq 0 \).
Why Simplify Square Roots?
Simplifying square roots makes it easier to work with them in equations and expressions. Simplified square roots are more manageable and often required for further mathematical operations. For instance, simplifying \( \sqrt{18} \) to \( 3\sqrt{2} \) helps in solving equations more efficiently.
Basic Steps to Simplify Square Roots
- Find the prime factorization of the radicand.
- Group the prime factors into pairs.
- Move one factor from each pair outside the radical symbol.
- Multiply the factors outside the radical.
- Keep any remaining factors inside the radical.
Using these steps, we can simplify square roots easily and accurately, making them an essential tool in our mathematical toolkit.
Understanding Prime Factorization
Prime factorization is the process of breaking down a composite number into its prime factors. Prime factors are prime numbers that multiply together to give the original number. This technique is crucial for simplifying square roots and solving various mathematical problems.
Steps to Find Prime Factorization
- Identify the Smallest Prime Factor: Start with the smallest prime number, which is 2. Check if the number is divisible by 2. If not, move to the next prime number (3, 5, 7, etc.).
- Divide and Repeat: Divide the number by the prime factor and write down the quotient. Continue the process with the quotient until it becomes 1. The divisors used are the prime factors.
- Verify the Factors: Multiply the prime factors together to ensure they equal the original number.
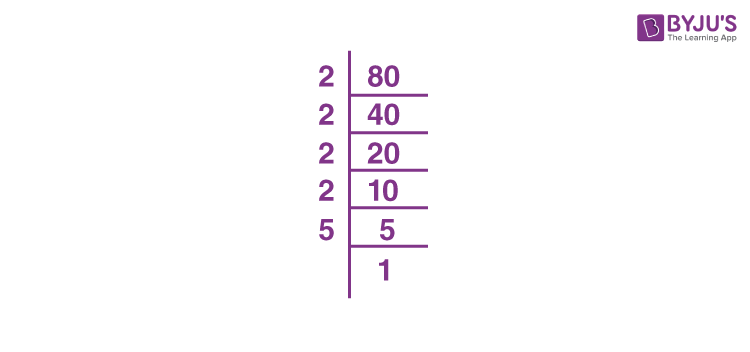
Example: Prime Factorization of 18
Let’s apply the steps to find the prime factorization of 18.
- 18 is an even number, so it is divisible by 2.
\[ 18 \div 2 = 9 \]
- Next, 9 is divisible by 3 (the next smallest prime number).
\[ 9 \div 3 = 3 \]
- Finally, 3 is a prime number.
\[ 3 \div 3 = 1 \]
Therefore, the prime factorization of 18 is:
\[ 18 = 2 \times 3 \times 3 = 2 \times 3^2 \]
Applications of Prime Factorization
- Simplifying Square Roots: Prime factorization helps in breaking down the radicand into smaller parts, making it easier to simplify square roots.
- Finding Least Common Multiples (LCM) and Greatest Common Divisors (GCD): Prime factors are used to calculate LCM and GCD of numbers.
- Solving Algebraic Equations: Prime factorization aids in solving equations involving polynomial expressions.
Understanding prime factorization is a foundational skill in mathematics, essential for simplifying complex problems and enhancing problem-solving abilities.
Steps to Simplify Square Roots
Simplifying square roots involves breaking down the radicand (the number inside the square root) into its prime factors and then simplifying the expression by removing perfect squares. Follow these detailed steps to simplify square roots efficiently:
Step-by-Step Process
- Find the Prime Factorization of the Radicand:
Break down the number under the square root into its prime factors. For example, the prime factorization of 18 is:
\[ 18 = 2 \times 3^2 \] - Rewrite the Square Root with Prime Factors:
Express the square root using the prime factors:
\[ \sqrt{18} = \sqrt{2 \times 3^2} \] - Separate the Perfect Squares:
Identify and separate the perfect square factors from the non-perfect square factors:
\[ \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} \] - Simplify the Square Root of Perfect Squares:
Simplify the square root of any perfect squares. In this case, \( \sqrt{3^2} = 3 \):
\[ \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3 \] - Combine the Simplified Terms:
Combine the simplified terms outside and inside the radical:
\[ 3 \times \sqrt{2} = 3\sqrt{2} \]
Thus, the simplified form of the square root of 18 is:
\[ \sqrt{18} = 3\sqrt{2} \]
Additional Tips
- Check for Further Simplification: Ensure that all factors inside the square root are in their simplest form and cannot be simplified further.
- Practice with Different Numbers: Apply these steps to various numbers to get comfortable with the process of simplifying square roots.
- Use Factor Trees: Creating a factor tree can help visualize the prime factorization process and simplify complex numbers.
By following these steps, you can simplify square roots with ease, making mathematical expressions more manageable and easier to work with in equations and problems.
Example: Simplifying the Square Root of 18
Let's go through the step-by-step process of simplifying the square root of 18. By following these detailed steps, you'll understand how to break down and simplify square roots effectively.
Step-by-Step Simplification
- Find the Prime Factorization of 18:
First, we need to break down 18 into its prime factors:
\[ 18 = 2 \times 3 \times 3 = 2 \times 3^2 \] - Rewrite the Square Root Using Prime Factors:
Express the square root of 18 using its prime factors:
\[ \sqrt{18} = \sqrt{2 \times 3^2} \] - Separate the Perfect Squares:
Identify and separate the perfect square factor (in this case, \(3^2\)) from the other factors:
\[ \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} \] - Simplify the Perfect Square:
Simplify the square root of the perfect square. Here, \( \sqrt{3^2} = 3 \):
\[ \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3 \] - Combine the Simplified Terms:
Multiply the simplified terms outside the radical sign:
\[ 3 \times \sqrt{2} = 3\sqrt{2} \]
Therefore, the simplified form of the square root of 18 is:
\[ \sqrt{18} = 3\sqrt{2} \]
Visualizing the Process
For a clearer understanding, here's a table summarizing the steps:
| Step | Description | Expression |
|---|---|---|
| 1 | Prime factorization of 18 | \[ 18 = 2 \times 3^2 \] |
| 2 | Rewrite using prime factors | \[ \sqrt{18} = \sqrt{2 \times 3^2} \] |
| 3 | Separate perfect squares | \[ \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} \] |
| 4 | Simplify perfect square | \[ \sqrt{3^2} = 3 \] |
| 5 | Combine terms | \[ 3 \times \sqrt{2} = 3\sqrt{2} \] |
By following these steps, you can simplify the square root of 18 and other similar expressions, making complex numbers more manageable and easier to work with in various mathematical contexts.
Alternative Methods for Simplifying Square Roots
While the prime factorization method is a common way to simplify square roots, there are alternative methods that can be used depending on the context and the complexity of the numbers involved. Here are a few alternative methods to consider:
Method 1: Estimation and Refinement
- Initial Estimation:
Estimate the square root by finding the two perfect squares it falls between. For example, \( \sqrt{18} \) is between \( \sqrt{16} = 4 \) and \( \sqrt{25} = 5 \).
- Refine the Estimate:
Use the average of the two numbers to refine your estimate. For instance, the average of 4 and 5 is 4.5. Check if 4.5 squared is close to 18. Continue refining as needed.
Method 2: Using Division and Average
- Choose an Initial Guess:
Start with a reasonable guess for the square root. For example, guess 4.5 for \( \sqrt{18} \).
- Calculate the Quotient:
Divide 18 by your guess:
\[ \frac{18}{4.5} = 4 \] - Find the Average:
Take the average of your guess and the quotient:
\[ \text{Average} = \frac{4.5 + 4}{2} = 4.25 \] - Iterate for Accuracy:
Repeat the process using 4.25 as the new guess, and continue iterating until you reach the desired level of accuracy.
Method 3: Simplifying Using Properties of Square Roots
- Recognize Multiples of Simplified Roots:
If the number is a multiple of a simpler square root, use this property. For example, \( \sqrt{72} \) can be simplified using \( \sqrt{36 \times 2} = 6\sqrt{2} \).
- Apply Simplification Rules:
Use the properties of square roots such as:
\[ \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \]
to simplify complex expressions.
Method 4: Graphical Methods
- Plotting on a Number Line:
Use a number line or graph to visually estimate and refine the square root. This method is useful for understanding the magnitude and approximation of square roots.
- Using Graphing Calculators:
Employ graphing calculators or software tools to visualize and calculate square roots accurately. This is particularly helpful for more complex or less intuitive numbers.
These alternative methods offer different approaches to simplifying square roots, catering to various preferences and contexts. By understanding and applying these methods, you can enhance your mathematical flexibility and problem-solving skills.
Common Mistakes to Avoid
When simplifying square roots, it's easy to make mistakes that can lead to incorrect results. Here are some common mistakes to avoid and tips on how to prevent them:
1. Incorrect Prime Factorization
One of the most frequent errors is making a mistake in the prime factorization of the radicand. Ensure that you correctly identify all prime factors:
- Break down the number into its smallest prime factors.
- Double-check your factorization by multiplying the factors back together to see if they equal the original number.
2. Misapplying Square Root Properties
Another common mistake is misapplying the properties of square roots. Remember these key properties:
- \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \)
- \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) (provided \( b \neq 0 \))
Ensure you apply these correctly and avoid combining or separating terms incorrectly.
3. Forgetting to Simplify Completely
Sometimes, students stop simplifying too early. Make sure to:
- Identify and extract all perfect squares from the radicand.
- Continue simplifying until no further simplification is possible.
4. Incorrectly Combining Like Terms
When simplifying expressions that include square roots, it’s essential to combine like terms correctly. For example:
- \( 2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3} \)
- Avoid trying to combine unlike terms, such as \( \sqrt{2} \) and \( \sqrt{3} \).
5. Neglecting the Plus-Minus Symbol
When taking the square root of a number in equations, remember to include both the positive and negative roots:
\( \sqrt{x^2} = \pm x \)
Neglecting the minus sign can lead to incomplete solutions in equations.
6. Rounding Too Early
In problems requiring exact answers, avoid rounding intermediate steps. Round only at the final step if necessary to maintain accuracy.
7. Using Decimal Approximations Incorrectly
While estimating square roots, ensure decimal approximations are used appropriately. For precise calculations, keep results in radical form when possible.
Tips to Avoid Mistakes
- Practice Regularly: Regular practice helps reinforce correct methods and reduces errors.
- Double-Check Work: Always review your steps and final answer to catch any mistakes.
- Understand Concepts: Deepen your understanding of underlying concepts rather than just memorizing procedures.
By being aware of these common mistakes and following these tips, you can improve your accuracy and efficiency in simplifying square roots.
Practical Applications of Simplifying Square Roots
Simplifying square roots is a fundamental skill in mathematics that has various practical applications. Understanding how to simplify square roots can make complex problems more manageable and is essential in different fields. Here are some practical applications:
1. Solving Quadratic Equations
- Quadratic Formula:
The quadratic formula often involves simplifying square roots. For example, solving \( ax^2 + bx + c = 0 \) using:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \] - Example:
Consider the quadratic equation \( x^2 - 6x + 9 = 0 \):
\[ x = \frac{6 \pm \sqrt{36 - 36}}{2} = \frac{6 \pm \sqrt{0}}{2} = 3 \]
2. Geometry and Trigonometry
- Calculating Distances:
The distance formula between two points \((x_1, y_1)\) and \((x_2, y_2)\) in a coordinate plane involves simplifying square roots:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \] - Example:
To find the distance between (1, 2) and (4, 6):
\[ d = \sqrt{(4 - 1)^2 + (6 - 2)^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \] - Trigonometric Functions:
Simplifying square roots is crucial in trigonometry when dealing with right triangles and the Pythagorean theorem:
\[ a^2 + b^2 = c^2 \]
3. Physics and Engineering
- Wave Equations:
In physics, wave equations often require simplification of square roots. For instance, the speed of a wave is given by:
\[ v = \sqrt{\frac{T}{\mu}} \]
where \( T \) is the tension and \( \mu \) is the mass per unit length. - Example:
If \( T = 100 \) N and \( \mu = 0.25 \) kg/m:
\[ v = \sqrt{\frac{100}{0.25}} = \sqrt{400} = 20 \text{ m/s} \]
4. Statistics and Probability
- Standard Deviation:
In statistics, the formula for standard deviation involves square roots. Simplifying these expressions helps in interpreting data more easily:
\[ \sigma = \sqrt{\frac{\sum (x_i - \mu)^2}{N}} \] - Example:
For a dataset {2, 4, 4, 4, 5, 5, 7, 9}, the variance is 4, so the standard deviation is:
\[ \sigma = \sqrt{4} = 2 \]
5. Simplifying Complex Numbers
- Magnitude of Complex Numbers:
Involving square roots, the magnitude of a complex number \( z = a + bi \) is found by:
\[ |z| = \sqrt{a^2 + b^2} \] - Example:
For \( z = 3 + 4i \):
\[ |z| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
These applications demonstrate the importance of simplifying square roots in various mathematical and real-world contexts. Mastering this skill can enhance problem-solving efficiency and accuracy across multiple disciplines.
Conclusion
Simplifying the square root of 18, or any square root, is a useful mathematical skill that can simplify further calculations and help in understanding the properties of numbers better. Let's summarize the steps and key takeaways from simplifying the square root of 18.
- Identify the prime factors of the number inside the square root. For 18, the prime factors are 2 and 3 (18 = 2 × 32).
- Rewrite the square root as the product of square roots: √18 = √(2 × 32).
- Separate the factors into distinct square roots: √(2 × 32) = √2 × √(32).
- Simplify the square root of the perfect square: √(32) = 3.
- Combine the simplified terms: √18 = 3√2.
The final simplified form of √18 is 3√2. This process not only simplifies the expression but also makes it easier to handle in further mathematical operations. Understanding how to simplify square roots can be applied to various areas such as algebra, geometry, and calculus.
Additionally, this method of simplification can be generalized to other numbers, enabling you to simplify square roots efficiently. Always remember to look for perfect square factors and use the properties of square roots to break down the expression into simpler forms.
In practical terms, simplifying square roots is useful in real-world applications such as engineering, physics, and any field that involves precise calculations. Whether you're calculating distances, areas, or working with equations, being able to simplify square roots quickly and accurately is a valuable skill.
Keep practicing with different numbers to reinforce your understanding and speed up the process. With consistent practice, you'll find that simplifying square roots becomes second nature.
Remember, the key steps are to factor the number, break it into simpler components, and simplify where possible. This approach not only makes the math easier but also helps in developing a deeper understanding of the properties of numbers.
Happy simplifying!
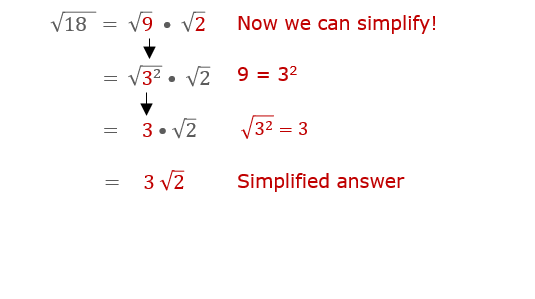
Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai của 18. Video cung cấp các bước cụ thể và giải thích dễ hiểu.
Cách Đơn Giản Hóa Căn Bậc Hai của 18: Sqrt(18)
READ MORE:
Video hướng dẫn chi tiết cách đơn giản hóa căn bậc hai của 18. Cung cấp các bước rõ ràng và dễ hiểu. Phù hợp cho các bạn học sinh và những ai yêu thích toán học.
Cách đơn giản hóa căn bậc hai của 18 #căn_bậc_hai #đơn_giản_hóa #toán_học #videongắn