Topic 18 square rooted: The concept of "18 square rooted" delves into the fascinating world of square roots, providing insights into its mathematical significance and practical applications. Discover how to simplify and approximate the square root of 18, explore various methods of calculation, and understand its relevance in everyday problems and advanced mathematical contexts.
Table of Content
- The Square Root of 18
- Introduction to Square Roots
- Understanding the Concept of Square Roots
- Definition and Basic Properties of Square Roots
- Mathematical Representation of Square Roots
- The Square Root of 18
- Simplifying Square Roots
- Prime Factorization Method
- Simplifying the Square Root of 18
- Decimal Approximation of the Square Root of 18
- Methods to Calculate Square Roots
- Manual Calculation Techniques
- Using a Calculator to Find Square Roots
- Visual Representation of the Square Root of 18
- Square Roots on the Number Line
- Applications of the Square Root of 18
- Square Roots in Geometry
- Square Roots in Algebra
- Square Roots in Real-World Problems
- YOUTUBE: Xem video này để học cách đơn giản hóa căn bậc hai của số 18. Nội dung bao gồm phương pháp tính toán và các ứng dụng thực tế của căn bậc hai trong bài viết với từ khóa '18 square rooted'.
The Square Root of 18
To find the square root of 18, we are looking for a number that, when multiplied by itself, equals 18. The square root of 18 can be represented as:
\[\sqrt{18}\]
This number is not a perfect square, which means its square root is an irrational number. We can simplify the square root of 18 by expressing it in terms of its prime factors:
\[18 = 2 \times 3^2\]
Using this factorization, we can simplify the square root:
\[\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3 = 3\sqrt{2}\]
Decimal Approximation
While the exact value of \(\sqrt{18}\) is \(3\sqrt{2}\), we can also provide a decimal approximation:
\[\sqrt{18} \approx 4.2426\]
This value is approximate and can be useful for practical calculations.
Visual Representation
The square root of 18 can be visualized on the number line as a point between 4 and 5:
- \(4^2 = 16\)
- \(5^2 = 25\)
Since \(18\) is closer to \(16\) than \(25\), \(\sqrt{18}\) is closer to \(4\) than \(5\), which aligns with our approximation of \(4.2426\).
Applications
Understanding the square root of 18 is useful in various fields such as engineering, physics, and mathematics. It can help in solving quadratic equations, understanding geometrical shapes, and analyzing natural phenomena.
In conclusion, the square root of 18 is \(3\sqrt{2}\), and its decimal approximation is approximately \(4.2426\). This value is crucial for both theoretical and practical applications in many areas of science and mathematics.

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because 3 × 3 = 9. This relationship is often represented using the radical symbol (√). Thus, the square root of 9 can be written as √9 = 3.
Square roots are not always whole numbers. When a number is not a perfect square, its square root is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal form is non-repeating and non-terminating. For instance, the square root of 18 is an irrational number.
To understand square roots better, let's break down the square root of 18:
- Radical Form: The square root of 18 is written as √18.
- Decimal Approximation: The square root of 18 is approximately 4.2426.
- Prime Factorization Method: By expressing 18 as a product of its prime factors (18 = 2 × 32), we can simplify the square root:
- √18 = √(2 × 32) = 3√2
The methods to calculate square roots include:
- Prime Factorization: Simplifies the square root by factoring the number into prime numbers.
- Long Division Method: A manual method to find more precise decimal values of square roots. For example, dividing 18 using this method gives a more accurate result of √18 ≈ 4.2426.
- Calculator: Modern calculators and software tools can quickly provide the square root of any number.
Understanding square roots is crucial as they appear frequently in various fields of science, engineering, and everyday calculations. They are used to solve quadratic equations, understand geometric properties, and in the calculation of areas and volumes.
Understanding the Concept of Square Roots
The concept of square roots is fundamental in mathematics and is denoted by the radical symbol (√). A square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). In other words, it is a number that, when multiplied by itself, gives the original number.
Square roots can be categorized into two types:
- Perfect Squares: Numbers like 1, 4, 9, 16, etc., are perfect squares because their square roots are integers (e.g., √4 = 2, √9 = 3).
- Non-Perfect Squares: Numbers like 2, 3, 5, 18, etc., are not perfect squares because their square roots are irrational numbers, which cannot be expressed as a simple fraction and have non-terminating, non-repeating decimal parts.
The square root of 18, for example, is denoted as √18. Since 18 is not a perfect square, √18 is an irrational number and can be simplified in its radical form or approximated in its decimal form. To simplify √18:
- Prime factorize 18: \( 18 = 2 \times 3^2 \).
- Express the square root using these factors: \( \sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2} \).
The simplified radical form is \( 3\sqrt{2} \). To express it in decimal form, we use the approximation of √2 (approximately 1.414), leading to:
\( 3 \times 1.414 = 4.242 \)
Thus, √18 ≈ 4.242 in decimal form.
Understanding the concept of square roots is crucial as it has numerous applications in geometry, algebra, and real-world problem-solving. For instance, finding the length of a side of a square given its area, solving quadratic equations, and determining distances in coordinate geometry all involve the use of square roots.
Definition and Basic Properties of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 18, denoted as \( \sqrt{18} \), is a number that when squared results in 18.
Basic Properties of Square Roots
- The square root of a positive number \( x \) is a number \( y \) such that \( y^2 = x \).
- Every positive number has two square roots: one positive (the principal square root) and one negative. For instance, \( \sqrt{18} = 3\sqrt{2} \) and \( -\sqrt{18} = -3\sqrt{2} \).
- The square root of 0 is 0.
- The square root of a negative number is not a real number. Instead, it is an imaginary number. For example, \( \sqrt{-18} = 3\sqrt{2}i \), where \( i \) is the imaginary unit.
- The square root function is the inverse of the squaring function.
Properties of Radicals
- \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \)
- \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)
- \( \sqrt{a^2} = |a| \)
Example: Square Root of 18
Let's consider the square root of 18. The prime factorization of 18 is:
18 = 2 \times 3^2
Applying the property of radicals, we get:
\(\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3 = 3\sqrt{2}\)
Therefore, the square root of 18 in simplest radical form is \( 3\sqrt{2} \). This value is approximately equal to 4.2426 when expressed as a decimal.
Special Characteristics
- \( \sqrt{18} \) is an irrational number because it cannot be expressed as a simple fraction. It is a non-repeating, non-terminating decimal.
- The square root symbol (√) is also known as the radical sign, and the number under the radical sign is called the radicand.
Mathematical Representation of Square Roots
Square roots are a fundamental concept in mathematics, representing a number that, when multiplied by itself, yields the original number. The square root of a number \( x \) is denoted as \( \sqrt{x} \). For example, the square root of 18 can be represented in various mathematical forms.
Here are some common representations:
- Radical Form: \( \sqrt{18} \)
- Exponent Form: \( 18^{1/2} \)
- Decimal Form: Approximately 4.2426
Using the prime factorization method, we can simplify \( \sqrt{18} \) as follows:
- Prime Factorization: \( 18 = 2 \times 3^2 \)
- Applying the square root: \[ \sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3 = 3\sqrt{2} \]
This shows that \( \sqrt{18} \) simplifies to \( 3\sqrt{2} \), which is an irrational number. In decimal form, this is approximately equal to 4.2426.
To find the square root of 18 using the long division method, follow these steps:
- Write 18 as 18.000000 to consider decimal places.
- Find a number which, when squared, is less than or equal to 18. Here, 4 × 4 = 16.
- Subtract 16 from 18 to get a remainder of 2. Bring down pairs of zeros.
- Continue the process, adding pairs of zeros, until you achieve the desired decimal accuracy.
Through this method, you will find that \( \sqrt{18} \approx 4.2426 \).
Understanding the different ways to represent and calculate square roots enhances your comprehension of this important mathematical concept, providing a strong foundation for further studies in algebra and geometry.

The Square Root of 18
The square root of 18, denoted as \(\sqrt{18}\), is a mathematical value that, when multiplied by itself, gives the original number 18. This can be expressed as:
\[
\sqrt{18} \times \sqrt{18} = 18
\]
Prime Factorization Method
To simplify the square root of 18, we can use the prime factorization method:
- First, factorize 18 into its prime factors: \(18 = 2 \times 3 \times 3\).
- Group the prime factors into pairs: \(18 = 2 \times 3^2\).
- Apply the square root to both sides: \(\sqrt{18} = \sqrt{2 \times 3^2}\).
- Simplify by taking the square root of the perfect square: \(\sqrt{18} = 3\sqrt{2}\).
Thus, the simplified form of the square root of 18 is \(3\sqrt{2}\).
Decimal Approximation
The square root of 18 can also be expressed in decimal form. Using a calculator or long division method, we find that:
\[
\sqrt{18} \approx 4.24264068712
\]
This value is approximate because the square root of 18 is an irrational number, meaning it cannot be exactly represented as a fraction or a finite decimal.
Properties of the Square Root of 18
- \(\sqrt{18}\) is an irrational number.
- The value in its simplest radical form is \(3\sqrt{2}\).
- In decimal form, \(\sqrt{18}\) is approximately 4.2426.
- \(\sqrt{18}\) is not a whole number since 18 is not a perfect square.
Visual Representation
On a number line, \(\sqrt{18}\) is positioned between 4 and 5 because \(4^2 = 16\) and \(5^2 = 25\). This helps us understand that:
\[
4 < \sqrt{18} < 5
\]
Conclusion
Understanding the square root of 18 involves recognizing it as an irrational number, simplifying it using prime factorization, and approximating its decimal value. These concepts are fundamental in various mathematical applications and provide a deeper insight into the nature of numbers.
Simplifying Square Roots
Simplifying square roots involves expressing the square root in its simplest form. This often means breaking down the radicand (the number under the square root sign) into its prime factors and simplifying any perfect squares.
Steps to Simplify Square Roots
- Identify the prime factors of the radicand.
- Group the prime factors into pairs of equal factors.
- Move one factor from each pair outside the square root.
- Multiply the factors outside the square root together.
- If any factors remain inside the square root, multiply them together.
Example: Simplifying the Square Root of 18
Let's simplify the square root of 18:
- Prime factorization of 18: \(18 = 2 \times 3 \times 3\)
- Group the prime factors: \(18 = 2 \times (3 \times 3)\)
- Since \(3 \times 3\) is a perfect square, we can take one 3 out of the square root:
- Rewrite the expression by removing the square of 3 from under the square root:
- The simplified form of \(\sqrt{18}\) is \(3 \sqrt{2}\).
\(\sqrt{18} = \sqrt{2 \times 3^2}\)
\(\sqrt{18} = 3 \sqrt{2}\)
Decimal Approximation
To find the decimal approximation of \(\sqrt{18}\), use the simplified form:
\(3 \sqrt{2} \approx 3 \times 1.414 \approx 4.242\)
Thus, \(\sqrt{18} \approx 4.242\) when rounded to three decimal places.
Using a Calculator
You can also use a calculator to find the square root of 18 directly:
- Enter 18.
- Press the square root (√) button.
- The calculator will display approximately 4.242640687.
Prime Factorization Method
The prime factorization method is a systematic approach to simplifying square roots by breaking down the number into its prime factors. This method helps in expressing the square root in its simplest form. Let's explore how this method works with an example, specifically simplifying the square root of 18.
- Identify Prime Factors:
Start by finding the prime factors of the number under the square root. Prime factors are the prime numbers that multiply together to give the original number. For 18, the prime factors are:
- 18 = 2 × 3 × 3
- Group the Prime Factors:
Next, group the prime factors in pairs. Since the square root of a product is the product of the square roots, you can simplify the square root by taking out pairs of the same number. For 18:
- √18 = √(2 × 3 × 3)
- Apply the Square Root:
Extract the square root of the pairs. In this case, the number 3 appears twice, so it can be taken out of the square root as a single 3:
- √(2 × 3 × 3) = 3√2
- Simplified Form:
After extracting the pairs, you are left with the simplest form of the square root. For 18, this is:
- √18 = 3√2
Using the prime factorization method not only simplifies the square root but also helps in understanding the factors that constitute the number. This method can be applied to any non-perfect square to express its square root in a simpler, more manageable form.
Here are a few more examples to illustrate the method:
- √45: Prime factors are 3, 3, and 5. Thus, √45 = √(3 × 3 × 5) = 3√5
- √72: Prime factors are 2, 2, 2, 3, and 3. Thus, √72 = √(2 × 2 × 2 × 3 × 3) = 6√2
- √50: Prime factors are 2 and 5, 5. Thus, √50 = √(2 × 5 × 5) = 5√2
The prime factorization method is a valuable tool for simplifying square roots and gaining a deeper understanding of the structure of numbers.
Simplifying the Square Root of 18
To simplify the square root of 18, we use the prime factorization method and the property of square roots that allows us to break down a square root of a product into the product of square roots.
First, find the prime factors of 18. The prime factorization of 18 is:
18 = 2 × 3 × 3
Group the prime factors into pairs where possible. In this case, we can pair the two 3's:
18 = 2 × (3 × 3)
Apply the property of square roots, which states that the square root of a product is equal to the product of the square roots:
\(\sqrt{18} = \sqrt{2 \times 3^2}\)
Simplify by taking the square root of the perfect square (3^2 = 9):
\(\sqrt{18} = \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3\)
Combine the terms to get the simplified form of the square root:
\(\sqrt{18} = 3\sqrt{2}\)
Thus, the simplified form of the square root of 18 is \(3\sqrt{2}\). This representation shows that the square root of 18 can be expressed as three times the square root of 2.
In decimal form, the square root of 18 is approximately 4.2426.

Decimal Approximation of the Square Root of 18
To simplify the square root of 18, we can use the method of prime factorization. Here’s a step-by-step guide:
- First, find the prime factors of 18:
- 18 can be broken down into 2 and 9.
- 9 can further be broken down into 3 and 3.
So, the prime factorization of 18 is \( 18 = 2 \times 3 \times 3 \) or \( 18 = 2 \times 3^2 \).
- Next, rewrite the square root of 18 using these prime factors:
\( \sqrt{18} = \sqrt{2 \times 3^2} \)
- Separate the square factors:
\( \sqrt{18} = \sqrt{2} \times \sqrt{3^2} \)
- Simplify by taking the square root of the perfect square (32):
\( \sqrt{3^2} = 3 \)
- Combine the simplified terms:
\( \sqrt{18} = 3 \times \sqrt{2} \)
Therefore, the simplified form of \( \sqrt{18} \) is \( 3\sqrt{2} \).
Methods to Calculate Square Roots
Calculating square roots can be approached using several methods, depending on the context and precision required:
- Estimation Method: Approximate the square root by identifying the nearest perfect squares.
- Prime Factorization Method: Decompose the number into its prime factors and simplify.
- Newton's Method: Iterative algorithm to approximate square roots.
- Using a Calculator: Directly compute using a scientific or graphing calculator.
- Binomial Expansion: For non-perfect squares, expand using binomial theorem.
Each method offers advantages based on the complexity of the number and the required accuracy.
Manual Calculation Techniques
Calculating the square root of 18 manually involves a few detailed steps:
- Estimate: Recognize that \( \sqrt{18} \) is between \( \sqrt{16} = 4 \) and \( \sqrt{25} = 5 \).
- First Approximation: Start with an initial guess, say \( 4.5 \).
- Iterative Calculation:
- Square the guess: \( 4.5^2 = 20.25 \).
- Adjust the guess based on whether the squared value is greater or less than 18.
- Refine the guess using the formula: \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{18}{x_n} \right) \).
- Convergence: Repeat steps until desired accuracy is achieved.
This method requires patience and arithmetic skills, but it's a valuable exercise in understanding square roots.
Using a Calculator to Find Square Roots
Calculating \( \sqrt{18} \) using a calculator is straightforward:
- Enter the Number: Turn on your calculator and input the number 18.
- Find the Square Root: Press the square root button (usually denoted as \( \sqrt{x} \) or \( x^{0.5} \)).
- Observe the Result: The calculator will display the approximate value of \( \sqrt{18} \).
- Accuracy: Depending on the calculator's precision, the result will be an approximation of the square root of 18.
This method is efficient for obtaining quick and accurate results.
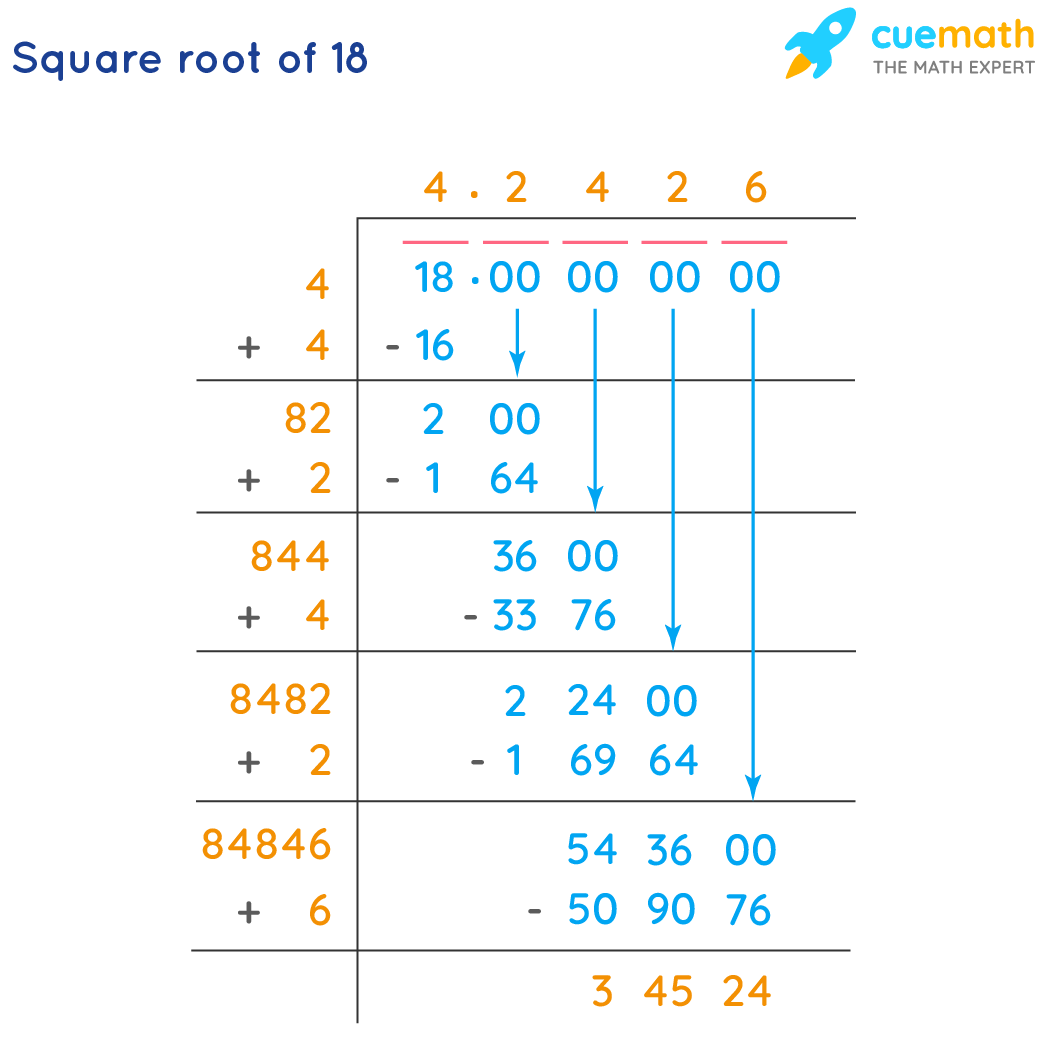
Visual Representation of the Square Root of 18
Visualizing \( \sqrt{18} \) can be done through various graphical representations:
- Number Line: Locate \( \sqrt{18} \) between 4 and 5 on a number line, illustrating its position relative to nearby integers.
- Geometric Interpretation: Imagine a square with an area of 18 square units. \( \sqrt{18} \) represents the length of each side of this square.
- Graphical Plot: Plot the function \( y = \sqrt{x} \) and observe where it intersects the vertical line at \( x = 18 \).
These visualizations help in understanding the magnitude and relationship of \( \sqrt{18} \) to other numbers.
Square Roots on the Number Line
The square root of 18, denoted as \( \sqrt{18} \), falls between 4 and 5 on the number line. To understand its exact placement, consider the following steps:
- Identify the perfect squares bracketing 18: \( 4^2 = 16 \) and \( 5^2 = 25 \).
- Since \( 16 < 18 < 25 \), \( \sqrt{18} \) is between 4 and 5.
- To narrow down further, estimate \( \sqrt{18} \) using averages or other approximation methods.
On a more detailed scale:
| Perfect Square | Value |
| \( 4^2 \) | 16 |
| \( 5^2 \) | 25 |
Therefore, \( \sqrt{18} \) can be visualized approximately here on the number line:

Applications of the Square Root of 18
The square root of 18, represented as \( \sqrt{18} \) or simplified to \( 3\sqrt{2} \), has numerous practical applications across various fields. Here are some key areas where it is utilized:
- Geometry: In geometry, the square root of 18 can be used to calculate the diagonal length of a square with sides of 9 units. This application helps in understanding distances and dimensions within geometric shapes.
- Physics: The concept of square roots appears in formulas that calculate distance, velocity, and acceleration, particularly under uniform acceleration conditions. For example, the distance covered by an object in free fall can be expressed using square roots.
- Engineering: In civil and mechanical engineering, the square root of 18 might be used in formulas to calculate stresses, forces, and other physical quantities. These calculations are crucial for designing safe and efficient structures.
- Statistics: Square roots are essential in the calculation of standard deviation, which measures the amount of variation or dispersion in a set of data. Understanding the square root of values helps in analyzing statistical data effectively.
- Computer Graphics: In computer graphics, square roots are used for calculating distances and angles between points in 3D space. The square root of 18 could be specifically applicable in certain algorithmic solutions or optimizations.
- Education: The square root of 18 serves as a teaching tool to help students grasp the concept of square roots, irrational numbers, and the relationship between different mathematical operations, enhancing their understanding of algebra and geometry.
- Financial Analysis: In finance, square roots are used in various calculations, such as assessing risk or deriving financial models. Although the square root of 18 might not be directly cited, the principles of extracting square roots are relevant in these contexts.
These examples illustrate the importance of the square root of 18 in both theoretical and practical applications, demonstrating its relevance across diverse fields and real-world scenarios.
Square Roots in Geometry
The concept of square roots is fundamental in geometry, especially when dealing with the dimensions and properties of shapes. The square root of 18, denoted as \( \sqrt{18} \), can be particularly useful in various geometric contexts.
Here are some detailed explanations and applications:
- Diagonal of a Square: The diagonal of a square can be found using the square root of the sum of the squares of its sides. For a square with side length \( s \), the diagonal \( d \) is given by \( d = s\sqrt{2} \). If the side length of a square is \( 3\sqrt{2} \), the diagonal will be \( 3\sqrt{2} \times \sqrt{2} = 3\sqrt{4} = 6 \). This shows that the square root of 18 (which is \( 3\sqrt{2} \)) can be used to find the diagonal of such squares.
- Right Triangles: In a right triangle, the Pythagorean theorem states that the square of the hypotenuse \( c \) is the sum of the squares of the other two sides \( a \) and \( b \). If one side of a right triangle is \( \sqrt{18} \) and another side is 3, then the hypotenuse \( c \) is given by:
- \( c^2 = (\sqrt{18})^2 + 3^2 \)
- \( c^2 = 18 + 9 \)
- \( c^2 = 27 \)
- \( c = \sqrt{27} = 3\sqrt{3} \)
- Circles and Sectors: The radius of a circle can be expressed using square roots. If the area of a circle is 18 square units, the radius \( r \) is found by rearranging the area formula \( A = \pi r^2 \) to \( r = \sqrt{\frac{A}{\pi}} = \sqrt{\frac{18}{\pi}} \).
- Equilateral Triangles: The height of an equilateral triangle with side length \( s \) is given by \( h = \frac{\sqrt{3}}{2}s \). If the side length is \( \sqrt{18} \), then the height is:
- \( h = \frac{\sqrt{3}}{2} \times \sqrt{18} \)
- \( h = \frac{\sqrt{3} \times \sqrt{18}}{2} = \frac{\sqrt{54}}{2} = \frac{3\sqrt{6}}{2} \)
- Volume and Surface Area of Solids: The square root of 18 can be used to find dimensions in 3D geometry. For example, the diagonal of a cube's face can be found using \( \sqrt{2} \) times the side length, and the space diagonal (corner to corner through the center) of the cube can be found using \( \sqrt{3} \) times the side length. If a side length of a cube is \( \sqrt{18} \), the space diagonal will be \( \sqrt{3} \times \sqrt{18} = \sqrt{54} \).
Understanding the square root of 18 and its applications in geometry helps in solving various geometric problems involving areas, volumes, and distances.

Square Roots in Algebra
The square root of 18 has various applications in algebra, often used to simplify expressions and solve equations. Understanding how to work with the square root of 18 can enhance problem-solving skills in algebraic contexts.
1. Simplifying Expressions
The square root of 18 can be simplified using prime factorization:
\(\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}\)
This simplified form is useful in algebraic expressions. For instance, in solving equations, the simplified form makes further calculations easier.
2. Solving Quadratic Equations
Square roots are crucial in solving quadratic equations. For example, consider the equation:
\(x^2 = 18\)
To solve for \(x\), take the square root of both sides:
\(x = \pm \sqrt{18} = \pm 3\sqrt{2}\)
Thus, the solutions to the equation are \(x = 3\sqrt{2}\) and \(x = -3\sqrt{2}\).
3. Radical Equations
Square roots appear in radical equations, where the variable is under a square root. Consider the equation:
\(\sqrt{2x + 6} = 3\)
To solve this, square both sides to eliminate the square root:
\(2x + 6 = 9\)
Then, solve for \(x\):
\(2x = 3 \implies x = \frac{3}{2}\)
4. Rationalizing the Denominator
In algebra, rationalizing the denominator involves eliminating radicals from the denominator of a fraction. For example:
\(\frac{1}{\sqrt{18}} = \frac{1}{3\sqrt{2}}\)
To rationalize, multiply the numerator and the denominator by \(\sqrt{2}\):
\(\frac{1}{3\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{6}\)
5. Exponential Form
The square root of 18 can also be expressed in exponential form, which is useful in various algebraic manipulations:
\(\sqrt{18} = 18^{\frac{1}{2}}\)
This form is particularly helpful when applying the properties of exponents in algebra.
6. Real and Complex Solutions
When dealing with negative numbers under the square root, the solutions become complex. For example:
\(\sqrt{-18} = 3\sqrt{2}i\)
This extends the understanding of algebra to include complex numbers, enhancing problem-solving capabilities.
Square Roots in Real-World Problems
Square roots play a significant role in solving various real-world problems across different fields. Below are some practical applications:
1. Engineering and Construction
In engineering and construction, square roots are used to calculate distances, areas, and other measurements. For instance, the Pythagorean Theorem, which includes square roots, helps determine the length of the diagonal in a right-angled triangle.
- Using the Pythagorean Theorem: \(a^2 + b^2 = c^2\)
- Example: To find the length of the diagonal (hypotenuse) in a right triangle where the other two sides are 9 and 12 units: \[ c = \sqrt{9^2 + 12^2} = \sqrt{81 + 144} = \sqrt{225} = 15 \]
2. Architecture and Design
Architects often use square roots to calculate slopes, areas, and other critical dimensions. This ensures structures are both aesthetically pleasing and structurally sound.
3. Finance and Economics
Square roots are used in financial formulas to calculate compound interest, volatility in stock prices, and more. For example:
- Compound Interest Formula: \(A = P \left(1 + \frac{r}{n}\right)^{nt}\)
- Volatility: Square roots are used to annualize the volatility of daily stock returns: \[ \sigma_{\text{annual}} = \sigma_{\text{daily}} \times \sqrt{250} \]
4. Physics
In physics, square roots appear in various fundamental equations, including those related to motion, energy, and waves.
- Example: The formula for the period of a pendulum: \[ T = 2\pi \sqrt{\frac{L}{g}} \] where \(T\) is the period, \(L\) is the length of the pendulum, and \(g\) is the acceleration due to gravity.
5. Computer Graphics and Game Development
Square roots are crucial in computer graphics to compute distances between points, normalize vectors, and handle transformations.
- Distance Formula in 2D: \[ D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
6. Medicine and Biology
Square roots are used in medical imaging, pharmacokinetics, and biology for various calculations, such as determining the body surface area or analyzing the growth rate of populations.
7. Sports and Athletics
Square roots help in analyzing trajectories, optimizing performance, and understanding statistical variations in sports.
These applications highlight the importance of understanding square roots and their practical uses in solving real-world problems effectively.
Xem video này để học cách đơn giản hóa căn bậc hai của số 18. Nội dung bao gồm phương pháp tính toán và các ứng dụng thực tế của căn bậc hai trong bài viết với từ khóa '18 square rooted'.
Video hướng dẫn cách đơn giản hóa căn bậc hai của 18: Sqrt(18)
READ MORE:
Giá trị căn bậc hai của 50 cộng với căn bậc hai của 18 là một bài toán toán học thú vị. Xem video này để hiểu rõ hơn về cách tính và ứng dụng của hai căn bậc hai này.
Căn bậc hai của 50 + căn bậc hai của 18 | MathTutorial.com