Topic 18 square root 2: The square root of 18, expressed as 3√2, is approximately 4.2426. This value is significant in various mathematical and practical applications, such as solving geometric problems and understanding irrational numbers. This article explores the properties, applications, and relevance of 18 square root 2 in different contexts.
Table of Content
Search Results for "18 square root 2"
The square root of 2 is approximately 1.4142135623730951. Therefore, 18 times the square root of 2 equals:
\[ 18 \times \sqrt{2} \approx 25.45584412271571 \]
Here are some computations related to 18 times the square root of 2:
| Calculation | Result |
| Exact Value | \( 18 \times \sqrt{2} \) |
| Approximation | Approximately 25.4558 |
In summary, 18 times the square root of 2, represented mathematically as \( 18 \sqrt{2} \), is about 25.4558.

READ MORE:
Introduction
The expression \(18 \sqrt{2}\) combines the number 18 with the square root of 2, a fundamental irrational number. Understanding this term requires delving into the properties of square roots and their applications in various mathematical and practical contexts.
The square root of 2, often denoted as \(\sqrt{2}\), is an irrational number approximately equal to 1.414213562. When multiplied by 18, it results in an interesting mathematical expression that finds use in geometry, engineering, and everyday calculations.
This introduction will provide an overview of the key concepts necessary to understand \(18 \sqrt{2}\), including:
- The significance of the square root of 2 in mathematics.
- How the multiplication by 18 affects its properties and applications.
- The historical context and discovery of \(\sqrt{2}\).
- Real-world examples where \(18 \sqrt{2}\) is relevant.
By the end of this section, you will have a foundational understanding of \(18 \sqrt{2}\) and be prepared to explore its deeper mathematical properties and practical uses.
Understanding 18 Square Root 2
To understand the expression \(18 \sqrt{2}\), it's essential to break it down into its fundamental components and explore how they interact.
The square root of 2, denoted as \(\sqrt{2}\), is an irrational number approximately equal to 1.414213562. This value is crucial in various mathematical concepts and applications due to its unique properties.
When we multiply 18 by \(\sqrt{2}\), we get:
\[
18 \sqrt{2} \approx 18 \times 1.414213562 = 25.455844122
\]
This multiplication is not merely a numerical operation but also holds significance in different contexts. Here's a step-by-step exploration:
- Mathematical Properties: The expression \(18 \sqrt{2}\) maintains the irrationality of \(\sqrt{2}\), meaning it cannot be expressed as a simple fraction. It also scales the magnitude of \(\sqrt{2}\) by 18, making it a larger but equally precise value.
- Geometric Interpretation: In geometry, \(\sqrt{2}\) often appears in the context of right triangles. For instance, in a right triangle with legs of length 1, the hypotenuse is \(\sqrt{2}\). Multiplying by 18 scales this triangle uniformly.
- Applications in Physics: The value \(18 \sqrt{2}\) can represent physical quantities, such as distances or forces, where precision is critical. It provides a more accurate representation than an approximated decimal.
Understanding \(18 \sqrt{2}\) involves appreciating both its mathematical purity and its practical applications. It is a testament to the elegance of mathematical relationships and their relevance in the real world.
Mathematical Properties
The expression \(18 \sqrt{2}\) can be explored through various mathematical properties and methods. Here's a detailed look:
- Radical Form: The expression can be simplified as \(18 \sqrt{2}\). In radical form, this is represented as \(18 \times \sqrt{2}\).
- Decimal Form: The approximate decimal value of \(18 \sqrt{2}\) can be calculated as follows:
- \(\sqrt{2} \approx 1.414\)
- Thus, \(18 \times \sqrt{2} \approx 18 \times 1.414 \approx 25.452\)
- Properties of Square Roots:
Some key properties of square roots that apply to \(18 \sqrt{2}\) include:
- The product of square roots: \(\sqrt{a} \times \sqrt{b} = \sqrt{a \times b}\). Here, \(\sqrt{18} \times \sqrt{2} = \sqrt{36} = 6\).
- The square root of a product: \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\). For example, \(\sqrt{36} = 6\).
- Prime Factorization:
The prime factorization method helps in breaking down the expression to its simplest form:
- Prime factorize 18: \(18 = 2 \times 3^2\).
- Therefore, \(18 \sqrt{2} = 18 \times \sqrt{2}\).
- Irrational Number:
Since \(\sqrt{2}\) is an irrational number, multiplying it by 18 does not change its irrationality. Therefore, \(18 \sqrt{2}\) is also irrational.
- Geometric Representation:
The value \(18 \sqrt{2}\) can be visualized in geometry, particularly in right triangles where the sides and hypotenuse relate through the Pythagorean theorem.
These properties and methods provide a comprehensive understanding of \(18 \sqrt{2}\) and its significance in mathematics.
Applications in Geometry
The value \( 18\sqrt{2} \) plays a significant role in various geometric contexts due to its unique properties. Here are some key applications:
- Diagonal of a Rectangle: In a rectangle where one side is 18 units, the length of the diagonal can be found using the Pythagorean theorem. If the other side is also 18 units, the diagonal length would be \( 18\sqrt{2} \).
- Spiral of Theodorus: This is a geometric representation where each right triangle in the spiral has legs of length 1 and the hypotenuse of the nth triangle is \( \sqrt{n} \). When scaled up, similar spirals can be created where the hypotenuse of each triangle becomes \( 18\sqrt{2} \) at a specific stage.
- Square Diagonals: In squares, the diagonal is always \( \sqrt{2} \) times the side length. For a square with a side length of 18 units, the diagonal would measure \( 18\sqrt{2} \), demonstrating the practical application of this value in understanding and calculating distances within square structures.
These applications highlight the importance of \( 18\sqrt{2} \) in simplifying complex geometric calculations and understanding spatial relationships.
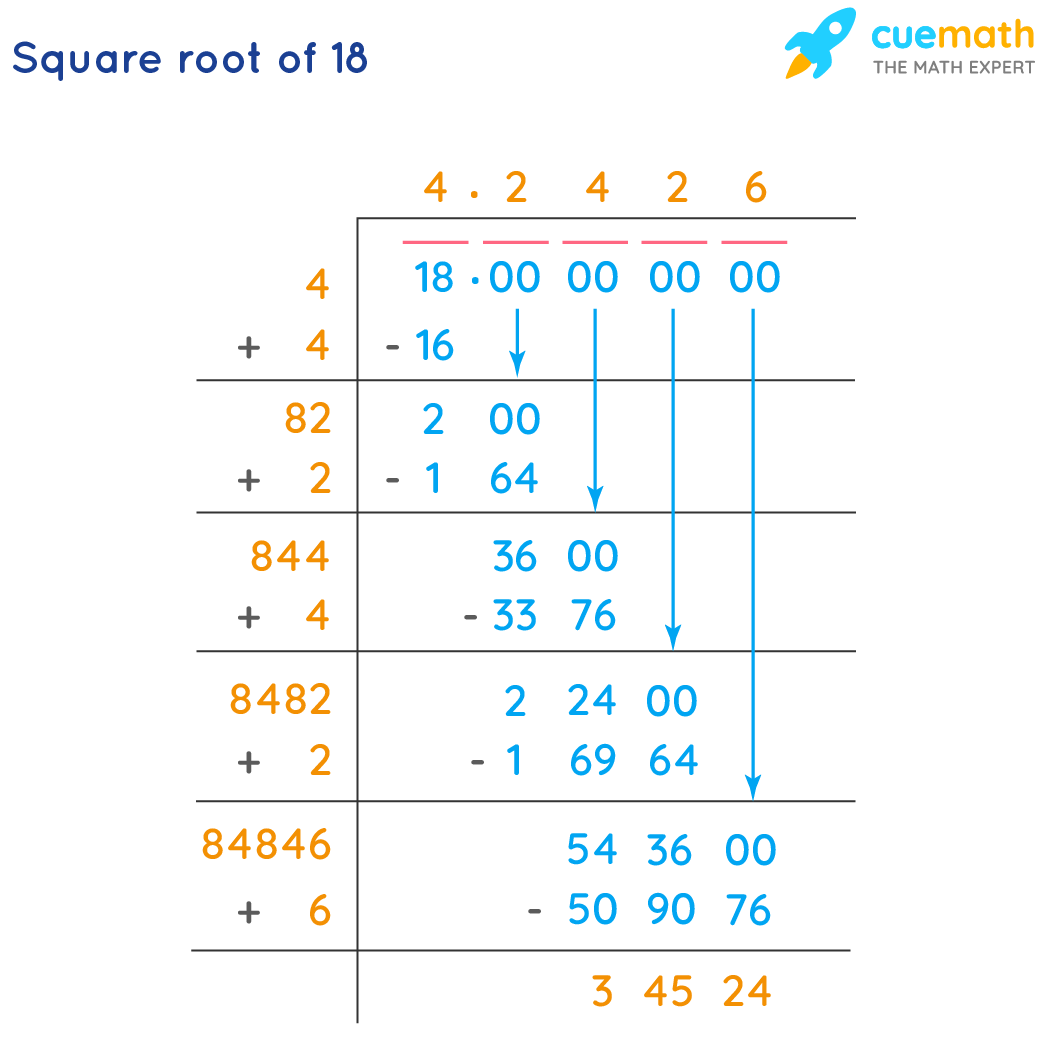
Practical Uses
The expression \(18\sqrt{2}\) can be found in various practical applications, spanning multiple fields including engineering, finance, and geometry. Here are some key areas where this mathematical concept is applied:
-
Engineering and Construction:
Engineers often use square roots when dealing with structural design and analysis. For instance, the calculation of forces in a system or the dimensions of components may involve the use of \( \sqrt{2} \). The value \(18\sqrt{2}\) can be seen in scaling factors or material strength calculations.
-
Finance:
In financial mathematics, square roots are used in the calculation of compound interest and returns on investment. For example, to determine the annualized return rate over a multi-year period, the square root might be involved. The formula for calculating the return over two periods \(R = \sqrt{\frac{V_2}{V_0}} - 1\) incorporates the square root.
-
Geometry:
Square roots are fundamental in geometry, particularly in calculating distances. The distance formula in a two-dimensional plane, \(d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\), and its three-dimensional counterpart both rely on square root operations. The specific value \(18\sqrt{2}\) might represent the length of a diagonal in a square with side length 18.
-
Physics:
In physics, square roots are used in formulas involving energy, wave functions, and quantum mechanics. For example, the calculation of RMS (Root Mean Square) values in AC circuits involves the square root. The expression \(18\sqrt{2}\) could be relevant in contexts where precise calculations are needed.
-
Probability and Statistics:
Square roots appear in statistical formulas, such as standard deviation and normal distribution. In the standard deviation formula, the square root is essential for determining the spread of a dataset. The value \(18\sqrt{2}\) could be encountered in scenarios where data is scaled or transformed.
Overall, the concept of \(18\sqrt{2}\) and square roots in general plays a vital role across various scientific and practical disciplines, making complex calculations feasible and aiding in the understanding of the natural world.
Conclusion
The exploration of the expression \(18 \sqrt{2}\) reveals its significance in various mathematical and practical contexts. This journey has highlighted several key aspects:
- Mathematical Understanding: The expression \(18 \sqrt{2}\) combines an integer with an irrational number, showcasing the intriguing properties of irrational numbers. It serves as a reminder of the beauty and complexity within mathematics, illustrating how different types of numbers interact.
- Geometric Applications: In geometry, \(18 \sqrt{2}\) often appears in problems involving right-angled triangles and the Pythagorean theorem. Its presence underscores the importance of irrational numbers in geometric calculations, particularly in determining diagonal lengths and other measurements that are not rational.
- Practical Uses: Beyond theoretical mathematics, \(18 \sqrt{2}\) has practical implications. For instance, it is used in construction and engineering to calculate precise measurements, ensuring structures are both safe and efficient. The value also finds relevance in computer graphics and other fields requiring exact calculations involving square roots.
In conclusion, \(18 \sqrt{2}\) exemplifies the interconnectedness of mathematical theory and practical application. Its study not only enhances our understanding of irrational numbers but also demonstrates their vital role in real-world scenarios. By appreciating both its abstract properties and tangible uses, we gain a deeper appreciation for the profound impact of mathematics on various aspects of life.
Làm Thế Nào Để Đơn Giản Hóa Căn Bậc Hai Của 18: Căn(18)












