Topic square root of 18 simplified: Understanding the square root of 18 and its simplification is essential for mastering various mathematical concepts. In this guide, we'll explore simple and effective methods to simplify the square root of 18, making it easier to handle in calculations and applications. Dive in to enhance your mathematical skills with our comprehensive and easy-to-follow steps.
Table of Content
- Simplifying the Square Root of 18
- Introduction to Square Roots
- What is the Square Root of 18?
- Understanding Square Root Simplification
- Methods to Simplify the Square Root of 18
- Prime Factorization Method
- Step-by-Step Simplification Process
- Mathematical Explanation
- Examples of Simplifying Square Roots
- Why Simplify Square Roots?
- Applications of Simplified Square Roots
- Common Mistakes to Avoid
- Practice Problems
- Advanced Simplification Techniques
- Additional Resources
- YOUTUBE: Hướng dẫn cách đơn giản hóa căn bậc hai của 18 một cách chi tiết và dễ hiểu. Khám phá cách làm thế nào để tính căn bậc hai của số 18 một cách nhanh chóng.
Simplifying the Square Root of 18
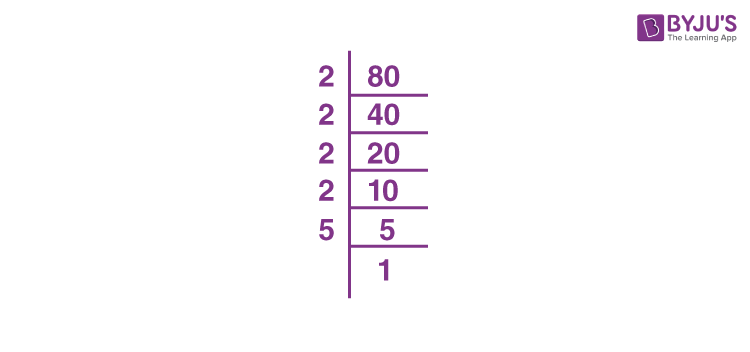
The process of simplifying the square root of 18 involves finding the prime factors of 18 and simplifying them under the radical sign.
Step-by-Step Simplification
- Find the prime factors of 18:
- 18 can be factored into 2 and 9.
- 9 can be further factored into 3 and 3.
- So, the prime factors of 18 are 2, 3, and 3.
- Express 18 as the product of its prime factors:
18 = 2 × 32
- Rewrite the square root of 18 using these prime factors:
\(\sqrt{18} = \sqrt{2 \times 3^2}\)
- Separate the square root into two parts:
\(\sqrt{18} = \sqrt{2} \times \sqrt{3^2}\)
- Simplify the square root of the perfect square:
\(\sqrt{3^2} = 3\)
- Combine the simplified parts:
\(\sqrt{18} = 3\sqrt{2}\)
Conclusion
Thus, the simplified form of the square root of 18 is \(3\sqrt{2}\).

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics, providing the basis for various advanced topics. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because \(3 \times 3 = 9\).
Square roots are denoted by the radical symbol (√). For any positive number \( x \), the square root is written as \( \sqrt{x} \). Understanding how to simplify square roots, like \( \sqrt{18} \), is crucial for simplifying mathematical expressions and solving equations.
Let's break down the process step-by-step:
-
Identify Perfect Squares: The first step in simplifying a square root is to identify any perfect square factors. A perfect square is a number that can be expressed as the product of an integer with itself (e.g., 1, 4, 9, 16).
-
Factor the Number: Decompose the number under the square root into its prime factors. For 18, the prime factorization is:
\[
18 = 2 \times 3^2
\] -
Separate the Perfect Squares: Rewrite the square root by separating the perfect square factors from the non-perfect square factors:
\[
\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}
\] -
Simplify: Simplify the expression by taking the square root of the perfect square:
\[
\sqrt{18} = \sqrt{2} \times 3 = 3\sqrt{2}
\]
By following these steps, we have simplified \( \sqrt{18} \) to \( 3\sqrt{2} \). This method can be applied to simplify other square roots, making calculations more manageable and expressions more concise.
What is the Square Root of 18?
The square root of 18 is a value that, when multiplied by itself, equals 18. This can be expressed as:
\[
\sqrt{18} \approx 4.242640687
\]
However, the square root of 18 can be simplified to make it more manageable for calculations and applications. To understand the simplification process, let's break it down step-by-step:
-
Prime Factorization: Begin by finding the prime factors of 18. The prime factorization of 18 is:
\[
18 = 2 \times 3 \times 3 = 2 \times 3^2
\] -
Rewrite the Square Root: Express the square root of 18 using its prime factors:
\[
\sqrt{18} = \sqrt{2 \times 3^2}
\] -
Separate the Perfect Square: Identify and separate the perfect square (which is \( 3^2 \) in this case) from the non-perfect square:
\[
\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}
\] -
Simplify: Simplify the expression by taking the square root of the perfect square:
\[
\sqrt{18} = \sqrt{2} \times 3 = 3\sqrt{2}
\]
Thus, the simplified form of \( \sqrt{18} \) is \( 3\sqrt{2} \). This simplified form is easier to work with in mathematical equations and applications, providing a clearer understanding of the square root of 18.
Understanding Square Root Simplification
Simplifying square roots is a fundamental skill in mathematics that makes complex calculations more manageable. The goal is to express a square root in its simplest form by breaking it down into its prime factors and identifying perfect squares. Let's explore the process of simplification step-by-step:
-
Identify the Number: Start with the number under the square root. For example, let's simplify \( \sqrt{18} \).
-
Prime Factorization: Find the prime factors of the number. Prime factorization is the process of breaking down a number into its prime factors. For 18, the prime factorization is:
\[
18 = 2 \times 3 \times 3 = 2 \times 3^2
\] -
Rewrite the Square Root: Express the square root using the prime factors:
\[
\sqrt{18} = \sqrt{2 \times 3^2}
\] -
Separate the Perfect Squares: Identify and separate the perfect squares from the non-perfect squares within the square root:
\[
\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}
\] -
Simplify the Expression: Simplify the expression by taking the square root of the perfect square:
\[
\sqrt{3^2} = 3
\]So,
\[
\sqrt{18} = \sqrt{2} \times 3 = 3\sqrt{2}
\] -
Result: The simplified form of \( \sqrt{18} \) is \( 3\sqrt{2} \). This form is easier to work with in various mathematical contexts, such as solving equations or performing arithmetic operations.
Understanding and applying these steps to simplify square roots will enhance your ability to solve mathematical problems efficiently and accurately.
Methods to Simplify the Square Root of 18
Simplifying the square root of 18 can be achieved through various methods. The goal is to express \( \sqrt{18} \) in its simplest form. Here are the most common methods to simplify \( \sqrt{18} \):
-
Prime Factorization Method:
-
Find the prime factors of 18. The prime factorization of 18 is:
\[
18 = 2 \times 3^2
\] -
Rewrite the square root using the prime factors:
\[
\sqrt{18} = \sqrt{2 \times 3^2}
\] -
Separate the perfect square factor from the non-perfect square factor:
\[
\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}
\] -
Simplify by taking the square root of the perfect square:
\[
\sqrt{3^2} = 3
\]So,
\[
\sqrt{18} = \sqrt{2} \times 3 = 3\sqrt{2}
\]
-
-
Estimation Method:
-
Estimate the square root by finding two perfect squares between which 18 lies. For example, 16 and 25:
\[
4^2 = 16 \quad \text{and} \quad 5^2 = 25
\] -
Since 18 is closer to 16, start with 4.5 and adjust as necessary. Refine the estimate using averages and closer approximations:
\[
\sqrt{18} \approx 4.242
\]
-
-
Using a Calculator:
-
Simply use a calculator to find the decimal approximation:
\[
\sqrt{18} \approx 4.242640687
\]
-
Among these methods, the prime factorization method provides the exact simplified form \( 3\sqrt{2} \), which is often more useful for algebraic manipulations and theoretical work.
Prime Factorization Method
The prime factorization method is an effective way to simplify square roots by breaking down the number into its prime factors and simplifying any perfect squares. Let's go through this method step-by-step to simplify \( \sqrt{18} \):
-
Find the Prime Factors: Begin by determining the prime factors of 18. Prime factorization involves breaking down 18 into the product of prime numbers:
\[
18 = 2 \times 3 \times 3 = 2 \times 3^2
\] -
Express the Square Root: Rewrite the square root of 18 using its prime factors:
\[
\sqrt{18} = \sqrt{2 \times 3^2}
\] -
Separate the Perfect Square: Identify and separate the perfect square factor from the non-perfect square factor:
\[
\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}
\] -
Simplify the Expression: Simplify by taking the square root of the perfect square:
\[
\sqrt{3^2} = 3
\]Thus,
\[
\sqrt{18} = \sqrt{2} \times 3 = 3\sqrt{2}
\]
By following these steps, we have simplified \( \sqrt{18} \) to \( 3\sqrt{2} \). This simplified form is easier to work with in mathematical equations and provides a clearer understanding of the value.
Step-by-Step Simplification Process
Simplifying the square root of 18 involves a systematic approach to break down the number into its prime factors and simplify the square root expression. Follow these detailed steps to simplify \( \sqrt{18} \):
-
Find the Prime Factors of 18: The first step is to determine the prime factors of 18. This involves breaking down 18 into the product of prime numbers:
\[
18 = 2 \times 3 \times 3 = 2 \times 3^2
\] -
Rewrite the Square Root Using Prime Factors: Express the square root of 18 using its prime factors:
\[
\sqrt{18} = \sqrt{2 \times 3^2}
\] -
Separate the Perfect Square Factor: Identify the perfect square factor within the square root. In this case, \( 3^2 \) is the perfect square:
\[
\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}
\] -
Simplify the Perfect Square: Take the square root of the perfect square factor, which is \( 3^2 \):
\[
\sqrt{3^2} = 3
\] -
Combine the Simplified Terms: Multiply the simplified perfect square factor by the remaining square root term:
\[
\sqrt{18} = \sqrt{2} \times 3 = 3\sqrt{2}
\]
By following these steps, we have successfully simplified \( \sqrt{18} \) to \( 3\sqrt{2} \). This simplified form is more manageable and easier to use in mathematical equations and problem-solving.
Mathematical Explanation
The process of simplifying the square root of 18 involves understanding the properties of square roots and the factorization of numbers. Here's a detailed mathematical explanation of how to simplify \( \sqrt{18} \):
-
Understanding Square Roots: The square root of a number \( x \), denoted as \( \sqrt{x} \), is a value that, when multiplied by itself, equals \( x \). For instance, \( \sqrt{9} = 3 \) because \( 3 \times 3 = 9 \).
-
Prime Factorization: Begin by breaking down the number 18 into its prime factors. Prime factorization involves expressing a number as the product of its prime numbers:
\[
18 = 2 \times 3 \times 3 = 2 \times 3^2
\]Here, 2 and 3 are prime numbers, and 3 is squared.
-
Expressing the Square Root: Use the prime factorization to rewrite the square root of 18:
\[
\sqrt{18} = \sqrt{2 \times 3^2}
\] -
Separating the Factors: Separate the perfect square factor from the non-perfect square factor. A perfect square is a number that has an integer as its square root:
\[
\sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}
\] -
Simplifying the Perfect Square: Simplify the square root of the perfect square. In this case, \( \sqrt{3^2} = 3 \):
\[
\sqrt{3^2} = 3
\] -
Combining the Results: Multiply the simplified square root of the perfect square by the remaining square root term:
\[
\sqrt{18} = \sqrt{2} \times 3 = 3\sqrt{2}
\]
Therefore, the simplified form of \( \sqrt{18} \) is \( 3\sqrt{2} \). This approach uses the properties of square roots and prime factorization to simplify the expression, making it easier to work with in various mathematical contexts.
Examples of Simplifying Square Roots
Simplifying square roots involves breaking down the number under the square root into its prime factors and simplifying any perfect squares. Here are some detailed examples to illustrate the process:
-
Simplifying \( \sqrt{18} \):
- Find the prime factors of 18:
\[
18 = 2 \times 3^2
\] - Rewrite the square root using these prime factors:
\[
\sqrt{18} = \sqrt{2 \times 3^2}
\] - Separate the perfect square factor:
\[
\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}
\] - Simplify the perfect square:
\[
\sqrt{3^2} = 3
\] - Combine the simplified terms:
\[
\sqrt{18} = 3\sqrt{2}
\]
- Find the prime factors of 18:
-
Simplifying \( \sqrt{50} \):
- Find the prime factors of 50:
\[
50 = 2 \times 5^2
\] - Rewrite the square root using these prime factors:
\[
\sqrt{50} = \sqrt{2 \times 5^2}
\] - Separate the perfect square factor:
\[
\sqrt{50} = \sqrt{2 \times 5^2} = \sqrt{2} \times \sqrt{5^2}
\] - Simplify the perfect square:
\[
\sqrt{5^2} = 5
\] - Combine the simplified terms:
\[
\sqrt{50} = 5\sqrt{2}
\]
- Find the prime factors of 50:
-
Simplifying \( \sqrt{72} \):
- Find the prime factors of 72:
\[
72 = 2^3 \times 3^2
\] - Rewrite the square root using these prime factors:
\[
\sqrt{72} = \sqrt{2^3 \times 3^2}
\] - Separate the perfect square factors:
\[
\sqrt{72} = \sqrt{2^3 \times 3^2} = \sqrt{2^2 \times 2 \times 3^2} = \sqrt{2^2} \times \sqrt{2} \times \sqrt{3^2}
\] - Simplify the perfect squares:
\[
\sqrt{2^2} = 2 \quad \text{and} \quad \sqrt{3^2} = 3
\] - Combine the simplified terms:
\[
\sqrt{72} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}
\]
- Find the prime factors of 72:
These examples show how to simplify square roots by breaking down the number into its prime factors and simplifying any perfect squares. This method provides a clear and manageable way to work with square roots in mathematical problems.

Why Simplify Square Roots?
Simplifying square roots is a fundamental skill in mathematics that offers several benefits. Below are the primary reasons for simplifying square roots:
- Easier Interpretation: Simplified square roots are often easier to understand and interpret, especially when working with large numbers or complex expressions.
- Simplified Computations: Working with simplified square roots can make arithmetic operations such as addition, subtraction, multiplication, and division more straightforward. For example, it's easier to add or subtract roots when they are in their simplest form.
- Exact Values: Simplified square roots provide exact values rather than decimal approximations. This is crucial in fields requiring precision, such as engineering and physics.
- Identifying Patterns: Simplifying square roots can help in recognizing patterns and relationships between numbers. This can be particularly useful in algebra and higher-level mathematics.
- Improved Problem Solving: Many mathematical problems, especially those involving quadratic equations and geometry, require simplified square roots for accurate solutions.
- Aesthetic Appeal: Simplified expressions often look cleaner and more elegant, which can make your work more presentable and easier to follow.
Below is a step-by-step example demonstrating the simplification of the square root of 18:
- Find the prime factorization of 18: \(18 = 2 \times 3^2\).
- Express the square root using the prime factors: \(\sqrt{18} = \sqrt{2 \times 3^2}\).
- Separate the factors under the square root: \(\sqrt{18} = \sqrt{2} \times \sqrt{3^2}\).
- Simplify the square of 3: \(\sqrt{3^2} = 3\).
- Combine the simplified parts: \(\sqrt{18} = 3\sqrt{2}\).
Thus, the simplified form of \(\sqrt{18}\) is \(3\sqrt{2}\).
By following these steps, you can simplify square roots and enjoy the benefits outlined above.
Applications of Simplified Square Roots
The simplification of square roots has numerous practical applications in various fields of science, engineering, and everyday life. Simplifying square roots allows for easier manipulation and understanding of numbers, which can be particularly useful in the following areas:
-
Mathematics:
Simplifying square roots is fundamental in algebra and calculus. It makes solving equations more straightforward and helps in understanding relationships between numbers. For example, when solving quadratic equations or integrating functions, having the square roots in their simplest form can simplify the process.
-
Physics:
In physics, square roots often appear in formulas related to wave functions, kinetic energy, and electrical engineering. Simplifying these roots can make calculations more manageable and results easier to interpret. For instance, in wave mechanics, the wavelength formula involves square roots, and simplification can help in quick problem-solving.
-
Engineering:
Engineers frequently encounter square roots in calculations involving areas, volumes, and other geometric properties. Simplifying square roots can help in designing structures, analyzing stress and strain in materials, and optimizing various engineering processes.
-
Computer Science:
Algorithms often utilize simplified square roots to optimize computations. In graphics and game development, simplified square roots can enhance performance by reducing the computational load, especially when dealing with distance calculations and transformations.
-
Finance:
In financial mathematics, simplified square roots can be useful in calculating interest rates, risk assessments, and in the modeling of financial markets. Simplifying these roots allows for clearer financial analysis and decision-making.
-
Everyday Life:
In daily life, understanding simplified square roots can assist in a variety of tasks, such as estimating measurements, solving practical problems, and making informed decisions. For example, when working on home improvement projects or when dividing resources evenly.
Overall, the simplification of square roots plays a crucial role in making complex calculations more accessible and easier to understand, thereby enhancing efficiency and accuracy in numerous applications.
Common Mistakes to Avoid
Simplifying square roots can sometimes lead to common errors. Here are some mistakes to watch out for and tips on how to avoid them:
-
Incorrect Factorization:
When simplifying, it's essential to correctly factor the number inside the square root. For example, √18 should be factored as 3√2, since 18 = 9 × 2. Incorrect factorization can lead to wrong results.
-
Ignoring the Prime Factorization:
Always break down the number into its prime factors to simplify accurately. For √18, the prime factors are 2 and 3 (i.e., 18 = 2 × 32), leading to the correct simplification: 3√2.
-
Combining Square Roots Incorrectly:
Remember that √a * √b = √(a * b). For example, √6 * √3 should be simplified to √(6 * 3) = √18 = 3√2, not calculated as √18 directly.
-
Not Simplifying Completely:
Always simplify as much as possible. For instance, √12 should be simplified to 2√3, not left as √(4 * 3).
-
Misunderstanding the Product Rule for Radicals:
Applying the product rule correctly is crucial. For example, √(a * b) = √a * √b, but it’s easy to make errors if not careful with factor pairs.
By avoiding these common mistakes, you can ensure accurate and simplified results when working with square roots.
Practice Problems
Below are some practice problems to help you master the simplification of square roots. These problems will guide you through the process step by step, ensuring you understand each part of the simplification process.
-
Find the simplified form of \(\sqrt{50}\).
Solution:
- Prime factorize 50: \(50 = 2 \times 5^2\).
- Separate the perfect squares: \(\sqrt{50} = \sqrt{2 \times 25}\).
- Simplify the perfect square: \(\sqrt{50} = 5\sqrt{2}\).
-
Simplify \(\sqrt{72}\).
Solution:
- Prime factorize 72: \(72 = 2^3 \times 3^2\).
- Separate the perfect squares: \(\sqrt{72} = \sqrt{8 \times 9}\).
- Simplify the perfect square: \(\sqrt{72} = 3\sqrt{8}\).
- Further simplify: \(8 = 2^3\), so \(\sqrt{8} = 2\sqrt{2}\).
- Final simplification: \(3 \times 2\sqrt{2} = 6\sqrt{2}\).
-
Find the simplified form of \(\sqrt{128}\).
Solution:
- Prime factorize 128: \(128 = 2^7\).
- Separate the perfect squares: \(\sqrt{128} = \sqrt{2^6 \times 2}\).
- Simplify the perfect square: \(\sqrt{128} = 2^3 \sqrt{2} = 8\sqrt{2}\).
-
Simplify \(\sqrt{200}\).
Solution:
- Prime factorize 200: \(200 = 2^3 \times 5^2\).
- Separate the perfect squares: \(\sqrt{200} = \sqrt{8 \times 25}\).
- Simplify the perfect square: \(\sqrt{200} = 5\sqrt{8}\).
- Further simplify: \(8 = 2^3\), so \(\sqrt{8} = 2\sqrt{2}\).
- Final simplification: \(5 \times 2\sqrt{2} = 10\sqrt{2}\).
-
Simplify \(\sqrt{18}\).
Solution:
- Prime factorize 18: \(18 = 2 \times 3^2\).
- Separate the perfect squares: \(\sqrt{18} = \sqrt{2 \times 9}\).
- Simplify the perfect square: \(\sqrt{18} = 3\sqrt{2}\).
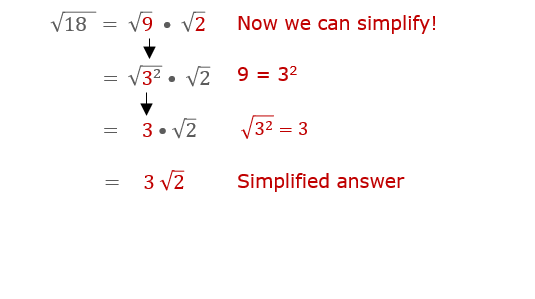
Advanced Simplification Techniques
Mastering advanced techniques for simplifying square roots can significantly enhance one's mathematical skill set. These methods go beyond the basics, offering more efficient ways to work with complex square roots.
- Denesting Square Roots: This involves simplifying expressions with nested square roots, using algebraic identities to rewrite them in a simpler form. For example, simplifying \( \sqrt{3 + 2\sqrt{2}} \) by recognizing patterns that fit the form of \((a+b)^2\).
- Conjugate Multiplication: Useful in rationalizing denominators, this technique involves multiplying the numerator and the denominator by the conjugate of the denominator to eliminate square roots in the denominator.
- Using the Binomial Theorem: For higher powers of square roots, the binomial theorem can be applied to expand and simplify expressions involving square roots.
- Algebraic Manipulation: Applying algebraic techniques such as factoring, expanding, and simplifying to rewrite square root expressions in their simplest form.
- Graphical Methods: Visualizing square root functions and their transformations can provide insights into simplifying complex square root expressions.
These advanced techniques require a solid understanding of algebra and number theory. Practicing these methods can greatly improve one's ability to simplify square roots, making it easier to solve more complex mathematical problems.
| Technique | Example |
|---|---|
| Denesting | \( \sqrt{3 + 2\sqrt{2}} \) to \(\sqrt{2} + 1\) |
| Conjugate Multiplication | \( \frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \) |
| Binomial Theorem | \( (\sqrt{x} + \sqrt{y})^2 = x + y + 2\sqrt{xy} \) |
| Algebraic Manipulation | \( \sqrt{a^2b} = a\sqrt{b} \) |
| Graphical Methods | Understanding the transformations of \( y = \sqrt{x} \) |
Additional Resources
To further enhance your understanding and proficiency in simplifying square roots, including the square root of 18, here are some valuable resources and tools:
- Online Calculators:
- - Use this tool to verify your square root simplifications.
- - Another reliable online calculator for square roots and other algebraic expressions.
- Educational Websites:
- - Offers comprehensive lessons and practice exercises on radicals and square roots.
- - Provides clear explanations and interactive examples to help understand square roots.
- Video Tutorials:
- - A step-by-step video guide on simplifying square roots.
- - Explains how to use prime factorization to simplify square roots.
- Practice Worksheets:
- - Downloadable worksheets for practicing square root simplification.
- - Free printable worksheets to test your skills.
- Books:
- - A book that covers the basics of algebra, including simplifying square roots.
- - An accessible guide to algebra concepts, including detailed sections on square roots.
These resources will help you practice and master the simplification of square roots. By exploring these tools, you can deepen your understanding and become more confident in handling square roots in various mathematical contexts.
Hướng dẫn cách đơn giản hóa căn bậc hai của 18 một cách chi tiết và dễ hiểu. Khám phá cách làm thế nào để tính căn bậc hai của số 18 một cách nhanh chóng.
Cách Đơn Giản Hóa Căn Bậc Hai Của 18: Căn(18)
READ MORE:
Video hướng dẫn cách tính và đơn giản hóa căn bậc hai của số 18 một cách chi tiết và dễ hiểu. Hãy xem để nắm vững phương pháp giải.
Căn Bậc Hai Của 18