Topic 0 squared: 0 squared, represented as \(0^2\), is a fundamental concept in mathematics. This simple yet crucial operation results in 0, providing a perfect example of how squaring a number affects it. In this article, we'll explore the significance of 0 squared, its applications, and related mathematical principles to deepen your understanding.
Table of Content
- Understanding 0 Squared
- Introduction to Squaring Numbers
- Mathematical Definition and Properties of Squaring
- Square of Zero
- Examples and Visualizations
- Perfect Squares and Their Importance
- Calculating Square Roots
- Applications of Squaring in Mathematics
- Squaring in Algebra and Calculus
- Common Misconceptions about Squaring
- Historical Context and Development
- Interactive Learning Tools for Squaring
- YOUTUBE: Khám phá lý do tại sao các số mũ 0 lại bằng 1 trong video này. Tìm hiểu nguyên lý và các ví dụ minh họa đơn giản.
Understanding 0 Squared
In mathematics, squaring a number means multiplying the number by itself. The notation for squaring a number is n2. This operation is fundamental in algebra and appears frequently in various mathematical contexts, including geometry and number theory.
Definition and Examples
When we square the number zero, we have:
- 02 = 0 × 0 = 0
This is because multiplying zero by itself results in zero.
Properties of Squaring
Squaring is a straightforward operation, but it has significant implications and properties:
- Squaring a positive number results in a positive number.
- Squaring a negative number results in a positive number.
- Squaring zero results in zero.
Geometric Interpretation
In geometry, the square of a number represents the area of a square with sides of that length. For example, a square with side length 3 has an area of:
- 32 = 3 × 3 = 9
Examples of Perfect Squares
Perfect squares are numbers that are the square of an integer. Here are some examples:
| Number | Square |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
Applications
Squaring numbers is used in various applications, such as calculating areas, solving quadratic equations, and analyzing data in statistics.

READ MORE:
Introduction to Squaring Numbers
Squaring a number involves multiplying it by itself. For instance, when we square 2, we get 4, as 2 × 2 = 4. This fundamental operation is denoted mathematically as \( 2^2 \). Squaring is not limited to integers; it applies to any real number, including decimals and fractions. Below, we delve into the various aspects of squaring numbers.
- Definition: Squaring a number means raising it to the power of 2, denoted as \( x^2 \).
- Positive and Negative Numbers: The square of a positive number is positive, and the square of a negative number is also positive because multiplying two negative numbers results in a positive product.
- Zero: Zero squared is zero, as \( 0 \times 0 = 0 \).
- Perfect Squares: Numbers like 1, 4, 9, 16, etc., are perfect squares, formed by squaring integers (1, 2, 3, 4, etc.).
- Geometric Interpretation: In geometry, the area of a square is calculated by squaring the length of one of its sides.
Squaring numbers is a basic yet crucial concept in mathematics, serving as a foundation for more advanced topics like quadratic equations, exponents, and algebraic functions.
Mathematical Definition and Properties of Squaring
Squaring a number means multiplying the number by itself. Mathematically, if n is a number, then n squared is written as n2, and calculated as n × n. For example, 2 squared is 4 because 2 × 2 = 4.
- When a positive number is squared, the result is always positive. For instance, 3 squared is 9.
- When a negative number is squared, the result is also positive. For example, (-3) squared is 9 because (-3) × (-3) = 9.
- Zero squared is zero since 0 × 0 = 0.
The properties of squaring include:
- Perfect squares: These are the squares of integers. Examples include 1, 4, 9, 16, 25, etc.
- Area calculation: The concept of squaring is often used to calculate the area of squares. For a square with side length s, the area is s2.
In mathematical notation:
\( n^2 \) means \( n \) multiplied by itself.- The square root of a number \( x \), denoted as
\( \sqrt{x} \) , is a value that, when multiplied by itself, gives \( x \).
Understanding these basic properties of squaring helps in solving algebraic equations and various mathematical problems efficiently.
Square of Zero
The square of zero is a fundamental concept in mathematics. When zero is squared, the result is always zero. This can be represented mathematically as:
\[0^2 = 0 \times 0 = 0\]
Here are some key points about squaring zero:
- Basic Property: The product of zero multiplied by itself is zero.
- Perfect Square: Zero is considered a perfect square because it can be expressed as the product of two equal integers.
- Algebraic Significance: In algebra, squaring zero can simplify equations and expressions.
The square of zero is used in various mathematical contexts, including functions, calculus, and complex number operations. Its simplicity and consistent result make it a critical concept for understanding more complex mathematical operations.
| Number | Square |
|---|---|
| 0 | 0 |
| 1 | 1 |
| -1 | 1 |
Examples and Visualizations
Understanding the concept of squaring numbers can be enhanced through various examples and visualizations. Here, we explore several scenarios to illustrate the process and implications of squaring numbers, including zero.
Basic Examples
- 0 squared: \(0^2 = 0 \times 0 = 0\)
- 1 squared: \(1^2 = 1 \times 1 = 1\)
- 2 squared: \(2^2 = 2 \times 2 = 4\)
- 3 squared: \(3^2 = 3 \times 3 = 9\)
- 4 squared: \(4^2 = 4 \times 4 = 16\)
Visualizing Squared Numbers
Visual aids can significantly enhance the comprehension of squared numbers. Below is a table showing squared values and their visual representation:
| Number | Squared Value | Visualization |
|---|---|---|
| 0 | 0 |  |
| 1 | 1 |  |
| 2 | 4 |  |
| 3 | 9 |  |
| 4 | 16 |  |
Understanding Through Graphs
Graphs are another effective way to visualize squared numbers. The graph of \(y = x^2\) shows how the values increase exponentially as x increases:
This graph illustrates that as the number gets larger, its square grows significantly, demonstrating the exponential nature of squaring.
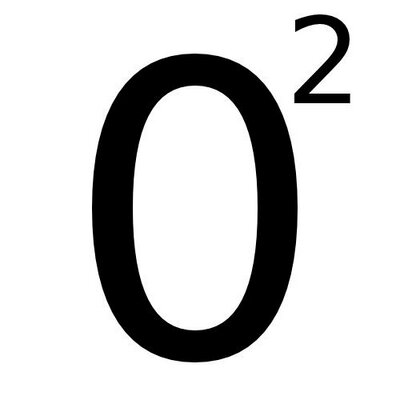
Perfect Squares and Their Importance
Perfect squares are numbers that can be expressed as the product of an integer with itself. These numbers are fundamental in various fields of mathematics and their applications extend into areas like algebra, geometry, and number theory.
For example:
- 0² = 0
- 1² = 1
- 2² = 4
- 3² = 9
- 4² = 16
- 5² = 25
- 6² = 36
- 7² = 49
- 8² = 64
- 9² = 81
- 10² = 100
These numbers are not only used for simplification and calculation purposes but also have geometric significance. A perfect square represents the area of a square with integer side lengths. Recognizing perfect squares is essential for solving quadratic equations, performing factorization, and understanding the properties of numbers.
Learning to identify and use perfect squares efficiently helps in various mathematical problems and improves number sense, making mathematical reasoning clearer and more intuitive.
Calculating Square Roots
Calculating the square root of a number is the inverse operation of squaring. The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). In mathematical notation, this is written as \( \sqrt{x} = y \). Here, we will explore the steps and methods for calculating square roots.
### Methods of Calculating Square Roots:
- Prime Factorization: Decompose the number into its prime factors and pair them to find the square root.
- Long Division Method: This traditional method involves a step-by-step division process to determine the square root.
- Using a Calculator: Modern calculators have a built-in square root function which provides quick and accurate results.
- Estimation and Approximation: For numbers that are not perfect squares, estimation techniques can be used to find an approximate value.
### Example:
To find the square root of 16 using prime factorization:
- Decompose 16 into its prime factors: \( 16 = 2 \times 2 \times 2 \times 2 \).
- Pair the prime factors: \( (2 \times 2) \times (2 \times 2) \).
- Each pair represents a factor of the square root: \( 2 \times 2 = 4 \).
- Therefore, \( \sqrt{16} = 4 \).
### Visualization:
The square root function can be visualized as the length of the side of a square with area equal to the given number. For instance, a square with area 16 units² has sides of length 4 units because \( 4^2 = 16 \).
### Special Cases:
- Square Root of 0: The square root of 0 is 0 because \( 0^2 = 0 \).
- Square Root of 1: The square root of 1 is 1 because \( 1^2 = 1 \).
- Negative Numbers: The square root of a negative number is not a real number. It involves complex numbers, represented as \( \sqrt{-x} = i\sqrt{x} \), where \( i \) is the imaginary unit.
Understanding these methods and visualizations helps in grasping the concept of square roots and their applications in various mathematical problems.
Applications of Squaring in Mathematics
Squaring is a fundamental operation in mathematics with numerous applications across various fields. Below are some key areas where squaring is applied:
-
Geometry and Area Calculation
The area of a square is calculated using the formula:
\[ A = s^2 \]
where \( s \) is the length of a side. This concept extends to calculating the area of circles and other shapes using squaring in their respective formulas.
-
Algebra
Squaring is used in algebra to solve quadratic equations of the form:
\[ ax^2 + bx + c = 0 \]
where \( a \), \( b \), and \( c \) are constants. The solutions to these equations are found using the quadratic formula:
\[ x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{2a} \]
-
Calculus
In calculus, squaring functions are used to find derivatives and integrals. For example, the derivative of \( f(x) = x^2 \) is:
\[ f'(x) = 2x \]
and the integral of \( f(x) = x^2 \) is:
\[ \int x^2 \, dx = \frac{x^3}{3} + C \]
-
Physics and Engineering
Squaring is frequently used in physics to describe relationships such as kinetic energy, given by:
\[ KE = \frac{1}{2}mv^2 \]
where \( m \) is mass and \( v \) is velocity. Squaring also appears in engineering calculations involving areas, moments of inertia, and electrical power equations.
-
Statistics
In statistics, squaring is used to calculate the variance and standard deviation, which measure the dispersion of a data set:
\[ \text{Variance} = \frac{\sum (x_i - \mu)^2}{N} \]
where \( x_i \) are data points, \( \mu \) is the mean, and \( N \) is the number of data points.
These examples demonstrate the versatility and importance of squaring in various mathematical disciplines.
Squaring in Algebra and Calculus
Squaring plays a crucial role in both algebra and calculus. Below, we explore its applications in detail:
Algebra
In algebra, squaring is often encountered when working with quadratic equations and polynomials. A quadratic equation is a second-degree polynomial of the form \( ax^2 + bx + c = 0 \). The solutions to this equation are found using various methods, including factoring, completing the square, and the quadratic formula:
\[
x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{2a}
\]
The expression \( b^2 - 4ac \) is known as the discriminant, which determines the nature of the roots:
- If \( b^2 - 4ac > 0 \), there are two distinct real roots.
- If \( b^2 - 4ac = 0 \), there is exactly one real root (a repeated root).
- If \( b^2 - 4ac < 0 \), there are two complex roots.
Example of Solving a Quadratic Equation
Consider the quadratic equation \( 5x^2 + 6x + 1 = 0 \). To solve using the quadratic formula, we identify \( a = 5 \), \( b = 6 \), and \( c = 1 \), and then substitute into the formula:
\[
x = \frac{{-6 \pm \sqrt{{6^2 - 4 \cdot 5 \cdot 1}}}}{2 \cdot 5} = \frac{{-6 \pm \sqrt{{36 - 20}}}}{10} = \frac{{-6 \pm \sqrt{16}}}{10} = \frac{{-6 \pm 4}}{10}
\]
This gives the solutions \( x = -0.2 \) and \( x = -1 \).
Calculus
In calculus, squaring functions appear frequently in differentiation and integration:
- Differentiation: The power rule is used to differentiate functions involving squares. For example, the derivative of \( f(x) = x^2 \) is \( f'(x) = 2x \).
- Integration: The integral of a squared function can be found using standard integration techniques. For instance, the integral of \( f(x) = x^2 \) is \( \int x^2 \, dx = \frac{x^3}{3} + C \), where \( C \) is the constant of integration.
Applications in Real World Problems
Squaring functions are used in a variety of real-world applications, including physics (to describe areas and volumes), economics (in cost functions), and engineering (in structural analysis). For instance, the area of a square with side length \( s \) is given by \( A = s^2 \).
Example of Integration
To find the area under the curve \( f(x) = x^2 \) from \( x = 0 \) to \( x = 2 \), we compute the definite integral:
\[
\int_0^2 x^2 \, dx = \left[ \frac{x^3}{3} \right]_0^2 = \frac{2^3}{3} - \frac{0^3}{3} = \frac{8}{3}
\]
Thus, the area under the curve is \( \frac{8}{3} \) square units.
In conclusion, squaring is a fundamental operation in algebra and calculus, essential for solving equations, modeling real-world phenomena, and performing various mathematical analyses.

Common Misconceptions about Squaring
Squaring numbers, though fundamental, often leads to several misconceptions. Addressing these misunderstandings can help solidify the concept and prevent errors in more advanced mathematics.
-
Misconception 1: The square of a number is always larger than the original number
It is commonly believed that squaring a number always results in a larger number. This is true for numbers greater than 1, but for fractions and numbers between 0 and 1, the square is smaller. For example:
\( (0.5)^2 = 0.25 \)
-
Misconception 2: Squaring a negative number yields a negative result
Some students mistakenly think that squaring a negative number results in a negative number. In reality, the square of any real number, positive or negative, is non-negative because:
\( (-3)^2 = 9 \)
-
Misconception 3: Zero is not considered in squaring operations
Another common misconception is overlooking the fact that zero can be squared, with the result being zero:
\( 0^2 = 0 \)
-
Misconception 4: Squaring a number is the same as doubling it
Some students confuse squaring a number with doubling it. These are distinct operations:
\( 3^2 = 9 \neq 3 \times 2 = 6 \)
-
Misconception 5: Squaring a fraction always results in a fraction larger than the original
For fractions less than 1, squaring results in a smaller fraction:
\( \left(\frac{1}{2}\right)^2 = \frac{1}{4} \)
By understanding and addressing these misconceptions, students can develop a stronger foundation in mathematics and avoid errors in more complex calculations involving squaring.
Historical Context and Development
The concept of squaring numbers has a rich historical background, dating back to ancient civilizations. The process of squaring a number, which means multiplying the number by itself, was understood and utilized in various cultures to solve practical problems.
One of the earliest records of squaring comes from the Babylonians around 1900-1680 BC. They used it to calculate areas, particularly in agricultural and construction contexts. Their approach was quite advanced, as evidenced by clay tablets that have been discovered, showing calculations involving squares and square roots.
In ancient Greece, the mathematician Euclid (circa 300 BC) documented the properties of squares in his seminal work, "Elements." He explored geometric interpretations of squaring, laying the groundwork for future mathematicians. Euclid's influence extended into the Islamic Golden Age, where scholars like Al-Khwarizmi (circa 800 AD) further developed algebraic techniques involving squares, which were crucial in solving quadratic equations.
Moving forward to the 17th and 18th centuries, the development of calculus by Isaac Newton and Gottfried Wilhelm Leibniz introduced new dimensions to the concept of squaring in mathematics. Squaring became fundamental in calculus, particularly in the process of differentiation and integration, where it was used to find the slopes of curves and areas under curves, respectively.
The 19th century saw significant advancements with the formalization of algebraic structures. Mathematicians like Carl Friedrich Gauss and Augustin-Louis Cauchy made substantial contributions to the understanding of quadratic forms and matrix theory, both of which involve squaring. Cauchy introduced the term "determinant" and showed its application in systems of linear equations, which often require squaring elements within matrices.
In the 20th century, squaring continued to play a crucial role in the development of modern mathematics, including the field of complex numbers. The introduction of imaginary units (\(i\)), where \(i^2 = -1\), revolutionized mathematics and engineering, providing new tools to solve equations that were previously unsolvable.
Today, squaring remains a fundamental operation in mathematics, used extensively in various branches such as algebra, calculus, geometry, and beyond. Its applications range from basic arithmetic to advanced scientific computations, reflecting its enduring importance throughout history.
Interactive Learning Tools for Squaring
Interactive learning tools can significantly enhance the understanding of mathematical concepts such as squaring. These tools provide dynamic, visual, and engaging ways to explore and practice squaring numbers. Here are some of the best interactive tools available:
-
Desmos
Desmos offers a powerful that allows students to visualize and manipulate equations involving squares. With Desmos, users can create sliders to dynamically change the value of a variable and see how its square changes in real-time.
Features include:
- Graphing quadratic functions to understand their parabolic shapes.
- Creating interactive activities where students can explore the effects of squaring on different numbers.
- Using built-in tools to demonstrate how squaring affects positive and negative numbers.
-
GeoGebra
provides a suite of tools for interactive math learning. It includes graphing calculators, geometry tools, and algebra resources that are excellent for understanding squaring.
Features include:
- Visualizing the squaring function by plotting \( y = x^2 \).
- Exploring transformations of quadratic functions.
- Interactive step-by-step problem-solving to reinforce the concept of squaring.
-
Brilliant
Brilliant.org offers interactive problem-solving courses that help students master the concept of squaring through guided lessons and exercises.
Features include:
- Interactive quizzes and problems that adapt to the learner's pace.
- Visual and intuitive explanations that make the concept of squaring easy to grasp.
- Real-time feedback to help students learn from their mistakes.
-
ICT Games
from ICT Games is an excellent tool for younger students to understand basic arithmetic operations including squaring.
Features include:
- An interactive number grid to practice squaring numbers.
- Games and puzzles that incorporate squaring in a fun way.
- Tools for teachers to use in whole-class teaching to illustrate squaring concepts.
These tools make learning about squaring numbers engaging and interactive, helping students develop a deeper understanding of the concept through practice and visualization.
Khám phá lý do tại sao các số mũ 0 lại bằng 1 trong video này. Tìm hiểu nguyên lý và các ví dụ minh họa đơn giản.
Tại sao các số mũ 0 lại bằng 1?
READ MORE:
Khám phá thách thức toán học mà 75% mọi người sẽ làm sai: (không bình phương) – (không mũ không) = ? trong video này. Thử sức với bài toán không dùng máy tính.
75% sẽ sai: (không bình phương) – (không mũ không) = ? KHÔNG SỬ DỤNG MÁY TÍNH