Topic the square root of 50: The square root of 50 is a fascinating mathematical concept that simplifies to \(5\sqrt{2}\). Discover how this irrational number plays a crucial role in various fields, from geometry to physics, and explore its properties, applications, and interesting facts. Join us as we delve into the significance and utility of the square root of 50.
Table of Content
- Square Root of 50
- Introduction
- Definition and Calculation
- Simplified Radical Form
- Properties and Characteristics
- Mathematical Applications
- Geometric Interpretations
- Comparative Analysis with Other Square Roots
- Historical Context and Discoveries
- Real-World Examples and Uses
- Advanced Mathematical Concepts Involving Square Roots
- Common Misconceptions
- FAQs
- Conclusion
- YOUTUBE: Video này hướng dẫn cách đơn giản hóa căn bậc hai của 50, giúp bạn hiểu rõ hơn về phương pháp tính toán và ứng dụng của nó trong toán học.
Square Root of 50
The square root of 50, denoted as \( \sqrt{50} \), is a mathematical expression that represents a value which, when multiplied by itself, gives the number 50. In this section, we will explore the calculation, simplification, and some interesting facts about the square root of 50.
Calculation
The square root of 50 is calculated as:
\[
\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}
\]
Therefore, \( \sqrt{50} \) can be expressed as a simplified radical form: \( 5\sqrt{2} \).
Decimal Approximation
For practical purposes, the square root of 50 can also be approximated as a decimal:
\[
\sqrt{50} \approx 7.071
\]
This value is rounded to three decimal places.
Properties of \( \sqrt{50} \)
- It is an irrational number, meaning it cannot be expressed as a simple fraction.
- It lies between the integers 7 and 8.
- It is used in various fields such as geometry, physics, and engineering.
Applications
The square root of 50 is useful in various mathematical and real-world applications, including:
- Calculating the diagonal of a square with a side length of 5 units.
- Solving problems in physics where root calculations are necessary.
- Understanding the concepts of root mean square in statistics.
Interesting Facts
- The square root of 50 is often encountered in problems involving the Pythagorean theorem.
- It can be visualized geometrically as the length of the diagonal of a rectangle with sides in the ratio of 1:5.
Table of Comparisons
| Number | Square Root |
| 49 | 7 |
| 50 | \(5\sqrt{2} \approx 7.071\) |
| 51 | 7.141 |

READ MORE:
Introduction
The square root of 50, denoted as \( \sqrt{50} \), is an important concept in mathematics. This irrational number, approximately equal to 7.071, is derived from the need to find a value that, when multiplied by itself, results in 50. The square root of 50 can be simplified to its radical form \( 5\sqrt{2} \), offering both a precise and approximate understanding.
Understanding the square root of 50 involves recognizing its properties, applications, and significance in various mathematical contexts. Whether used in geometry to determine the diagonal of a square or in physics for calculations involving roots, \( \sqrt{50} \) is a versatile and fundamental number.
- Definition and Simplification: The basic definition and how to simplify \( \sqrt{50} \) to \( 5\sqrt{2} \).
- Decimal Approximation: An approximate value of 7.071, useful for practical calculations.
- Properties: Characteristics of \( \sqrt{50} \) as an irrational number.
- Applications: Real-world uses in geometry, physics, and engineering.
By exploring these aspects, we gain a comprehensive understanding of the square root of 50 and its relevance in both theoretical and applied mathematics.
Definition and Calculation
The square root of 50, denoted as \( \sqrt{50} \), is the value that, when multiplied by itself, results in 50. This can be expressed mathematically as:
\[
\sqrt{50} \times \sqrt{50} = 50
\]
To understand this better, let's break down the calculation step-by-step:
- Prime Factorization: First, express 50 as the product of its prime factors.
\[
50 = 2 \times 5 \times 5
\] - Pairing the Prime Factors: Pair the prime factors under the square root.
\[
\sqrt{50} = \sqrt{2 \times 5^2}
\] - Simplifying the Square Root: Simplify the expression by taking out the square of the paired factor.
\[
\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}
\]
Thus, the simplified radical form of the square root of 50 is \( 5\sqrt{2} \).
Additionally, for practical purposes, we often use the decimal approximation:
\[
\sqrt{50} \approx 7.071
\]
This approximation is useful in real-world applications where a precise value is not necessary.
- Exact Form: \( 5\sqrt{2} \)
- Decimal Approximation: 7.071
By understanding both the exact and approximate values, we can apply the square root of 50 effectively in various mathematical and practical contexts.
Simplified Radical Form
The square root of 50 can be expressed in a simplified radical form, making it easier to work with in various mathematical contexts. Simplifying the radical involves breaking down the number into its prime factors and then simplifying the square root expression step-by-step.
- Prime Factorization: Start by expressing 50 as the product of its prime factors.
\[
50 = 2 \times 5^2
\] - Identify Perfect Squares: Identify any perfect squares within the prime factorization.
\[
50 = 2 \times (5^2)
\] - Simplify the Radical: Take the square root of the perfect square and move it outside the radical.
\[
\sqrt{50} = \sqrt{2 \times 5^2} = \sqrt{2} \times \sqrt{5^2} = \sqrt{2} \times 5 = 5\sqrt{2}
\]
Thus, the simplified radical form of the square root of 50 is \( 5\sqrt{2} \).
This form is more convenient for exact calculations and helps in understanding the underlying properties of the number. Here are some key points about the simplified radical form:
- Exact Value: \( 5\sqrt{2} \) represents the exact value of \( \sqrt{50} \) without approximation.
- Uses in Geometry: Simplified radicals are particularly useful in geometry, for instance, when calculating the length of the diagonal of a square with sides of 5 units.
- Mathematical Applications: The simplified form is used in algebraic operations, making it easier to add, subtract, and multiply radical expressions.
Understanding and using the simplified radical form of square roots enhances problem-solving skills and provides a clearer insight into mathematical concepts.
Properties and Characteristics
The square root of 50, \( \sqrt{50} \), exhibits several interesting properties and characteristics that are important in both theoretical and applied mathematics. Understanding these properties can provide deeper insights into its behavior and uses.
- Irrational Number:
The square root of 50 is an irrational number, meaning it cannot be expressed as a simple fraction. Its decimal form is non-repeating and non-terminating, approximately equal to 7.071.
- Simplified Radical Form:
As previously discussed, \( \sqrt{50} \) simplifies to \( 5\sqrt{2} \). This form is useful for exact calculations and provides a clearer representation of its structure.
- Algebraic Properties:
- \( (\sqrt{50})^2 = 50 \): The square of the square root of 50 returns the original number.
- \( \sqrt{50} \times \sqrt{2} = \sqrt{100} = 10 \): Demonstrates the multiplication property of square roots.
- \( \sqrt{50} \div \sqrt{2} = \sqrt{25} = 5 \): Demonstrates the division property of square roots.
- Geometric Interpretation:
In geometry, the square root of 50 can represent the length of the diagonal of a square with side lengths of 5 units. Using the Pythagorean theorem, this can be expressed as:
\[
\text{Diagonal} = \sqrt{5^2 + 5^2} = \sqrt{25 + 25} = \sqrt{50}
\] - Approximation and Usage:
While the exact value is \( 5\sqrt{2} \), the decimal approximation 7.071 is often used for practical purposes, making it easier to work with in everyday calculations.
Here is a summary table of the properties of \( \sqrt{50} \):
| Property | Value/Explanation |
| Type of Number | Irrational |
| Simplified Radical Form | \( 5\sqrt{2} \) |
| Decimal Approximation | 7.071 |
| Algebraic Properties |
|
| Geometric Interpretation | Length of the diagonal of a square with side length 5 |
Understanding these properties and characteristics of the square root of 50 enhances our ability to apply this knowledge in various mathematical and real-world contexts, providing a solid foundation for further exploration and problem-solving.

Mathematical Applications
The square root of 50, \( \sqrt{50} \), finds numerous applications in various mathematical fields and real-world scenarios. Its exact and approximate values are used to simplify calculations, solve equations, and understand geometric properties. Below are some key mathematical applications of \( \sqrt{50} \).
- Geometry:
In geometry, \( \sqrt{50} \) is often used to calculate distances and lengths. For example, the length of the diagonal of a square with sides of 5 units can be calculated as:
\[
\text{Diagonal} = \sqrt{5^2 + 5^2} = \sqrt{25 + 25} = \sqrt{50} = 5\sqrt{2}
\]This diagonal length is approximately 7.071 units.
- Algebra:
In algebra, \( \sqrt{50} \) is used to solve quadratic equations and other expressions involving square roots. For instance, in solving \( x^2 = 50 \), the solution is:
\[
x = \pm \sqrt{50} = \pm 5\sqrt{2}
\] - Trigonometry:
In trigonometry, \( \sqrt{50} \) appears in calculations involving the Pythagorean theorem and trigonometric identities. For example, finding the hypotenuse of a right triangle with legs of length 5 units each:
\[
\text{Hypotenuse} = \sqrt{5^2 + 5^2} = \sqrt{50} = 5\sqrt{2}
\] - Calculus:
In calculus, \( \sqrt{50} \) is used in integrals and derivatives involving square root functions. For example, evaluating the integral:
\[
\int \sqrt{50} \, dx = \sqrt{50} \, x + C
\]where \( C \) is the constant of integration.
- Statistics:
In statistics, \( \sqrt{50} \) can be used in calculations of standard deviation and variance where square root functions are involved. For example, the root mean square (RMS) of a set of values can involve \( \sqrt{50} \).
Below is a summary table of some of the key applications of \( \sqrt{50} \):
| Field | Application | Example |
| Geometry | Diagonal of a square | \( \sqrt{50} = 5\sqrt{2} \approx 7.071 \) |
| Algebra | Solving equations | \( x^2 = 50 \rightarrow x = \pm 5\sqrt{2} \) |
| Trigonometry | Pythagorean theorem | \( \text{Hypotenuse} = \sqrt{50} = 5\sqrt{2} \) |
| Calculus | Integrals and derivatives | \( \int \sqrt{50} \, dx = \sqrt{50} \, x + C \) |
| Statistics | Standard deviation | Root mean square calculations |
These applications demonstrate the versatility and importance of the square root of 50 in various mathematical disciplines, providing essential tools for solving a wide range of problems.
Geometric Interpretations
The square root of 50 can be understood geometrically in several ways. Let's explore some of these interpretations step by step.
Geometric Mean
One geometric interpretation of the square root of 50 is as a geometric mean. If you have two segments of lengths 10 and 5, the square root of 50 is the length of a segment such that the ratio of the segments is equal:
\(\sqrt{50} = \sqrt{10 \times 5} = \sqrt{10 \cdot 5}\)
Right Triangle
Another interpretation involves a right triangle. Consider a right triangle with legs of lengths 5 and 5. The length of the hypotenuse of this triangle is the square root of 50:
\[
\text{Hypotenuse} = \sqrt{5^2 + 5^2} = \sqrt{25 + 25} = \sqrt{50}
\]
This can be visualized as follows:

|
Square Construction
Imagine a square with an area of 50 square units. The length of each side of this square is the square root of 50. To find this length, you use the formula for the area of a square, where the side length \(s\) is:
\[
s = \sqrt{50}
\]
Therefore, if you construct a square with this side length, you can better understand the geometric significance of the square root of 50.
Diagonal of a Rectangle
The square root of 50 can also be the length of the diagonal of a rectangle. Consider a rectangle with sides of lengths 5 and 10 units. The length of the diagonal \(d\) is given by:
\[
d = \sqrt{5^2 + 10^2} = \sqrt{25 + 100} = \sqrt{125} = 5\sqrt{5}
\]
To find a rectangle whose diagonal is exactly \(\sqrt{50}\), you can scale down the side lengths accordingly.
Circle and Radius
If you inscribe a square within a circle such that the diameter of the circle is the diagonal of the square, and the area of the square is 50 square units, then the diameter of the circle is \(\sqrt{50}\). The radius \(r\) of the circle would be:
\[
r = \frac{\sqrt{50}}{2}
\]
Visualization through Graphs
To better understand these interpretations, visualizing the geometric shapes and constructions on graph paper or using software tools can be very helpful. Below is a graphical representation of some of these geometric interpretations:

|
Through these geometric interpretations, the square root of 50 can be seen not just as a numerical value but as a concept that can be visualized and understood in various practical and theoretical contexts.
Comparative Analysis with Other Square Roots
The square root of 50 can be compared with other square roots to understand its unique properties and value in different mathematical contexts. Below, we will examine how the square root of 50 compares to other square roots, both smaller and larger.
Comparison with Perfect Squares
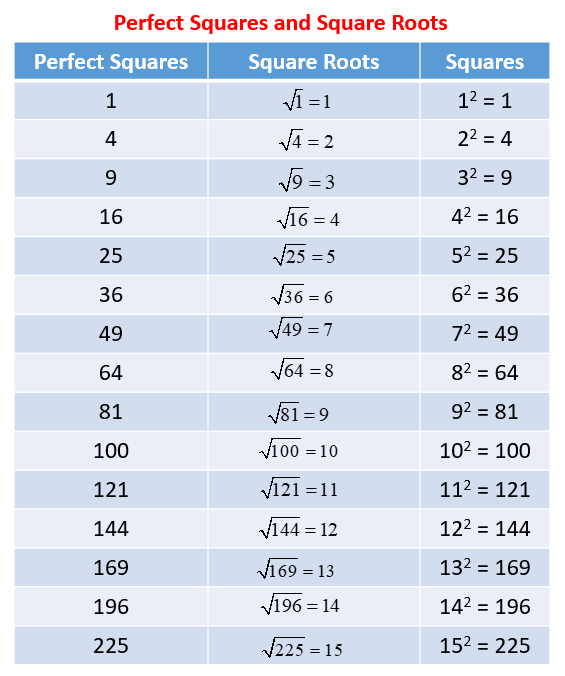
The square root of 50 is not a perfect square, unlike the square roots of 49 and 64. This makes its value an irrational number, specifically:
- √49 = 7
- √50 ≈ 7.071
- √64 = 8
As seen, √50 (approximately 7.071) lies between the whole numbers 7 and 8, showing it is slightly more than 7 but less than 8.
Radical Form Comparison
Expressing the square roots in their simplified radical forms:
- √49 = 7
- √50 = 5√2
- √64 = 8
Here, √50 in its simplified radical form (5√2) demonstrates its non-integer nature, differing from the integers derived from perfect squares.
Decimal Comparison
When comparing the decimal approximations of the square roots of some other non-perfect squares close to 50:
- √45 ≈ 6.708
- √50 ≈ 7.071
- √55 ≈ 7.416
The square root of 50 is clearly higher than √45 and lower than √55, showing a gradual increase in value.
Properties and Characteristics
The square root of 50 shares some properties with other square roots:
- It is an irrational number, meaning it cannot be expressed as a simple fraction.
- Its decimal expansion is non-terminating and non-repeating.
- Like other square roots of non-perfect squares, it is useful in various calculations and geometric interpretations.
Mathematical Context
In mathematical contexts, comparing the square root of 50 with other roots can be insightful. For example:
- The square root of 49 (7) is often used in simple geometric calculations involving squares.
- The square root of 50 (≈7.071) is used in more complex geometrical interpretations, often involving diagonal distances and approximations.
- The square root of 64 (8) represents another perfect square, showing a distinct step up from √50 in terms of simplicity and ease of calculation.
Conclusion
Understanding the square root of 50 in comparison to other square roots helps highlight its unique properties as an irrational number. While it is close to simple integer roots like 7 and 8, its exact value (7.071) and radical form (5√2) demonstrate the complexity and beauty of non-perfect square roots in mathematics.
Historical Context and Discoveries
The concept of square roots dates back to ancient civilizations, including the Egyptians and Babylonians, who utilized rudimentary methods to estimate these values. The square root of 50, like many other numbers, has a rich historical significance.
One of the earliest known references to geometric principles that include the concept of square roots comes from the work of ancient Indian mathematicians. The Sulbasutras, ancient Indian texts on geometry, contain various rules for constructing altars and religious structures, and implicitly involve calculations of square roots. Notably, the work of Baudhāyana around 800 BCE includes an approximation of the diagonal of a square, which is related to the concept of square roots. Specifically, Baudhāyana's Sulbasutra includes what is now known as the Pythagorean theorem, stating that the area produced by the diagonal of a square is equal to the sum of the areas produced by its sides.
In the context of square roots, this ancient understanding indicates an awareness of the properties of irrational numbers, as the square root of non-perfect squares like 50 would have been understood in terms of these geometric constructions. Baudhāyana’s work shows that these ancient mathematicians were capable of approximating irrational numbers through geometric means.
Moving forward in history, Greek mathematicians such as Euclid further formalized the study of square roots. Euclid's Elements, written around 300 BCE, include systematic methods for determining square roots and properties of numbers. Although Euclid did not explicitly calculate the square root of 50, his principles laid the groundwork for understanding such computations.
During the Islamic Golden Age, scholars such as Al-Khwarizmi continued to build on these foundations. Al-Khwarizmi’s work on algebra and arithmetic in the 9th century included methods for solving quadratic equations, which naturally led to the extraction of square roots. His methods would influence both the Islamic world and later European mathematics.
In the Renaissance period, European mathematicians like Leonardo of Pisa, known as Fibonacci, reintroduced and expanded upon these classical methods. The development of more sophisticated notation and arithmetic during this period made the calculation of square roots more accessible and accurate. Fibonacci’s work in "Liber Abaci" (1202) includes techniques for approximating square roots, including that of 50.
In summary, the historical context of the square root of 50 reveals a journey from ancient geometric approximations to more formalized algebraic methods. This evolution reflects the broader development of mathematical thought and its increasing precision over millennia.
Real-World Examples and Uses
The square root of 50, like other square roots, finds application in various real-world contexts. Here are some examples and uses:
-
Engineering:
Square roots are crucial in engineering, particularly when dealing with stress and strain calculations in materials. For example, the formula for calculating the standard deviation of stress involves square roots, which helps engineers determine the reliability and safety of materials used in construction.
-
Architecture:
In architecture, the Pythagorean theorem is frequently used to calculate distances and design elements, which involves square roots. For instance, when determining the length of a diagonal support beam in a rectangular frame, architects use the square root to find the correct length.
-
Finance:
Square roots are used in financial calculations such as determining the volatility of stock prices. The standard deviation, a measure of volatility, involves taking the square root of the variance of returns, which helps investors assess risk.
-
Physics:
In physics, the square root function is used to calculate root mean square (RMS) values of alternating current (AC) voltages and currents, which is essential for designing and analyzing electrical circuits.
-
Statistics:
Square roots are integral in statistics, especially in the calculation of standard deviation and variance. These measures help in understanding the spread and distribution of data points in a dataset, which is essential for data analysis and decision-making.
-
Geometry:
In geometry, square roots are used to determine distances between points in coordinate systems. For example, the distance formula, which is derived from the Pythagorean theorem, involves taking the square root of the sum of the squares of the differences between the coordinates.
-
Computer Science:
Square roots are used in algorithms for tasks such as calculating distances in spatial databases, image processing, and various computational geometry problems. For instance, the Euclidean distance formula used in clustering algorithms involves square roots.
-
Navigation:
Square roots help in navigation and GPS calculations to determine the shortest path between two points. The Haversine formula, which calculates the great-circle distance between two points on a sphere, involves square roots.
These examples illustrate the diverse applications of square roots in different fields, highlighting their importance in solving real-world problems and making informed decisions.
Advanced Mathematical Concepts Involving Square Roots
The square root function, denoted as \( \sqrt{x} \), is a fundamental mathematical operation with a variety of advanced applications and properties. Below are detailed discussions of some advanced mathematical concepts involving square roots:
1. Properties of the Square Root Function
- Non-Negative Output: The square root function returns the non-negative root of a non-negative input. For any real number \( x \geq 0 \), \( \sqrt{x} \geq 0 \).
- Non-Linear Function: The square root function is non-linear, as its rate of change decreases with increasing values of \( x \). This property is evident in its graph, which is a curved line that increases at a decreasing rate.
- Domain and Range: The domain of the square root function is all non-negative real numbers \([0, \infty)\), and its range is also all non-negative real numbers \([0, \infty)\).
2. Complex Numbers
When dealing with negative numbers, the square root function extends to complex numbers. The square root of a negative number \( -x \) is \( \sqrt{-x} = i\sqrt{x} \), where \( i \) is the imaginary unit. This extension is crucial in many fields, including engineering and physics.
3. Solving Quadratic Equations
The square root function is integral in solving quadratic equations of the form \( ax^2 + bx + c = 0 \). Using the quadratic formula \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \), the discriminant \( b^2 - 4ac \) determines the nature of the roots:
- If \( b^2 - 4ac > 0 \), the equation has two distinct real roots.
- If \( b^2 - 4ac = 0 \), the equation has one real root (a repeated root).
- If \( b^2 - 4ac < 0 \), the equation has two complex roots.
4. Differential Equations
Square roots frequently appear in solutions to differential equations. For example, the solution to the differential equation \( \frac{dy}{dx} = k \sqrt{y} \) involves separating variables and integrating, leading to solutions that involve square root functions.
5. Eigenvalues and Eigenvectors
In linear algebra, the computation of eigenvalues often involves square roots. Given a matrix \( A \), the eigenvalues are solutions to the characteristic equation \( \det(A - \lambda I) = 0 \), which may involve square root terms when solved.
6. Geometric Interpretations
Square roots are essential in geometry, particularly in the Pythagorean theorem. For a right triangle with legs \( a \) and \( b \) and hypotenuse \( c \), the theorem states \( c = \sqrt{a^2 + b^2} \). This relationship is foundational in Euclidean geometry.
7. Statistical Analysis
In statistics, the square root function is used to calculate the standard deviation, \( \sigma \), from the variance \( \sigma^2 \). The standard deviation, given by \( \sigma = \sqrt{\sigma^2} \), measures the dispersion of a dataset.
8. Signal Processing
Square roots are used in signal processing for calculating RMS (Root Mean Square) values. RMS is a statistical measure of the magnitude of a varying quantity and is given by \( \text{RMS} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} x_i^2} \).
These advanced concepts illustrate the extensive applications and significance of square roots in various mathematical, scientific, and engineering fields.
Common Misconceptions
When dealing with the square root of 50, several common misconceptions can arise. Understanding and addressing these misconceptions is crucial for a clearer grasp of mathematical concepts involving square roots.
- Misinterpretation of Simplified Radical Form: A common mistake is incorrectly simplifying the square root of 50. The correct simplification is:
Some students might forget to factorize 50 correctly and end up with incorrect simplifications.
\[ \sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2} \] - Confusion with Decimal Approximation: Another frequent error is assuming that the square root of 50, approximately 7.071, is an exact value. This is a rounded value, and the precise value is irrational, meaning it cannot be expressed as a simple fraction and has a non-terminating, non-repeating decimal expansion.
- Mixing Square Roots and Squares: Students sometimes mix up the operations of squaring a number and taking the square root. For example, they might incorrectly think that:
while actually, it is true but the confusion lies when they assume square root and squares nullify each other without understanding the underlying properties.
\[ (\sqrt{50})^2 = 50 \] - Misunderstanding the Nature of Surds: Surds, or irrational roots, like \(\sqrt{50}\), are often misunderstood. Students might mistakenly believe they can be simplified to rational numbers, or they might incorrectly add or subtract surds. Proper handling requires recognizing that:
But different radicands cannot be combined this way (e.g., \(\sqrt{2} + \sqrt{3} \neq \sqrt{5}\)).
\[ a\sqrt{b} + c\sqrt{b} = (a + c)\sqrt{b} \] - Incorrect Application in Equations: When solving equations involving square roots, a common mistake is neglecting to consider both the positive and negative roots. For example, solving:
should yield:
\[ x^2 = 50 \]
Both \( \sqrt{50} \) and \( -\sqrt{50} \) are solutions.
\[ x = \pm \sqrt{50} \]
By recognizing and addressing these common misconceptions, students can develop a stronger, more accurate understanding of the mathematical principles involving square roots.
FAQs
Below are some frequently asked questions about the square root of 50:
- What is the value of the square root of 50?
The square root of 50 is approximately 7.07106781187.
- Is the square root of 50 a rational number?
No, the square root of 50 is an irrational number because it cannot be expressed as a fraction of two integers and its decimal representation is non-terminating and non-repeating.
- How is the square root of 50 simplified?
The square root of 50 can be simplified to 5√2, where 5 is a rational number and √2 is an irrational number.
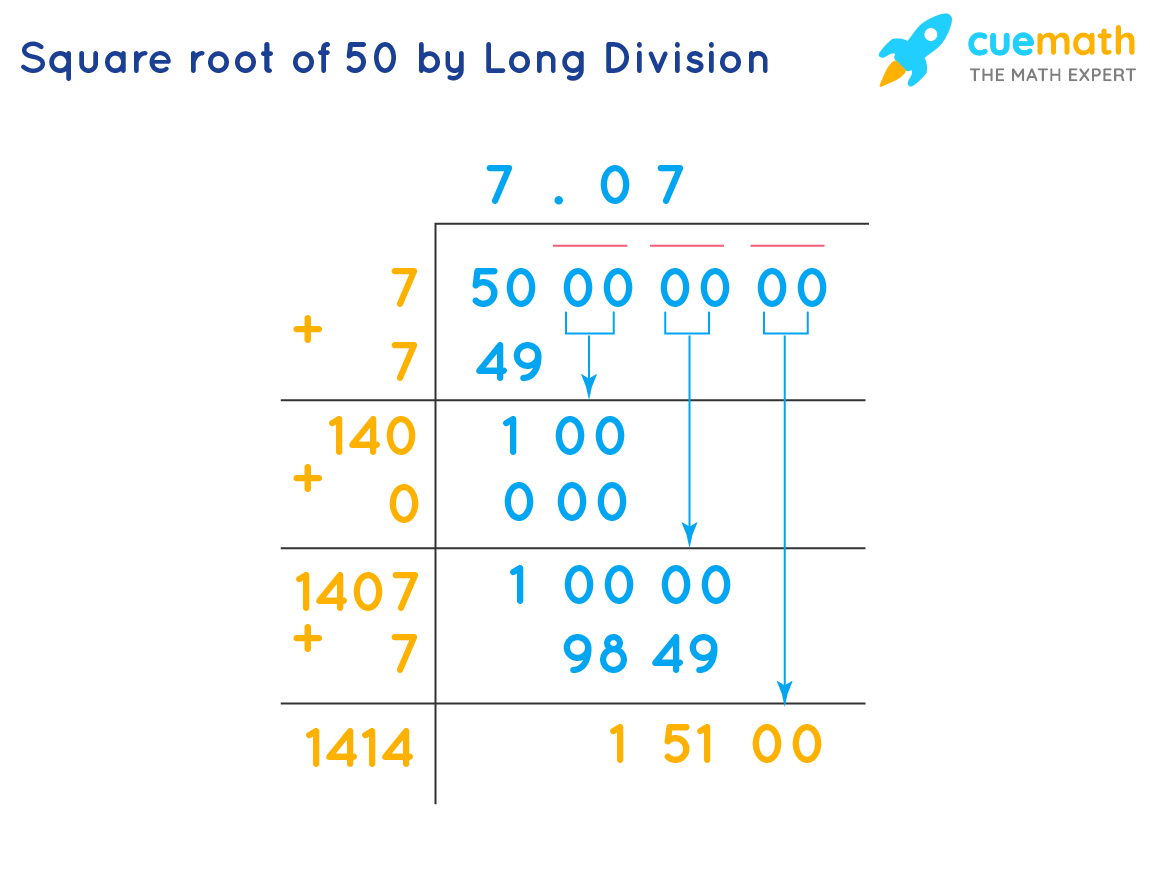
- What are some methods to calculate the square root of 50?
- Prime Factorization Method: Decompose 50 into prime factors (2 × 5 × 5), then simplify under the radical.
- Long Division Method: Use iterative long division to approximate the square root to the desired precision.
- Estimation Method: Recognize that 50 is between the squares of 7 and 8, so its square root is between 7 and 8.
- Babylonian Method (Heron’s Method): Use iterative averaging to refine an initial guess.
- Can the square root of 50 be negative?
Yes, the square root of 50 has two values: +7.07106781187 and -7.07106781187, but typically the positive value is referred to as the principal square root.
- What is the inverse operation of taking the square root of 50?
The inverse operation of taking the square root is squaring. So, squaring the square root of 50 (7.07106781187) returns the original number 50.
If you have any other questions about the square root of 50, feel free to ask!

Conclusion
The square root of 50, denoted as \( \sqrt{50} \), is a fascinating mathematical concept with multiple representations and applications. In its simplest radical form, it is expressed as \( 5\sqrt{2} \), highlighting its relationship with the irrational number \( \sqrt{2} \). The decimal approximation of \( \sqrt{50} \) is approximately 7.071, making it clear that 50 is not a perfect square.
Understanding the square root of 50 involves various mathematical techniques, including prime factorization and the long division method. These methods not only help in finding the square root but also in comprehending the nature of irrational numbers.
The exploration of \( \sqrt{50} \) demonstrates its significance in both theoretical and practical contexts. From geometric interpretations to advanced mathematical applications, the square root of 50 serves as an essential element in the broader scope of mathematics.
By examining its properties and applications, one gains a deeper appreciation for the intricacies of square roots and their role in various fields. Whether for academic purposes or real-world problem-solving, the square root of 50 provides valuable insights and demonstrates the beauty of mathematical relationships.
Video này hướng dẫn cách đơn giản hóa căn bậc hai của 50, giúp bạn hiểu rõ hơn về phương pháp tính toán và ứng dụng của nó trong toán học.
Cách Đơn Giản Hóa Căn Bậc Hai Của 50: Sqrt(50)
READ MORE:
Video này hướng dẫn cách đơn giản hóa căn bậc hai của một số, đặc biệt là căn bậc hai của 50, giúp bạn hiểu rõ hơn về phương pháp tính toán và ứng dụng của nó trong toán học.
Đơn Giản Hóa Căn Bậc Hai Của Một Số | Đơn Giản Hóa Toán Học, Căn Bậc Hai Của 50