Is the Square Root of 50 a Rational Number? Discover the Truth!

Based on the search results from Bing:

1. The square root of 50, √50, is an irrational number because it cannot be expressed as a ratio of two integers.
2. It is a non-repeating, non-terminating decimal.
3. Mathematically, an irrational number like √50 cannot be written in the form p/q where p and q are integers and q is not zero.
4. There are no common factors between the numbers under the square root, 50, making it an irrational number.

Understanding the distinction between rational and irrational numbers is fundamental in mathematics. These classifications help us identify the nature of different types of numbers.

Rational Numbers are numbers that can be expressed as the quotient or fraction of two integers, where the numerator is an integer and the denominator is a non-zero integer. Formally, a number \( \frac{a}{b} \) is rational if \( a \) and \( b \) are integers and \( b \neq 0 \). Rational numbers can be either positive or negative and include integers, finite decimals, and repeating decimals.

Examples of rational numbers:

• \( \frac{1}{2} \) (0.5)
• \( -3 \) (an integer)
• \( \frac{22}{7} \) (approximately 3.142857, a repeating decimal)

Irrational Numbers are numbers that cannot be expressed as a simple fraction. Their decimal expansions are non-repeating and non-terminating. These numbers cannot be written as the ratio of two integers.

Examples of irrational numbers:

• \( \sqrt{2} \) (approximately 1.414213...)
• \( \pi \) (approximately 3.141592...)
• \( e \) (approximately 2.718281...)

The distinction between rational and irrational numbers helps in various mathematical applications and problem-solving scenarios.

Rational numbers are a fundamental concept in mathematics. These numbers can be defined and characterized by specific properties that distinguish them from other types of numbers.

Definition: A rational number is any number that can be expressed as the quotient or fraction \( \frac{a}{b} \) of two integers, where \( a \) (the numerator) and \( b \) (the denominator) are integers, and \( b \neq 0 \). In mathematical notation, it is represented as:

\[ \text{Rational Number} = \frac{a}{b} \quad \text{where} \quad a, b \in \mathbb{Z}, \, b \neq 0 \]

Properties of Rational Numbers:

1. Closure Property: Rational numbers are closed under addition, subtraction, multiplication, and division (except by zero). This means that performing these operations on rational numbers will always yield a rational number.
2. Commutative Property: Rational numbers follow the commutative property for addition and multiplication: \[ a + b = b + a \] \[ a \times b = b \times a \]
3. Associative Property: Rational numbers follow the associative property for addition and multiplication: \[ (a + b) + c = a + (b + c) \] \[ (a \times b) \times c = a \times (b \times c) \]
4. Distributive Property: Rational numbers follow the distributive property of multiplication over addition: \[ a \times (b + c) = (a \times b) + (a \times c) \]
5. Density Property: Between any two rational numbers, there exists another rational number. For example, between \( \frac{1}{2} \) and \( \frac{3}{4} \), there is \( \frac{5}{8} \).
6. Decimal Representation: Rational numbers can be represented as either terminating or repeating decimals. For example:
   • \( \frac{1}{2} = 0.5 \) (terminating)
   • \( \frac{1}{3} = 0.333\ldots \) (repeating)

Understanding these properties helps in recognizing and working with rational numbers in various mathematical contexts.

Irrational numbers are an important category of real numbers that possess unique characteristics. Understanding these numbers is crucial for grasping more advanced mathematical concepts.

Definition: An irrational number is a number that cannot be expressed as a simple fraction \( \frac{a}{b} \), where \( a \) and \( b \) are integers and \( b \neq 0 \). The decimal representation of an irrational number is non-terminating and non-repeating. In mathematical notation, it is represented as:

\[ \text{Irrational Number} \neq \frac{a}{b} \quad \text{where} \quad a, b \in \mathbb{Z}, \, b \neq 0 \]

Properties of Irrational Numbers:

1. Non-Terminating and Non-Repeating Decimals: Irrational numbers have infinite decimal expansions that do not repeat a fixed sequence of digits. For example:
   • \( \pi = 3.141592653589793\ldots \)
   • \( \sqrt{2} = 1.414213562373095\ldots \)
2. Cannot Be Expressed as Fractions: By definition, irrational numbers cannot be written as the quotient of two integers. This distinguishes them from rational numbers, which can always be expressed as fractions.
3. Density Property: Just like rational numbers, irrational numbers are densely populated on the real number line. This means that between any two real numbers, there is always an irrational number.
4. Closure Property: Unlike rational numbers, irrational numbers are not closed under standard arithmetic operations. For example:
   • The sum of two irrational numbers can be rational or irrational. (e.g., \( \sqrt{2} + (-\sqrt{2}) = 0 \) which is rational)
   • The product of two irrational numbers can be rational or irrational. (e.g., \( \sqrt{2} \times \sqrt{2} = 2 \) which is rational)

Irrational numbers play a significant role in various fields such as geometry, calculus, and trigonometry, where they are often encountered as the lengths of certain lines, values of functions, and solutions to equations.

The square root of 50 is an important mathematical concept, particularly in the context of rational and irrational numbers. To fully grasp its nature, we need to delve into its properties and representation.

Calculation: The square root of 50, denoted as \( \sqrt{50} \), is the number that, when multiplied by itself, gives 50. Mathematically, this is expressed as:

\[ \sqrt{50} \times \sqrt{50} = 50 \]

Simplification: The square root of 50 can be simplified by expressing it in terms of prime factors. The prime factorization of 50 is:

\[ 50 = 2 \times 5^2 \]

Therefore, we can write:

\[ \sqrt{50} = \sqrt{2 \times 5^2} = \sqrt{2} \times \sqrt{25} = \sqrt{2} \times 5 = 5\sqrt{2} \]

Decimal Representation: The square root of 50 is an irrational number because it cannot be expressed as a simple fraction. Its decimal representation is non-terminating and non-repeating:

\[ \sqrt{50} \approx 7.0710678118654755\ldots \]

Nature as an Irrational Number: Since \( \sqrt{50} \) cannot be written as \( \frac{a}{b} \) where \( a \) and \( b \) are integers and \( b \neq 0 \), it is classified as an irrational number. This is due to the presence of \( \sqrt{2} \) in its simplified form, which is known to be irrational.

Geometric Interpretation: In geometry, the length of the diagonal of a rectangle with sides 5 and 5 units is \( \sqrt{50} \). This length cannot be precisely measured using a simple fraction, further illustrating its irrational nature.

Understanding the square root of 50 involves recognizing its properties, its representation in decimal form, and its classification as an irrational number. This knowledge is essential for deeper mathematical exploration and problem-solving.

To prove that the square root of 50 is an irrational number, we can use a proof by contradiction. The goal is to demonstrate that \( \sqrt{50} \) cannot be expressed as a fraction of two integers.

Step-by-Step Proof:

1. Assume, for the sake of contradiction, that \( \sqrt{50} \) is rational. This means it can be expressed as a fraction \( \frac{a}{b} \), where \( a \) and \( b \) are integers with no common factors other than 1 (i.e., \( \frac{a}{b} \) is in its simplest form), and \( b \neq 0 \).
2. If \( \sqrt{50} = \frac{a}{b} \), then squaring both sides of the equation gives: \[ 50 = \frac{a^2}{b^2} \]
3. By multiplying both sides by \( b^2 \), we get: \[ 50b^2 = a^2 \]
4. This equation implies that \( a^2 \) is divisible by 50. Since 50 can be factored into prime numbers as \( 50 = 2 \times 5^2 \), \( a^2 \) must be divisible by both 2 and \( 5^2 \).
5. For \( a^2 \) to be divisible by \( 5^2 \), \( a \) itself must be divisible by 5 (since the square of a number divisible by 5 must be divisible by \( 5^2 \)). Let \( a = 5k \), where \( k \) is an integer.
6. Substituting \( a = 5k \) into the equation \( 50b^2 = a^2 \) gives: \[ 50b^2 = (5k)^2 \] \[ 50b^2 = 25k^2 \]
7. Dividing both sides by 25, we get: \[ 2b^2 = k^2 \]
8. This equation implies that \( k^2 \) is divisible by 2, which means \( k \) must be divisible by 2 (since the square of a number divisible by 2 must be divisible by 2). Let \( k = 2m \), where \( m \) is an integer.
9. Substituting \( k = 2m \) into the equation \( 2b^2 = k^2 \) gives: \[ 2b^2 = (2m)^2 \] \[ 2b^2 = 4m^2 \]
10. Dividing both sides by 2, we get: \[ b^2 = 2m^2 \]
11. This equation implies that \( b^2 \) is divisible by 2, which means \( b \) must be divisible by 2.
12. Now, we have shown that both \( a \) and \( b \) are divisible by 2, which contradicts our initial assumption that \( \frac{a}{b} \) is in its simplest form (i.e., \( a \) and \( b \) have no common factors other than 1).

Since our assumption that \( \sqrt{50} \) is rational leads to a contradiction, we conclude that \( \sqrt{50} \) is irrational. This proof demonstrates that \( \sqrt{50} \) cannot be expressed as a fraction of two integers, solidifying its status as an irrational number.

Understanding the square root of 50 in comparison to other square roots helps to contextualize its properties and significance. Here, we compare \( \sqrt{50} \) with square roots of both rational and irrational numbers.

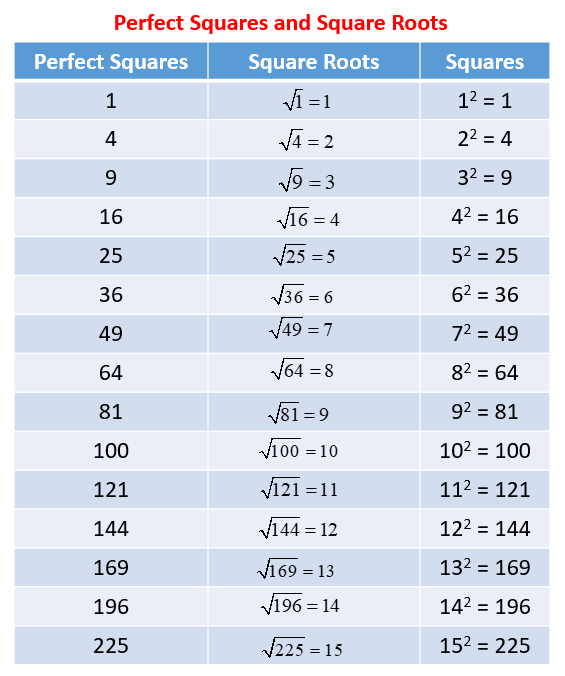
Square Roots of Perfect Squares: Perfect squares are numbers whose square roots are integers, hence rational. Examples include:

• \( \sqrt{1} = 1 \)
• \( \sqrt{4} = 2 \)
• \( \sqrt{9} = 3 \)
• \( \sqrt{16} = 4 \)
• \( \sqrt{25} = 5 \)

These square roots can be expressed as simple fractions and are therefore rational numbers.

Square Roots of Non-Perfect Squares: Numbers that are not perfect squares have square roots that are irrational. These include:

• \( \sqrt{2} \approx 1.414213 \)
• \( \sqrt{3} \approx 1.732050 \)
• \( \sqrt{5} \approx 2.236067 \)
• \( \sqrt{7} \approx 2.645751 \)
• \( \sqrt{11} \approx 3.316624 \)

The square root of 50 falls into this category of non-perfect squares and is therefore irrational.

Comparison with Other Irrational Square Roots:

• \( \sqrt{50} = 5\sqrt{2} \approx 7.071068 \)
• \( \sqrt{45} = 3\sqrt{5} \approx 6.708204 \)
• \( \sqrt{18} = 3\sqrt{2} \approx 4.242641 \)
• \( \sqrt{20} = 2\sqrt{5} \approx 4.472136 \)

As seen, irrational square roots often involve the square roots of prime factors. The presence of these prime factors leads to non-terminating, non-repeating decimals, confirming their irrationality.

Geometric Interpretation: Geometrically, the length of a diagonal in a square or rectangle often involves irrational square roots. For instance, the diagonal of a square with side length 1 is \( \sqrt{2} \), and for a rectangle with sides 5 and 5, the diagonal is \( \sqrt{50} \).

In summary, the square root of 50 is a prime example of an irrational number when compared with both rational and other irrational square roots. This understanding is crucial in both theoretical and applied mathematics.

The concepts of rational and irrational numbers have deep historical roots, dating back to ancient civilizations. Understanding their development provides valuable insights into the evolution of mathematical thought.

Ancient Greece: The ancient Greeks were among the first to explore the properties of rational and irrational numbers. Pythagoras and his followers initially believed that all numbers could be expressed as ratios of integers (rational numbers). This belief was central to their philosophy that "all is number."

However, the discovery of irrational numbers is attributed to the Pythagorean school. The legend goes that Hippasus, a Pythagorean, discovered that the diagonal of a square with side length 1 could not be expressed as a ratio of two integers. This diagonal is \( \sqrt{2} \), an irrational number. This discovery was so shocking to the Pythagoreans that, according to some accounts, Hippasus was punished or even killed for revealing this mathematical truth.

Classical Era: Following the initial shock, Greek mathematicians like Euclid began to study irrational numbers more systematically. In his work "Elements," Euclid provided a proof of the irrationality of \( \sqrt{2} \) and discussed other irrational magnitudes. His work laid the foundation for understanding irrational numbers as legitimate mathematical entities.

Medieval Islamic Mathematics: Islamic mathematicians made significant contributions to the study of numbers. Al-Khwarizmi and others translated and expanded upon Greek works, further developing the concept of irrational numbers. They also made advances in algebra, which provided new ways to understand and work with both rational and irrational numbers.

Renaissance and Enlightenment: During the Renaissance, the revival of Greek mathematical texts led to renewed interest in irrational numbers. Mathematicians like Rafael Bombelli and Simon Stevin worked on the arithmetic of irrational numbers, making them more accessible and understandable.

In the 17th century, the development of calculus by Newton and Leibniz further integrated irrational numbers into mainstream mathematics. Calculus relied heavily on the use of real numbers, which include both rational and irrational numbers.

Modern Era: The formal definition of irrational numbers and their properties were solidified in the 19th and 20th centuries. Mathematicians like Richard Dedekind and Georg Cantor developed rigorous foundations for real numbers, including both rational and irrational numbers. Cantor's work on set theory and the real number line clarified the relationship between these two classes of numbers.

Today, the study of rational and irrational numbers is fundamental to various fields of mathematics and science. Understanding their historical development helps appreciate the depth and richness of mathematical concepts that are now taken for granted.

Rational and irrational numbers are not just abstract concepts; they have numerous real-life applications that are fundamental to various fields. Understanding these applications highlights the importance of both types of numbers in our daily lives and in scientific advancements.

Applications of Rational Numbers:

• Finance and Economics: Rational numbers are used to represent quantities of money, interest rates, and financial ratios. For example, fractions and decimals are used in calculating taxes, budgeting, and analyzing economic trends.
• Engineering: Rational numbers are crucial in engineering for precise measurements, construction, and design. They are used to define proportions, scales, and tolerances in engineering projects.
• Cooking and Baking: Recipes often require ingredients to be measured in specific ratios. Rational numbers ensure accuracy in the amount of each ingredient used, which is essential for achieving the desired taste and consistency.
• Time Measurement: Time is often expressed in rational numbers, such as hours, minutes, and seconds. Scheduling, time management, and synchronization of events rely on rational numbers for precision.

Applications of Irrational Numbers:

• Geometry and Trigonometry: Irrational numbers frequently appear in geometric calculations, such as finding the lengths of diagonals, areas of circles, and angles. For example, the number \( \pi \) is used to calculate the circumference and area of circles.
• Physics: Many physical constants are irrational numbers. For instance, the speed of light, Planck's constant, and the gravitational constant often involve irrational values when expressed in certain units. These constants are fundamental to the laws of physics and engineering calculations.
• Art and Architecture: The golden ratio, an irrational number approximately equal to 1.618, is used in art and architecture to create aesthetically pleasing designs. It appears in the proportions of famous structures and artworks.
• Music: The frequencies of musical notes can involve irrational numbers. The equal temperament tuning system, which divides an octave into 12 equal parts, results in irrational ratios between the frequencies of notes.

Combination of Rational and Irrational Numbers:

In many real-life applications, both rational and irrational numbers are used together to achieve precise and practical results. For instance:

• In computer graphics, rendering images often requires calculations involving both rational and irrational numbers to achieve realistic effects.
• In navigation and GPS technology, coordinates and distances may involve a mix of rational and irrational numbers to pinpoint locations accurately.

Understanding the applications of rational and irrational numbers helps in appreciating their significance beyond theoretical mathematics. They play a crucial role in various disciplines, contributing to advancements in technology, science, and the arts.

There are several common misconceptions about rational and irrational numbers. Understanding these misconceptions is crucial for a clearer grasp of the nature of these numbers.

• Misconception 1: All non-integer numbers are irrational

  Many people believe that if a number is not a whole number, it must be irrational. This is incorrect. Rational numbers include fractions and decimals that terminate or repeat. For example, 0.5 (which is 1/2) and 0.333... (which is 1/3) are both rational.

• Misconception 2: Irrational numbers cannot be represented as decimals

  While irrational numbers cannot be expressed as a finite or repeating decimal, they can still be represented in decimal form. The key characteristic of an irrational number's decimal expansion is that it is non-terminating and non-repeating. For example, the square root of 2 is approximately 1.414213..., and it does not repeat or terminate.

• Misconception 3: Rational and irrational numbers are not related

  Another misconception is that rational and irrational numbers are entirely separate entities. In reality, they both fit into the larger category of real numbers. Together, rational and irrational numbers fill the entire number line without any gaps.

• Misconception 4: There are more rational numbers than irrational numbers

  It might seem intuitive to think there are more rational numbers since we can easily list fractions and integers. However, in terms of cardinality, the set of irrational numbers is much larger. The rational numbers are countable, whereas the irrational numbers are uncountable.

• Misconception 5: The square root of a non-perfect square is always irrational

  While it is true that the square roots of most non-perfect squares are irrational, there are exceptions, particularly in the context of simplifying radicals. For instance, \( \sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2} \), where \( \sqrt{2} \) is irrational, but 50 itself isn't considered for rationality or irrationality.

• Misconception 6: Only positive numbers can be irrational

  Negative numbers can also be irrational. For instance, \(-\sqrt{2}\) and \(-\pi\) are irrational numbers. The irrational nature of a number is not affected by its sign.

By addressing these misconceptions, we can better understand the true nature and characteristics of rational and irrational numbers.

The square root of 50, denoted as \( \sqrt{50} \), is an important mathematical concept that provides insight into the properties of irrational numbers.

Firstly, let's express \( \sqrt{50} \) in its simplified form:

\[
\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}
\]

Since \( \sqrt{2} \) is known to be an irrational number, the product of a rational number (5) and an irrational number (\( \sqrt{2} \)) is also irrational. Therefore, \( \sqrt{50} \) is irrational.

The decimal representation of \( \sqrt{50} \) is approximately 7.071067811865475, which continues infinitely without repeating, further confirming its irrational nature.

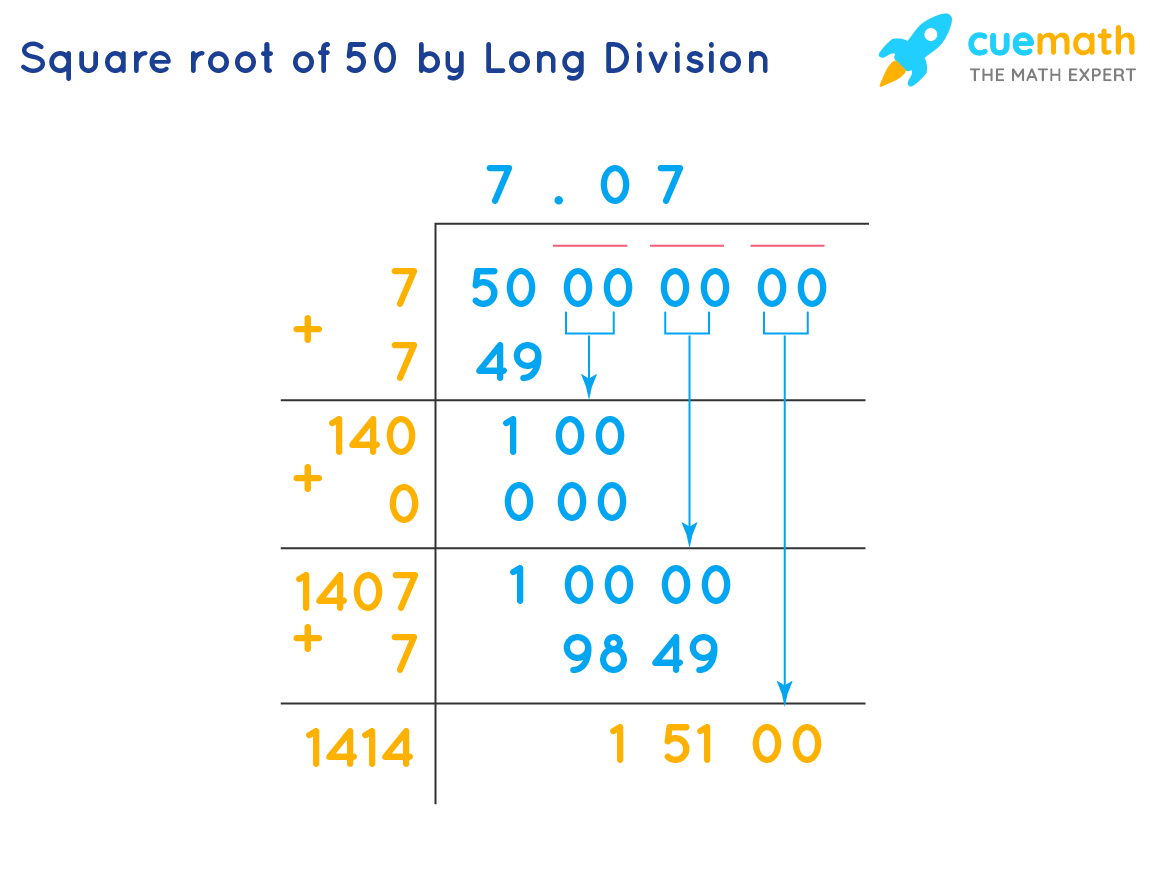
Several methods can be used to find the square root of 50:

• Prime Factorization Method: By breaking down 50 into its prime factors (2 and 5), we can simplify the square root.
• Long Division Method: This iterative method provides a precise value for \( \sqrt{50} \).
• Estimation Method: By recognizing that 50 lies between 49 (7²) and 64 (8²), we can estimate \( \sqrt{50} \) to be slightly more than 7.

Moreover, the historical significance and real-life applications of irrational numbers highlight their importance in various fields such as engineering, physics, and finance.

In conclusion, the square root of 50 exemplifies the properties of irrational numbers and their role in mathematics. Understanding and calculating such values enhance our comprehension of numerical relationships and their practical applications.