Topic how do you find the square root of 50: Discover how to find the square root of 50 using various methods, including prime factorization, long division, and approximation techniques. This guide simplifies the process, making it easy for you to understand and apply in practical scenarios. Learn the best approaches to calculate and visualize the square root of 50 accurately.
Table of Content
- How to Find the Square Root of 50
- Introduction to Square Roots
- Understanding the Concept of Square Roots
- Methods to Calculate the Square Root of 50
- Approximation and Estimation Techniques
- Using a Calculator for Square Roots
- Visualizing the Square Root of 50
- Decimal Representation of √50
- Applications of Square Roots in Real Life
- Square Root Table for Quick Reference
- Common Questions and Misconceptions
- Conclusion and Key Takeaways
- YOUTUBE:
How to Find the Square Root of 50
Finding the square root of 50 can be approached using different methods. Below, we explore the prime factorization method, the long division method, and the approximation method. Each method provides a clear pathway to calculating or understanding the square root of 50.
Prime Factorization Method
This method involves breaking down the number into its prime factors.
- Find the prime factors of 50: \(50 = 2 \times 5^2\).
- Express the square root using these factors: .
- Simplify to get: \( \sqrt{50} = 5 \sqrt{2} \approx 7.071 \).
Long Division Method
The long division method allows for a step-by-step approach to finding the square root. Follow these steps:
- Pair the digits of the number from right to left. For 50, it becomes \(\overline{50}\).
- Find the largest number whose square is less than or equal to the leading digit(s). Here, it's 7 because \(7^2 = 49\).
- Subtract \(49\) from \(50\) to get \(1\), then bring down two zeros to make \(100\).
- Double the quotient (7), and use it as the next divisor's first digit (14X). Find the value of X such that \(14X \times X \leq 100\). Here, X is 0.
- Continue the process to get a more precise decimal approximation.
Using this method, the square root of 50 is approximately \( \sqrt{50} \approx 7.071 \).
Approximation Method
Another quick way to estimate the square root is by comparing it to known squares:
- The square root of 49 is 7.
- The square root of 64 is 8.
- Since 50 is closer to 49, the square root of 50 is slightly greater than 7.
- By approximation, \( \sqrt{50} \approx 7.071 \).
Visualization Using a Calculator
Using a calculator or software, you can quickly find the square root of 50 by entering it directly:
- Enter "50" into the calculator.
- Press the square root (√) button.
- The calculator displays \( \sqrt{50} \approx 7.0710678 \).
The exact value is an irrational number but for practical purposes, we use its decimal approximation \( 7.071 \).
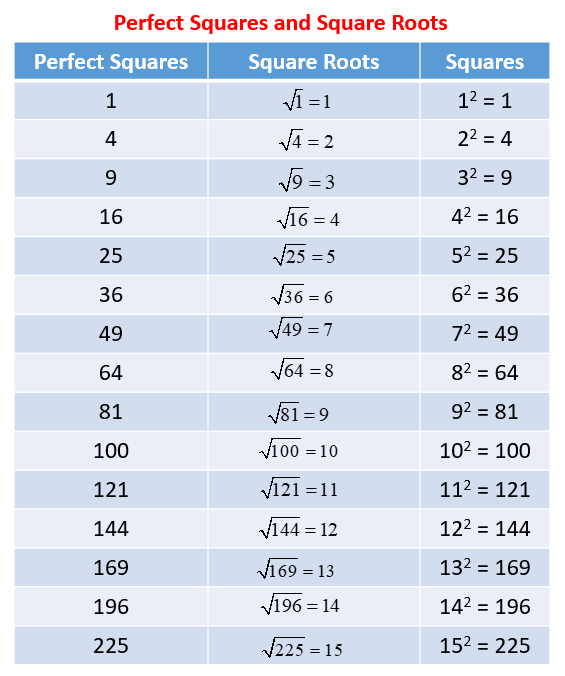
Square Root Table
| Number | Square Root |
|---|---|
| 49 | 7 |
| 50 | 7.071 |
| 51 | 7.141 |
READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics, offering a way to understand the properties of numbers. The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5 because \(5 \times 5 = 25\). Square roots are widely used in various fields, including algebra, geometry, and even real-life applications.
Mathematically, the square root of a number \( x \) is denoted as \( \sqrt{x} \). For positive numbers, the square root has both a positive and a negative value, though the principal (positive) root is typically used. Let's explore this concept with the example of finding the square root of 50.
- Definition: The square root of a number \( x \) is a value \( y \) such that \( y^2 = x \).
- Symbol: The square root symbol \( \sqrt{} \) is used to denote the operation.
- Principal Square Root: The positive value of the square root is known as the principal square root.
Understanding how to calculate the square root of non-perfect squares, like 50, involves different methods. These methods can help simplify complex problems and are essential in various mathematical applications.
- Prime Factorization: Breaking down the number into its prime factors.
- Long Division Method: A step-by-step approach to finding the square root to a desired decimal place.
- Approximation Techniques: Estimating the square root based on known values and patterns.
In the following sections, we will delve into each method to find the square root of 50 and see how these approaches can be applied practically. By the end of this guide, you'll have a comprehensive understanding of how to tackle square roots with confidence.
Understanding the Concept of Square Roots
The square root of a number is a foundational concept in mathematics, offering a way to understand how numbers relate to each other through their multiplicative properties. The square root of a number \( x \) is a value \( y \) such that \( y \times y = x \). This can also be expressed as \( y^2 = x \). For instance, since \( 7 \times 7 = 49 \), the square root of 49 is 7.
To grasp the concept of square roots more deeply, consider the following aspects:
- Square and Square Root Relationship: If \( y \) is the square root of \( x \), then \( y \times y = x \). Conversely, \( x \) is the square of \( y \). For example, since \( 6 \times 6 = 36 \), 6 is the square root of 36, and 36 is the square of 6.
- Principal and Negative Roots: Every positive number has two square roots: a positive root and a negative root. For example, the square roots of 25 are \( +5 \) and \( -5 \) because \( (+5) \times (+5) = 25 \) and \( (-5) \times (-5) = 25 \). The principal root refers to the positive square root.
- Irrational Numbers: Some numbers, like 50, do not have an exact square root in the set of rational numbers. Instead, their square roots are irrational numbers, which cannot be expressed as a simple fraction. The square root of 50, for instance, is approximately 7.071, which continues infinitely without repeating.
To calculate the square root of 50, you might use several methods:
- Prime Factorization: This involves breaking down the number into its prime factors and simplifying. For 50, this is \( 2 \times 5^2 \), leading to \( \sqrt{50} = \sqrt{2 \times 25} = 5\sqrt{2} \).
- Long Division Method: A step-by-step procedure to find the decimal value of the square root. This method helps you find precise values for square roots of non-perfect squares.
- Estimation and Approximation: This method involves using nearby perfect squares to estimate the value. Since 50 is close to 49, whose square root is 7, we can approximate \( \sqrt{50} \) to be slightly greater than 7.
Understanding square roots also involves visualizing them. Consider a square with an area of 50 square units. The side length of this square is the square root of 50. This geometric interpretation helps in visualizing and understanding the concept beyond numerical calculations.
| Number | Square Root |
|---|---|
| 36 | 6 |
| 49 | 7 |
| 50 | 7.071 |
| 64 | 8 |
By exploring these methods and concepts, you will gain a solid understanding of square roots and how to calculate them, even for complex numbers like 50.
Methods to Calculate the Square Root of 50
Calculating the square root of 50 can be approached using various methods, each with its own steps and advantages. Here, we will explore the Prime Factorization Method, the Long Division Method, and Approximation Techniques. These methods will help you find accurate values for the square root of 50, whether for quick estimation or precise calculation.
Prime Factorization Method
This method involves breaking down the number into its prime factors and simplifying the square root expression.
- Start by finding the prime factors of 50:
- 50 can be written as \( 50 = 2 \times 5^2 \).
- Express the square root using these factors: .
- Simplify to get the final result: .
Long Division Method
This method provides a step-by-step approach to calculate the square root of a number to a desired level of precision.
- Pair the digits of the number from right to left. For 50, it becomes \(\overline{50}\).
- Find the largest number whose square is less than or equal to the leading digit(s). In this case, it's 7 because \( 7^2 = 49 \).
- Subtract 49 from 50 to get 1. Bring down a pair of zeros to get 100.
- Double the quotient (7), and use it as the first part of the next divisor (14X). Determine the value of X so that \( 14X \times X \leq 100 \). Here, X is 0, so we bring down another pair of zeros to make 10000.
- Repeat the process to achieve a more precise value. For example:
7.071 \(7.071 \times 7.071 = 49.999041\)
Approximation Techniques
When a quick estimate is needed, approximation methods are useful:
- Between Two Perfect Squares: Identify two perfect squares between which 50 lies. Since \( \sqrt{49} = 7 \) and \( \sqrt{64} = 8 \), we know \( \sqrt{50} \) is slightly greater than 7.
- Average Method: Average the two closest integers' squares:
- Take the average of 7 and 8: \( \frac{7 + 8}{2} = 7.5 \).
- Square 7.5: \( 7.5 \times 7.5 = 56.25 \). Since 56.25 is greater than 50, try a smaller number like 7.1.
- Refine the Estimate: Continue refining until you approach the actual square root. For example, 7.07 is a closer approximation.
Using these methods, you can find that the square root of 50 is approximately \( \sqrt{50} \approx 7.071 \). Whether you need a precise value or a quick estimate, these techniques provide reliable ways to calculate square roots.
Approximation and Estimation Techniques
When exact calculations are not necessary or when dealing with complex numbers, approximation and estimation techniques for finding square roots can be extremely useful. These methods are particularly helpful for quickly estimating the square root of non-perfect squares like 50. Here are some common techniques to approximate the square root of 50:
Method 1: Using Nearby Perfect Squares
This method involves finding perfect squares close to the number in question and using them to estimate the square root.
- Identify the perfect squares surrounding 50. In this case:
- \( 49 = 7^2 \)
- \( 64 = 8^2 \)
- Since 50 lies between 49 and 64, its square root lies between 7 and 8.
- Estimate that \( \sqrt{50} \) is slightly more than 7 but less than 8. A closer estimate would be around 7.1 because \( 7.1 \times 7.1 = 50.41 \), which is close to 50.
Method 2: Average Method
The Average Method refines the estimation by averaging the results of successive approximations.
- Start with the closest integers, 7 and 8, because \( 49 < 50 < 64 \).
- Calculate the average: .
- Square the average to check accuracy: .
- Since 56.25 is larger than 50, we know that \( \sqrt{50} \) is less than 7.5. Try a smaller average, such as 7.2:
- \( \frac{7 + 7.5}{2} = 7.25 \)
- Square 7.25 to refine: \( 7.25 \times 7.25 = 52.5625 \)
- Continue refining until you get closer to 50. For example, \( 7.07 \times 7.07 = 49.9849 \), which is very close to 50.
Method 3: Newton's Method (or Heron's Method)
This iterative method involves a formula to refine estimates and converge on the accurate square root.
- Start with an initial guess (e.g., 7 for \( \sqrt{50} \)).
- Apply the formula: .
- Calculate the next approximation:
- For \( x_0 = 7 \): .
- Continue iterating until the change between successive approximations is minimal. After a few iterations, you will find that \( x \approx 7.071 \).
Each of these methods provides a way to estimate the square root of 50 effectively. Depending on the required precision and available tools, you can choose the method that best suits your needs.

Using a Calculator for Square Roots
Calculating the square root of 50 using a calculator is straightforward and efficient. Follow these steps to find the square root accurately:
- Turn on your calculator: Ensure your calculator is powered on and functional. For most scientific and graphing calculators, this is done by pressing the power button.
- Locate the square root function: Look for the square root button, typically represented by the radical symbol (√) or labeled as "sqrt." This button is usually found on scientific calculators and graphing calculators. If you are using a basic calculator without this function, refer to its manual for alternative methods like using exponentiation.
- Enter the number: Input the number 50 into the calculator. This is done by pressing the digits '5' and '0' sequentially.
- Execute the square root function: After entering the number 50, press the square root button (√). The calculator will compute the square root of 50.
- Interpret the result: The calculator will display the square root of 50, which is approximately 7.071. This result can be rounded to the desired number of decimal places as needed.
Using a calculator to find square roots is quick and minimizes errors, making it ideal for academic and professional applications.
Visualizing the Square Root of 50
Visualizing the square root of 50 can help in understanding its value and properties. Here are some methods to visualize and conceptualize the square root of 50:
Graphical Representation
One way to visualize √50 is to plot it on a number line. Since 72 = 49 and 82 = 64, √50 is between 7 and 8. More precisely, it is approximately 7.071. You can mark this point on the number line to get a sense of its position relative to whole numbers.
Additionally, if you plot the function y = √x, you can see how the curve progresses and where x = 50 falls on this curve.
Square Area Representation
Visualizing the square root of a number can also be done by considering the area of a square. For instance, the square root of 50 can be seen as the length of the side of a square with an area of 50 square units. Since 72 = 49 and 82 = 64, we know that a square with an area of 50 square units will have a side length between 7 and 8 units.
Prime Factorization Visualization
Using prime factorization, we can express 50 as:
\[ 50 = 2 \times 5^2 \]
Taking the square root of both sides gives us:
\[ \sqrt{50} = \sqrt{2 \times 5^2} = 5 \sqrt{2} \]
Since \(\sqrt{2} \approx 1.414\), we get:
\[ \sqrt{50} \approx 5 \times 1.414 = 7.07 \]
Geometric Representation
Another approach is to use a geometric method. Imagine a right triangle where the legs are of length 5 and 5√2. The hypotenuse of this triangle will then be √(52 + (5√2)2) = √50. This helps in visualizing √50 as the diagonal of a rectangle with sides 5 and 5√2.
Decimal Approximation
For practical purposes, knowing the decimal approximation is useful. We find that:
\[ \sqrt{50} \approx 7.0710678 \]
This can be visualized by noting that it is a non-terminating, non-repeating decimal, characteristic of irrational numbers.
Visualization Using a Grid
If you create a grid of 50 unit squares, arranging them into as close to a square shape as possible, you'll notice that the side length of this nearly square grid is around 7.071 units.
Overall, these visual and graphical methods can help in comprehending the square root of 50 beyond its numerical value.
Decimal Representation of √50
The square root of 50 is an irrational number, meaning its decimal representation is non-terminating and non-repeating. The decimal value of √50 can be approximated through various methods. Here, we will explore some of these methods in detail.
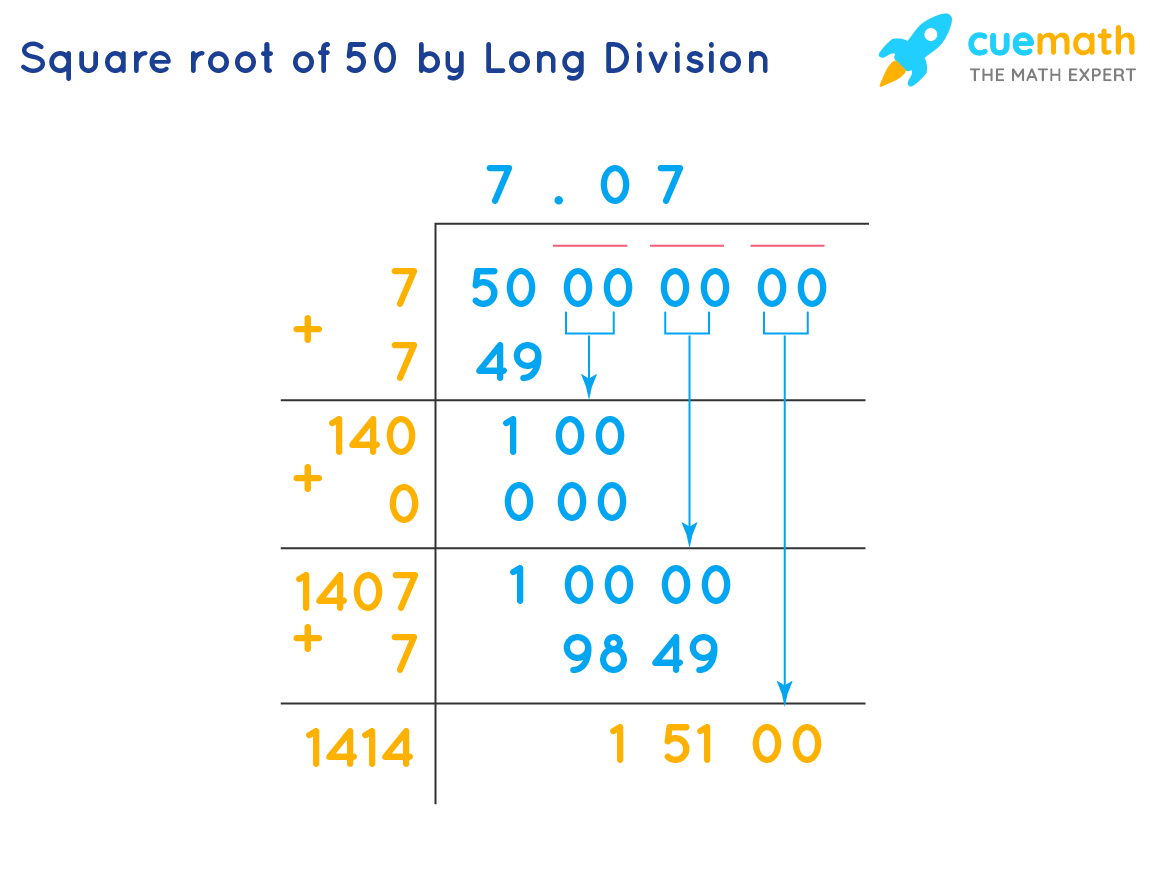
Using the Long Division Method
- Begin by writing 50 followed by pairs of zeros (e.g., 50.000000).
- Group the digits in pairs starting from the decimal point and moving left and right (e.g., 50, 00, 00, 00).
- Find a number (7) such that when multiplied by itself, the product is less than or equal to 50. \(7 \times 7 = 49\). Place 7 as the first digit of the quotient.
- Subtract 49 from 50 to get the remainder 1. Bring down the next pair of zeros to get 100.
- Double the quotient (7) to get 14. Determine a digit (0) to add to 14 to make a new divisor (140) which, when multiplied by the new digit, gives a product less than or equal to 100. The quotient is now 7.0.
- Repeat the process: bring down the next pair of zeros to get 10000, adjust the divisor (1400), and find the next digit (7). The quotient is now 7.07.
- Continue this process to get a more precise value. For example, 7.0710678...
Prime Factorization Method
- Express 50 as the product of prime factors: \(50 = 2 \times 5^2\).
- Taking the square root of both sides: \(\sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2}\).
- Since \(\sqrt{2} \approx 1.414\), we get \(5 \times 1.414 \approx 7.07\).
Decimal Approximation
Through repeated iterations, it is found that the square root of 50 is approximately \(7.0710678\). This value is useful in various practical applications and calculations where an exact root is not necessary.
Visual Representation
To visualize \(\sqrt{50}\), plot it on a number line between the integers 7 and 8, closer to 7. Alternatively, consider a square with an area of 50 square units; the side length of this square is \(\sqrt{50} \approx 7.071\) units.
Applications of Square Roots in Real Life
Square roots are used in various real-life applications across different fields. Here are some notable examples:
-
Finance:
In finance, square roots are used to calculate stock market volatility. The volatility is determined by taking the square root of the variance of a stock's returns. This helps investors assess the risk associated with their investments.
-
Architecture and Engineering:
Engineers use square roots to determine the natural frequencies of structures such as bridges and buildings. This helps in predicting how structures will respond to different forces like wind or traffic, ensuring safety and stability.
-
Science:
Square roots are essential in various scientific calculations, including determining the velocity of moving objects, the amount of radiation absorbed by materials, and the intensity of sound waves. These calculations are fundamental in understanding natural phenomena and developing new technologies.
-
Statistics:
In statistics, square roots are used to calculate standard deviation, which is the square root of the variance. This measure indicates how much data deviates from the mean, helping statisticians analyze data sets effectively.
-
Geometry:
In geometry, square roots are used to find the length of the sides of right triangles (Pythagorean theorem), and to calculate areas and perimeters of various shapes. This is crucial for solving many geometric problems.
-
Computer Science:
Square roots are utilized in computer programming for encryption algorithms, image processing, and game physics. For example, encryption algorithms use square roots to generate secure keys for data transmission.
-
Navigation:
In navigation, square roots help calculate the distance between two points on a map or globe, aiding in route planning and travel estimations. Pilots and sailors use these calculations for accurate navigation.
-
Electrical Engineering:
Square roots are applied to compute power, voltage, and current in electrical circuits. These calculations are fundamental in designing and developing electrical systems, including power grids and electronic devices.
-
Photography:
The aperture of a camera lens, which controls the amount of light entering the camera, is related to the square root. Adjusting the f-number (aperture size) changes the light entering the camera proportionally, affecting image exposure.
-
Cooking:
When scaling recipes, square roots can help maintain the right balance of ingredients. For instance, if you double a recipe, you might need to adjust the amount of spices by using the square root of the scaling factor.

Square Root Table for Quick Reference
The table below provides a quick reference for the square roots of numbers from 1 to 50. This can be particularly useful for solving mathematical problems quickly and efficiently. Each entry in the table shows the number and its corresponding square root.
| Number | Square Root (√) | Number | Square Root (√) | Number | Square Root (√) |
|---|---|---|---|---|---|
| 1 | 1.000 | 18 | 4.243 | 35 | 5.916 |
| 2 | 1.414 | 19 | 4.359 | 36 | 6.000 |
| 3 | 1.732 | 20 | 4.472 | 37 | 6.083 |
| 4 | 2.000 | 21 | 4.583 | 38 | 6.164 |
| 5 | 2.236 | 22 | 4.690 | 39 | 6.245 |
| 6 | 2.449 | 23 | 4.796 | 40 | 6.325 |
| 7 | 2.646 | 24 | 4.899 | 41 | 6.403 |
| 8 | 2.828 | 25 | 5.000 | 42 | 6.481 |
| 9 | 3.000 | 26 | 5.099 | 43 | 6.557 |
| 10 | 3.162 | 27 | 5.196 | 44 | 6.633 |
| 11 | 3.317 | 28 | 5.292 | 45 | 6.708 |
| 12 | 3.464 | 29 | 5.385 | 46 | 6.782 |
| 13 | 3.606 | 30 | 5.477 | 47 | 6.856 |
| 14 | 3.742 | 31 | 5.568 | 48 | 6.928 |
| 15 | 3.873 | 32 | 5.657 | 49 | 7.000 |
| 16 | 4.000 | 33 | 5.745 | 50 | 7.071 |
| 17 | 4.123 | 34 | 5.831 |
This table shows the square roots for numbers from 1 to 50, making it easy to find the square root of any number in this range at a glance.
Common Questions and Misconceptions
Understanding square roots can sometimes be challenging due to various common questions and misconceptions. Below, we address some of the most frequently asked questions and clarify misunderstandings.
-
Is the square root of a number always positive?
Yes, by definition, the square root function returns the non-negative root. For example, \(\sqrt{25} = 5\), not \(\pm 5\). This is because the square root function is defined to be the principal (non-negative) square root to ensure it is a function.
-
Can the square root of a negative number be real?
No, the square root of a negative number is not a real number; it is an imaginary number. For example, \(\sqrt{-25} = 5i\), where \(i\) is the imaginary unit (\(i = \sqrt{-1}\)).
-
Does every number have a square root?
Yes, every number has a square root. Positive numbers have two square roots (one positive and one negative), zero has one square root (itself), and negative numbers have two imaginary roots.
-
Can square roots be rational numbers?
Yes, the square roots can be rational numbers if the number under the square root is a perfect square. For example, \(\sqrt{16} = 4\), which is a rational number. However, \(\sqrt{50}\) is irrational because 50 is not a perfect square.
-
Are square roots always integers?
No, square roots are not always integers. Only perfect squares have integer square roots. For example, \(\sqrt{81} = 9\) is an integer, but \(\sqrt{50}\) is approximately 7.071, which is not an integer.
-
Can you add square roots?
Square roots can be added if they are like terms. For example, \(\sqrt{2} + \sqrt{2} = 2\sqrt{2}\). However, \(\sqrt{2} + \sqrt{3}\) cannot be simplified further because they are not like terms.
By understanding these common questions and misconceptions, we can better grasp the concept of square roots and their properties.
Conclusion and Key Takeaways
Understanding how to find and simplify the square root of 50 offers valuable insights into mathematical concepts and their practical applications. Here are the key takeaways:
- Square Root Basics: The square root of a number is a value that, when multiplied by itself, gives the original number. For 50, the square root is approximately 7.071.
- Methods of Calculation: There are multiple ways to calculate the square root of 50, including prime factorization and long division. The prime factorization method simplifies √50 to 5√2.
- Decimal Representation: The square root of 50 in decimal form is 7.071067811865475. This representation is useful in various scientific and engineering calculations.
- Visual Representation: Visualizing the square root of 50 can be done using number lines or geometric interpretations, helping to grasp the concept more intuitively.
- Applications: Square roots are used in numerous real-life scenarios, such as physics, engineering, and computer science, where precise calculations are crucial.
- Misconceptions: Common misconceptions include assuming the square root of a number is always an integer or rational number. The square root of 50, being an irrational number, demonstrates the complexity of square roots.
- Practical Tools: Calculators and software tools can quickly and accurately compute square roots, making complex calculations more manageable.
In summary, mastering the methods to calculate and understand square roots, such as that of 50, is essential for both academic purposes and practical applications in various fields.
Cách Đơn Giản Hóa Căn Bậc Hai của 50: Sqrt(50)
READ MORE:
Căn Bậc Hai Của 50 (Giải Thích)