Topic square root questions: Discover the essential guide to mastering square root questions with ease and confidence. This comprehensive article covers everything you need to know about square roots, from basic concepts to advanced problem-solving techniques. Enhance your math skills and conquer square root challenges with practical tips, examples, and practice problems. Start your journey to becoming a square root expert today!
Table of Content
- Square Root Questions
- Introduction to Square Roots
- Understanding the Concept of Square Roots
- Properties of Square Roots
- Methods to Calculate Square Roots
- Square Root of Perfect Squares
- Square Root of Non-Perfect Squares
- Square Roots and Real Numbers
- Simplifying Square Roots
- Square Root Applications in Real Life
- Solving Square Root Equations
- Graphing Square Root Functions
- Common Mistakes and How to Avoid Them
- Square Roots in Geometry
- Square Roots and Pythagorean Theorem
- Square Roots in Algebra
- Square Roots and Exponents
- Using Square Root Tables
- Square Roots and Scientific Calculations
- YOUTUBE: Video hướng dẫn cách đơn giản hóa căn bậc hai bằng các phương pháp dễ hiểu và hiệu quả.
Square Root Questions
Here is a synthesis of information regarding square root questions:
1. What is a Square Root?
The square root of a number is a value that, when multiplied by itself, gives the original number.
2. Types of Square Root Questions
Common types of square root questions include:
- Finding the square root of a perfect square number.
- Estimating the square root of a non-perfect square number.
- Solving equations involving square roots.
- Applications in geometry, physics, and engineering.
3. Methods for Finding Square Roots
Methods to find square roots include:
- Guess and check method.
- Prime factorization method.
- Using a calculator or computer program.
- Using numerical methods like Newton's method.
4. Important Concepts Related to Square Roots
Key concepts include:
- The principal square root.
- Radical notation and simplification rules.
- The relationship between squares and square roots.
- Real and complex square roots.
5. Resources for Learning More
For further exploration, consider resources such as:
- Online tutorials and courses.
- Mathematics textbooks and reference books.
- Interactive websites and apps.
- Mathematics forums and communities.

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is represented using the radical symbol √. For example, the square root of 9 is 3, since \( 3 \times 3 = 9 \).
Here are some basic properties and concepts related to square roots:
- The square root of a positive number has two values: a positive and a negative root. For example, the square root of 16 is ±4.
- The square root of 0 is 0.
- Negative numbers do not have real square roots. Their square roots are imaginary numbers.
To understand square roots better, let's explore some key points step by step:
- Definition: The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \).
- Notation: The square root of \( x \) is denoted as \( \sqrt{x} \).
- Perfect Squares: Numbers like 1, 4, 9, 16, 25 are perfect squares because their square roots are integers.
- Non-Perfect Squares: Numbers like 2, 3, 5, 7 do not have integer square roots. Their square roots are irrational numbers.
Here is a table of some common square roots:
| Number | Square Root |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
Using the properties of square roots can simplify complex mathematical problems and help in various applications in algebra, geometry, and beyond. Understanding the fundamentals of square roots lays a solid foundation for more advanced mathematical concepts.
Understanding the Concept of Square Roots
The concept of square roots is fundamental in mathematics, providing a basis for understanding more complex algebraic and geometric principles. Let's break down the concept step by step.
A square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). In other words, if you square \( y \), you get \( x \).
Here are some important points to understand about square roots:
- Notation: The square root of \( x \) is denoted as \( \sqrt{x} \). For example, \( \sqrt{25} = 5 \).
- Positive and Negative Roots: Every positive number \( x \) has two square roots: \( +\sqrt{x} \) and \( -\sqrt{x} \). For instance, the square roots of 9 are 3 and -3 because \( 3^2 = 9 \) and \( (-3)^2 = 9 \).
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares. Their square roots are whole numbers.
- Non-Perfect Squares: Numbers that are not perfect squares, such as 2, 3, 5, and 7, have square roots that are irrational numbers (cannot be expressed as a simple fraction).
- Zero: The square root of 0 is 0 because \( 0 \times 0 = 0 \).
- Negative Numbers: Negative numbers do not have real square roots because there is no real number that, when squared, gives a negative number. Instead, they have imaginary square roots.
To deepen your understanding, let's consider some examples:
- Square Root of a Perfect Square:
- The square root of 16 is \( \sqrt{16} = 4 \) because \( 4 \times 4 = 16 \).
- The square root of 81 is \( \sqrt{81} = 9 \) because \( 9 \times 9 = 81 \).
- Square Root of a Non-Perfect Square:
- The square root of 2 is approximately \( \sqrt{2} \approx 1.414 \) because \( 1.414 \times 1.414 \approx 2 \).
- The square root of 3 is approximately \( \sqrt{3} \approx 1.732 \) because \( 1.732 \times 1.732 \approx 3 \).
Understanding square roots also involves recognizing how they interact with other mathematical operations:
- Multiplication and Division: \( \sqrt{a} \times \sqrt{b} = \sqrt{a \times b} \) and \( \sqrt{a} \div \sqrt{b} = \sqrt{a \div b} \).
- Square of a Square Root: \( (\sqrt{a})^2 = a \).
Here is a table of common square roots for quick reference:
| Number | Square Root |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
By mastering the concept of square roots, you can tackle a variety of mathematical problems with confidence and ease. Whether working with equations, graphs, or real-life applications, understanding square roots is an essential skill in mathematics.
Properties of Square Roots
The square root of a number has several important properties that are essential for understanding and solving mathematical problems. Here are some key properties:
- Non-negativity: For any real number \( x \), \( \sqrt{x} \) is always non-negative. This means \( \sqrt{x} \geq 0 \).
- Product Property: The square root of a product is equal to the product of the square roots. For any non-negative numbers \( a \) and \( b \): \[ \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \]
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots. For any non-negative numbers \( a \) and \( b \) where \( b \neq 0 \): \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
- Square of a Square Root: The square of a square root returns the original number. For any non-negative number \( x \): \[ (\sqrt{x})^2 = x \]
- Square Root of Zero: The square root of zero is zero: \[ \sqrt{0} = 0
- Square Root of One: The square root of one is one: \[ \sqrt{1} = 1 \]
- Square Root of a Square: For any real number \( x \), the square root of \( x^2 \) is the absolute value of \( x \): \[ \sqrt{x^2} = |x|
Below is a table summarizing these properties:
| Property | Mathematical Representation |
|---|---|
| Non-negativity | \(\sqrt{x} \geq 0\) |
| Product Property | \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\) |
| Quotient Property | \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) |
| Square of a Square Root | \((\sqrt{x})^2 = x\) |
| Square Root of Zero | \(\sqrt{0} = 0\) |
| Square Root of One | \(\sqrt{1} = 1\) |
| Square Root of a Square | \(\sqrt{x^2} = |x|\) |
These properties form the foundation for more advanced concepts and problem-solving techniques involving square roots.
Methods to Calculate Square Roots
Calculating square roots can be done through several methods, each with its own advantages. Here, we outline some of the most common methods:
1. Prime Factorization Method
This method is suitable for perfect squares. It involves breaking down the number into its prime factors and then pairing the factors to find the square root.
- Factor the number into its prime factors.
- Pair the prime factors.
- Take one factor from each pair and multiply them to get the square root.
Example:
Find the square root of 81:
- Prime factorization: \(81 = 3 \times 3 \times 3 \times 3\)
- Pair the factors: \((3 \times 3) \times (3 \times 3)\)
- Square root: \(3 \times 3 = 9\)
2. Long Division Method
This method works for both perfect and non-perfect squares. It's a systematic approach that can be used to find square roots up to the desired decimal places.
- Separate the number into pairs of digits starting from the decimal point.
- Find the largest number whose square is less than or equal to the first pair.
- Subtract this square from the first pair and bring down the next pair of digits.
- Double the quotient and find a digit that can be appended to the quotient and the divisor to form a new divisor.
- Repeat the process for the remaining pairs of digits.
Example:
Find the square root of 7921:
| Step | Operation | Result |
| 1 | Separate into pairs: 79 21 | |
| 2 | Find the largest number whose square ≤ 79: 8 | 8 |
| 3 | 8² = 64, 79 - 64 = 15, bring down 21 | 1521 |
| 4 | Double the quotient: 2 × 8 = 16, find the next digit | 162 |
| 5 | 162 × 9 = 1458, 1521 - 1458 = 63 | |
| 6 | Result: √7921 = 89 | 89 |
3. Newton's Method (Heron's Method)
This iterative method is efficient for finding square roots, especially when a high degree of precision is required.
- Start with an initial guess \(x_0\).
- Use the formula \(x_{n+1} = \frac{1}{2}\left( x_n + \frac{S}{x_n} \right)\) to find the next approximation.
- Repeat the process until the difference between \(x_n\) and \(x_{n+1}\) is smaller than the desired precision.
Example:
Find the square root of 10 using Newton's method:
- Initial guess: \(x_0 = 3\)
- First iteration: \(x_1 = \frac{1}{2} \left( 3 + \frac{10}{3} \right) = 3.1667\)
- Second iteration: \(x_2 = \frac{1}{2} \left( 3.1667 + \frac{10}{3.1667} \right) = 3.1623\)
- Result: \(√10 ≈ 3.1623\)
4. Estimation and Refinement
This method involves estimating the square root by finding two consecutive perfect squares between which the number lies and then refining the estimate using averages.
- Identify two consecutive perfect squares between which the number lies.
- Divide the number by one of these roots and find the average of the result and the root.
- Use the average as a new estimate and repeat the process.
Example:
Find the square root of 10:
- Estimate: \(3^2 = 9\) and \(4^2 = 16\), so \(√10\) lies between 3 and 4.
- Divide and average: \(\frac{10}{3} = 3.33\), average: \(\frac{3 + 3.33}{2} = 3.1667\).
- Repeat: \(\frac{10}{3.1667} = 3.1579\), average: \(\frac{3.1667 + 3.1579}{2} = 3.1623\).
- Result: \(√10 ≈ 3.1623\)

Square Root of Perfect Squares
Perfect squares are numbers that are the product of an integer multiplied by itself. For example, the numbers 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100 are all perfect squares. The square root of a perfect square is always an integer.
Examples of Perfect Squares
- \(1 = 1^2 \Rightarrow \sqrt{1} = 1\)
- \(4 = 2^2 \Rightarrow \sqrt{4} = 2\)
- \(9 = 3^2 \Rightarrow \sqrt{9} = 3\)
- \(16 = 4^2 \Rightarrow \sqrt{16} = 4\)
- \(25 = 5^2 \Rightarrow \sqrt{25} = 5\)
- \(36 = 6^2 \Rightarrow \sqrt{36} = 6\)
- \(49 = 7^2 \Rightarrow \sqrt{49} = 7\)
- \(64 = 8^2 \Rightarrow \sqrt{64} = 8\)
- \(81 = 9^2 \Rightarrow \sqrt{81} = 9\)
- \(100 = 10^2 \Rightarrow \sqrt{100} = 10\)
Properties of Perfect Squares
Perfect squares have specific properties that make them unique:
- Integer Roots: The square root of a perfect square is always an integer.
- Positive and Negative Roots: Every perfect square has two square roots: one positive and one negative. For example, \( \sqrt{25} = 5 \) and \( \sqrt{25} = -5 \).
- Non-negative: Perfect squares are always non-negative since the product of any real number with itself is non-negative.
How to Identify Perfect Squares
To identify if a number is a perfect square, determine if there exists an integer \( n \) such that \( n^2 = \) the given number. For instance:
- Is 49 a perfect square? \( 7^2 = 49 \). Therefore, 49 is a perfect square.
- Is 50 a perfect square? There is no integer \( n \) such that \( n^2 = 50 \). Therefore, 50 is not a perfect square.
Applications of Perfect Squares
Perfect squares are used in various mathematical contexts, including algebra, geometry, and real-world applications:
- Geometry: Perfect squares are used in calculating areas of squares and in the Pythagorean theorem.
- Algebra: Simplifying expressions and solving quadratic equations often involve recognizing perfect squares.
- Everyday Use: Perfect squares appear in real-life situations such as determining dimensions in construction and design.
Practice Problems
- Find the square root of 144.
- Is 121 a perfect square? If so, find its square root.
- Simplify the expression \( \sqrt{225} \).
- Determine if 200 is a perfect square.
Square Root of Non-Perfect Squares
Calculating the square root of non-perfect squares can be more complex than finding the square root of perfect squares. Non-perfect squares are numbers that do not result in an integer when their square root is taken. Below are several methods to approximate these square roots:
1. Estimation Method
This method involves finding the two closest perfect squares between which the non-perfect square lies.
- Identify the perfect squares closest to the given number. For example, to find √90, the nearest perfect squares are 81 (9²) and 100 (10²).
- Determine that the square root of 90 falls between 9 and 10.
- Make an initial guess (e.g., 9.5) and refine it. Calculate 9.5² = 90.25, which is close but slightly above 90. Adjust the guess to 9.45 and calculate again.
Continue adjusting until you get a satisfactory approximation.
2. Long Division Method
This method is more precise and involves the following steps:
- Start by grouping the digits of the number in pairs from the decimal point. For 90, write it as 90.00 to create pairs (90) (00).
- Find the largest number whose square is less than or equal to the first group. For 90, the closest perfect square is 81 (9²), so 9 is the first digit of the root.
- Subtract the square of this digit (81) from the first group (90), giving 9. Bring down the next pair of zeros, making it 900.
- Double the current quotient (9) to get 18, and find a digit x such that 18x × x is less than or equal to 900. The appropriate digit is 4, as 184 × 4 = 736.
- Repeat this process to get the next decimal places.
The result is an increasingly accurate approximation.
3. Iterative Method (Newton's Method)
This iterative method provides a more mathematical approach:
- Start with an initial guess \( x_0 \). For √90, a reasonable guess might be 9.
- Use the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{90}{x_n} \right) \) to find the next approximation.
- Continue iterating until the difference between successive approximations is sufficiently small.
For example, using Newton's method:
- Initial guess \( x_0 = 9 \)
- First iteration \( x_1 = \frac{1}{2} \left( 9 + \frac{90}{9} \right) = 9.5 \)
- Second iteration \( x_2 = \frac{1}{2} \left( 9.5 + \frac{90}{9.5} \right) \approx 9.487 \)
Examples and Practice
Practice these methods with different non-perfect squares to become proficient. Try finding the square roots of numbers like 2, 50, or 75 using each method to see which one works best for you.
Square Roots and Real Numbers
In mathematics, square roots are an essential part of understanding real numbers. Here, we explore how square roots relate to the set of real numbers.
The set of real numbers, denoted by \(\mathbb{R}\), includes all rational and irrational numbers. The square root function, denoted by \(\sqrt{x}\), is defined for non-negative real numbers \(x \geq 0\).
Key points about square roots and real numbers:
- For \(x \geq 0\), \(\sqrt{x}\) is the non-negative number \(y\) such that \(y^2 = x\).
- The square root function maps each non-negative real number to its principal (non-negative) square root.
- Examples of square roots of real numbers include:
- \(\sqrt{0} = 0\)
- \(\sqrt{1} = 1\)
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
- Square roots of non-perfect squares (irrational numbers) are irrational themselves, such as \(\sqrt{2}\) and \(\sqrt{5}\).
- Complex numbers are not included in the set of real numbers; they are typically considered in the context of the complex number set \(\mathbb{C}\).
Understanding square roots in relation to real numbers is fundamental in various mathematical disciplines, including algebra, geometry, and calculus.
Simplifying Square Roots
Square roots can often be simplified by factoring out perfect squares. Simplifying square roots helps in solving equations and understanding the properties of numbers. Here is a step-by-step guide to simplify square roots:
- Factor the number under the square root:
Break down the number under the square root into its prime factors.
Example: \( \sqrt{72} \) can be factored as \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
- Group the prime factors into pairs:
Identify and group pairs of the same number.
Example: \( \sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} \).
- Take out one number from each pair:
For each pair of prime factors, take one number out of the square root.
Example: \( \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2} \).
- Multiply the numbers outside the square root:
Combine the numbers taken out of the square root.
Example: \( 2 \times 3 = 6 \). Therefore, \( \sqrt{72} = 6\sqrt{2} \).
Examples of Simplified Square Roots
- \( \sqrt{18} = \sqrt{(3 \times 3) \times 2} = 3\sqrt{2} \)
- \( \sqrt{50} = \sqrt{(5 \times 5) \times 2} = 5\sqrt{2} \)
- \( \sqrt{98} = \sqrt{(7 \times 7) \times 2} = 7\sqrt{2} \)
Practice Problems
Try simplifying the following square roots:
- \( \sqrt{32} \)
- \( \sqrt{45} \)
- \( \sqrt{200} \)

Square Root Applications in Real Life
Square roots play a significant role in various real-life applications across different fields. Here are some key areas where square roots are commonly used:
1. Construction and Architecture
In construction, square roots are essential for calculating the lengths of diagonal braces to ensure the stability of structures. For example, when constructing a right-angled triangle with legs of known lengths, the length of the hypotenuse can be found using the Pythagorean theorem:
Using the formula: \( c = \sqrt{a^2 + b^2} \)
For a triangle with legs of 6 feet and 8 feet:
- \( a = 6 \)
- \( b = 8 \)
- \( c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \)
Thus, the length of the hypotenuse is 10 feet.
2. Finance
In finance, square roots are used to calculate stock market volatility, which involves determining the standard deviation of stock returns. This helps investors assess the risk associated with a particular investment.
The formula for standard deviation (\( \sigma \)) is:
\( \sigma = \sqrt{\frac{1}{N-1} \sum_{i=1}^{N} (R_i - \bar{R})^2} \)
Where \( N \) is the number of returns, \( R_i \) is each individual return, and \( \bar{R} \) is the mean return.
3. Science and Engineering
Square roots are used in various scientific calculations, such as determining the velocity of objects, calculating sound intensity, and measuring radiation levels.
For example, in physics, the distance \( D \) between two points in a 2D plane can be calculated using the distance formula, derived from the Pythagorean theorem:
\( D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
In a 3D space, the formula extends to:
\( D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \)
4. Computer Graphics and Game Development
In computer graphics, square roots are used to calculate distances between points, lengths of vectors, and for various transformations. These calculations are crucial for rendering images and animations accurately.
For instance, to find the length of a vector \( \mathbf{v} \) with components \( (x, y, z) \), the formula is:
\( |\mathbf{v}| = \sqrt{x^2 + y^2 + z^2} \)
5. Statistics
In statistics, square roots are used to calculate standard deviation, a measure of the dispersion of a set of values. It helps in understanding the spread and variability of data.
The standard deviation formula is:
\( \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2} \)
Where \( N \) is the number of data points, \( x_i \) is each data point, and \( \mu \) is the mean of the data.
6. Cryptography
In cryptography, square roots are used in algorithms for encryption and decryption processes, key exchanges, and digital signatures. These applications are fundamental for securing digital communications.
7. Navigation
In navigation, square roots are used to calculate the shortest distance between two points on a map, helping pilots and sailors to plot accurate courses.
Using the distance formula in a 2D plane, for points \((x_1, y_1)\) and \((x_2, y_2)\):
\( D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
These examples illustrate the importance of square roots in solving practical problems in everyday life and various professional fields.
Solving Square Root Equations
Solving square root equations involves isolating the square root expression and then squaring both sides of the equation to eliminate the square root. Here is a step-by-step guide to solving these types of equations:
- Isolate the Square Root
First, ensure the square root term is isolated on one side of the equation.
Example: Solve \( \sqrt{2x + 9} - 5 = 0 \)
- Isolate the square root: \( \sqrt{2x + 9} = 5 \)
- Square Both Sides
Next, square both sides of the equation to eliminate the square root.
- Square both sides: \( ( \sqrt{2x + 9} )^2 = 5^2 \)
- This simplifies to: \( 2x + 9 = 25 \)
- Solve the Resulting Equation
Continue solving the linear equation that results from the squaring step.
- Subtract 9 from both sides: \( 2x = 16 \)
- Divide by 2: \( x = 8 \)
- Check Your Solution
Substitute the solution back into the original equation to verify it does not result in a false statement.
- Check: \( \sqrt{2(8) + 9} - 5 = \sqrt{25} - 5 = 5 - 5 = 0 \)
Example with Two Square Roots
Sometimes equations involve more than one square root. Here is how to handle such cases:
Example: Solve \( \sqrt{2x - 5} - \sqrt{x - 1} = 1 \)
- Isolate one of the square roots:
\( \sqrt{2x - 5} = 1 + \sqrt{x - 1} \)
- Square both sides:
\( ( \sqrt{2x - 5} )^2 = (1 + \sqrt{x - 1})^2 \)
This simplifies to: \( 2x - 5 = 1 + 2\sqrt{x - 1} + (x - 1) \)
- Isolate the remaining square root:
\( 2x - 5 = x + 1 + 2\sqrt{x - 1} \)
Subtract \( x + 1 \) from both sides: \( x - 6 = 2\sqrt{x - 1} \)
- Square both sides again:
\( (x - 6)^2 = (2\sqrt{x - 1})^2 \)
This simplifies to: \( x^2 - 12x + 36 = 4(x - 1) \)
- Solve the resulting quadratic equation:
\( x^2 - 12x + 36 = 4x - 4 \)
Rearrange: \( x^2 - 16x + 40 = 0 \)
Solve using the quadratic formula: \( x = \frac{16 \pm \sqrt{16^2 - 4 \cdot 1 \cdot 40}}{2 \cdot 1} \)
This simplifies to: \( x = \frac{16 \pm \sqrt{256 - 160}}{2} \)
\( x = \frac{16 \pm \sqrt{96}}{2} \)
\( x = \frac{16 \pm 4\sqrt{6}}{2} \)
\( x = 8 \pm 2\sqrt{6} \)
- Check for extraneous solutions by substituting back into the original equation.
By following these steps and ensuring to check for extraneous solutions, you can solve square root equations accurately.
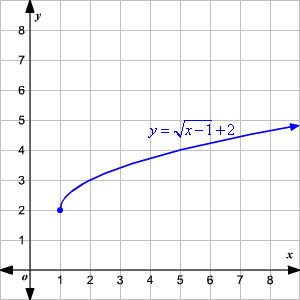
Graphing Square Root Functions
Graphing square root functions involves understanding their basic shape and properties. The most basic square root function is . Here is a step-by-step guide to graphing square root functions:
-
Identify the function: Let's start with the basic square root function: .
-
Create a table of values: Choose values of x and compute the corresponding values of f(x).
x f(x) = √x 0 0 1 1 4 2 9 3 16 4 -
Plot the points: Using the table of values, plot the points (0,0), (1,1), (4,2), (9,3), and (16,4) on a coordinate plane.
-
Draw the curve: Connect the plotted points with a smooth curve to illustrate the shape of the function. The curve should start at the origin (0,0) and increase slowly, getting steeper as x increases.
-
Understand the domain and range: The domain of is x ≥ 0, since square roots of negative numbers are not real. The range is f(x) ≥ 0.
-
Transformations: Consider transformations such as translations, reflections, and scaling. For example, shifts the graph 2 units to the right and 3 units up.
- Horizontal shifts: shifts the graph h units to the right.
- Vertical shifts: shifts the graph k units up.
- Reflections: reflects the graph across the x-axis.
- Vertical scaling: scales the graph vertically by a factor of a.
By following these steps, you can effectively graph any square root function and understand its behavior. Practice with different transformations to see how the graph changes.
Common Mistakes and How to Avoid Them
When working with square roots, students often make several common mistakes. Understanding these errors and learning how to avoid them can help improve mathematical accuracy and confidence.
-
Incorrectly Simplifying Square Roots: A common mistake is failing to properly simplify square roots.
- Mistake: Simplifying incorrectly as .
- Correction: Recognize that and simplify correctly: .
-
Adding and Subtracting Square Roots Incorrectly: Another frequent error is treating square roots like regular numbers when adding or subtracting.
- Mistake: Assuming .
- Correction: Understand that square roots must be added as . They cannot be combined under a single square root.
-
Misinterpreting the Square Root Symbol: Students often forget that the square root symbol represents the principal (non-negative) root.
- Mistake: Writing .
- Correction: Remember that . The symbol is used when solving equations like , giving solutions .
-
Forgetting to Check for Extraneous Solutions: When solving equations involving square roots, extraneous solutions can sometimes be introduced.
- Mistake: Not verifying solutions in the original equation.
- Correction: Always substitute solutions back into the original equation to confirm their validity.
-
Incorrectly Handling Square Roots of Negative Numbers: Square roots of negative numbers require special consideration involving imaginary numbers.
- Mistake: Ignoring the imaginary unit and incorrectly simplifying.
- Correction: Remember that . For example, .
-
Misapplying the Product and Quotient Rules: Misusing these rules can lead to incorrect results.
- Mistake: Incorrectly applying and without considering domain restrictions.
- Correction: Ensure that both a and b are non-negative before applying these rules. For example, and .
By recognizing these common mistakes and learning how to avoid them, you can improve your proficiency with square roots and solve problems more accurately.

Square Roots in Geometry
Square roots play a crucial role in geometry, particularly when dealing with areas and side lengths of squares and rectangles. Here’s how square roots are applied:
- Calculating Side Lengths: To find the side length of a square given its area, take the square root of the area. For example, if the area of a square is \( A \), then the side length \( s \) is \( s = \sqrt{A} \).
- Diagonal of a Square: The diagonal \( d \) of a square with side length \( s \) can be found using the formula \( d = s \sqrt{2} \).
- Rectangle Diagonal: For a rectangle with sides \( l \) (length) and \( w \) (width), the diagonal \( d \) is calculated as \( d = \sqrt{l^2 + w^2} \).
- Pythagorean Theorem: In right-angled triangles, square roots are used extensively through the Pythagorean Theorem, where \( c^2 = a^2 + b^2 \) and \( c \) represents the hypotenuse.
Understanding these principles helps in various geometric calculations, ensuring accurate measurements and relationships between shapes.
Square Roots and Pythagorean Theorem
The Pythagorean Theorem is a fundamental principle in geometry that relates to right-angled triangles. It states:
\[
c^2 = a^2 + b^2
\]
where \( c \) represents the length of the hypotenuse (the side opposite the right angle), and \( a \) and \( b \) represent the lengths of the other two sides.
Applying square roots in the context of the Pythagorean Theorem:
- Finding the Hypotenuse: Given the lengths of the two perpendicular sides \( a \) and \( b \), the length of the hypotenuse \( c \) is calculated using \( c = \sqrt{a^2 + b^2} \).
- Verification of Right Angles: To verify if a triangle is a right-angled triangle, you can check if \( a^2 + b^2 = c^2 \).
- Applications in Geometry: The Pythagorean Theorem is widely used in various geometric calculations, such as determining distances, dimensions, and angles in architectural designs, engineering, and surveying.
Square Roots in Algebra
In algebra, square roots are essential for solving equations involving squares and understanding relationships between variables. Here’s how square roots are used:
- Solving Quadratic Equations: To solve quadratic equations of the form \( ax^2 + bx + c = 0 \), square roots are used in the quadratic formula:
- Relationships between Variables: Square roots help in defining and understanding inverse relationships, such as square roots being the inverse operation of squaring a number or a variable.
- Applications in Factorization: Square roots aid in factorization, particularly when dealing with perfect squares and simplifying expressions.
- Geometric Mean: In algebraic contexts, the square root can be used to calculate the geometric mean of two numbers \( a \) and \( b \), defined as \( \sqrt{ab} \).
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Square Roots and Exponents
In mathematics, square roots and exponents are closely related, especially when dealing with powers and roots of numbers. Here’s how they interact:
- Square Roots as \( \frac{1}{2} \) Power: The square root of a number \( a \) can be expressed as \( a^{1/2} \).
- Exponentiation of Square Roots: Raising a square root to an exponent \( n \) results in \( \left(\sqrt{a}\right)^n = a^{n/2} \).
- Negative Exponents: Negative exponents in relation to square roots are managed through the reciprocal property, such as \( a^{-1/2} = \frac{1}{\sqrt{a}} \).
- Rational Exponents: Square roots are part of the broader concept of rational exponents, where \( a^{m/n} = \sqrt[n]{a^m} \).
Understanding these relationships helps in simplifying expressions involving roots and powers, providing insight into mathematical transformations and calculations.

Using Square Root Tables
Square root tables provide a convenient reference for quickly finding the square roots of numbers without using a calculator. Here’s how they are used:
Square root tables typically list numbers in the left column and their corresponding square roots in the right column.
| Number (\( x \)) | Square Root (\( \sqrt{x} \)) |
|---|---|
| 1 | 1.000 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2.000 |
| 5 | 2.236 |
| ... | ... |
Users can locate the number in the table and read off its square root directly, making it useful for educational purposes and applications where precise values are required.
Square Roots and Scientific Calculations
In scientific calculations, square roots are essential for various applications, especially in fields like physics, engineering, and chemistry. Here’s how they are utilized:
- Precision Measurements: Square roots are used to calculate precise measurements, such as determining the lengths of sides or dimensions of objects in experiments and designs.
- Root Mean Square (RMS) Values: In physics and electrical engineering, RMS values of alternating currents or voltages are calculated using square roots to determine effective values.
- Standard Deviation: Statistical calculations in research often involve square roots to find the standard deviation, which measures the amount of variation or dispersion in a set of data.
- Scientific Notation: Square roots help in simplifying and interpreting numbers in scientific notation, making large or small values more manageable and understandable.
- Natural Phenomena: Understanding natural phenomena, such as gravitational force or wave amplitudes, often requires calculations involving square roots to quantify and analyze data accurately.
By incorporating square roots into scientific calculations, researchers and scientists can derive meaningful insights and make informed decisions based on accurate data analysis.
Video hướng dẫn cách đơn giản hóa căn bậc hai bằng các phương pháp dễ hiểu và hiệu quả.
Cách Đơn Giản Hóa Căn Bậc Hai
READ MORE:
Tìm hiểu về khái niệm căn bậc hai với Mr. J trong video này. Khám phá cách tính toán và ứng dụng căn bậc hai một cách dễ hiểu và hấp dẫn.
Căn Bậc Hai Là Gì? | Toán Học Cùng Mr. J