Topic square root formula with example: Explore the intricacies of square roots with our comprehensive guide. From understanding the basic concept to advanced calculation methods and practical applications, this article covers everything you need to master square roots. Whether you're a student or enthusiast, dive into examples, properties, and tips to enhance your mathematical skills.
Table of Content
- Square Root Formula
- Introduction to Square Roots
- Understanding the Square Root Symbol
- Basic Concept of Square Roots
- Square Root Formula
- Methods to Calculate Square Roots
- Prime Factorization Method
- Long Division Method
- Using a Calculator to Find Square Roots
- Examples of Square Root Calculations
- Simple Square Root Examples
- Complex Square Root Examples
- Square Roots of Perfect Squares
- Square Roots of Non-Perfect Squares
- Applications of Square Roots
- Square Roots in Geometry
- Square Roots in Algebra
- Real-Life Applications of Square Roots
- Common Mistakes and Misconceptions
- YOUTUBE: Xem video để học cách tính căn bậc hai - một trong những con số đã thay đổi toán học mãi mãi.
Square Root Formula
The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). The square root formula is expressed as:
Example
Let's find the square root of 16:
- Given \( x = 16 \)
- We need to find \( y \) such that \( y^2 = 16 \)
- The value of \( y \) is 4, because \( 4^2 = 16 \)
Thus, the square root of 16 is 4.
Properties of Square Roots
- Non-negative Results: The square root of a non-negative number is always non-negative.
- Zero: The square root of 0 is 0.
- Product Property: The square root of a product is the product of the square roots.
- Quotient Property: The square root of a quotient is the quotient of the square roots.
Negative Numbers
Square roots of negative numbers are not real numbers. Instead, they are complex numbers. The square root of a negative number \( -x \) is represented as:
where \( i \) is the imaginary unit, defined by \( i^2 = -1 \).

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 9 is 3 because 3 multiplied by 3 equals 9. Square roots are fundamental in various branches of mathematics and have practical applications in fields such as engineering, physics, and computer science.
In mathematical notation, the square root of a number \( x \) is represented as \( \sqrt{x} \). The symbol \( \sqrt{} \) is known as the radical sign, and the number under the radical sign is called the radicand.
Here are some key points about square roots:
- The square root of a positive number is always a positive number.
- Every positive number has two square roots: one positive and one negative. For example, the square roots of 16 are 4 and -4.
- The square root of 0 is 0.
- Negative numbers do not have real square roots. Instead, their square roots are imaginary numbers.
Square roots can be represented in various forms:
- Exact form: \( \sqrt{25} = 5 \)
- Decimal form: \( \sqrt{2} \approx 1.414 \)
- Fractional form: \( \sqrt{\frac{1}{4}} = \frac{1}{2} \)
Understanding square roots is essential for solving quadratic equations, analyzing geometric properties, and performing various calculations in science and engineering. As we progress through this guide, we will explore different methods to calculate square roots, the properties of square roots, and numerous examples to deepen our understanding.
Understanding the Square Root Symbol
The square root symbol \( \sqrt{} \) is a mathematical notation used to represent the square root of a number. This symbol is also referred to as the radical sign. The number or expression inside the radical sign is called the radicand.
The general form of the square root symbol is:
\[
\sqrt{x}
\]
where \( x \) is the radicand.
Key points to understand about the square root symbol:
- The square root symbol \( \sqrt{} \) is used to denote the principal (non-negative) square root of a number. For example, \( \sqrt{25} = 5 \) because \( 5 \times 5 = 25 \).
- For any positive number \( x \), there are two square roots: \( \sqrt{x} \) (positive square root) and \( -\sqrt{x} \) (negative square root). For instance, \( \sqrt{9} = 3 \) and \( -\sqrt{9} = -3 \).
- The square root of zero is zero: \( \sqrt{0} = 0 \).
- Negative numbers do not have real square roots. Their square roots are considered imaginary numbers. For example, \( \sqrt{-4} = 2i \), where \( i \) is the imaginary unit.
Here are some examples to illustrate the use of the square root symbol:
- Exact Value: \( \sqrt{16} = 4 \) because \( 4 \times 4 = 16 \).
- Decimal Approximation: \( \sqrt{2} \approx 1.414 \), as the square root of 2 is an irrational number.
- Fraction: \( \sqrt{\frac{1}{4}} = \frac{1}{2} \) because \( \left(\frac{1}{2}\right)^2 = \frac{1}{4} \).
When dealing with square roots, it is crucial to understand the properties of the square root symbol and how it interacts with other mathematical operations:
- \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) (where \( b \neq 0 \))
- \((\sqrt{a})^2 = a\)
Understanding the square root symbol and its properties is fundamental to mastering more complex mathematical concepts and solving various types of equations. As you progress in your studies, you'll encounter the square root symbol frequently, making it a crucial part of your mathematical toolkit.
Basic Concept of Square Roots
The square root of a number is a value that, when multiplied by itself, results in the original number. Mathematically, if \( y = \sqrt{x} \), then \( y \times y = x \). Square roots are a fundamental concept in mathematics and are widely used in various applications.
Here is a step-by-step explanation of the basic concept of square roots:
- Understanding the Relationship: The square root of a number \( x \) is the number \( y \) such that \( y^2 = x \). For example, the square root of 25 is 5 because \( 5^2 = 25 \).
- Principal Square Root: The principal square root is the non-negative root of a number. It is denoted as \( \sqrt{x} \). For example, \( \sqrt{9} = 3 \), not -3.
- Positive and Negative Roots: Every positive number \( x \) has two square roots: \( \sqrt{x} \) (positive) and \( -\sqrt{x} \) (negative). For example, the square roots of 16 are 4 and -4.
- Square Root of Zero: The square root of zero is zero. Mathematically, \( \sqrt{0} = 0 \).
- Imaginary Numbers: Negative numbers do not have real square roots. Instead, their square roots are imaginary. For example, \( \sqrt{-4} = 2i \), where \( i \) is the imaginary unit, satisfying \( i^2 = -1 \).
Here are some examples to illustrate the concept of square roots:
- Example 1: \( \sqrt{36} = 6 \) because \( 6 \times 6 = 36 \).
- Example 2: \( \sqrt{49} = 7 \) because \( 7 \times 7 = 49 \).
- Example 3: \( \sqrt{0.25} = 0.5 \) because \( 0.5 \times 0.5 = 0.25 \).
- Example 4: \( \sqrt{2} \approx 1.414 \) because \( 1.414 \times 1.414 \approx 2 \). (Note: \( \sqrt{2} \) is an irrational number)
Square roots are used to solve quadratic equations, understand geometric properties, and perform various scientific and engineering calculations. Understanding the basic concept of square roots is crucial for mastering more advanced mathematical topics.
Square Root Formula
The square root formula is used to find the square root of a number. The formula is straightforward and involves the radical symbol \( \sqrt{} \). Given a number \( x \), the square root of \( x \) is denoted as \( \sqrt{x} \), which represents a value that, when multiplied by itself, equals \( x \).
The general square root formula is:
\[
\sqrt{x} = y \quad \text{where} \quad y \times y = x
\]
To understand the square root formula better, let's look at some step-by-step examples:
- Example 1: Find the square root of 64.
- Step 1: Identify the number \( x \) which is 64.
- Step 2: Apply the square root formula: \( \sqrt{64} \).
- Step 3: Find the value that, when multiplied by itself, equals 64. This value is 8 because \( 8 \times 8 = 64 \).
- Result: \( \sqrt{64} = 8 \).
- Example 2: Find the square root of 0.81.
- Step 1: Identify the number \( x \) which is 0.81.
- Step 2: Apply the square root formula: \( \sqrt{0.81} \).
- Step 3: Find the value that, when multiplied by itself, equals 0.81. This value is 0.9 because \( 0.9 \times 0.9 = 0.81 \).
- Result: \( \sqrt{0.81} = 0.9 \).
- Example 3: Find the square root of 2.
- Step 1: Identify the number \( x \) which is 2.
- Step 2: Apply the square root formula: \( \sqrt{2} \).
- Step 3: Approximate the value since 2 is not a perfect square. Using a calculator, we find \( \sqrt{2} \approx 1.414 \).
- Result: \( \sqrt{2} \approx 1.414 \).
It's important to note that the square root of negative numbers involves imaginary numbers. For example:
- The square root of -1 is represented as \( i \), where \( i \) is the imaginary unit such that \( i^2 = -1 \).
- Therefore, \( \sqrt{-4} = 2i \) because \( (2i) \times (2i) = 4i^2 = 4(-1) = -4 \).
The square root formula is fundamental in various mathematical calculations and problem-solving scenarios. Mastery of this formula allows for a deeper understanding of more advanced mathematical concepts and real-world applications.
Methods to Calculate Square Roots
There are several methods to calculate square roots, each with its own advantages and applications. Understanding these methods can help you choose the most appropriate one for different situations. Below are some of the most common methods:
- Prime Factorization Method:
This method involves breaking down a number into its prime factors and then pairing them to find the square root. Here is a step-by-step example:
- Step 1: Find the prime factors of the number. For example, for 144, the prime factors are \( 2 \times 2 \times 2 \times 2 \times 3 \times 3 \).
- Step 2: Pair the prime factors. For 144, we have pairs of \( (2 \times 2), (2 \times 2), (3 \times 3) \).
- Step 3: Take one number from each pair and multiply them together. So, \( 2 \times 2 \times 3 = 12 \).
- Result: The square root of 144 is 12.
- Long Division Method:
The long division method is a manual technique that can be used to find the square root of any number. It involves a process similar to long division. Here's how it works:
- Step 1: Group the digits of the number in pairs, starting from the decimal point. For example, 152.275 is grouped as (1)(52)(27)(5).
- Step 2: Find the largest number whose square is less than or equal to the first pair. In this case, the first pair is 1, and the largest number whose square is less than or equal to 1 is 1.
- Step 3: Subtract the square of this number from the first pair and bring down the next pair. For 152.275, we subtract 1 from 1 to get 0 and bring down 52, giving us 052.
- Step 4: Double the number found in step 2 and use it as the new divisor. Find a digit to append to the divisor and quotient such that the new number multiplied by the new digit is less than or equal to the current dividend. Continue this process until all pairs have been processed.
- Result: The square root of 152.275, calculated using this method, is approximately 12.34.
- Using a Calculator:
The simplest and most efficient way to calculate square roots is by using a calculator. Most scientific calculators have a square root function, usually represented by the symbol \( \sqrt{} \). Here's how to use it:
- Step 1: Turn on the calculator and enter the number for which you want to find the square root.
- Step 2: Press the square root button (\( \sqrt{} \)).
- Step 3: Read the result displayed on the calculator screen.
- Example: To find the square root of 225, enter 225 and press the \( \sqrt{} \) button. The display will show 15.
- Newton's Method (Newton-Raphson Method):
This iterative method is used to approximate the square root of a number. It is based on the formula:
\[
x_{n+1} = \frac{1}{2} \left( x_n + \frac{a}{x_n} \right)
\]
where \( x_n \) is the current approximation and \( a \) is the number for which we want to find the square root.- Step 1: Choose an initial approximation \( x_0 \). A good starting point is \( x_0 = \frac{a}{2} \).
- Step 2: Apply the formula iteratively to get closer approximations. For example, to find \( \sqrt{10} \):
- Initial approximation: \( x_0 = 5 \).
- First iteration: \( x_1 = \frac{1}{2} \left( 5 + \frac{10}{5} \right) = 3 \).
- Second iteration: \( x_2 = \frac{1}{2} \left( 3 + \frac{10}{3} \right) \approx 3.167 \).
- Continue iterating until the desired accuracy is achieved.
- Result: The square root of 10, approximated using Newton's method, is about 3.162.
These methods provide different approaches to finding square roots, each useful in different contexts. Mastery of these techniques can greatly enhance your problem-solving skills in mathematics.
Prime Factorization Method
The prime factorization method is a systematic way to find the square root of a number by expressing it as a product of its prime factors. This method is particularly useful for perfect squares. Here is a detailed, step-by-step guide to using the prime factorization method:
- Step 1: Prime Factorize the Number
Start by finding the prime factors of the given number. Prime factors are the prime numbers that multiply together to give the original number.
- Example: Find the prime factors of 144.
- 144 can be factorized as: \( 144 = 2 \times 2 \times 2 \times 2 \times 3 \times 3 \).
- Step 2: Pair the Prime Factors
Group the prime factors into pairs of identical factors.
- For 144: \( 144 = (2 \times 2) \times (2 \times 2) \times (3 \times 3) \).
- Step 3: Take One Factor from Each Pair
From each pair, take one factor and multiply them together. This product is the square root of the original number.
- For 144: \( \sqrt{144} = 2 \times 2 \times 3 \).
- So, \( 2 \times 2 \times 3 = 12 \).
- Step 4: Write the Final Answer
The product obtained in step 3 is the square root of the original number.
- For 144: \( \sqrt{144} = 12 \).
Let's look at another example for further clarity:
- Example: Find the square root of 324.
- Prime factorize 324: \( 324 = 2 \times 2 \times 3 \times 3 \times 3 \times 3 \).
- Group the prime factors: \( 324 = (2 \times 2) \times (3 \times 3) \times (3 \times 3) \).
- Take one factor from each pair: \( 2 \times 3 \times 3 \).
- Multiply these factors: \( 2 \times 3 \times 3 = 18 \).
- Therefore, \( \sqrt{324} = 18 \).
By following these steps, you can use the prime factorization method to efficiently calculate the square roots of perfect squares. This method is reliable and helps to understand the fundamental properties of numbers and their factors.
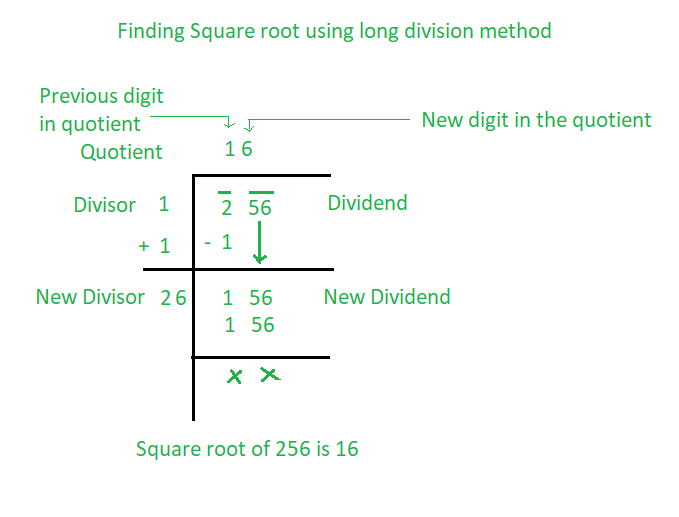
Long Division Method
The Long Division Method is a systematic approach to finding the square root of a number. This method is particularly useful for larger numbers and provides a step-by-step process to ensure accuracy. Here's how you can use the Long Division Method to calculate square roots:
- Separate the digits: Starting from the decimal point (if present), separate the digits into pairs. For whole numbers, pair the digits starting from the right. For decimal numbers, pair the digits to the right and left of the decimal point separately.
- Find the largest square: Identify the largest number whose square is less than or equal to the first pair of digits. This number is the first digit of the square root. Subtract its square from the first pair and bring down the next pair of digits.
- Double the current quotient: Double the current quotient (the part of the square root found so far) and place it as the new divisor, leaving a space for the next digit of the quotient.
- Find the next digit: Find a digit (X) such that when the new divisor (current quotient doubled with X appended) is multiplied by X, the product is less than or equal to the current dividend (the number obtained after bringing down the next pair). Append X to the quotient and the new divisor, and subtract the product from the current dividend.
- Repeat the process: Repeat steps 3 and 4 for each subsequent pair of digits. If the number is a decimal, continue the process by bringing down pairs of zeros after the decimal point until the desired precision is achieved.
Here's an example to illustrate the Long Division Method:
Example: Find the square root of 152.2756 using the Long Division Method.
- Separate into pairs: 15 22 75 60
- Find the largest square:
- 42 = 16 (too large)
- 32 = 9 (use 3)
3 is the first digit of the square root. Subtract 9 from 15, bring down 22. New number: 622.
- Double the quotient: 3 × 2 = 6. Place 6 and find X:
- Find X:
- 60X × X ≤ 622
- X = 9 (since 69 × 9 = 621, which is ≤ 622)
9 is the next digit. Quotient is now 3.9. Subtract 621 from 622, bring down 75. New number: 1750.
- Double the quotient: 39 × 2 = 78. Place 78 and find X:
- Find X:
- 780X × X ≤ 1750
- X = 2 (since 782 × 2 = 1564, which is ≤ 1750)
2 is the next digit. Quotient is now 3.92. Subtract 1564 from 1750, bring down 60. New number: 18600.
- Double the quotient: 392 × 2 = 784. Place 784 and find X:
- Find X:
- 7840X × X ≤ 18600
- X = 2 (since 7842 × 2 = 15684, which is ≤ 18600)
2 is the next digit. Quotient is now 3.922. Subtract 15684 from 18600. New number: 2916.
- Double the quotient: 3922 × 2 = 7844. Place 7844 and find X:
- Find X:
- 78440X × X ≤ 291600
- X = 3 (since 78443 × 3 = 235329, which is ≤ 291600)
3 is the next digit. Quotient is now 3.9223. Subtract 235329 from 291600. New number: 56271.
So, the square root of 152.2756 is approximately 12.345.
Using a Calculator to Find Square Roots
Finding the square root of a number using a calculator is a straightforward process. Most scientific and even basic calculators have a square root function. Follow these steps to find the square root of a number:
- Turn on your calculator.
- Enter the number for which you want to find the square root.
- Press the square root button (√ or √). This button is usually located above one of the numerical keys, often the 2 or 3 key. On scientific calculators, you may need to press the 'Shift' or '2nd' button before pressing the square root button.
- Read the result displayed on the calculator screen. This is the square root of the number you entered.
Here is an example:
- Example 1: Finding the square root of 16.
- Enter 16.
- Press the square root button (√).
- The display will show 4, since √16 = 4.
For calculators that do not have a square root button, you can use the exponentiation feature if available. Follow these steps:
- Turn on your calculator.
- Enter the number for which you want to find the square root.
- Press the exponentiation button (^ or xy).
- Enter 0.5 (since the square root of a number is the same as raising that number to the power of 0.5).
- Press the equals button (=) or execute the calculation.
- Read the result displayed on the calculator screen. This is the square root of the number you entered.
Here is another example using exponentiation:
- Example 2: Finding the square root of 25.
- Enter 25.
- Press the exponentiation button (^).
- Enter 0.5.
- Press the equals button (=).
- The display will show 5, since 250.5 = 5.
Using these methods, you can quickly and accurately find the square root of any number using a calculator.

Examples of Square Root Calculations
Understanding how to calculate square roots is essential for solving various mathematical problems. Below are some detailed examples illustrating different methods for finding square roots.
Example 1: Square Root of a Perfect Square
The simplest case is finding the square root of a perfect square. For instance, the square root of 16.
- This is because \(4 \times 4 = 16\).
Example 2: Square Root of a Non-Perfect Square
Finding the square root of a non-perfect square, like 20, can be more challenging. This example uses approximation.
- Using a calculator or long division method, we find that the square root of 20 is approximately 4.472.
Example 3: Prime Factorization Method
To find the square root of 1764 using the prime factorization method:
- Factorize 1764 into its prime factors:
- Group the prime factors into pairs:
- Take one number from each pair and multiply them:
Thus, the square root of 1764 is 42.
Example 4: Using a Calculator
Calculators are a quick way to find square roots. For example, to find the square root of 50:
- Enter 50 into the calculator.
- Press the square root (√) button.
- The display shows approximately 7.071.
Thus, .
Example 5: Long Division Method
The long division method is useful for finding square roots of large numbers, such as 2025:
- Pair the digits from right to left: 20 | 25.
- Find the largest number whose square is less than or equal to 20: \(4^2 = 16\).
- Subtract and bring down the next pair: \(20 - 16 = 4\), bring down 25 to get 425.
- Double the quotient and find a digit to form the new divisor: 40_. The digit 5 works because \(405 \times 5 = 2025\).
- The square root of 2025 is thus 45.
Conclusion
These examples illustrate different methods to calculate square roots, highlighting their applicability in various contexts, from perfect squares to more complex numbers. Practicing these methods can help deepen your understanding and proficiency in solving square root problems.
Simple Square Root Examples
The square root of a number is a value that, when multiplied by itself, gives the original number. Let's explore some simple square root examples using basic numbers and perfect squares.
- Example 1: Square Root of 4
\(\sqrt{4} = 2\)
Explanation: 2 multiplied by 2 equals 4. Therefore, the square root of 4 is 2.
- Example 2: Square Root of 9
\(\sqrt{9} = 3\)
Explanation: 3 multiplied by 3 equals 9. Hence, the square root of 9 is 3.
- Example 3: Square Root of 16
\(\sqrt{16} = 4\)
Explanation: 4 multiplied by 4 equals 16. Therefore, the square root of 16 is 4.
- Example 4: Square Root of 25
\(\sqrt{25} = 5\)
Explanation: 5 multiplied by 5 equals 25. Hence, the square root of 25 is 5.
- Example 5: Square Root of 36
\(\sqrt{36} = 6\)
Explanation: 6 multiplied by 6 equals 36. Therefore, the square root of 36 is 6.
These examples illustrate the basic concept of finding the square root of perfect squares. Understanding these simple cases helps build a foundation for tackling more complex square root problems.
Complex Square Root Examples
In this section, we will explore more complex square root examples, involving larger numbers and those that are not perfect squares. Understanding these examples will help in grasping the application of square root formulas in various contexts.
Example 1: Square Root of a Non-Perfect Square
Let's find the square root of 50 using the prime factorization method:
- Prime factorize 50: \(50 = 2 \times 5 \times 5\)
- Group the prime factors into pairs: \((5 \times 5) \times 2\)
- Extract the square root of the perfect square: \(5\)
- Combine the results: \( \sqrt{50} = 5\sqrt{2} \)
Therefore, the square root of 50 is \( 5\sqrt{2} \).
Example 2: Using the Long Division Method
Let's find the square root of 12345 using the long division method:
- Pair the digits of 12345 from right to left: \(12 | 34 | 5\)
- Find the largest number whose square is less than or equal to 12: \(3^2 = 9\)
- Subtract and bring down the next pair: \(12 - 9 = 3\), new number is \(345\)
- Double the divisor (3): \(3 \times 2 = 6\)
- Find the digit \(d\) such that \(60d \times d \leq 345\). Here, \(60 \times 5 = 300\).
- Subtract and repeat: \(345 - 300 = 45\), bring down next digit (0 if none left), making \(4500\).
- Continue the process until desired precision.
This method gives a detailed step-by-step approximation of the square root.
Example 3: Complex Number Square Root
For complex numbers, finding square roots involves imaginary units. Let's find the square root of \(-25\):
- Recognize that \( \sqrt{-25} = \sqrt{25} \times \sqrt{-1} \)
- Calculate the square root of 25: \(5\)
- Square root of \(-1\) is \(i\) (the imaginary unit)
- Combine the results: \( \sqrt{-25} = 5i \)
Thus, the square root of \(-25\) is \(5i\).
Example 4: Solving a Quadratic Equation Using Square Roots
Solve \(x^2 - 16 = 0\) using square roots:
- Rewrite the equation: \(x^2 = 16\)
- Take the square root of both sides: \(x = \pm \sqrt{16}\)
- Calculate the square roots: \(x = \pm 4\)
The solutions to the equation are \(x = 4\) and \(x = -4\).
These examples illustrate various techniques for finding square roots, including dealing with non-perfect squares, using the long division method, handling complex numbers, and solving quadratic equations.
Square Roots of Perfect Squares
A perfect square is a number that can be expressed as the product of an integer with itself. Finding the square root of a perfect square is straightforward because it results in an integer.
Here are some common perfect squares and their square roots:
- \(\sqrt{1} = 1\)
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
- \(\sqrt{16} = 4\)
- \(\sqrt{25} = 5\)
- \(\sqrt{36} = 6\)
- \(\sqrt{49} = 7\)
- \(\sqrt{64} = 8\)
- \(\sqrt{81} = 9\)
- \(\sqrt{100} = 10\)
Let's take a step-by-step approach to find the square root of a perfect square using two methods:
Prime Factorization Method
To find the square root using the prime factorization method, follow these steps:
- Factorize the number into its prime factors.
- Group the prime factors into pairs of equal factors.
- Take one factor from each pair and multiply them together to get the square root.
Example:
Find the square root of 144.
- Prime factorization: \(144 = 2 \times 2 \times 2 \times 2 \times 3 \times 3\)
- Group into pairs: \((2 \times 2) \times (2 \times 2) \times (3 \times 3)\)
- Take one from each pair: \(2 \times 2 \times 3 = 12\)
- So, \(\sqrt{144} = 12\)
Long Division Method
To find the square root using the long division method, follow these steps:
- Place a bar over every pair of digits of the number starting from the right.
- Find the largest number whose square is less than or equal to the first group (starting from the left). This number is the divisor and the quotient.
- Subtract the product of the divisor and quotient from the first group and bring down the next group of digits to the right.
- Double the quotient and write it as the new divisor with a blank space next to it.
- Find the largest digit to fill the blank space so that the new divisor times this digit is less than or equal to the current number. This digit is added to the quotient.
- Repeat steps 3-5 until all groups have been brought down.
Example:
Find the square root of 529.
- Place bars: \( \overline{5} \overline{29} \)
- The largest number whose square is ≤ 5 is 2 (\(2^2 = 4\)). Subtract \(4\) from \(5\), get \(1\). Bring down \(29\) to make \(129\).
- Double the quotient (2), making 4. Find the largest digit (3) to complete \(43 \times 3 = 129\).
- The quotient is 23, so \(\sqrt{529} = 23\).
Understanding these methods can help in finding the square roots of perfect squares efficiently.

Square Roots of Non-Perfect Squares
Finding the square roots of non-perfect squares can be challenging because they do not result in whole numbers. Here, we will explore various methods to find the approximate values of these square roots.
Using the Long Division Method
The long division method provides a systematic way to find the square roots of non-perfect squares to a desired number of decimal places.
Start by grouping the digits of the number in pairs, starting from the decimal point. For example, to find the square root of 50, write it as 50.00 and group as (50)(00).
Find the largest number whose square is less than or equal to the first group. For 50, the largest square is 72 = 49. Write 7 as the first digit of the square root.
Subtract the square from the first group and bring down the next group. Here, 50 - 49 = 1, and bring down 00 to make 100.
Double the number found in step 2 (7 becomes 14) and find a digit (x) such that 14x * x is less than or equal to 100. The digit is 0 (since 140*0 = 0).
Repeat the process with the remainder. Continue bringing down pairs of zeros, doubling the current root, and finding the next digit.
Example: Finding √50 using Long Division
50.00 → (50)(00)
72 = 49, 50 - 49 = 1, bring down 00 → 100
Double 7: 14, find x: 140x ≤ 100 → x = 0
Continue with next pairs of zeros...
Following this method, you can approximate √50 ≈ 7.071.
Using Estimation Method
Estimation is a quicker but less precise method compared to long division. Here are the steps:
Identify the two perfect squares between which the number lies. For 50, it lies between 49 (72) and 64 (82).
Estimate the square root by averaging the two boundary values. For 50, we start with an average of 7 and 8, giving us 7.5.
Refine the estimate by using the formula: (Lower Bound + Upper Bound) / 2 and checking the result.
Example: Finding √50 by Estimation
50 is between 49 (72) and 64 (82).
Average: (7 + 8) / 2 = 7.5
Refine: 7.071 ≈ √50 (using iterative averaging)
Using a Calculator
The simplest method for finding the square root of a non-perfect square is to use a calculator:
Enter the number (e.g., 50) into the calculator.
Press the square root (√) button to get the result.
The display will show the square root of the number. For 50, it will show approximately 7.071.
These methods help to find the square roots of non-perfect squares accurately. Understanding and practicing these methods will improve your ability to handle square roots in various mathematical problems.
Applications of Square Roots
Square roots have numerous applications in various fields, including mathematics, science, engineering, and everyday life. Here are some common applications:
- Mathematics:
- Solving Quadratic Equations: Square roots are used to find the solutions of quadratic equations of the form \(ax^2 + bx + c = 0\) using the quadratic formula: \[ x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{2a} \]
- Geometry: Square roots help in calculating the lengths of sides in right-angled triangles using the Pythagorean theorem: \[ c = \sqrt{a^2 + b^2} \] where \(c\) is the hypotenuse and \(a\) and \(b\) are the other two sides.
- Science:
- Physics: Square roots are used in formulas such as calculating the root mean square velocity of gas molecules: \[ v_{\text{rms}} = \sqrt{\frac{3kT}{m}} \] where \(k\) is the Boltzmann constant, \(T\) is the temperature, and \(m\) is the mass of a molecule.
- Acoustics: In acoustics, the intensity of sound is often calculated using square roots to determine sound pressure levels.
- Engineering:
- Structural Engineering: Square roots are used to calculate the natural frequency of structures and mechanical systems, which is crucial for ensuring stability and safety.
- Electrical Engineering: In electrical engineering, square roots are used to calculate the root mean square (RMS) values of alternating currents and voltages: \[ V_{\text{RMS}} = \frac{V_{\text{peak}}}{\sqrt{2}} \]
- Everyday Life:
- Cooking and Baking: When scaling recipes, square roots can be used to adjust ingredient quantities proportionally.
- Financial Calculations: Square roots are used in finance to calculate compound interest and to understand the standard deviation of investment returns, which helps in assessing risk.
Understanding the applications of square roots is essential for solving practical problems in various disciplines and improving problem-solving skills.
Square Roots in Geometry
The concept of square roots is deeply embedded in geometry, particularly in the study of right-angled triangles, areas, and distances. Here are some fundamental applications and examples:
1. The Pythagorean Theorem
One of the most well-known applications of square roots in geometry is the Pythagorean Theorem. This theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
The formula is given by:
\[ c^2 = a^2 + b^2 \]
Where \( c \) is the length of the hypotenuse, and \( a \) and \( b \) are the lengths of the other two sides. To find the length of the hypotenuse, we take the square root of the sum of the squares of the other two sides:
\[ c = \sqrt{a^2 + b^2} \]
Example:
Given a right-angled triangle where \( a = 3 \) units and \( b = 4 \) units, find the length of the hypotenuse \( c \).
Solution:
\[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{ units} \]
2. Distance Formula
The distance formula is used to determine the distance between two points in a plane. If we have two points \((x_1, y_1)\) and \((x_2, y_2)\), the distance \(d\) between these points is given by:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Example:
Find the distance between the points \((1, 2)\) and \((4, 6)\).
Solution:
\[ d = \sqrt{(4 - 1)^2 + (6 - 2)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{ units} \]
3. Area of a Square
The area \(A\) of a square can be found if we know the length of one of its sides \(s\). The formula is:
\[ A = s^2 \]
Conversely, if we know the area of the square, we can find the side length by taking the square root of the area:
\[ s = \sqrt{A} \]
Example:
If the area of a square is 49 square units, find the length of its side.
Solution:
\[ s = \sqrt{49} = 7 \text{ units} \]
4. Diagonal of a Square
The diagonal of a square can be found using the relationship between the side length and the diagonal. If \( s \) is the side length of the square, the diagonal \(d\) is given by:
\[ d = s\sqrt{2} \]
Example:
If the side length of a square is 5 units, find the length of the diagonal.
Solution:
\[ d = 5\sqrt{2} \approx 5 \times 1.414 = 7.07 \text{ units} \]
5. Applications in Circles
Square roots also appear in circle geometry. For instance, if we know the area \(A\) of a circle, we can find the radius \(r\) using the formula:
\[ A = \pi r^2 \rightarrow r = \sqrt{\frac{A}{\pi}} \]
Example:
If the area of a circle is 50.24 square units, find the radius. (Use \(\pi \approx 3.14\))
Solution:
\[ r = \sqrt{\frac{50.24}{3.14}} \approx \sqrt{16} = 4 \text{ units} \]
Conclusion
Understanding square roots is essential for solving many geometric problems, from basic calculations involving triangles and squares to more complex applications in various shapes and distances.
Square Roots in Algebra
Square roots play a significant role in algebra, especially when solving equations and understanding functions. Here, we will explore various aspects of square roots in algebra, including solving equations, properties, and practical examples.
Solving Equations Involving Square Roots
To solve equations that involve square roots, you typically need to isolate the square root term and then square both sides of the equation to eliminate the square root. Here are the steps:
- Isolate the square root term on one side of the equation.
- Square both sides of the equation to eliminate the square root.
- Solve the resulting equation.
- Check your solutions to ensure they do not produce extraneous results.
For example, consider the equation:
\[\sqrt{x + 3} = 5\]
Step 1: Isolate the square root term (already isolated).
Step 2: Square both sides:
\[(\sqrt{x + 3})^2 = 5^2\]
This simplifies to:
\[x + 3 = 25\]
Step 3: Solve for \(x\):
\[x = 25 - 3\]
\[x = 22\]
Step 4: Check the solution by substituting back into the original equation:
\[\sqrt{22 + 3} = 5\]
\[\sqrt{25} = 5\]
Since this is true, \(x = 22\) is a valid solution.
Properties of Square Roots in Algebra
Square roots have several important properties that are frequently used in algebraic manipulations:
- \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) (for \(b \neq 0\))
- \((\sqrt{a})^2 = a\)
- \(\sqrt{a^2} = |a|\)
Examples of Square Roots in Algebraic Expressions
Let's look at how square roots can be incorporated into various algebraic expressions and their simplifications.
Example 1: Simplify the expression:
\(\sqrt{50} + \sqrt{8}\)
First, factor each radicand to identify perfect squares:
\(\sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}\)
\(\sqrt{8} = \sqrt{4 \cdot 2} = \sqrt{4} \cdot \sqrt{2} = 2\sqrt{2}\)
Combine like terms:
\(5\sqrt{2} + 2\sqrt{2} = 7\sqrt{2}\)
Example 2: Solve for \(x\) in the equation:
\[x^2 - 4x + 4 = 16\]
Step 1: Simplify the equation by moving all terms to one side:
\[x^2 - 4x + 4 - 16 = 0\]
\[x^2 - 4x - 12 = 0\]
Step 2: Factor the quadratic equation:
\[(x - 6)(x + 2) = 0\]
Step 3: Solve for \(x\):
\[x - 6 = 0 \quad \text{or} \quad x + 2 = 0\]
\[x = 6 \quad \text{or} \quad x = -2\]
Conclusion
Understanding and applying square roots in algebra is essential for solving equations and simplifying expressions. By following the steps and properties outlined, you can effectively manage square root terms in various algebraic contexts.

Real-Life Applications of Square Roots
The concept of square roots is not just limited to theoretical mathematics but has a wide range of real-life applications. Here are some practical uses of square roots:
-
Architecture and Construction:
In architecture, square roots are used to calculate the dimensions of various elements in a structure. For example, when determining the diagonal length of a square or rectangular plot of land, architects use the Pythagorean theorem, which involves square roots. If you have a square with sides of length \(a\), the diagonal \(d\) is calculated using \(d = \sqrt{2} \times a\).
-
Physics:
In physics, square roots appear in formulas dealing with wave motion, quantum mechanics, and relativity. For instance, the de Broglie wavelength of a particle is inversely proportional to the square root of its kinetic energy.
-
Engineering:
Engineers frequently use square roots when dealing with forces and stresses. For example, in calculating the load that a beam can support, engineers use formulas that include square roots to determine the beam’s deflection and bending stress.
-
Astronomy:
Astronomers use square roots in calculating gravitational forces and orbital speeds. For instance, the escape velocity \(v_e\) from a planet is given by \(v_e = \sqrt{2 \cdot G \cdot M / r}\), where \(G\) is the gravitational constant, \(M\) is the mass of the planet, and \(r\) is the radius from the center of the planet to the point of escape.
-
Finance:
In finance, the square root is used in various risk assessment and statistical formulas. For instance, the standard deviation, a measure of market volatility, involves the square root of the variance.
-
Medical Imaging:
Square roots are used in medical imaging techniques like MRI and CT scans to process the data and create clear images of the internal structures of the body.
-
Computer Graphics:
In computer graphics, square roots are used in algorithms for rendering, collision detection, and distance calculations between points in 3D space. For example, the Euclidean distance between two points \((x_1, y_1, z_1)\) and \((x_2, y_2, z_2)\) is calculated using the formula \(\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}\).
Overall, the square root is a fundamental mathematical operation that is vital in various fields, enabling accurate calculations and contributing to advancements in technology, science, and engineering.
Common Mistakes and Misconceptions
Understanding square roots can be challenging, and there are several common mistakes and misconceptions that students often encounter. Here, we will discuss some of these issues and provide tips on how to avoid them.
-
Misinterpreting the Square Root Symbol:
The square root symbol (√) represents the principal (positive) square root. A common mistake is assuming that √x can be negative. For example, √9 is 3, not -3. However, the equation x² = 9 has two solutions, 3 and -3, but √9 specifically refers to the positive root.
-
Forgetting the Plus-Minus Sign:
When solving equations involving square roots, it is important to remember that taking the square root of both sides of an equation involves both the positive and negative roots. For instance, if x² = 25, then x = ±5. Neglecting the negative root can lead to incomplete solutions.
-
Confusing Square and Square Root Operations:
Squaring a number and taking the square root are inverse operations, but they are not the same. For example, (√4)² = 4, but √(4²) = 4. It is crucial to understand when to apply each operation correctly.
-
Incorrectly Simplifying Square Roots:
Simplifying square roots requires understanding how to break down the radicand (the number inside the square root). For example, √18 can be simplified to 3√2 because 18 = 9 × 2 and √9 = 3. Failing to simplify square roots properly can lead to errors in calculations.
-
Misapplying the Product and Quotient Rules:
The product rule states that √(a × b) = √a × √b, and the quotient rule states that √(a/b) = √a / √b. Misapplying these rules can result in incorrect answers. For instance, √(4 × 9) = √36 = 6, but if misapplied as √4 × √9, it still results in 6, but the process must be understood correctly to avoid mistakes in more complex problems.
-
Assuming All Square Roots Are Rational:
Not all square roots are rational numbers. For example, √2 is an irrational number and cannot be expressed as a simple fraction. Recognizing when a square root is irrational is important for accurate mathematical reasoning.
By being aware of these common mistakes and misconceptions, students can improve their understanding and accuracy when working with square roots.
Xem video để học cách tính căn bậc hai - một trong những con số đã thay đổi toán học mãi mãi.
Cách tính căn bậc hai - Các con số đã thay đổi toán học mãi mãi
READ MORE:
Khám phá phương pháp Newton để tính căn bậc hai nhanh nhất. Video này giải thích cách áp dụng phương pháp này một cách đơn giản và hiệu quả.
Phương Pháp Nhanh Nhất Để Tính Căn Bậc Hai: Phương Pháp Newton