Topic square root with variables calculator: Discover the power of a Square Root with Variables Calculator in simplifying complex algebraic expressions. This tool effortlessly handles polynomials and equations involving variables, providing accurate results in seconds. Perfect for students, educators, and anyone looking to enhance their mathematical skills. Start mastering algebra today with our comprehensive guide and user-friendly calculator.
Table of Content
- Square Root with Variables Calculator
- Introduction
- What is a Square Root with Variables?
- How to Calculate Square Roots with Variables
- Step-by-Step Guide
- Examples of Square Root with Variables
- Using a Square Root with Variables Calculator
- Benefits of Using a Calculator
- Common Mistakes to Avoid
- Advanced Techniques
- Applications in Real Life
- FAQs
- Conclusion
- YOUTUBE: Video hướng dẫn cách đơn giản hóa căn bậc hai với biến số. Thích hợp cho học sinh và giáo viên muốn nâng cao kỹ năng toán học.
Square Root with Variables Calculator
This calculator helps to find the square root of expressions involving variables. Simply input the expression, and the calculator will compute the square root.
How to Use the Calculator
- Enter the mathematical expression involving variables.
- Ensure the expression is in a form where taking the square root is feasible (e.g., a perfect square).
- Click on the "Calculate" button to get the result.
Examples
-
Expression: \( x^2 + 4x + 4 \)
Square Root: \( \sqrt{x^2 + 4x + 4} = |x + 2| \)
-
Expression: \( 9y^2 - 24y + 16 \)
Square Root: \( \sqrt{9y^2 - 24y + 16} = |3y - 4| \)
Calculator
Features
- Handles polynomials and other algebraic expressions.
- Supports multiple variables.
- Instant calculation with real-time results.
Advantages
- Simplifies complex expressions.
- Helps in solving algebraic equations.
- Facilitates learning and understanding of algebra.

READ MORE:
Introduction
A Square Root with Variables Calculator is an essential tool for simplifying and solving algebraic expressions that involve variables. This tool can break down complex equations into more manageable forms, making it easier to understand and solve them. Whether you are a student, teacher, or math enthusiast, understanding how to work with square roots and variables is crucial in various mathematical contexts.
Here's a step-by-step guide to help you get started:
- Enter the algebraic expression into the calculator. Ensure the expression is correctly formatted, including any variables and constants.
- Verify that the expression under the square root is a perfect square. If not, the calculator may provide a simplified form or an approximation.
- Click the "Calculate" button to process the expression. The calculator will display the square root of the given algebraic expression.
For example, given the expression \( x^2 + 6x + 9 \), the calculator will find:
\[ \sqrt{x^2 + 6x + 9} = \sqrt{(x + 3)^2} = |x + 3| \]
This capability is invaluable for simplifying equations and solving for variables in both basic and advanced mathematics. Utilizing a Square Root with Variables Calculator can save time and reduce errors, making it an indispensable tool for anyone working with algebraic expressions.
What is a Square Root with Variables?
The concept of a square root with variables involves finding the root of an expression that contains both numbers and variables. In mathematical terms, the square root of a number x is a value that, when multiplied by itself, gives x. When variables are introduced, the process involves similar principles but requires additional steps to handle the variables.
Consider the general form of a square root with variables:
\[\sqrt{a \cdot x^n}\]
Here, \(a\) is a coefficient, \(x\) is the variable, and \(n\) is the exponent of the variable. The goal is to simplify the expression under the square root.
Steps to Simplify Square Roots with Variables
- Identify and separate the coefficients and the variable parts of the expression.
- Factor the expression to identify perfect squares.
- Apply the square root to each part separately.
For example, let's simplify the square root of \( 9x^6 \):
- Factor inside the radical: \(\sqrt{9 \cdot x^6}\)
- Recognize the perfect squares: \(\sqrt{(3^2) \cdot (x^3)^2}\)
- Take the square root of each part: \(3 \cdot |x^3|\)
Thus, \(\sqrt{9x^6} = 3|x^3|\).
Properties of Square Roots
- Multiplicative Property: \(\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}\)
- Quotient Property: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- Equality Property: If \(x^2 = a\), then \(x = \pm\sqrt{a}\)
Examples
Consider the following examples to illustrate the process:
Example 1: Simplify \(\sqrt{100x^2y^4}\)
- Factor: \(\sqrt{(10^2) \cdot (x^2) \cdot (y^2)^2}\)
- Apply the square root: \(10 \cdot |x| \cdot y^2\)
- Result: \(10|x|y^2\)
Example 2: Solve \(\sqrt{(x - 2)} = 5\)
- Square both sides: \(x - 2 = 25\)
- Solve for \(x\): \(x = 27\)
Understanding and simplifying square roots with variables is essential in algebra, allowing for the solving of more complex equations and the simplification of expressions in various fields of mathematics.
How to Calculate Square Roots with Variables
Calculating square roots with variables involves understanding basic algebraic principles and applying square root properties. Here’s a step-by-step guide to help you through the process:
-
Identify the Expression: Determine the variable expression under the square root. For example, consider the expression \(\sqrt{a^2}\).
-
Factorize the Expression: Break down the variable and its coefficient into prime factors. For instance, for \(\sqrt{64x^8}\), factorize \(64\) and \(x^8\).
\(\begin{align}
\sqrt{64x^8} &= \sqrt{(2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2) \cdot (x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x)} \\
&= 2^3 \cdot x^4 \\
&= 8x^4
\end{align}\) -
Simplify the Square Root: Apply the property \(\sqrt{a^2} = a\). Use this to simplify each term inside the square root.
For example, simplify \(\sqrt{225x^4}\):
\(\begin{align}
\sqrt{225x^4} &= \sqrt{(15 \cdot 15) \cdot (x^2 \cdot x^2)} \\
&= 15x^2
\end{align}\) -
Handle Complex Expressions: For more complex expressions, break them down step by step.
Example: \(\sqrt{784x^2}\)
\(\begin{align}
\sqrt{784x^2} &= \sqrt{(28 \cdot 28) \cdot (x \cdot x)} \\
&= 28x
\end{align}\) -
Use an Online Calculator: For complicated expressions, consider using an online square root calculator which can simplify expressions involving variables.
By following these steps, you can simplify and calculate the square roots of variable expressions effectively. Regular practice and familiarity with algebraic properties will make the process more intuitive over time.
Step-by-Step Guide
Calculating the square roots with variables involves a series of steps that simplify the process. Here is a detailed step-by-step guide:
-
Identify the Expression: Start by identifying the expression under the square root. For example, let's consider the expression \(\sqrt{64x^8}\).
-
Factorize the Expression: Factorize the numerical and variable parts separately.
- For the numerical part, 64 can be factored as \(64 = 2^6\).
- For the variable part, \(x^8\) can be written as \(x \times x \times x \times x \times x \times x \times x \times x\) or \((x^4)^2\).
-
Apply Square Root Properties: Use the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) to separate the square root.
- \(\sqrt{64x^8} = \sqrt{64} \times \sqrt{x^8}\)
-
Calculate the Square Roots: Calculate the square roots of the factored parts.
- \(\sqrt{64} = 8\)
- \(\sqrt{x^8} = (x^4)\), because the square root of \(x^8\) is \(x^4\).
-
Combine the Results: Combine the square roots of the numerical and variable parts.
- \(\sqrt{64x^8} = 8x^4\)
Let’s consider another example, \(\sqrt{225x^4}\):
- Factorize: \(225 = 15^2\) and \(x^4 = (x^2)^2\).
- Apply the square root property: \(\sqrt{225x^4} = \sqrt{225} \times \sqrt{x^4}\).
- Calculate the square roots: \(\sqrt{225} = 15\) and \(\sqrt{x^4} = x^2\).
- Combine the results: \(\sqrt{225x^4} = 15x^2\).
This method can be applied to any variable expression under a square root, ensuring a clear and systematic approach to simplification.

Examples of Square Root with Variables
Understanding how to calculate square roots with variables can be made clearer through examples. Let's look at a few illustrative cases:
-
Example 1: Square root of \(64x^8\)
First, factor the expression:
\(\sqrt{64x^8} = \sqrt{(8x^4)^2}\)
Since the square root of a square is the base itself, we get:
\(\sqrt{64x^8} = 8x^4\)
-
Example 2: Square root of \(225x^4\)
Factor the expression:
\(\sqrt{225x^4} = \sqrt{(15x^2)^2}\)
Thus, the solution is:
\(\sqrt{225x^4} = 15x^2\)
-
Example 3: Square root of \(784x^2\)
Factor the expression:
\(\sqrt{784x^2} = \sqrt{(28x)^2}\)
So, the square root is:
\(\sqrt{784x^2} = 28x\)
-
Example 4: Square root of \(32x^4y^{10}z\)
First, factorize each component:
\(\sqrt{32x^4y^{10}z} = \sqrt{(16x^4y^{10})(2z)}\)
We simplify as follows:
\(\sqrt{16x^4y^{10}} \times \sqrt{2z} = 4x^2y^5 \times \sqrt{2z}\)
Thus, the result is:
\(4x^2y^5\sqrt{2z}\)
Using a Square Root with Variables Calculator
A square root with variables calculator is a useful tool for simplifying expressions involving the square roots of variables. These calculators can handle complex expressions and provide accurate results quickly. Here’s how to use one effectively:
-
Access the Calculator:
Find a reliable online square root with variables calculator by searching for terms like "square root with variables calculator" on your preferred search engine.
-
Input the Expression:
Enter the mathematical expression that includes the square root and variable(s) into the calculator’s input field. For example, if you have √(x^2 + 4x + 4), type it exactly as it appears.
-
Use Proper Syntax:
Ensure that you use the correct syntax for the square root and variables. Most calculators require you to use symbols like √ for square roots and letters for variables. Some calculators might use sqrt() instead of the √ symbol.
-
Submit the Expression:
Click the calculate or equivalent button to process the expression. The calculator will then compute the square root of the variable expression and display the result.
-
Review the Result:
Check the output to ensure it matches your expectations. The result should show the simplified form of the square root expression involving the variable.
For a better understanding, let's look at a specific example:
Example:
Suppose you want to simplify the expression √(x^2 + 6x + 9). Here’s how you would do it using the calculator:
- Input the expression: √(x^2 + 6x + 9)
- Submit the expression.
- Review the output: The calculator simplifies this to |x + 3|, which is the absolute value of (x + 3).
By following these steps, you can easily use a square root with variables calculator to simplify and solve expressions involving square roots and variables. These calculators are especially helpful for verifying your work and saving time on complex problems.
Benefits of Using a Calculator
Using a square root calculator with variables offers numerous advantages for both students and professionals. Here are some key benefits:
- Accuracy: Calculators ensure precise calculations, minimizing the risk of human error. This is particularly important in complex mathematical problems involving variables.
- Speed: Calculators provide instant results, saving time compared to manual calculations. This is especially useful in time-sensitive situations such as exams or work deadlines.
- Convenience: Online calculators are easily accessible from any device with an internet connection. This allows for quick and easy computations without the need for physical calculators or reference materials.
- Step-by-Step Solutions: Many calculators, such as those provided by Symbolab and Mathway, offer step-by-step solutions. This helps users understand the process and learn how to solve similar problems independently.
- Versatility: Square root calculators can handle a wide range of expressions, including those with complex variables. This makes them versatile tools for various mathematical disciplines.
- Educational Value: By using calculators, students can focus on learning concepts rather than getting bogged down by arithmetic. This enhances their overall understanding and retention of mathematical principles.
- Advanced Functions: Modern calculators come with advanced features that allow for the manipulation of variables, providing solutions in both exact and decimal forms.
In summary, a square root calculator with variables is an invaluable tool for anyone dealing with mathematical problems. It enhances accuracy, saves time, and provides educational benefits that aid in the comprehension of complex concepts.
Common Mistakes to Avoid
When using a square root with variables calculator, it's essential to be aware of common mistakes that can lead to incorrect results. Here are some frequent errors and how to avoid them:
-
Ignoring the Absolute Value:
When simplifying square roots involving variables, don't forget to include absolute value signs when necessary. For example, \(\sqrt{x^2} = |x|\). This accounts for both positive and negative values of the variable.
-
Incorrect Factorization:
Ensure you correctly factorize the expression inside the square root. Misidentifying factors can lead to incorrect simplification. For instance, \(\sqrt{9x^6}\) should be simplified as \(\sqrt{(3^2)(x^3)^2} = 3|x^3|\), not \(\sqrt{9}\sqrt{x^6} = 3x^3\).
-
Combining Non-Like Terms:
Avoid combining square roots of different terms incorrectly. For example, \(\sqrt{a} + \sqrt{b} \neq \sqrt{a + b}\). Only like terms under the square root can be combined or simplified together.
-
Forgetting to Simplify Completely:
Always simplify the expression inside the square root as much as possible before calculating. For example, simplify \(\sqrt{50x^4}\) to \(\sqrt{25 \cdot 2 \cdot x^4}\) which further reduces to \(5x^2\sqrt{2}\).
-
Incorrect Use of Square Root Properties:
Apply the properties of square roots correctly. For instance, \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\) and \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\), not \(\sqrt{a + b}\) or \(\sqrt{a - b}\).
By being mindful of these common mistakes, you can ensure more accurate results when using a square root with variables calculator.

Advanced Techniques
Using a square root with variables calculator can be enhanced by employing various advanced techniques to solve complex expressions. These techniques help simplify and solve equations more efficiently.
1. Rationalizing the Denominator
Rationalizing the denominator involves eliminating radicals from the denominator of a fraction. This can be done by multiplying both the numerator and the denominator by a suitable radical.
- Identify the radical in the denominator.
- Multiply both the numerator and the denominator by the conjugate of the denominator if it involves a binomial, or by the same radical if it is a single term.
- Simplify the resulting expression.
Example:
\(\frac{5}{\sqrt{3}}\) can be rationalized as follows:
2. Simplifying Nested Radicals
Nesting radicals can make expressions complex. Simplifying nested radicals involves breaking them down step-by-step:
- Look for patterns or perfect squares/cubes within the radicals.
- Use properties of exponents and radicals to simplify.
- Combine like terms where possible.
Example:
Simplify \(\sqrt{50 + \sqrt{24}}\):
3. Using Product and Quotient Rules
Applying the product and quotient rules for radicals can help in breaking down complex expressions:
- Product Rule: \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- Quotient Rule: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
Example:
Simplify \(\sqrt{\frac{9x^6}{y^3z^9}}\):
4. Handling Higher-Order Roots
When dealing with higher-order roots, it's essential to factor expressions appropriately:
- Express variables and constants as powers.
- Apply the \(n\)th root rule: \(\sqrt[n]{a^m} = a^{m/n}\).
- Simplify using exponent rules.
Example:
Simplify \(\sqrt[4]{81a^4b^5}\):
5. Solving Radical Equations
To solve equations involving radicals:
- Isolate the radical expression on one side of the equation.
- Square both sides of the equation to eliminate the radical.
- Solve the resulting polynomial equation.
- Check all solutions in the original equation to discard extraneous solutions.
Example:
Solve \(\sqrt{x+3} = x - 1\):
Thus, \(x = 1\) or \(x = 2\). Verify both solutions in the original equation.
Applications in Real Life
Square roots involving variables have numerous real-life applications across various fields. Below are some detailed examples:
- Geometry and Construction: Square roots are essential in calculating distances and measurements. For example, to find the diagonal length of a rectangular space, such as a room or a construction site, you can use the Pythagorean theorem, which involves square roots. This is crucial in ensuring structures are built accurately.
- Physics: In physics, square roots are used to determine quantities such as the velocity of an object in motion or the intensity of sound waves. For instance, the formula for the speed of an object falling under gravity involves the square root of the height from which it falls.
- Statistics: Square roots are used to calculate standard deviation, a measure of the dispersion of a set of data points. This is important for data analysis, helping statisticians understand the variability within data sets.
- Finance: In finance, square roots are used in the calculation of stock volatility. The standard deviation of stock returns, which helps in assessing the risk associated with an investment, involves taking the square root of the variance.
- Computer Graphics: Square roots are frequently used in computer graphics to calculate distances between points in 2D and 3D space. This is crucial for rendering images and animations accurately.
- Engineering: Engineers use square roots to determine the natural frequency of structures like bridges and buildings. This helps predict how these structures will respond to various forces, such as wind or traffic loads.
- Navigation: In navigation, square roots are used to compute the distance between two points on a map. This is critical for plotting accurate courses in aviation and maritime navigation.
- Cryptography: Cryptography employs square roots in algorithms used for securing data transmission. For example, square roots are part of the calculations involved in generating public and private keys for encryption.
- Architecture: Architects use square roots to calculate areas and design elements. For instance, determining the amount of materials needed for a given area often requires squaring dimensions and taking square roots.
- Telecommunications: In wireless communication, the signal strength diminishes with the square of the distance from the transmitter. This inverse square law is critical for designing efficient communication networks.
These examples illustrate the versatility and importance of square roots in solving practical problems across a wide range of disciplines.
FAQs
-
Can a number have more than one square root?
Yes, every positive number has two square roots: a positive root (principal root) and a negative root. For example, the square roots of 16 are 4 and -4. The square root of 0 is a special case, having only one root, which is 0.
-
What is the square root of -1?
The square root of -1 is represented by the imaginary unit \(i\). Thus, the square roots of -1 are \(i\) and \(-i\).
-
How do I calculate the square root of a variable expression?
To find the square root of an expression with variables, you can follow these steps:
- Factor the expression into prime factors, including the variable factors.
- Take the square root by grouping the factors into pairs and taking one factor from each pair.
For example, to find the square root of \(64x^8\):
\[\sqrt{64x^8} = \sqrt{(2^6)(x^8)} = 2^3x^4 = 8x^4\]
-
What is a principal square root?
The principal square root of a number is the non-negative root. For example, the principal square root of 9 is 3, even though -3 is also a square root of 9.
-
How do I simplify a square root?
To simplify a square root, factor the number under the square root into its prime factors and then pair the factors. For each pair, take one factor out of the square root. For example:
\[\sqrt{72} = \sqrt{2^3 \cdot 3^2} = 3\sqrt{2^3} = 3\sqrt{8} = 6\sqrt{2}\]
-
How do I use a square root calculator?
Using a square root calculator is straightforward:
- Enter the number or expression whose square root you wish to find.
- Click the 'Calculate' button.
- The calculator will display the square root, both in simplified form (if applicable) and as a decimal approximation.
-
Why is calculating square roots important?
Square roots are essential in various fields such as algebra, geometry, and real-life applications including engineering, physics, and finance. They help in solving quadratic equations, finding distances, and calculating areas.
Conclusion
Understanding and calculating square roots with variables is a fundamental skill in algebra that extends to various applications in higher mathematics and real-world problems. Using a square root calculator simplifies the process, allowing for quick and accurate solutions, which is particularly useful when dealing with complex expressions.
Throughout this guide, we have explored the concept of square roots involving variables, discussed methods to calculate them, and highlighted the benefits of using a dedicated calculator for these tasks. We also provided practical examples and addressed common mistakes to avoid.
A square root with variables calculator can handle a wide range of expressions, from simple to complex, making it an invaluable tool for students, educators, and professionals. By ensuring you have a reliable calculator and a clear understanding of the underlying principles, you can confidently tackle mathematical challenges and enhance your problem-solving skills.
In summary, mastering square roots with variables not only bolsters your mathematical proficiency but also prepares you for more advanced topics and practical applications in fields such as engineering, physics, and economics. With practice and the right tools, you can achieve precision and efficiency in your calculations, paving the way for success in both academic and professional endeavors.
We hope this guide has provided you with a comprehensive understanding and practical insights into the world of square roots with variables. Keep exploring, practicing, and leveraging calculators to make your mathematical journey smoother and more enjoyable.
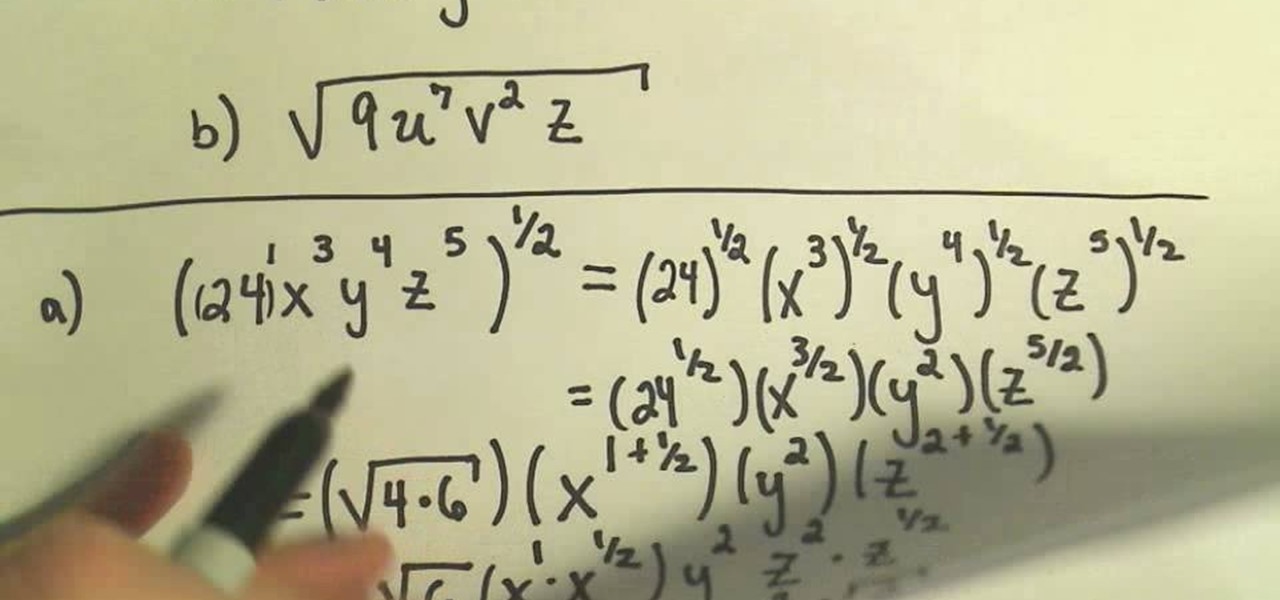
Video hướng dẫn cách đơn giản hóa căn bậc hai với biến số. Thích hợp cho học sinh và giáo viên muốn nâng cao kỹ năng toán học.
Căn Bậc Hai Với Biến Số (Đơn Giản Hóa Toán Học)
READ MORE:
Video hướng dẫn cách sử dụng máy tính để tính toán số mũ và căn bậc. Phù hợp cho học sinh, giáo viên và những người yêu thích toán học.
Máy Tính - Số Mũ & Căn Bậc (Rễ)