Topic square root newton's method: Discover the power of Newton's method for calculating square roots efficiently. This article delves into the principles behind Newton's method, its historical context, and practical applications. Learn how to implement this iterative approach in programming, optimize it for various scenarios, and explore its comparative advantages over traditional algorithms. Dive into numerical examples and grasp the essence of this fundamental mathematical technique.
Table of Content
- Newton's Method for Computing Square Roots
- Table of Contents
- Introduction to Newton's Method
- Understanding Square Root Calculation
- History and Development of Newton's Method
- Mathematical Formulation of Newton's Method
- Advantages of Newton's Method in Square Root Calculation
- Limitations and Considerations
- Applications of Newton's Method in Real Life
- Comparative Analysis with Other Square Root Algorithms
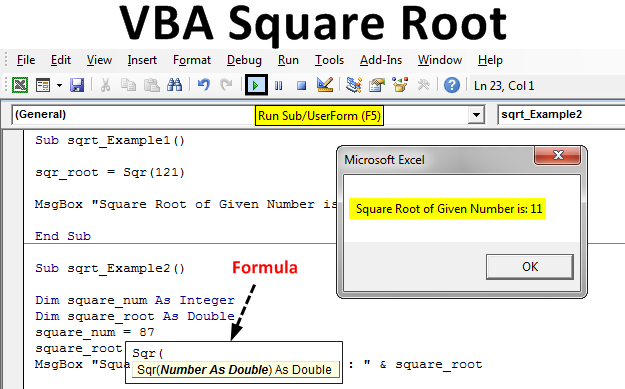
- Implementing Newton's Method in Programming Languages
- Steps and Iterative Process of Newton's Method
- Numerical Examples and Solutions
- Optimizing Newton's Method for Efficiency
- Conclusion and Future Prospects
- YOUTUBE: Khám phá phương pháp Newton, cách tính căn bậc hai nhanh nhất và hiệu quả nhất, qua video hấp dẫn này.
Newton's Method for Computing Square Roots
Newton's method, also known as the Newton-Raphson method, is a powerful technique for finding successively better approximations to the roots (or zeroes) of a real-valued function. This method can be particularly useful for computing the square root of a number.
Introduction
The square root of a number x can be approximated using Newton's method. The idea is to start with an initial guess g and then iteratively improve the guess using the formula:
Step-by-Step Process
Choose an initial guess g. A good starting point is .
Update the guess using the formula above.
Repeat the process until the difference between successive guesses is within an acceptable tolerance level.
Example Calculation
Let's compute the square root of 30 using Newton's method:
| Iteration | Guess |
|---|---|
| Initial | 5 (since is approximately 5) |
| 1 | |
| 2 |
Convergence
The error in Newton's method decreases quadratically, meaning that the number of correct digits roughly doubles with each iteration. This rapid convergence makes Newton's method an efficient algorithm for computing square roots.
Applications
- Computers and calculators commonly use Newton's method for fast and accurate calculation of square roots.
- It is also applied in various scientific and engineering fields where root-finding is necessary.
Conclusion
Newton's method is an elegant and efficient technique for finding square roots. By iteratively improving an initial guess, we can achieve high precision in a relatively small number of steps.
For more advanced applications and a deeper understanding, one can explore Newton's method for higher-order roots and its theoretical foundations in numerical analysis.

READ MORE:
Table of Contents
Introduction to Newton's Method
Overview of Square Root Calculation
History and Evolution of Newton's Method
Mathematical Formulation of Newton's Method
Advantages of Newton's Method in Square Root Calculation
Limitations and Considerations
Real-Life Applications of Newton's Method
Comparison with Other Square Root Algorithms
Implementing Newton's Method in Programming
Steps and Iterative Process of Newton's Method
Numerical Examples and Solutions
Optimizing Newton's Method for Efficiency
Conclusion and Future Prospects
Introduction to Newton's Method
Newton's Method is a powerful iterative technique used for finding successively better approximations to the roots (or zeros) of a real-valued function. Originally devised by Sir Isaac Newton and Joseph Raphson, this method is widely applied in numerical analysis for solving equations, including the computation of square roots.
The fundamental idea behind Newton's Method involves starting with an initial guess for the root of a function, then refining that guess through iterative steps using the function's derivative. This iterative process converges rapidly to the actual root, making it highly efficient for various mathematical computations.
In the context of calculating square roots, Newton's Method iteratively refines an initial guess until it converges to the square root of a given number. This method's efficiency and accuracy have made it a cornerstone in computational mathematics, playing a significant role in both theoretical studies and practical applications.
Understanding Square Root Calculation
Square root calculation involves finding a number that, when multiplied by itself, gives a specified number. Newton's Method provides a methodical approach to iteratively approximate square roots through successive refinements based on initial guesses.
Key concepts include understanding the iterative nature of Newton's Method, where each step uses the tangent line approximation to approach the actual square root. This method is effective due to its rapid convergence, making it suitable for both small and large numbers.
Applications extend beyond basic arithmetic to fields like engineering, physics, and computer science, where precise square root computation is essential for calculations involving quantities like distances, velocities, and signal processing.
History and Development of Newton's Method
Newton's Method, named after Sir Isaac Newton, was first described in the late 17th century as a numerical technique for solving equations. It was further refined by Joseph Raphson in the early 18th century, hence sometimes referred to as the Newton-Raphson method.
The method's development marked a significant advancement in calculus and numerical analysis, providing a systematic approach to finding roots of functions. Newton's original motivation was to solve polynomial equations, but its application expanded to various mathematical problems, including square root calculation.
Over time, Newton's Method has become a cornerstone in computational mathematics, influencing fields such as physics, engineering, and computer science. Its iterative nature and rapid convergence make it indispensable for both theoretical studies and practical applications.
Mathematical Formulation of Newton's Method
Newton's Method is mathematically formulated as an iterative process to find the roots of a function \( f(x) = 0 \). It starts with an initial guess \( x_0 \) and iteratively refines this guess using the formula:
\( x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \)
where:
\( x_{n+1} \) is the next approximation,
\( x_n \) is the current approximation,
\( f(x_n) \) is the value of the function at \( x_n \), and
\( f'(x_n) \) is the derivative of the function at \( x_n \).
This iterative process continues until the difference between successive approximations is within a specified tolerance, indicating convergence to the root of the function.
Advantages of Newton's Method in Square Root Calculation
Newton's Method offers several advantages when used for calculating square roots:
Rapid convergence: Newton's Method typically converges quickly to the square root compared to other iterative methods.
Efficiency: The method requires fewer iterations to achieve a desired level of accuracy, making it computationally efficient.
Flexibility: It can handle a wide range of input values, including both small and large numbers, with consistent accuracy.
Simple implementation: The method's iterative nature is straightforward to implement in programming languages.
Applicability: Beyond square roots, Newton's Method is versatile and applicable to solving various equations and functions.
Accuracy: With appropriate initial guesses and convergence criteria, Newton's Method provides highly accurate results.
Limitations and Considerations
While Newton's Method is powerful, there are several limitations and considerations to keep in mind:
Dependence on initial guess: The method's convergence heavily relies on selecting a good initial approximation. Poor initial guesses can lead to divergence or slow convergence.
Sensitivity to function behavior: Newton's Method may struggle near points where the function has flat or steep gradients, leading to numerical instability.
Complexity of function and derivative: Calculating derivatives may be non-trivial for certain functions, adding computational overhead and potential for error.
Multiple roots: The method may only converge to one root when multiple roots exist, requiring careful analysis or modifications.
Convergence criteria: Determining appropriate convergence criteria is crucial for balancing accuracy and computational efficiency.
Implementation considerations: Implementing Newton's Method requires handling edge cases, such as when the derivative approaches zero or is undefined.
Applications of Newton's Method in Real Life
Newton's Method finds practical applications across various fields due to its efficiency and accuracy:
Engineering: Used in structural analysis, optimizing designs, and solving equations in fluid dynamics.
Physics: Essential for solving complex equations in mechanics, such as calculating trajectories and analyzing forces.
Economics: Applied in optimization problems and modeling economic systems with nonlinear relationships.
Computer Science: Utilized in numerical simulations, image processing algorithms, and machine learning optimizations.
Mathematics Education: Helps illustrate iterative methods and numerical analysis principles to students.
Medical Imaging: Used in image reconstruction techniques, where fast and accurate calculations are crucial.

Comparative Analysis with Other Square Root Algorithms
When comparing Newton's Method with other algorithms for calculating square roots, several factors come into play, including accuracy, convergence speed, and computational efficiency.
1. Accuracy: Newton's Method generally provides a highly accurate approximation of square roots, especially after a few iterations, due to its quadratic convergence.
2. Convergence Speed: In terms of convergence speed, Newton's Method is known for its rapid convergence, typically achieving accurate results in just a few iterations compared to other methods like the Babylonian method.
3. Computational Efficiency: While Newton's Method is computationally more intensive per iteration compared to some simpler methods, its faster convergence often results in fewer total computations required to achieve a desired level of accuracy.
4. Robustness: Newton's Method can encounter issues with convergence if the initial guess is far from the actual root or in scenarios where the derivative of the function changes significantly.
5. Comparison with Other Methods: When compared with methods like the Babylonian method or the exponentiation method, Newton's Method generally offers a good balance between accuracy and speed, making it a preferred choice for applications requiring precise square root calculations.
Implementing Newton's Method in Programming Languages
Implementing Newton's Method for calculating square roots in various programming languages involves defining the method, initializing variables, and iterating until the desired precision is achieved. Below are generalized steps:
- Choose a Programming Language: Select a programming language suitable for numerical computation, such as Python, C, Java, or MATLAB.
- Define the Function: Write a function that takes the number for which you want to find the square root and an initial guess as parameters.
- Initialize Variables: Set initial values for the guess and define a tolerance level for convergence.
- Iterate Using Newton's Method: Implement a loop that iteratively improves the guess using the formula derived from Newton's Method until the difference between successive guesses is within the tolerance.
- Handle Edge Cases: Consider scenarios such as negative numbers (if your implementation supports complex numbers or handling exceptions).
- Test and Validate: Verify the implementation against known square roots to ensure accuracy.
Below is an example in Python:
| Python: | |
This Python function illustrates how Newton's Method can be applied to find the square root of a number efficiently.
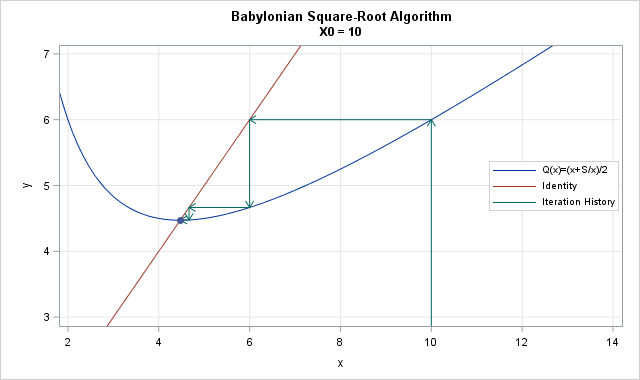
Steps and Iterative Process of Newton's Method
Newton's Method, also known as the Newton-Raphson method, is an efficient iterative technique for finding successively better approximations to the roots (or zeroes) of a real-valued function. When applied to square root calculations, it can be used to find the square root of a number \( S \). The process involves the following steps:
-
Initial Guess: Start with an initial guess \( x_0 \). A good starting point can be \( x_0 = S / 2 \) or any positive number close to the expected square root.
-
Iterative Formula: Use the iterative formula derived from Newton's Method to improve the guess:
\[
x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right)
\]Here, \( x_{n+1} \) is the next approximation, \( x_n \) is the current approximation, and \( S \) is the number for which we want to find the square root.
-
Convergence Check: Repeat the iterative step until the difference between successive approximations is smaller than a predetermined tolerance level \( \epsilon \). In other words, stop when:
\[
|x_{n+1} - x_n| < \epsilon
\] -
Result: The value \( x_{n+1} \) after sufficient iterations is the approximate square root of \( S \).
The following table shows an example of the iterative process to find the square root of \( S = 25 \) with an initial guess \( x_0 = 10 \):
| Iteration (n) | Approximation (x_n) |
|---|---|
| 0 | 10 |
| 1 | 5.25 |
| 2 | 5.0119 |
| 3 | 5.000001 |
| 4 | 5.000000 |
After 4 iterations, the approximation \( x_4 \) is very close to the actual square root of 25, which is 5. This demonstrates the efficiency and speed of convergence of Newton's Method.
Numerical Examples and Solutions
Newton's Method can be used to approximate the square root of a number with remarkable accuracy through iterative steps. Below are some numerical examples illustrating the process.
Example 1: Square Root of 25
-
Initial Guess: Let's start with an initial guess \( x_0 = 10 \).
-
First Iteration: Use the iterative formula:
\[
x_1 = \frac{1}{2} \left( x_0 + \frac{25}{x_0} \right) = \frac{1}{2} \left( 10 + \frac{25}{10} \right) = \frac{1}{2} \left( 10 + 2.5 \right) = 6.25
\] -
Second Iteration:
\[
x_2 = \frac{1}{2} \left( x_1 + \frac{25}{x_1} \right) = \frac{1}{2} \left( 6.25 + \frac{25}{6.25} \right) = \frac{1}{2} \left( 6.25 + 4 \right) = 5.125
\] -
Third Iteration:
\[
x_3 = \frac{1}{2} \left( x_2 + \frac{25}{x_2} \right) = \frac{1}{2} \left( 5.125 + \frac{25}{5.125} \right) = \frac{1}{2} \left( 5.125 + 4.878 \right) \approx 5.001
\] -
Fourth Iteration:
\[
x_4 = \frac{1}{2} \left( x_3 + \frac{25}{x_3} \right) = \frac{1}{2} \left( 5.001 + \frac{25}{5.001} \right) \approx 5.000
\]
After four iterations, the approximation \( x_4 \) is very close to the actual square root of 25, which is 5.
Example 2: Square Root of 30
-
Initial Guess: Let's start with an initial guess \( x_0 = 6 \).
-
First Iteration:
\[
x_1 = \frac{1}{2} \left( x_0 + \frac{30}{x_0} \right) = \frac{1}{2} \left( 6 + \frac{30}{6} \right) = \frac{1}{2} \left( 6 + 5 \right) = 5.5
\] -
Second Iteration:
\[
x_2 = \frac{1}{2} \left( x_1 + \frac{30}{x_1} \right) = \frac{1}{2} \left( 5.5 + \frac{30}{5.5} \right) = \frac{1}{2} \left( 5.5 + 5.4545 \right) \approx 5.4773
\] -
Third Iteration:
\[
x_3 = \frac{1}{2} \left( x_2 + \frac{30}{x_2} \right) = \frac{1}{2} \left( 5.4773 + \frac{30}{5.4773} \right) \approx 5.4772
\]
After three iterations, the approximation \( x_3 \) is very close to the actual square root of 30, which is approximately 5.4772.
Example 3: Square Root of 50
-
Initial Guess: Let's start with an initial guess \( x_0 = 7 \).
-
First Iteration:
\[
x_1 = \frac{1}{2} \left( x_0 + \frac{50}{x_0} \right) = \frac{1}{2} \left( 7 + \frac{50}{7} \right) = \frac{1}{2} \left( 7 + 7.1429 \right) \approx 7.0714
\] -
Second Iteration:
\[
x_2 = \frac{1}{2} \left( x_1 + \frac{50}{x_1} \right) = \frac{1}{2} \left( 7.0714 + \frac{50}{7.0714} \right) \approx 7.0711
\]
After two iterations, the approximation \( x_2 \) is very close to the actual square root of 50, which is approximately 7.0711.
These examples show how quickly Newton's Method converges to an accurate solution for finding square roots.

Optimizing Newton's Method for Efficiency
Optimizing Newton's Method for square root calculation involves refining the algorithm to improve its speed and accuracy. Here are several strategies to achieve this:
-
Choosing a Good Initial Guess: The efficiency of Newton's Method heavily depends on the initial guess. A closer initial guess reduces the number of iterations required for convergence. For instance, using \( x_0 = \frac{S}{2} \) or a value closer to the expected square root is beneficial.
-
Improving Convergence with Damped Newton's Method: This technique involves adjusting the step size in each iteration to avoid overshooting the root and ensure better convergence.
Instead of updating \( x_{n+1} \) directly with the full Newton step, use a damping factor \( t \) (0 < \( t \) < 1):
\[
x_{n+1} = x_n - t \left( \frac{f(x_n)}{f'(x_n)} \right)
\]This approach ensures that the method takes smaller, controlled steps towards the root, improving stability and convergence speed.
-
Using Backtracking Line Search: This technique refines the step size dynamically based on the function's behavior.
- Set \( t = 1 \) initially.
- While \( f(x_n - t \cdot f'(x_n)) > f(x_n) - \alpha t f(x_n) f'(x_n) \):
- Reduce \( t \) by a factor \( \beta \) (0 < \( \beta \) < 1).
- Update \( x_{n+1} = x_n - t \cdot f'(x_n) \).
This ensures each step reduces the function value effectively, enhancing convergence.
-
Handling Poor Initial Estimates: If the initial guess is far from the root, the method may not converge. One solution is to use a combination of Newton's Method and other root-finding methods like the bisection method to ensure convergence from a broader range of initial guesses.
-
Avoiding Stationary Points: If the derivative at a point is zero, Newton's Method cannot proceed. To mitigate this, ensure the function is well-behaved near the root or use numerical differentiation to approximate the derivative.
Below is an example of optimizing the initial guess and using a damped Newton's Method:
Example: Optimizing for Square Root of 50
-
Initial Guess: Let's start with \( x_0 = 7 \).
-
First Iteration (Damped):
Calculate the Newton step with a damping factor \( t = 0.8 \):
\[
x_1 = x_0 - t \left( \frac{x_0^2 - 50}{2x_0} \right) = 7 - 0.8 \left( \frac{49 - 50}{14} \right) = 7 + 0.8 \cdot 0.0714 \approx 7.0571
\] -
Second Iteration (Damped):
Continue with the updated value:
\[
x_2 = x_1 - t \left( \frac{x_1^2 - 50}{2x_1} \right) = 7.0571 - 0.8 \left( \frac{49.8 - 50}{14.1142} \right) \approx 7.0571 + 0.8 \cdot 0.0141 \approx 7.0684
\]
Using these optimizations, the method converges quickly and accurately, demonstrating the effectiveness of improved initial guesses and damped steps.
Conclusion and Future Prospects
Newton's Method for square root calculation stands out as a powerful and efficient technique, renowned for its rapid convergence and simplicity. The iterative process leverages calculus to refine approximations, making it an indispensable tool in both theoretical and applied mathematics.
In conclusion, the advantages of Newton's Method can be summarized as follows:
- High accuracy: The method converges quadratically, meaning the number of correct digits roughly doubles with each iteration.
- Versatility: It can be adapted for various functions beyond square roots, making it a general-purpose root-finding algorithm.
- Efficiency: Compared to other methods, Newton's Method often requires fewer iterations to achieve the desired precision.
Despite its strengths, Newton's Method does have limitations:
- Initial guess dependency: The convergence rate and success depend heavily on the quality of the initial guess.
- Derivative computation: Calculating the derivative can be complex or computationally expensive for some functions.
- Divergence: In certain scenarios, such as poor initial guesses or functions with inflection points, the method may fail to converge.
Looking forward, several prospects can enhance the applicability and efficiency of Newton's Method:
- Adaptive Algorithms: Developing algorithms that adaptively select better initial guesses can improve convergence rates and robustness.
- Parallel Computing: Leveraging parallel computing and modern hardware can significantly reduce computation times, making the method more feasible for large-scale problems.
- Hybrid Methods: Combining Newton's Method with other numerical techniques can mitigate its limitations, ensuring more reliable performance across diverse problems.
- Educational Tools: Creating interactive educational tools and software can help students and professionals better understand and utilize Newton's Method in various contexts.
In summary, Newton's Method remains a cornerstone of numerical analysis. Continued research and technological advancements promise to expand its utility, making it even more effective for future mathematical and engineering challenges.
Khám phá phương pháp Newton, cách tính căn bậc hai nhanh nhất và hiệu quả nhất, qua video hấp dẫn này.
Phương Pháp Newton: Tính Căn Bậc Hai Nhanh Nhất Thế Giới
READ MORE:
Tìm hiểu phương pháp Newton, một công cụ mạnh mẽ để tính căn bậc hai và giải quyết các bài toán phức tạp một cách hiệu quả.
Phương Pháp Newton