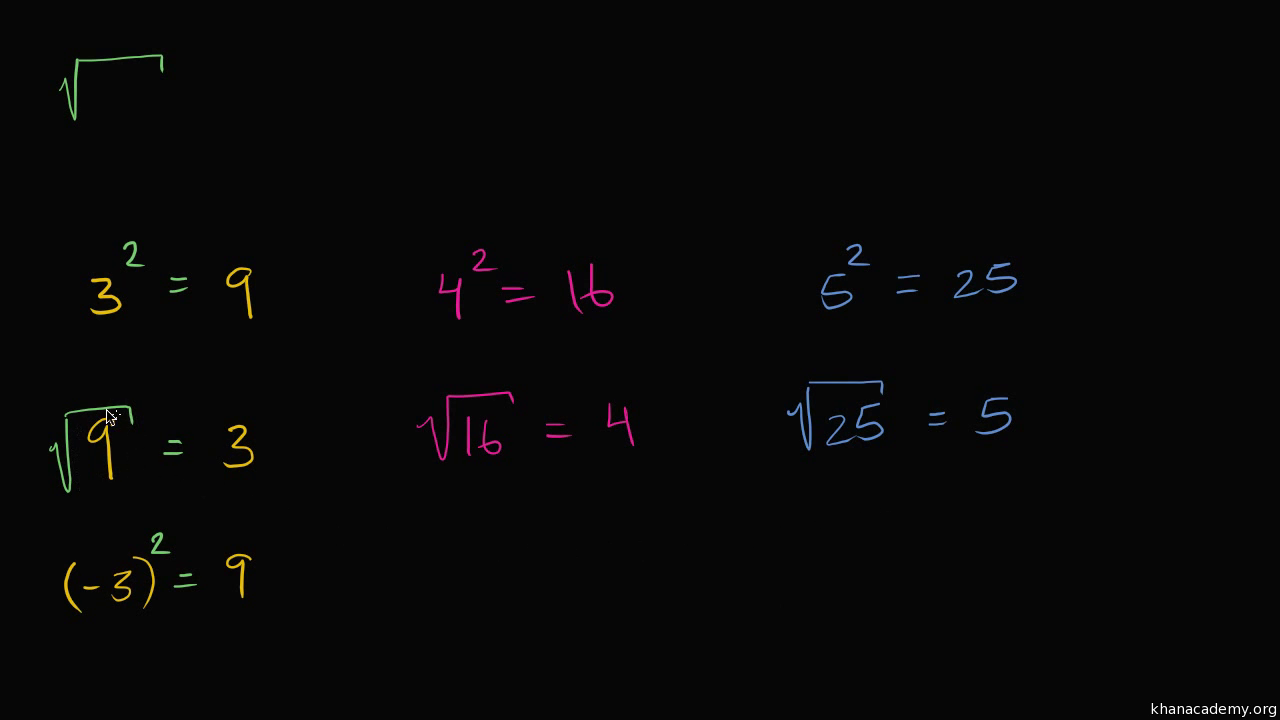Topic square root division calculator: Discover the simplicity of using a Square Root Division Calculator to solve complex mathematical problems efficiently. Whether you're a student or a professional, this tool helps you divide square roots accurately with step-by-step instructions, making your calculations faster and more reliable.
Table of Content
- Square Root Division Calculator
- Introduction
- Understanding Square Roots
- Basic Square Root Calculations
- Square Root Division
- Simplifying Square Roots
- Complex and Negative Square Roots
- Square Root of Fractions
- Perfect Squares and Their Properties
- Applications of Square Roots in Mathematics
- Step-by-Step Use of a Square Root Calculator
- Practice Problems and Examples
- Additional Resources and References
- YOUTUBE: Hướng dẫn sử dụng máy tính khoa học để tính căn bậc hai một cách đơn giản và chính xác.
Square Root Division Calculator
A square root division calculator is a tool designed to perform calculations involving square roots and divisions efficiently. Below is an overview of the functionalities, methods, and usage of such a calculator.
Functionalities
- Calculate the square root of any given number.
- Divide square roots.
- Handle complex numbers and fractions.
- Provide step-by-step solutions.
- Determine whether a number has a perfect square root.
Methods for Calculating Square Roots
- Estimation Method
- Long Division Method
Square Root Formula
The basic formula for calculating the square root is:
\[ \sqrt{x} \]
For dividing square roots, the formula is:
\[ \frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} \]
Examples
Let's consider a few examples to understand how the calculator works:
- Example 1: Calculate the square root of 64.
- Using the Prime Factorization Method:
- Example 2: Calculate the square root of 25.
- Example 3: Calculate the square root of a fraction \(\frac{9}{25}\).
\[ 64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 = (2 \times 2 \times 2)^2 = 8^2 \]
\[ \sqrt{64} = 8 \]
\[ 25 = 5 \times 5 = 5^2 \]
\[ \sqrt{25} = 5 \]
\[ \sqrt{\frac{9}{25}} = \frac{\sqrt{9}}{\sqrt{25}} = \frac{3}{5} = 0.6 \]
Square Root of Negative Numbers
To find the square root of negative numbers, we use complex numbers:
\[ i = \sqrt{-1} \]
Example:
\[ \sqrt{-4} = \sqrt{-1 \times 4} = \sqrt{-1} \times \sqrt{4} = 2i \]
How to Use the Calculator
- Select the type of root (square root or nth root).
- Enter the number for which you want to calculate the square root.
- Click on the 'Calculate' button.
- View the results, which include the square root, step-by-step calculation, and whether the number has a perfect square root.
Frequently Asked Questions (FAQs)
- Can a number have more than one square root? Yes, positive numbers have both a positive and a negative square root.
- Is \(\sqrt{2}\) a rational number? No, \(\sqrt{2}\) is an irrational number as it cannot be expressed as the quotient of two integers.
- Are all square roots rational? Some are rational while others are irrational.
- How can I find the square root without a calculator? You can use methods such as estimation, long division, and prime factorization.
Square Root Table – Perfect Squares
| x | \(\sqrt{x}\) |
| 1 | 1 |
| 2 | 1.41421 |
| 3 | 1.73205 |
| 4 | 2 |
| 5 | 2.23607 |

READ MORE:
Introduction
Welcome to the Comprehensive Guide to Square Root Division Calculators. This guide is designed to provide you with a thorough understanding of square root division and the tools available to simplify these calculations. Whether you're a student, teacher, or math enthusiast, this guide will help you navigate through the complexities of square roots and their division.
Square roots are fundamental in mathematics, representing the value that, when multiplied by itself, gives the original number. The concept of dividing square roots can be challenging, but with the right tools and knowledge, it becomes manageable and even enjoyable.
This guide will cover a variety of topics, including basic square root calculations, simplifying square roots, and dealing with complex and negative square roots. Additionally, we'll explore the practical applications of square roots in mathematics and provide step-by-step instructions for using a square root division calculator.
Here's what you can expect to find in this guide:
- An overview of square roots and their properties
- Detailed explanations of square root division
- Techniques for simplifying square roots
- Handling complex and negative square roots
- Understanding the square root of fractions
- Identifying perfect squares and their characteristics
- Practical applications of square roots in various fields
- A step-by-step tutorial on using a square root calculator
- Practice problems and examples to reinforce your learning
- Frequently asked questions and additional resources
By the end of this guide, you'll have a solid grasp of square root division and the confidence to tackle these calculations with ease. Let's dive into the world of square roots and discover the simplicity behind the complexity.
Understanding Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3, because 3 * 3 = 9. Square roots are a fundamental concept in mathematics, frequently used in various calculations and problem-solving scenarios.
To denote the square root of a number, we use the radical symbol (√). For instance, the square root of x is represented as √x.
Here are some basic properties and rules of square roots:
- Non-negative numbers: The square root of a non-negative number is also non-negative. For example, √16 = 4.
- Product property: √(a * b) = √a * √b. For example, √(4 * 9) = √4 * √9 = 2 * 3 = 6.
- Quotient property: √(a / b) = √a / √b. For example, √(25 / 4) = √25 / √4 = 5 / 2 = 2.5.
- Perfect squares: A perfect square is a number that has an integer as its square root. For instance, 36 is a perfect square because its square root is 6.
Square roots are not always whole numbers. When the square root of a number is not an integer, it is called an irrational number. For example, √2 is approximately 1.414 and cannot be expressed exactly as a fraction.
Square roots also play a significant role in solving equations and in geometry. They are used to find distances, areas, and in various algebraic formulas. Understanding how to manipulate and simplify square roots is crucial for solving complex mathematical problems.
Here is a simple example:
Calculate the square root of 49.
- Identify the number to be rooted: 49.
- Since 49 is a perfect square, find the integer whose square is 49: 7 * 7 = 49.
- Thus, the square root of 49 is 7, so √49 = 7.
Using these fundamental concepts, you can effectively work with square roots in various mathematical contexts. For more complex calculations, online square root calculators can provide step-by-step solutions, simplifying the process and ensuring accuracy.
Basic Square Root Calculations
Understanding basic square root calculations is fundamental to mastering more complex mathematical concepts. The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because \(3 \times 3 = 9\).
Key Properties of Square Roots
- The square root of a positive number is always positive.
- Every positive number has two square roots: a positive and a negative root. For instance, both \(3\) and \(-3\) are square roots of \(9\).
- The square root of \(0\) is \(0\).
- There is no real square root of a negative number (the square roots are imaginary numbers).
Calculating Square Roots
There are different methods to calculate square roots:
- Using a calculator:
- Enter the number for which you want to find the square root.
- Press the square root (√) button.
- Read the result.
- Manual calculation:
- Estimate a number.
- Square the estimate and compare it to the original number.
- Adjust the estimate and repeat until the desired accuracy is achieved.
Examples
Here are some examples of basic square root calculations:
- \(\sqrt{25} = 5\)
- \(\sqrt{100} = 10\)
- \(\sqrt{2} \approx 1.414\)
Using MathJax for Square Root Calculations
MathJax can help in displaying square root calculations clearly. Here’s how to use it:
For a simple square root: \(\sqrt{n}\) where \(n\) is the number.
For example, to display the square root of 16, you would write: \(\sqrt{16}\) which renders as \(\sqrt{16}\).
Basic understanding of these principles and methods will help you effectively use square root calculators and perform manual calculations when needed.
Square Root Division
Dividing square roots involves a few straightforward steps. The key is to remember some basic rules about radicals, which allow us to simplify and manipulate these expressions effectively.
Basic Rule
The fundamental rule for dividing square roots is:
\[\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\]
This rule states that the quotient of two square roots is the square root of the quotient of the numbers.
Step-by-Step Process
- Write down the division of the square roots: \(\frac{\sqrt{a}}{\sqrt{b}}\).
- Apply the basic rule to combine the square roots under a single radical: \(\sqrt{\frac{a}{b}}\).
- Simplify the fraction under the square root if possible.
- If the fraction under the square root can be simplified further, factorize it into its prime factors and then simplify the square root.
Example Calculation
Let's consider an example: \(\frac{\sqrt{50}}{\sqrt{2}}\).
- Combine the square roots: \(\sqrt{\frac{50}{2}}\).
- Simplify the fraction: \(\sqrt{25}\).
- Find the square root of 25: \(5\).
Thus, \(\frac{\sqrt{50}}{\sqrt{2}} = 5\).
Handling More Complex Expressions
For more complex expressions, you might need to factorize the numbers inside the square root. For instance, dividing \(\frac{5\sqrt{30}}{2\sqrt{10}}\) involves the following steps:
- Combine the square roots: \(\frac{5\sqrt{30}}{2\sqrt{10}} = \frac{5}{2} \cdot \sqrt{\frac{30}{10}}\).
- Simplify the fraction under the square root: \(\sqrt{3}\).
- Combine the constants: \(\frac{5}{2} \cdot \sqrt{3} = 2.5\sqrt{3}\).
Using a Calculator
Square root division calculators can simplify this process significantly by providing step-by-step solutions. These calculators allow you to input the expressions and see the detailed process of combining and simplifying the radicals.
For instance, using a square root calculator, you can input \(\frac{\sqrt{75}}{\sqrt{3}}\) and the calculator will show:
- Combine the square roots: \(\sqrt{\frac{75}{3}} = \sqrt{25}\).
- Find the square root of 25: \(5\).
Therefore, \(\frac{\sqrt{75}}{\sqrt{3}} = 5\).
Conclusion
Dividing square roots becomes simple once you understand the basic rule and practice a few examples. Using a calculator can also help verify your work and ensure accuracy.

Simplifying Square Roots
Simplifying square roots involves expressing the square root in its simplest form. This means breaking down the number inside the square root into its prime factors and pulling out pairs of identical factors.
Steps to Simplify a Square Root
- Factorize the Radicand:
Begin by breaking down the number inside the square root (radicand) into its prime factors.
Example: \( \sqrt{72} \)
\( 72 = 2 \times 36 = 2 \times 6 \times 6 = 2 \times 2 \times 3 \times 3 \times 2 \)
- Group the Factors:
Group the factors into pairs of identical factors.
Example: \( \sqrt{72} = \sqrt{2^2 \times 3^2 \times 2} \)
- Extract the Pairs:
Take one number from each pair out of the square root.
Example: \( \sqrt{2^2 \times 3^2 \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \)
Examples
- \( \sqrt{50} \)
Prime factorization: \( 50 = 2 \times 25 = 2 \times 5 \times 5 \)
Group factors: \( \sqrt{50} = \sqrt{2 \times 5^2} \)
Extract pairs: \( \sqrt{2 \times 5^2} = 5\sqrt{2} \)
- \( \sqrt{200} \)
Prime factorization: \( 200 = 2^3 \times 5^2 \)
Group factors: \( \sqrt{200} = \sqrt{2^3 \times 5^2} = \sqrt{2^2 \times 2 \times 5^2} \)
Extract pairs: \( \sqrt{2^2 \times 2 \times 5^2} = 2 \times 5 \sqrt{2} = 10\sqrt{2} \)
Fractions
Simplifying square roots of fractions follows a similar method.
- \( \sqrt{\frac{4}{9}} \)
\( \sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}} = \frac{2}{3} \)
Why Simplify Square Roots?
Simplifying square roots makes them easier to work with in mathematical equations and helps in solving algebraic expressions more efficiently.
Complex and Negative Square Roots
Square roots of negative and complex numbers can be challenging, but understanding the basic principles makes it easier. Here's a step-by-step guide:
Square Roots of Negative Numbers
To find the square root of a negative number, we use the imaginary unit \( i \), where \( i = \sqrt{-1} \). This transforms the problem into one involving complex numbers.
For example, the square root of -4 is:
\[
\sqrt{-4} = \sqrt{4 \cdot (-1)} = \sqrt{4} \cdot \sqrt{-1} = 2i
\]
Square Roots of Complex Numbers
Finding the square root of a complex number such as \( z = a + bi \) involves converting the number into polar form. The polar form of a complex number is \( z = r(\cos \theta + i \sin \theta) \), where \( r \) is the modulus and \( \theta \) is the argument.
Here’s how to find the square root:
- Calculate the modulus \( r \): \[ r = \sqrt{a^2 + b^2} \]
- Determine the argument \( \theta \): \[ \theta = \tan^{-1} \left( \frac{b}{a} \right) \]
- Use the polar form to find the square roots: \[ \sqrt{z} = \pm \sqrt{r} \left( \cos \frac{\theta}{2} + i \sin \frac{\theta}{2} \right) \]
For example, to find the square roots of \( 3 + 4i \):
- Calculate the modulus: \[ r = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
- Determine the argument: \[ \theta = \tan^{-1} \left( \frac{4}{3} \right) \]
- Use the polar form to find the square roots: \[ \sqrt{3 + 4i} = \pm \sqrt{5} \left( \cos \frac{\theta}{2} + i \sin \frac{\theta}{2} \right) \]
Practice Example
Let's simplify \( \sqrt{-9} \):
\[
\sqrt{-9} = \sqrt{9 \cdot (-1)} = \sqrt{9} \cdot \sqrt{-1} = 3i
\]
To simplify \( \sqrt{5 - 12i} \), follow the steps outlined above for complex numbers.
Conclusion
Understanding how to handle square roots of negative and complex numbers opens up a new world in mathematics. Using the imaginary unit \( i \) and converting complex numbers to polar form are essential techniques in this process.
Square Root of Fractions
Finding the square root of a fraction involves a straightforward process that can be broken down into simple steps. The square root of a fraction is calculated by taking the square root of the numerator and the square root of the denominator separately.
- Start with the fraction in the form
x/y, wherexis the numerator andyis the denominator. - Find the square root of the numerator (
√x). - Find the square root of the denominator (
√y). - Combine the results to get
√(x/y) = √x / √y.
For example, let's find the square root of the fraction 4/16:
√(4/16) = √4 / √16
√4 = 2
√16 = 4
√(4/16) = 2 / 4 = 1/2
Therefore, the square root of the fraction 4/16 is 1/2 or 0.5.
In some cases, it is preferable to avoid leaving a square root in the denominator. This can be done by rationalizing the denominator:
- Multiply both the numerator and the denominator by the same number to remove the square root from the denominator.
For example, to rationalize the square root of the fraction 1/√2:
1/√2 × √2/√2 = √2/2
Here are some additional examples:
√(9/25) = √9 / √25 = 3 / 5 = 0.6√(20/36) = √20 / √36 = 4.47 / 6 = 0.745
Using a square root fraction calculator can simplify these computations, especially for more complex fractions. Simply input the numerator and denominator into the calculator, and it will quickly provide the square root.
Perfect Squares and Their Properties
A perfect square is a number that can be expressed as the product of an integer with itself. In other words, it is the square of an integer. Understanding perfect squares is fundamental in mathematics and has various applications in calculations and problem-solving.
Key properties of perfect squares include:
- Definition: A perfect square is represented as \( n^2 \), where \( n \) is an integer.
- Examples: Examples of perfect squares are 1, 4, 9, 16, 25, etc.
- Non-negative Results: The square of any integer is non-negative.
- Even or Odd: A perfect square is either even or odd, depending on whether the integer \( n \) is even or odd.
- Roots and Divisibility: The square root of a perfect square is always an integer, and perfect squares are divisible by their square roots without remainder.
Understanding these properties is crucial when dealing with calculations involving square roots, as they simplify the process of verification and manipulation of square root division. Applications range from basic arithmetic to advanced mathematics and physics, where perfect squares play a significant role in modeling and problem-solving.

Applications of Square Roots in Mathematics
Square roots find numerous applications across various branches of mathematics, contributing to both theoretical developments and practical problem-solving. Some key applications include:
- Geometry: In geometry, square roots are used to calculate distances, such as the length of a diagonal in a square or the radius of a circle from its area.
- Algebra: Square roots are essential in solving quadratic equations and inequalities, where they help determine the roots of polynomials.
- Physics: In physics, square roots are integral to formulas involving acceleration, force, and energy, providing insights into natural phenomena.
- Finance: Square roots are used in finance to calculate the standard deviation of returns and risk assessments in investment portfolios.
- Computer Science: Algorithms in computer science utilize square roots for tasks such as optimizing data structures and implementing cryptographic functions.
- Engineering: Engineers rely on square roots for designing structures, analyzing vibrations, and determining electrical and mechanical properties.
- Statistics: In statistics, square roots are employed to compute measures of dispersion, such as the root mean square deviation and variance.
Understanding the applications of square roots enhances problem-solving capabilities across disciplines, making it a fundamental concept in both academic and practical contexts.
Step-by-Step Use of a Square Root Calculator
Using a square root calculator can simplify the process of finding square roots, especially for complex or large numbers. Here’s a step-by-step guide:
- Enter Number: Input the number for which you want to find the square root into the calculator.
- Select Calculation Method: Depending on the calculator, choose the method to compute the square root (e.g., standard square root or simplified form).
- Execute Calculation: Click or press the appropriate button to perform the calculation.
- Review Result: The calculator will display the square root of the entered number.
- Verify Accuracy: If needed, verify the accuracy of the result by squaring the calculated square root to ensure it matches the original number.
Modern square root calculators can handle various types of inputs, including fractions, decimals, and even complex numbers. They are valuable tools for both students learning about square roots and professionals needing quick and precise calculations.
Practice Problems and Examples
Practice problems and examples help reinforce understanding and application of square root division concepts. Here are some illustrative examples:
-
Example 1: Calculate \( \sqrt{144} \).
- Input: \( 144 \)
- Calculation: \( \sqrt{144} = 12 \)
- Result: \( \sqrt{144} = 12 \)
-
Example 2: Determine \( \sqrt{2} \) to three decimal places.
- Input: \( 2 \)
- Calculation: \( \sqrt{2} \approx 1.414 \)
- Result: \( \sqrt{2} \approx 1.414 \)
-
Example 3: Simplify \( \sqrt{27} \).
- Input: \( 27 \)
- Prime Factorization: \( 27 = 3^3 \)
- Simplify: \( \sqrt{27} = \sqrt{3^3} = 3\sqrt{3} \)
- Result: \( \sqrt{27} = 3\sqrt{3} \)
Practice problems and examples like these help develop proficiency in handling different types of square root division scenarios, from basic calculations to more complex simplifications and approximations.
Additional Resources and References
Explore further resources and references to deepen your understanding of square root division:
- that cover square roots and division concepts extensively.
- Online offering courses on algebra and advanced mathematics.
- Scientific discussing applications of square roots in various disciplines.
- and calculators for precise calculations involving square roots.
- Community where experts and learners share insights and solutions related to square root division.
These resources can provide valuable information, explanations, and practical examples to enhance your knowledge and skills in using square root division effectively.

Hướng dẫn sử dụng máy tính khoa học để tính căn bậc hai một cách đơn giản và chính xác.
Hướng dẫn máy tính 9: Các căn bậc hai trên máy tính khoa học
READ MORE:
Hướng dẫn cách xấp xỉ căn bậc hai của một số một cách đơn giản và hiệu quả, phù hợp cho những người muốn tính toán căn bậc hai mà không cần sử dụng máy tính.
Cách ước tính căn bậc hai của một số