Topic 80 square rooted: Understanding the square root of 80 is essential for various mathematical and real-world applications. In this article, we explore the value, properties, and practical uses of 80 square rooted. Dive into simplified forms, decimal representations, and fascinating facts that make this number both intriguing and useful.
Table of Content
- Square Root of 80
- Introduction to Square Roots
- Understanding the Square Root of 80
- Decimal Representation of the Square Root of 80
- Simplifying the Square Root of 80
- Properties of the Square Root of 80
- Prime Factorization and Perfect Square Factors
- Positive and Negative Square Roots
- Applications of the Square Root of 80
- Calculating Square Roots Using Different Methods
- Real-World Examples Involving the Square Root of 80
- Visualizing the Square Root of 80
- Frequently Asked Questions
- Conclusion
- YOUTUBE: Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai của 80. Video này giúp bạn hiểu rõ hơn về cách tính toán và ứng dụng căn bậc hai của 80.
Square Root of 80
The square root of a number is a value that, when multiplied by itself, gives the original number. The square root of 80 can be expressed as:
or
Decimal Form
The square root of 80 in decimal form is approximately:
Simplified Radical Form
The square root of 80 can also be simplified to its radical form:
Properties
- Prime Factorization: The prime factors of 80 are 2 and 5.
- Perfect Square Factors: 16 is the largest perfect square factor of 80.
- Positive and Negative Roots: The square root of 80 has both a positive and negative value: .
Applications
Understanding the square root of 80 is useful in various fields such as engineering, physics, and mathematics. It is often needed in problems involving area, volume, and the Pythagorean theorem.
READ MORE:
Introduction to Square Roots
Square roots are fundamental concepts in mathematics, representing a value that, when multiplied by itself, yields the original number. The square root of a number is denoted as or .
Here is a step-by-step guide to understanding square roots:
- Definition: The square root of a number is a value that, when multiplied by itself, gives the original number.
- Notation: The square root is represented by the radical symbol . For example, the square root of 80 is written as .
- Positive and Negative Roots: Every positive number has two square roots: a positive and a negative. For example, equals approximately 8.944 and -8.944.
- Perfect Squares: Numbers like 1, 4, 9, 16, 25 are perfect squares because their square roots are integers (1, 2, 3, 4, 5 respectively).
- Non-Perfect Squares: Numbers that are not perfect squares have irrational square roots, which cannot be expressed as exact fractions. For example, is approximately 8.94427, which is an irrational number.
- Calculation Methods:
- Prime Factorization: Breaking down the number into its prime factors can simplify the square root. For example, can be factored into , leading to .
- Estimation: Approximating the square root through methods like the Babylonian method (iterative averaging).
- Calculators: Modern calculators provide quick and accurate square root calculations.
Square roots are widely used in various fields such as algebra, geometry, engineering, and physics, making them a crucial part of mathematical education and application.
Understanding the Square Root of 80
The square root of 80 is a value that, when multiplied by itself, equals 80. This can be represented mathematically as:
To better understand the square root of 80, let's break it down step-by-step:
- Prime Factorization:
First, we factor 80 into its prime components:
- Simplifying the Radical:
We can simplify the square root of 80 by grouping the prime factors into pairs:
- Decimal Form:
The decimal approximation of the square root of 80 is:
- Properties:
- Positive and Negative Roots: The square root of 80 includes both a positive and negative value:
- Non-Perfect Square: 80 is not a perfect square, which means its square root is an irrational number.
- Applications: The square root of 80 is used in various mathematical and real-world applications, including geometry and physics.
- Positive and Negative Roots: The square root of 80 includes both a positive and negative value:
Understanding the square root of 80 involves breaking down the number into its prime factors, simplifying the radical, and appreciating its decimal form and properties. This knowledge is useful for solving problems in algebra, geometry, and other mathematical fields.
Decimal Representation of the Square Root of 80
The decimal representation of the square root of 80 provides a precise numerical value that is easy to use in calculations. Here’s how we can determine and understand this value step by step:
- Calculating the Square Root:
The square root of 80 can be calculated using a calculator or mathematical algorithms, resulting in:
- Understanding the Decimal Places:
The value is an approximation that can be extended to more decimal places for greater precision:
- To two decimal places:
- To three decimal places:
- To five decimal places:
- Significance in Calculations:
Using the decimal form of the square root of 80 is crucial in various fields:
- Engineering: Precise measurements and calculations often require the square root of 80 in decimal form.
- Physics: Many physical formulas and constants involve square roots, necessitating accurate decimal values.
- Mathematics: Solving equations and performing numerical analysis can be more manageable with decimal approximations.
- Comparison with Other Square Roots:
For context, it’s helpful to compare the square root of 80 with other nearby square roots:
Number Square Root (Approx.) 64 8 81 9 100 10
Understanding the decimal representation of the square root of 80 is fundamental for precise calculations in various scientific and mathematical applications. The value is a practical approximation used in many contexts.
Simplifying the Square Root of 80
Simplifying the square root of 80 involves expressing it in its simplest radical form. Here’s a detailed step-by-step process to achieve this:
- Prime Factorization:
First, factorize 80 into its prime factors:
- Grouping the Prime Factors:
Group the prime factors into pairs:
- Taking the Square Root of Each Group:
Simplify each group by taking the square root:
- Final Simplified Form:
Thus, the square root of 80 in its simplest radical form is:
This simplified form, , is often more convenient for mathematical calculations and problem-solving.

Properties of the Square Root of 80
The square root of 80 possesses several unique properties that are useful in various mathematical and practical applications. Here’s an in-depth look at these properties:
- Numeric Value:
The square root of 80 is approximately:
- Radical Form:
The simplest radical form of the square root of 80 is:
- Irrational Number:
The square root of 80 is an irrational number, meaning it cannot be expressed as a simple fraction and has a non-repeating, non-terminating decimal expansion.
- Positive and Negative Roots:
Every positive number has two square roots, one positive and one negative. Therefore:
- Product of Square Roots:
The product of the square root of 80 with itself returns the original number:
- Multiplicative Property:
The square root of a product is the product of the square roots of the factors. For 80, this can be expressed as:
- Application in Geometry:
The square root of 80 can be used to determine the length of the diagonal of a rectangle with sides of specific lengths, as well as in other geometric calculations.
Understanding the properties of the square root of 80 helps in recognizing its significance in both theoretical and practical mathematical contexts.
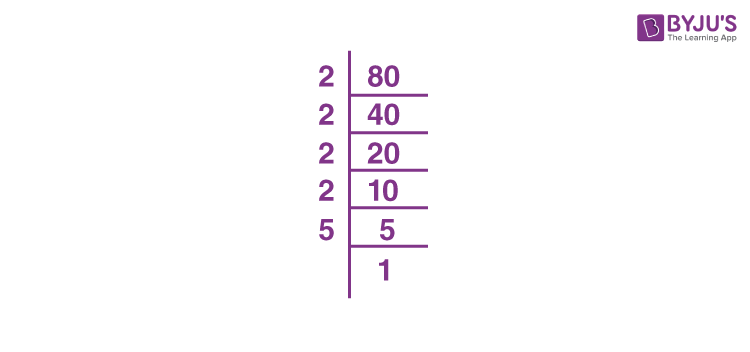
Prime Factorization and Perfect Square Factors
Understanding the prime factorization and perfect square factors of 80 helps in simplifying its square root. Here’s a detailed breakdown:
- Prime Factorization of 80:
Prime factorization is the process of expressing a number as the product of its prime factors. For 80, the prime factorization is:
- The prime factors of 80 are 2 and 5.
- There are four 2s and one 5 in the prime factorization of 80.
- Grouping the Prime Factors:
To simplify the square root, we group the prime factors into pairs:
- Each pair of 2s can be replaced by a single 2 outside the square root.
- Simplifying the Square Root:
By simplifying the square root using the grouped prime factors, we get:
- Perfect Square Factors:
A perfect square is a number that can be expressed as the square of an integer. For 80, the perfect square factor is 16 (since 16 is 4 squared):
Thus, we can further simplify the square root:
By understanding the prime factorization and identifying perfect square factors, we can simplify the square root of 80 to its simplest form, .
Positive and Negative Square Roots
When we talk about square roots, it's important to understand that every positive real number has two square roots: one positive and one negative. This is because squaring either a positive or a negative number results in a positive number.
For the number 80, its square roots can be represented as follows:
\[
\sqrt{80} \text{ and } -\sqrt{80}
\]
These two values are:
- \(\sqrt{80} \approx 8.944\)
- \(-\sqrt{80} \approx -8.944\)
The symbol \(\sqrt{}\) denotes the principal (positive) square root. Thus, when we see \(\sqrt{80}\), it refers to the positive root, approximately 8.944. The negative root is denoted as \(-\sqrt{80}\), which is approximately -8.944.
In mathematical equations and expressions, both positive and negative square roots are essential. For instance, when solving quadratic equations, we often encounter scenarios where we need to consider both roots:
\[
x^2 = 80 \implies x = \pm \sqrt{80}
\]
This indicates that the solutions to the equation are \(x = \sqrt{80}\) and \(x = -\sqrt{80}\).
Understanding both positive and negative square roots is crucial in various applications, including physics, engineering, and computer science, where we often need to calculate and consider both values in our solutions.
Applications of the Square Root of 80
The square root of 80, approximately 8.944, finds applications in various fields such as mathematics, physics, engineering, and real-world problem-solving scenarios. Here are some detailed examples:
- Geometry and Measurement: In geometry, the square root of 80 is useful in calculating dimensions and measurements. For instance, if the diagonal of a square is 80 units, the side length of the square can be found using the square root of 80.
- Engineering and Construction: Engineers and architects often encounter the square root of 80 in design calculations. For example, when determining the load-bearing capacity of materials or calculating dimensions that involve right-angled triangles, they use this square root.
- Physics: The square root of 80 appears in physics problems involving Pythagorean theorem or other equations requiring the determination of distances, speeds, or other quantities where the square of a number is involved.
- Computer Graphics: In computer graphics, calculations involving distances between points in a coordinate system often use the square root of 80 to determine the exact lengths and positions for rendering images accurately.
- Financial Modeling: In finance, the square root of 80 can be used in modeling and statistical analysis, particularly in calculating standard deviations and variances in financial data.
Here is a real-world example involving the square root of 80:
Consider a scenario where a rectangular floor needs to be painted. The floor has a length of 10 feet and a width of √80 feet. To find the area to be painted, we multiply the length by the width:
\[
\text{Area} = 10 \times \sqrt{80} \approx 10 \times 8.944 = 89.44 \text{ square feet}
\]
If the cost of painting is $5 per square foot, the total cost to paint the floor can be calculated as follows:
\[
\text{Total Cost} = 89.44 \times 5 = \$447.20
\]
This demonstrates a practical use of the square root of 80 in a cost calculation for a painting job.
Thus, the square root of 80 is not just a mathematical abstraction but a useful tool in various practical and theoretical applications.
Calculating Square Roots Using Different Methods
Calculating the square root of a number can be achieved through various methods. Below are detailed explanations of some commonly used methods to find the square root of 80.
1. Prime Factorization Method
The prime factorization method involves breaking down the number into its prime factors and pairing them to find the square root.
- Identify the prime factors of 80: \(80 = 2 \times 2 \times 2 \times 2 \times 5\)
- Pair the prime factors: \((2 \times 2) \times (2 \times 2) \times 5\)
- Select one factor from each pair and multiply them: \(2 \times 2 = 4\)
- Combine the product with the remaining factor: \(4 \times \sqrt{5} = 4\sqrt{5}\)
Thus, the simplified form of \(\sqrt{80}\) is \(4\sqrt{5}\).
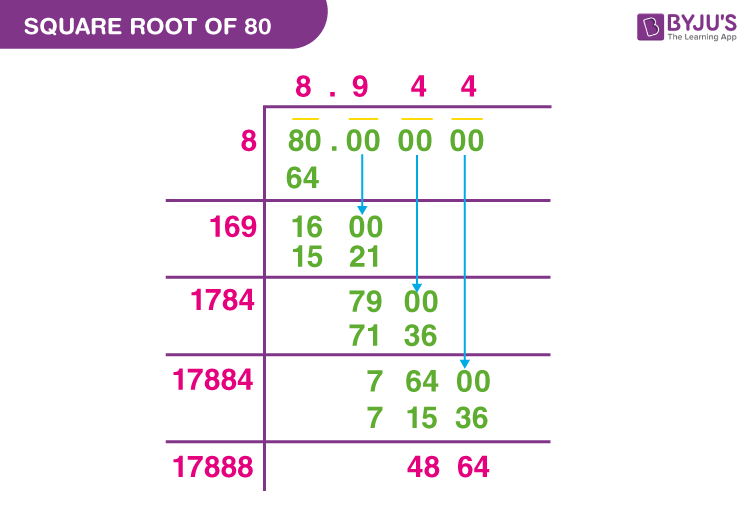
2. Long Division Method
The long division method is useful for finding square roots of large numbers. It involves a step-by-step division process similar to long division in arithmetic.
- Start by pairing the digits of 80 from right to left: \(80\)
- Find a number whose square is less than or equal to the first pair (8): \(2^2 = 4\)
- Subtract and bring down the next pair: \(80 - 4 = 4\), bring down 0 to make 40
- Double the divisor (2), making it 4. Find a number \(X\) such that \(4X \times X\) is less than or equal to 40. \(4 \times 1 = 41 \rightarrow 1\)
- The quotient (1) is part of the answer and 40-41 results in negative, so 0
- Next pair and same process till desired precision
This method provides an approximation of \(\sqrt{80}\), refined with each step.
3. Estimation Method
Estimation provides a quick way to find an approximate value of the square root. It involves finding two perfect squares between which the number lies and then interpolating.
- Identify perfect squares around 80: \(8^2 = 64\) and \(9^2 = 81\)
- Estimate closer root: \(8.9^2 \approx 79.21\), so \(\sqrt{80} \approx 8.9\)
While not as precise as other methods, it offers a quick approximation.
4. Repeated Subtraction Method
This method involves subtracting successive odd numbers from the target number until zero is reached. The count of subtractions gives the square root for perfect squares.
- Subtract successive odd numbers from 80: \(80-1, 79-3, 76-5, \ldots\) until zero is reached
- The count of subtractions will approach \(\sqrt{80}\)
This method is mainly useful for small perfect squares.
5. Using a Calculator
For a quick and accurate result, calculators with square root functions can be used.
Simply enter 80 and press the square root button to get the result: \(\sqrt{80} \approx 8.944\).
These methods offer different levels of accuracy and complexity, catering to various needs and preferences for calculating square roots.
Real-World Examples Involving the Square Root of 80
The square root of 80, approximately 8.944, has various practical applications in different fields. Here are some examples of how this value can be utilized:
-
Architecture and Construction:
Architects and construction engineers often use the square root of 80 in their calculations for designing buildings and structures. For instance, determining the length of diagonal braces or supports in a framework can involve this square root to ensure stability and proper dimensions.
-
Distance Measurement:
The Pythagorean theorem is frequently used in determining the distance between two points in a coordinate plane. If one side of a right triangle is 80 units squared, the square root helps in finding the hypotenuse, essential in fields like surveying and navigation.
-
Physics and Engineering:
In physics, the square root of 80 can be used in various formulas related to wave functions, energy calculations, and dynamics. Engineers might use it to solve problems involving areas and volumes where precise calculations are critical.
-
Statistics and Probability:
In statistics, understanding the square root of certain numbers can help in calculating standard deviations, variances, and other key statistical measures. This is important in fields that rely heavily on data analysis and interpretation.
-
Computer Graphics:
In computer graphics and game development, the square root of 80 can be used in algorithms for rendering images, calculating distances between objects, and optimizing visual effects. Efficient calculations are crucial for performance in real-time applications.
-
Financial Modeling:
Financial analysts may use square roots in models to calculate compound interest, assess risks, and perform various financial forecasts. The square root of 80 can be a part of complex formulas to determine growth rates or investment returns.
These examples illustrate how mathematical concepts like the square root of 80 are not just abstract notions but have practical implications across various professional fields.
Visualizing the Square Root of 80
Visualizing the square root of a number can help in understanding its value and applications. Here, we explore various ways to visualize the square root of 80.
1. Number Line Representation
One of the simplest ways to visualize the square root of 80 is by placing it on a number line. Given that the square root of 80 is approximately 8.944, it falls between 8 and 9 on the number line.
For more accuracy, it can be placed closer to 9, as 8.944 is almost at the mid-point between 8.9 and 9.0.
2. Geometric Representation
Square roots can also be visualized geometrically. If we draw a square with an area of 80 square units, each side of the square would be the square root of 80, which is about 8.944 units long. This can be useful in fields such as architecture and engineering where such measurements are required.

3. Graphical Representation
We can also visualize the square root of 80 using a graph of the function \(y = \sqrt{x}\). On a graph, the point where \(x = 80\) on the x-axis will correspond to \(y = \sqrt{80}\) on the y-axis.

4. Estimation and Approximation
By breaking down the number 80 into its factors, we can estimate its square root. Since 80 = 16 × 5, and we know that the square root of 16 is 4, we can estimate:
\[
\sqrt{80} = \sqrt{16 \times 5} = \sqrt{16} \times \sqrt{5} = 4 \times \sqrt{5}
\]
Knowing that \(\sqrt{5}\) is approximately 2.236, we can then calculate:
\[
4 \times 2.236 \approx 8.944
\]
5. Comparison with Nearby Square Roots
To get a better sense of where \(\sqrt{80}\) lies, compare it with nearby square roots. The square root of 81 is 9, and the square root of 64 is 8. Thus, \(\sqrt{80}\) is slightly less than 9 and more than 8. This comparison can help in quickly estimating the value without detailed calculations.
6. Visual Tools and Calculators
There are several online tools and calculators that can help visualize square roots. These tools can graph functions, create geometric shapes, and provide numerical approximations to aid in understanding and visualizing square roots like that of 80.
Using these visual methods can deepen the understanding of the concept of square roots and their practical applications.
Frequently Asked Questions
-
What is the square root of 80?
The square root of 80 is approximately 8.944, which can be expressed as \( \sqrt{80} \approx 8.944 \).
-
How can the square root of 80 be simplified?
The square root of 80 can be simplified by expressing 80 as a product of a perfect square and another number: \( \sqrt{80} = \sqrt{16 \times 5} = \sqrt{16} \times \sqrt{5} = 4\sqrt{5} \).
-
Is the square root of 80 rational or irrational?
The square root of 80 is irrational because it cannot be expressed as a fraction of two integers.
-
Can the square root of 80 be negative?
Yes, the square root of 80 has both positive and negative values: \( \pm \sqrt{80} \). The principal (positive) square root is \( \sqrt{80} \approx 8.944 \) and the negative square root is \( -\sqrt{80} \approx -8.944 \).
-
How do you calculate the square root of 80 without a calculator?
You can use the method of prime factorization or the long division method to find the square root of 80 manually. For prime factorization, express 80 as \( 80 = 2^4 \times 5 \), then simplify: \( \sqrt{80} = \sqrt{2^4 \times 5} = 4\sqrt{5} \approx 8.944 \).
-
What are some applications of the square root of 80?
The square root of 80 is used in geometry to calculate the diagonal of a square with side length 8 units, and in physics and engineering for calculations involving quadratic equations and certain formulas.
Conclusion
The exploration of the square root of 80 reveals a number that is both fascinating and practically significant. The square root of 80, approximately 8.944, has been examined through various lenses, including its mathematical properties, applications, and methods of calculation.
Understanding the square root of 80 involves recognizing it as an irrational number, which cannot be expressed as a simple fraction. The value can be simplified in radical form as \(4\sqrt{5}\), offering a clearer insight into its structure and properties.
The practical applications of the square root of 80 extend to fields such as geometry, physics, and engineering, where precise calculations are essential. Whether it is used in determining distances, solving equations, or analyzing patterns, the square root of 80 plays a crucial role.
The methods to calculate the square root of 80, ranging from manual techniques like long division to using modern calculators and computers, demonstrate the evolution of mathematical tools and the importance of accuracy in computation.
In summary, the square root of 80 is not merely a mathematical curiosity but a valuable component in various real-world contexts. Its significance underscores the beauty and utility of mathematics in solving complex problems and enhancing our understanding of the world.
Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai của 80. Video này giúp bạn hiểu rõ hơn về cách tính toán và ứng dụng căn bậc hai của 80.
Cách Đơn Giản Hóa Căn Bậc Hai của 80: sqrt(80)
READ MORE:
Hướng dẫn cách đơn giản hóa căn bậc hai của một số bằng phương pháp cây yếu tố. Video này giải thích chi tiết cách tính toán căn bậc hai của 80.
Đơn Giản Hóa Căn Bậc Hai Của Một Số Bằng Cây Yếu Tố, Sqrt(80)