Topic square root 32: The square root of 32 is an intriguing mathematical concept that combines simplicity and complexity. In this article, we will explore the value of √32, methods to calculate it, its properties, and its applications in various mathematical contexts. Join us on this enlightening journey into the world of square roots!
Table of Content
Understanding the Square Root of 32
The square root of 32 is an interesting mathematical concept that can be represented in both radical and decimal forms. Below, we will explore the value, properties, and examples involving the square root of 32.
Value of the Square Root of 32
The square root of 32, represented as , can be simplified to or approximately 5.656854.
Methods to Calculate the Square Root of 32
- Prime Factorization:
- Express 32 as the product of prime numbers: 32 = 25
- Pair the prime factors:
- Thus,
- Long Division Method: Used for more precise decimal calculation, resulting in approximately 5.656854.
Examples Using the Square Root of 32
- Simplifying Expressions:
Simplify :
- Solving Equations:
Solve :
- Real-World Application:
Finding the side length of a square window with an area of 32 square inches:
Side length = inches
Properties of the Square Root of 32
- Rational or Irrational: The square root of 32 is an irrational number, as it cannot be expressed as a simple fraction.
- Non-Terminating Decimal: The decimal form 5.656854... goes on infinitely without repeating.
Conclusion
The square root of 32, whether approached through simplification or precise calculation, offers a fascinating glimpse into the properties and applications of square roots in mathematics. Understanding its value and characteristics can be useful in both theoretical and practical contexts.

READ MORE:
Introduction
The square root of 32 is a fascinating mathematical concept often encountered in various fields. The square root of 32 is represented as √32 and can be simplified to 4√2. This simplification is essential in mathematics, especially when dealing with irrational numbers and real roots. Understanding how to find and utilize the square root of 32 is crucial for solving problems in geometry, algebra, and real-world applications.
In its decimal form, the square root of 32 is approximately 5.656. This value is significant in numerous calculations, from determining distances to solving quadratic equations. The square root of 32, being an irrational number, does not terminate or repeat, adding to its complexity and intrigue in mathematical studies.
There are various methods to calculate the square root of 32, including prime factorization and long division. These techniques help in breaking down the number into simpler components, making it easier to understand and apply in different scenarios.
This section will provide a detailed overview of the square root of 32, its properties, and its applications, ensuring a comprehensive understanding of this essential mathematical element.
Definition and Explanation
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 32 is expressed as √32. In its simplest radical form, this is equal to 4√2. When calculated as a decimal, √32 is approximately 5.656854.
To find the square root of 32, we can use methods such as prime factorization and long division.
- Prime Factorization: This method involves breaking down the number 32 into its prime factors. We get 32 = 2 × 2 × 2 × 2 × 2. By pairing the prime factors, we find that √32 = √(2×2×2×2×2) = √(16×2) = 4√2.
- Long Division: This method is useful for finding more precise decimal values. We start by pairing the digits of 32 and finding the largest number whose square is less than or equal to 32. We continue the division process to get a more accurate decimal value, which is approximately 5.656854.
The square root of 32 is an irrational number because its decimal form is non-terminating and non-repeating. Irrational numbers cannot be expressed as a simple fraction.
| Exact Form: | 4√2 |
| Decimal Form: | 5.656854 |
Calculation Methods
Calculating the square root of 32 can be done using various methods. Below are some of the common methods used to find the square root of 32:
1. Prime Factorization Method
In the prime factorization method, we break down the number into its prime factors:
- 32 can be written as \( 2 \times 2 \times 2 \times 2 \times 2 \) or \( 2^5 \).
- Group the prime factors into pairs:
- \( 32 = (2 \times 2) \times (2 \times 2) \times 2 \)
- Take one factor from each pair:
- \( \sqrt{32} = \sqrt{(2 \times 2) \times (2 \times 2) \times 2} \)
- \( \sqrt{32} = 2 \times 2 \times \sqrt{2} \)
- \( \sqrt{32} = 4\sqrt{2} \)
2. Long Division Method
The long division method involves a step-by-step division process to find the square root. Here is how it can be done for 32:
- Write 32 as 32.000000 to perform long division up to desired decimal places.
- Start by pairing the digits from the decimal point. For 32, we consider 32 as the first pair.
- Find the largest number whose square is less than or equal to 32. In this case, it is 5, because \(5^2 = 25\) and \(6^2 = 36\).
- Place 5 above the division bar and subtract 25 (which is \(5^2\)) from 32 to get a remainder of 7.
- Bring down the next pair of zeros (00) to make it 700.
- Double the quotient (5) to get 10. Find the digit X such that \(10X \times X \leq 700\). In this case, X is 6 because \(106 \times 6 = 636\).
- Place 6 in the quotient and subtract 636 from 700 to get a remainder of 64.
- Repeat the process with more pairs of zeros (bring down the next pair to make it 6400).
- Continue this method to achieve the desired precision.
| 5 | . | 6 | ... |
| 32 | 00 | ... | |
| -25 | |||
| 7 | 00 | ||
| -6 | 36 | ||
| 64 | 00 | ||
| - |
Thus, the approximate square root of 32 using the long division method is 5.656...
Prime Factorization Method
The prime factorization method is a way to simplify the calculation of the square root by breaking down the number into its prime factors. For the square root of 32, we can follow these steps:
Start by finding the prime factors of 32:
- 32 is divisible by 2, which gives 16.
- 16 is divisible by 2, which gives 8.
- 8 is divisible by 2, which gives 4.
- 4 is divisible by 2, which gives 2.
- 2 is a prime number.
So, the prime factorization of 32 is \(32 = 2 \times 2 \times 2 \times 2 \times 2\) or \(32 = 2^5\).
Group the prime factors into pairs:
- Since 32 = \(2^5\), we can write it as \(2^4 \times 2 = (2^2)^2 \times 2 = 4^2 \times 2\).
Take the square root of each pair of factors:
- \(\sqrt{32} = \sqrt{(4^2 \times 2)} = \sqrt{4^2} \times \sqrt{2}\).
Simplify the expression:
- \(\sqrt{4^2} = 4\), so \(\sqrt{32} = 4\sqrt{2}\).
Thus, the square root of 32 simplified using the prime factorization method is \(4\sqrt{2}\).
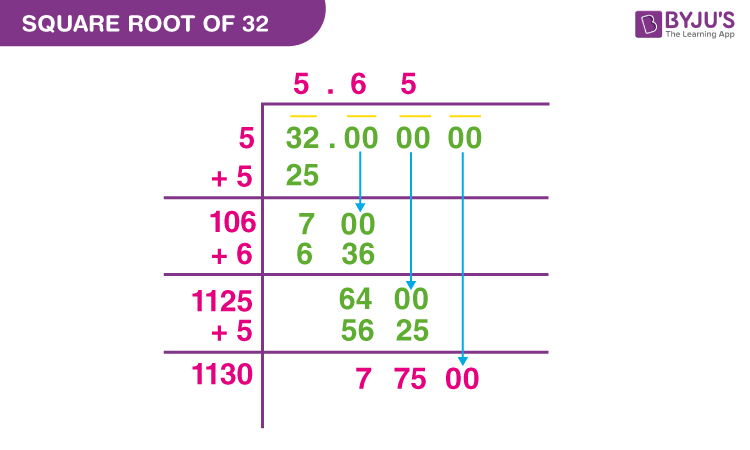
Long Division Method
The long division method is a systematic way of finding the square root of a number. Below are the steps to find the square root of 32 using this method:
- First, pair the digits of the number starting from the decimal point. For 32, we write it as 32.000000.
- Find the largest number whose square is less than or equal to the first pair. For 32, it is 5 (since 5^2 = 25 and 6^2 = 36, which is greater than 32).
- Write 5 as the first digit of the square root. Subtract 25 (5^2) from 32 to get a remainder of 7. Bring down the next pair of zeros to get 700.
- Double the number found in the quotient (5) and write it as 10 in a new row. Now we need to find a digit 'X' such that 10X * X is less than or equal to 700.
- The appropriate digit here is 7, because 107 * 7 = 749 which is too large, but 106 * 6 = 636 which is within range. So, 6 is the next digit of the quotient.
- Write 6 in the quotient, making it 5.6. Subtract 636 from 700 to get a remainder of 64. Bring down the next pair of zeros to get 6400.
- Double the current quotient (56) and write it as 112. Find the next digit 'Y' such that 112Y * Y is less than or equal to 6400.
- The appropriate digit here is 5, because 1125 * 5 = 5625 which is less than 6400. Write 5 as the next digit in the quotient.
- Write 5 in the quotient, making it 5.65. Subtract 5625 from 6400 to get a remainder of 775. Bring down the next pair of zeros to get 77500.
- Repeat the steps until you reach the desired level of accuracy. For example, the next step would involve doubling 565 to get 1130 and finding the next digit 'Z' to satisfy 1130Z * Z ≤ 77500.
Continuing this process, you can find more digits of the square root of 32. Using the long division method, we can approximate the square root of 32 as:
\(\sqrt{32} \approx 5.656\)
This method provides a systematic approach to finding the square root of any number, giving us a precise decimal representation step by step.
Decimal Representation
The square root of 32 is an irrational number, which means its decimal representation is non-terminating and non-repeating. The approximate value of the square root of 32 in decimal form is:
\(\sqrt{32} \approx 5.6568542495\)
To understand this better, let's break down the decimal representation into a more detailed form. Here are the steps:
- Step 1: Estimate the square root to the nearest whole number. For 32, this is between 5 and 6.
- Step 2: Refine the estimate to find a more precise value. We know that:
- \(5^2 = 25\)
- \(6^2 = 36\)
- Step 3: Use a more precise method, like long division or a calculator, to find the exact decimal representation up to the desired number of decimal places.
The long division method or using a calculator will yield the value:
\(\sqrt{32} \approx 5.6568542495\)
This value shows that the decimal representation of the square root of 32 is non-terminating and does not repeat, making it an irrational number.
Irrational Number
The square root of 32 is classified as an irrational number. This classification arises from its decimal representation and its inability to be expressed as a fraction of two integers.
Here are the key points that highlight why the square root of 32 is an irrational number:
- Non-repeating, Non-terminating Decimal: The decimal representation of the square root of 32 is approximately 5.656854. This decimal goes on forever without repeating, which is a hallmark of irrational numbers.
- Fraction Form: An irrational number cannot be precisely expressed as a ratio of two integers. For √32, there are no integers p and q such that √32 = p/q.
- Prime Factorization: When breaking down 32 into its prime factors, we get 2 × 2 × 2 × 2 × 2, or \(2^5\). In its simplest radical form, √32 can be expressed as \(4\sqrt{2}\), where √2 is known to be irrational. Since the product of a rational number (4) and an irrational number (√2) is irrational, √32 is also irrational.
The irrational nature of the square root of 32 has significant implications in mathematics, particularly in fields dealing with algebra and number theory. Understanding the properties of irrational numbers helps in solving complex equations and in the analysis of numerical patterns.
Thus, the square root of 32, with its endless, non-repetitive decimal expansion, firmly places it in the category of irrational numbers.
Applications and Examples
The square root of 32, approximately 5.656, has numerous applications and can be illustrated through various examples. Understanding these applications can enhance comprehension and demonstrate the relevance of mathematical concepts in real-world scenarios.
Applications
- Geometry and Trigonometry: The square root of 32 often appears in geometric calculations involving right triangles, where it can represent the length of the hypotenuse or other sides.
- Physics: In physics, square roots are used to solve problems involving areas, velocities, and other measurements. The square root of 32 could be used to determine quantities such as root mean square velocities in gas dynamics.
- Engineering: Engineers use square roots in various calculations, including those related to stress, strain, and electrical circuits. The square root of 32 might be relevant in determining tolerances or material properties.
- Statistics: Square roots are crucial in statistical formulas, such as standard deviations and variance calculations, which can involve the square root of 32 when dealing with specific data sets.
Examples
-
Example 1: Simplifying Expressions
Given the expression \( \sqrt{32} + 3\sqrt{8} \), simplify it.
Solution:
- First, express both square roots in their simplest radical forms: \( \sqrt{32} = 4\sqrt{2} \) and \( \sqrt{8} = 2\sqrt{2} \).
- Then, substitute these values into the expression: \( 4\sqrt{2} + 3 \times 2\sqrt{2} \).
- Combine like terms: \( 4\sqrt{2} + 6\sqrt{2} = 10\sqrt{2} \).
- Therefore, the simplified form is \( 10\sqrt{2} \).
-
Example 2: Solving Real-life Problems
Joseph wants to cover her bathroom floor with tiles. The floor is square-shaped and has an area of 32 square feet. What is the length of one side of the floor?
Solution:
- Let the side length of the floor be \( x \) feet.
- Since the area is \( 32 \) square feet, we have \( x^2 = 32 \).
- Taking the square root of both sides, \( x = \sqrt{32} \approx 5.656 \) feet.
- Therefore, the length of one side of the floor is approximately 5.656 feet.
These examples highlight how the square root of 32 is used in mathematical simplification and practical problem-solving. By mastering such concepts, one can apply mathematical principles effectively in various disciplines.

Simplification of Expressions
The process of simplifying the square root of 32 involves breaking down the number into its prime factors and then using the properties of square roots to simplify the expression. Here's a detailed step-by-step explanation:
- Prime Factorization:
First, we perform prime factorization of 32:
\(32 = 2 \times 2 \times 2 \times 2 \times 2 = 2^5\)
- Group the Prime Factors:
Next, we group the prime factors into pairs:
\(32 = (2 \times 2) \times (2 \times 2) \times 2 = 2^2 \times 2^2 \times 2\)
- Simplify the Square Root:
Using the property of square roots, \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\), we can simplify the square root of 32:
\(\sqrt{32} = \sqrt{2^2 \times 2^2 \times 2} = \sqrt{(2^2)} \times \sqrt{(2^2)} \times \sqrt{2}\)
\(\sqrt{32} = 2 \times 2 \times \sqrt{2} = 4\sqrt{2}\)
Therefore, the simplified form of the square root of 32 is \(4\sqrt{2}\).
Example:
Let's take an example to see how the simplification of \(\sqrt{32}\) can be applied:
- Original Expression:
Suppose we have the expression \(3\sqrt{32}\).
- Simplification Step:
We can replace \(\sqrt{32}\) with its simplified form:
\(3\sqrt{32} = 3 \times 4\sqrt{2}\)
- Final Result:
Multiply the constants together:
\(3 \times 4\sqrt{2} = 12\sqrt{2}\)
Hence, the expression \(3\sqrt{32}\) simplifies to \(12\sqrt{2}\).
Real-life Examples and Problems
The concept of the square root, including the square root of 32, finds numerous applications in various real-life scenarios. Understanding these applications helps in appreciating the importance of square roots in different fields.
-
Architecture and Construction
In architecture, square roots are essential in calculating dimensions and ensuring the structural integrity of buildings. For instance, the length of diagonal supports or braces in a structure can be determined using the Pythagorean theorem, which involves square roots.
Example: To find the diagonal support in a rectangular frame measuring 6 feet by 8 feet, you use the formula:
\(\sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10\) feet.
-
Finance
Square roots are used in finance to calculate volatility, which is a measure of how much a stock’s price varies over time. Volatility is derived by taking the square root of the variance.
-
Navigation
In navigation, square roots help in computing distances between points on a map using the distance formula, which is derived from the Pythagorean theorem.
Example: To find the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\):
\(D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\).
For points (1, 3) and (8, -5):
\(D = \sqrt{(8-1)^2 + (-5-3)^2} = \sqrt{7^2 + (-8)^2} = \sqrt{49 + 64} = \sqrt{113}\).
-
Science and Engineering
Square roots are prevalent in science for various calculations, such as determining the speed of an object, the intensity of sound waves, or the amount of radiation absorbed.
In electrical engineering, square roots are used to calculate power, voltage, and current in circuits, which are crucial for designing and analyzing electrical systems.
-
Computer Graphics
In computer graphics, square roots are used in various calculations, such as finding the distance between points in 2D or 3D space, which is crucial for rendering images and animations accurately.
These examples illustrate how the mathematical concept of square roots, such as the square root of 32, is integral to practical applications across different fields, from construction to finance and science.
Cách Đơn Giản Hóa Căn Bậc Hai Của 32: Sqrt(32)
READ MORE:
Cách Đơn Giản Hóa Căn Bậc Hai Của 32







