Topic square root algorithm: Discover the fascinating world of square root algorithms, exploring efficient methods for calculating square roots, their mathematical foundations, and practical applications. Learn about classical techniques like the Babylonian method, Newton's iteration, and modern computational approaches. Enhance your understanding of how these algorithms solve real-world problems and their significance in various fields.
Table of Content
- Square Root Algorithm
- Introduction to Square Root Algorithms
- Newton's Method (Heron's Method)
- Binary Search Method
- Fast Inverse Square Root Algorithm
- Approximation Methods
- Implementation Examples in Programming Languages
- Applications of Square Root Algorithms
- Common Challenges and Solutions
- Comparative Analysis of Different Methods
- Conclusion and Future Directions
- YOUTUBE: Đây là video giới thiệu về thuật toán căn bậc hai, cách hoạt động và ý nghĩa của nó bởi Nathan Dalaklis.
Square Root Algorithm
The square root algorithm is a method to determine the square root of a number. Various algorithms have been developed over time, each with its own advantages and use cases. Below, we explore some of the most prominent square root algorithms.
Digit-by-Digit Algorithm
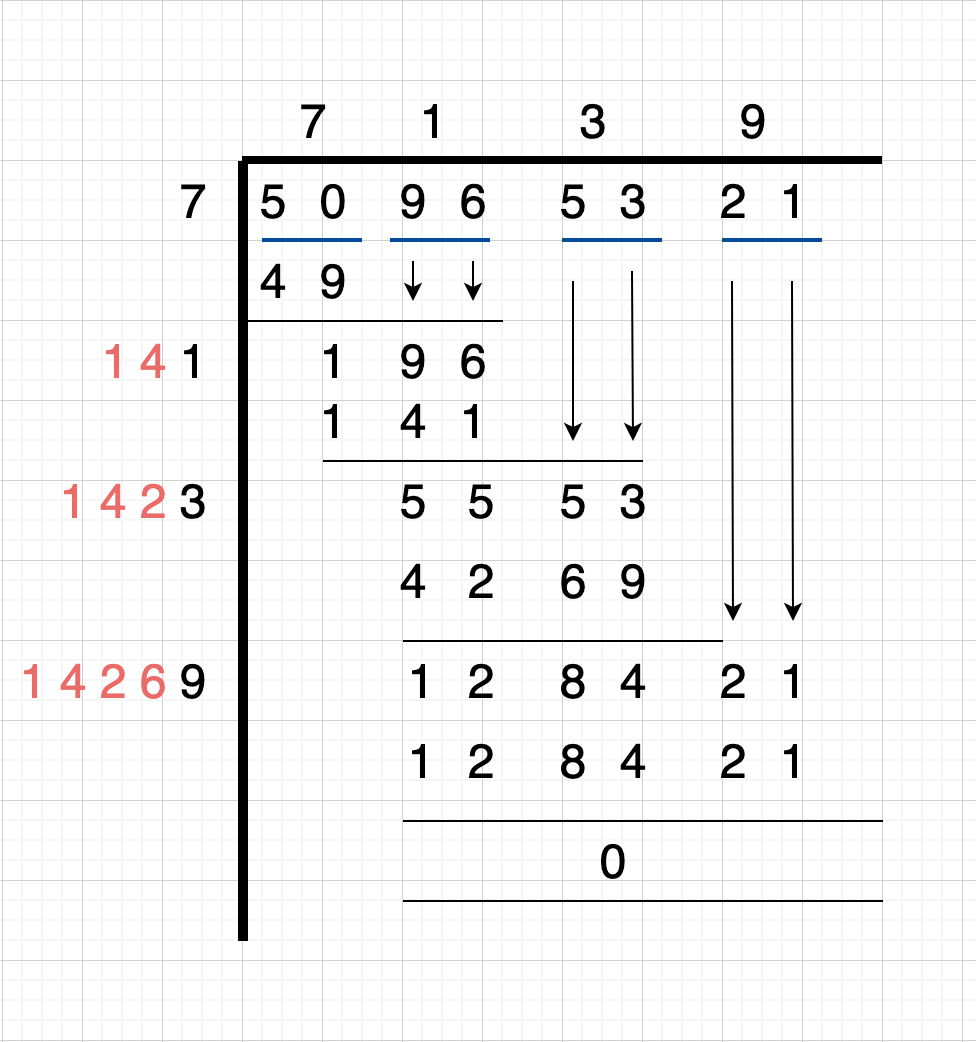
This traditional method, often taught in schools, involves finding the square root digit by digit. The basic principle can be illustrated with an example of finding the square root of a number Z, which is the square of a two-digit number XY:
\[ Z = (10X + Y)^2 = 100X^2 + 20XY + Y^2 \]
The algorithm proceeds by determining the largest digit X such that \( X^2 \leq Z \). In subsequent steps, each new digit of the root is determined by refining the estimate using multiplication and subtraction.
Babylonian Method
Also known as Heron's method, this iterative algorithm starts with an initial guess and refines it repeatedly:
\[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right) \]
This method converges quickly and is widely used due to its simplicity and effectiveness.
Fast Inverse Square Root
This algorithm, famous for its use in computer graphics, particularly in the game Quake III Arena, provides a fast approximation of the inverse square root. The core idea involves bit manipulation to achieve a rapid initial approximation followed by one iteration of Newton's method for refinement:
\[ y = y \left( \text{threehalfs} - ( x2 \cdot y \cdot y ) \right) \]
This method is celebrated for its speed and efficiency, despite being less accurate than other methods.
Integer Square Root
For integer inputs, an efficient algorithm computes the integer square root using bit manipulation and iterative refinement. The basic idea can be implemented in C as follows:
unsigned int int_sqrt(unsigned int s) {
if (s <= 1) return s;
unsigned int x0 = s / 2;
unsigned int x1 = (x0 + s / x0) / 2;
while (x1 < x0) {
x0 = x1;
x1 = (x0 + s / x0) / 2;
}
return x0;
}
Worked Examples
- Digit-by-Digit Example: To find the square root of 2685, double the current estimate, find the largest possible next digit, and iterate until the desired precision is achieved.
- Babylonian Example: Starting with an initial guess of 1 for the square root of 30, successive iterations yield improved approximations.
- Fast Inverse Square Root Example: Using the bit manipulation trick on 0.15625 results in a rapid approximation followed by one iteration of refinement.
Conclusion
Each algorithm has its own niche, with some being more suitable for manual calculations, others optimized for computational efficiency, and some tailored for specific numerical types. Understanding these algorithms provides a robust toolkit for various mathematical and computational applications.
READ MORE:
Introduction to Square Root Algorithms
Square root algorithms are methods used to find the principal square root of a number. These algorithms range from ancient manual methods to modern computational techniques. Understanding these algorithms is crucial for various applications in mathematics, computer science, and engineering.
Several popular algorithms for computing square roots include:
- Babylonian Method (Heron's Method)
- Digit-by-Digit Calculation
- Newton's Iteration (Newton-Raphson Method)
- Continued Fractions
The Babylonian Method is an iterative algorithm that starts with an initial guess and refines it repeatedly using the formula:
\[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right) \]
where \( S \) is the number whose square root is being computed, and \( x_n \) is the current approximation.
The Digit-by-Digit Calculation method involves finding each digit of the square root sequentially. It is a manual method suitable for hand calculations, though less efficient for software implementations.
Newton's Iteration is a powerful method that converges quadratically to the square root. The iteration formula is:
\[ x_{k+1} = \frac{1}{2} \left( x_k + \frac{S}{x_k} \right) \]
This method is widely used due to its fast convergence rate.
Continued Fractions provide another way to compute square roots by expressing them as a sequence of fractions. This method, known for its precision, can be more complex to implement but offers high accuracy.
Each of these methods has its advantages and disadvantages, making them suitable for different contexts and computational environments.
Newton's Method (Heron's Method)
Newton's Method, also known as Heron's Method, is an efficient iterative technique for finding the square root of a positive number \( S \). The method starts with an initial guess \( x_0 \) and refines this guess through successive iterations to approximate the square root.
The iterative formula used in Newton's Method is:
\[
x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right)
\]
Here is a step-by-step explanation of the method:
-
Initialization: Start with an initial guess \( x_0 \). A common choice is \( x_0 = \frac{S}{2} \) or any other positive value. -
Iteration: Use the iterative formula to compute the next approximation:
\[
x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right)
\]
Continue this process until the difference between successive approximations is smaller than a predefined tolerance level \( \epsilon \). -
Convergence: The method converges quadratically, meaning that the number of correct digits roughly doubles with each iteration, making it a very efficient algorithm for finding square roots.
For example, to find the square root of 25:
Let's start with \( x_0 = 5 \):
| Iteration | Value |
| 0 | \( x_0 = 5 \) |
| 1 | \( x_1 = \frac{1}{2} \left( 5 + \frac{25}{5} \right) = 5 \) |
Since the initial guess was already the square root, the method converges immediately. For other values of \( S \), the iterations would proceed similarly until convergence.
Newton's Method is widely used in numerical computations due to its simplicity and rapid convergence, making it a fundamental tool in scientific and engineering applications.
Binary Search Method
The Binary Search Method for calculating square roots is an iterative approach that leverages the properties of binary search to efficiently converge on the square root of a given number.
Here's a step-by-step outline of the Binary Search Method:
- Choose an initial range for the square root approximation, typically between 0 and the number whose square root is being calculated.
- Calculate the midpoint of the current range.
- Compare the square of the midpoint with the target number:
- If the square of the midpoint equals the target number, the midpoint is the square root.
- If the square of the midpoint is less than the target number, adjust the range to search the upper half.
- If the square of the midpoint is greater than the target number, adjust the range to search the lower half.
- Repeat steps 2-4 until the desired precision is achieved or until convergence criteria are met.
The Binary Search Method is particularly useful for its efficiency in narrowing down the square root with each iteration, making it suitable for applications where precision and speed are paramount.
Fast Inverse Square Root Algorithm
The Fast Inverse Square Root Algorithm is a famous method for approximating the reciprocal of a square root with high speed.
Here's a step-by-step outline of the Fast Inverse Square Root Algorithm:
- Start with an initial floating-point approximation of the input number's inverse square root.
- Perform an initial approximation using bit manipulation and a magic number.
- Refine the approximation using Newton's method to improve accuracy.
- Iterate through the refinement process until the desired precision is achieved.
The algorithm gained popularity due to its efficient implementation in early 3D graphics engines, notably in the Quake III Arena game engine.

Approximation Methods
Approximation Methods for calculating square roots encompass various techniques designed to provide quick and reasonably accurate estimations.
Here are some common approximation methods:
- Linear Approximation: Uses a linear function to approximate the square root, often based on the tangent line approximation near a point.
- Newton's Method: Iteratively improves an initial guess by using the tangent line of the function at each iteration.
- Binomial Series: Expands the square root function into a series approximation, often used for small values or in contexts where rapid calculations are necessary.
- Continued Fractions: Represents the square root as a continued fraction, allowing for successive refinements to achieve better approximations.
Each method has its strengths and applicability, catering to different computational needs and requirements for precision.
Implementation Examples in Programming Languages
Implementing square root algorithms in various programming languages allows for practical application and integration into software systems.
Here are examples of implementing square root algorithms in different programming languages:
- Python:
- Using the built-in
math.sqrt()function for straightforward square root calculation. - Implementing the Babylonian Method using iterative approximation.
- Using the built-in
- C:
- Using standard library functions like
sqrt()frommath.h. - Writing custom functions to implement Newton's Method or other algorithms for square root calculation.
- Using standard library functions like
- Java:
- Utilizing
java.lang.Mathmethods such asMath.sqrt()for precise square root computation. - Implementing iterative methods or mathematical algorithms directly in Java code.
- Utilizing
- JavaScript:
- Using the
Math.sqrt()function for simple square root calculation in client-side scripts. - Implementing algorithms like the Babylonian Method in JavaScript for more customized applications.
- Using the
Each programming language offers unique libraries and capabilities for implementing square root algorithms, catering to specific requirements and performance considerations.
Applications of Square Root Algorithms
Square root algorithms find application in various fields where precise computation of square roots is necessary. Here are some common applications:
- Engineering: In engineering disciplines such as structural analysis and signal processing, square root calculations are essential for determining parameters like resonance frequencies and material stress.
- Computer Graphics: Algorithms like Newton's method are used extensively in computer graphics to compute lighting effects and geometric transformations.
- Financial Modeling: Financial analysts use square root algorithms for risk assessment models, volatility calculations, and option pricing formulas.
- Scientific Computing: In scientific research, these algorithms play a crucial role in simulations, data analysis, and modeling natural phenomena.
- Navigation Systems: GPS navigation systems employ square root algorithms to calculate distances and positions accurately.
- Machine Learning: Optimization algorithms that involve gradient descent often require square root computations, particularly in regularization techniques.
These applications highlight the versatility and importance of square root algorithms across various domains, showcasing their fundamental role in modern computational techniques.
Common Challenges and Solutions
While square root algorithms are powerful tools, they also present several challenges that developers often encounter. Here are some common issues and their solutions:
- Numerical Stability: Algorithms like Newton's method can be sensitive to initial guesses, leading to divergence or slow convergence. Solutions involve choosing appropriate initial values and implementing robust error handling.
- Complexity: Certain algorithms, such as binary search methods for integer square roots, require careful implementation to handle edge cases like overflow and underflow. Ensuring efficient boundary checks and data type handling can mitigate these issues.
- Precision: Achieving desired precision in square root calculations can be challenging due to floating-point arithmetic limitations. Techniques like iterative refinement and adaptive precision adjustments help improve accuracy.
- Performance: Some algorithms may exhibit varying performance characteristics depending on input data distributions. Optimizing algorithmic parameters and leveraging parallel computing techniques can enhance computational efficiency.
- Implementation Errors: Errors in algorithm implementation can lead to incorrect results or runtime exceptions. Thorough testing, peer review, and using established libraries or frameworks can reduce implementation risks.
Addressing these challenges ensures that square root algorithms perform reliably across different applications, contributing to their effective use in computational tasks.

Comparative Analysis of Different Methods
There are several algorithms for computing the square root, each with its strengths and weaknesses. Here's a comparative analysis:
- Digit-by-Digit Algorithm: This method calculates square roots digit by digit, making it suitable for environments with limited computational resources. However, it can be slower for larger numbers due to its iterative nature.
- Newton's Method (Heron's Method): Known for its rapid convergence, Newton's method is efficient but requires initial guesswork and may suffer from instability when used with certain functions.
- Binary Search Method: Effective for finding square roots in sorted arrays, this method divides the search space by half in each step. It's optimal for scenarios where precision is critical and the input is ordered.
- Fast Inverse Square Root Algorithm: Originally developed for fast computation in 3D game engines, it utilizes bitwise operations and is highly optimized for speed. However, it sacrifices precision for performance.
- Integer Square Root: This method finds the largest integer whose square is less than or equal to the given number. It's straightforward but lacks the precision of methods that compute exact decimal approximations.
- Babylonian Method: A classic iterative algorithm that repeatedly averages an initial guess with the number divided by the guess. It converges quickly but may require many iterations for high precision.
- Approximation Methods: Techniques like Taylor series expansions or continued fractions offer varying levels of precision and speed, depending on the complexity of the approximation used.
Choosing the right algorithm depends on the specific requirements of the application, including speed, accuracy, and available computational resources. For instance, real-time applications may favor faster but less precise algorithms, while scientific computing may prioritize accuracy.
Conclusion and Future Directions
In conclusion, square root algorithms play a crucial role in various fields ranging from mathematics to computer science and engineering. Each algorithm discussed offers unique advantages depending on the specific requirements of precision, computational resources, and speed.
Looking ahead, future developments in square root algorithms are likely to focus on:
- Enhancing computational efficiency: Developing algorithms that strike a balance between speed and accuracy, particularly for large-scale computations.
- Improving numerical stability: Addressing issues of stability and convergence especially in iterative methods like Newton's and Babylonian methods.
- Integrating with emerging technologies: Adapting algorithms to leverage advancements in parallel computing, quantum computing, and machine learning for faster and more precise calculations.
- Exploring novel approaches: Investigating alternative mathematical frameworks and algorithms to achieve superior performance in specific applications.
Overall, the evolution of square root algorithms continues to be driven by the pursuit of faster, more accurate computations to meet the demands of modern computing and scientific research.
Đây là video giới thiệu về thuật toán căn bậc hai, cách hoạt động và ý nghĩa của nó bởi Nathan Dalaklis.
WHAT IS THE SQUARE ROOT ALGORITHM? How does the square root algorithm work and why | Nathan Dalaklis
READ MORE:
Video giải thích thuật toán nghịch đảo căn bậc hai nhanh được sử dụng trong game Quake III.
Fast Inverse Square Root — Thuật toán trong Quake III