Topic simplify square roots with fractions: Unlock the secrets to simplifying square roots with fractions in our comprehensive guide. Whether you're a student or a math enthusiast, this article provides clear, step-by-step instructions to help you master this essential math skill. Learn the methods, avoid common mistakes, and practice with examples to build your confidence and proficiency.
Table of Content
- Simplifying Square Roots with Fractions
- Introduction to Square Roots and Fractions
- Basic Concepts of Square Roots
- Understanding Fractions
- Properties of Square Roots
- Methods for Simplifying Square Roots
- Prime Factorization Method
- Simplifying Fractions under Square Roots
- Step-by-Step Guide to Simplification
- Separating Numerator and Denominator
- Simplifying the Numerator
- Simplifying the Denominator
- Combining Simplified Results
- Rationalizing the Denominator
- Common Mistakes to Avoid
- Practice Problems and Solutions
- Advanced Techniques
- Applications of Simplified Square Roots
- Conclusion
- YOUTUBE: Video này hướng dẫn cách đơn giản hóa phân số dưới dấu căn với các thủ thuật toán học để giúp bạn giải quyết các vấn đề phức tạp một cách dễ dàng.
Simplifying Square Roots with Fractions
When simplifying square roots that contain fractions, we can use a combination of the prime factorization method and properties of radicals. Here’s a detailed, step-by-step guide:
Step-by-Step Simplification Process
-
Identify the Fraction: Start by recognizing the fraction under the square root. For example, consider \( \sqrt{\frac{a}{b}} \).
-
Separate the Numerator and Denominator: Use the property of square roots to separate the numerator and the denominator.
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\] -
Simplify the Square Roots: Simplify each square root individually.
-
For the numerator \( \sqrt{a} \): Find the prime factors of \( a \) and simplify.
Example: \( \sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2} \)
-
For the denominator \( \sqrt{b} \): Find the prime factors of \( b \) and simplify.
Example: \( \sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2} \)
-
-
Combine the Results: After simplifying both the numerator and the denominator, combine the results back into a single fraction.
\[
\frac{\sqrt{a}}{\sqrt{b}} = \frac{\text{Simplified Numerator}}{\text{Simplified Denominator}}
\] -
Rationalize the Denominator: If the denominator contains a square root, rationalize it by multiplying both the numerator and the denominator by a value that will eliminate the square root in the denominator.
Example: For \( \frac{3\sqrt{2}}{5\sqrt{2}} \), multiply by \( \frac{\sqrt{2}}{\sqrt{2}} \).
\[
\frac{3\sqrt{2}}{5\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{3 \cdot 2}{5 \cdot 2} = \frac{6}{10} = \frac{3}{5}
\]
Examples
-
Simplify \( \sqrt{\frac{8}{2}} \)
\[
\sqrt{\frac{8}{2}} = \frac{\sqrt{8}}{\sqrt{2}} = \frac{\sqrt{2 \times 2^2}}{\sqrt{2}} = \frac{2\sqrt{2}}{\sqrt{2}} = 2
\] -
Simplify \( \sqrt{\frac{18}{50}} \)
\[
\sqrt{\frac{18}{50}} = \frac{\sqrt{18}}{\sqrt{50}} = \frac{3\sqrt{2}}{5\sqrt{2}} = \frac{3}{5}
\]
Practice Problems
Try simplifying the following square roots with fractions:
- Simplify \( \sqrt{\frac{27}{3}} \)
- Simplify \( \sqrt{\frac{32}{8}} \)
- Simplify \( \sqrt{\frac{45}{5}} \)

READ MORE:
Introduction to Square Roots and Fractions
Square roots and fractions are fundamental concepts in mathematics that often appear together in various problems. Understanding how to simplify square roots that contain fractions is crucial for solving complex mathematical expressions and equations. This section will provide a detailed explanation of these concepts and methods to simplify them effectively.
A square root represents a value that, when multiplied by itself, gives the original number. For instance, the square root of 9 is 3, as \(3 \times 3 = 9\). When square roots involve fractions, the process of simplification can be more complex but follows systematic steps.
Fractions consist of two parts: a numerator and a denominator. Simplifying square roots with fractions can involve different scenarios such as:
- Simplifying the square root of a simple fraction
- Simplifying fractions within square roots
- Rationalizing the denominator when it contains a square root
Let's delve into these methods:
Simplifying the Square Root of a Simple Fraction
When simplifying the square root of a fraction, such as \(\sqrt{\frac{a}{b}}\), you can use the property that the square root of a fraction is the fraction of the square roots:
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]
For example:
\[
\sqrt{\frac{16}{25}} = \frac{\sqrt{16}}{\sqrt{25}} = \frac{4}{5}
\]
Simplifying Fractions Within Square Roots
Sometimes, you may encounter a fraction inside a square root that can be simplified first to make the calculation easier. Consider the example:
\[
\sqrt{\frac{18}{50}}
\]
First, simplify the fraction inside the square root:
\[
\frac{18}{50} = \frac{9}{25}
\]
Then, apply the square root to the simplified fraction:
\[
\sqrt{\frac{9}{25}} = \frac{\sqrt{9}}{\sqrt{25}} = \frac{3}{5}
\]
Rationalizing the Denominator
If you have a square root in the denominator of a fraction, such as \(\frac{a}{\sqrt{b}}\), you need to rationalize the denominator by eliminating the square root. Multiply both the numerator and the denominator by the square root of the denominator:
\[
\frac{a}{\sqrt{b}} \times \frac{\sqrt{b}}{\sqrt{b}} = \frac{a \cdot \sqrt{b}}{b}
\]
For example:
\[
\frac{5}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{5\sqrt{2}}{2}
\]
These methods allow for the simplification of square roots involving fractions, making complex expressions easier to handle and solve.
Basic Concepts of Square Roots
Square roots are fundamental concepts in mathematics, often represented as \( \sqrt{} \). The square root of a number \( a \) is a value \( b \) such that \( b^2 = a \). Understanding square roots is essential for simplifying expressions, especially when dealing with fractions.
Here are some basic steps to simplify square roots:
- Identify Perfect Squares: Check if the number under the square root is a perfect square (e.g., 4, 9, 16). For example, \( \sqrt{9} = 3 \).
- Factorization: If the number is not a perfect square, factor it into smaller numbers. For instance, \( \sqrt{18} \) can be factored as \( \sqrt{9 \times 2} \), which simplifies to \( 3\sqrt{2} \).
- Prime Factorization: Break the number down into its prime factors. For example, \( \sqrt{72} \) can be factored as \( \sqrt{36 \times 2} = 6\sqrt{2} \).
When dealing with fractions involving square roots, the process includes:
- Simplify the Square Root: Simplify any square roots in the fraction's numerator or denominator.
- Rationalize the Denominator: If the denominator contains a square root, multiply both the numerator and the denominator by the conjugate of the denominator to remove the square root.
Let's see an example:
To simplify \( \frac{5}{\sqrt{3}} \):
- Simplify the Square Root: \( \sqrt{3} \) is already simplified.
- Rationalize the Denominator: Multiply both the numerator and denominator by \( \sqrt{3} \).
- \[ \frac{5}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{5\sqrt{3}}{3} \]
Therefore, \( \frac{5}{\sqrt{3}} \) simplifies to \( \frac{5\sqrt{3}}{3} \).
By following these steps, you can simplify square roots and fractions efficiently, making complex calculations more manageable.
Understanding Fractions
Fractions are a way to represent parts of a whole. They consist of a numerator, which is the number above the fraction bar, and a denominator, which is the number below the fraction bar. Fractions can be categorized as proper, improper, or mixed numbers. Here are the key points to understand about fractions:
- Proper Fractions: These fractions have a numerator smaller than the denominator, such as \( \frac{3}{4} \).
- Improper Fractions: These fractions have a numerator larger than or equal to the denominator, such as \( \frac{7}{4} \).
- Mixed Numbers: These consist of a whole number and a proper fraction combined, such as \( 1\frac{3}{4} \).
When working with fractions, it's often necessary to simplify them or convert them to a different form to make calculations easier. Here are some basic steps and rules for working with fractions:
- Simplifying Fractions: To simplify a fraction, divide the numerator and the denominator by their greatest common divisor (GCD). For example, \( \frac{8}{12} \) can be simplified by dividing both 8 and 12 by their GCD, which is 4, resulting in \( \frac{2}{3} \).
- Converting Improper Fractions to Mixed Numbers: Divide the numerator by the denominator to get the whole number part, and use the remainder as the new numerator. For example, \( \frac{9}{4} \) can be converted to \( 2\frac{1}{4} \).
- Adding and Subtracting Fractions: To add or subtract fractions, make sure they have a common denominator. Adjust the fractions as needed, then add or subtract the numerators and keep the common denominator. For example, \( \frac{1}{4} + \frac{3}{4} = \frac{4}{4} = 1 \).
- Multiplying Fractions: Multiply the numerators together and the denominators together. Simplify the result if possible. For example, \( \frac{2}{3} \times \frac{3}{4} = \frac{6}{12} = \frac{1}{2} \).
- Dividing Fractions: Multiply by the reciprocal of the divisor. For example, \( \frac{2}{3} \div \frac{4}{5} \) is equivalent to \( \frac{2}{3} \times \frac{5}{4} = \frac{10}{12} = \frac{5}{6} \).
Understanding these fundamental concepts and operations with fractions is crucial for simplifying more complex expressions, such as those involving square roots within fractions.
Properties of Square Roots
Understanding the properties of square roots is essential for simplifying expressions and solving equations. Below are some fundamental properties of square roots that will aid in your mathematical journey:
- Product Property: The square root of a product is equal to the product of the square roots. Mathematically, this is expressed as \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \) for any non-negative numbers \(a\) and \(b\).
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots. This property is written as \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) where \(a \geq 0\) and \(b > 0\).
- Square of a Square Root: The square of a square root returns the original value, i.e., \( (\sqrt{a})^2 = a \). This is true for any non-negative number \(a\).
- Non-negative Property: Square roots always yield non-negative results, \( \sqrt{a} \geq 0 \) for \( a \geq 0 \).
These properties allow for the simplification of complex expressions involving square roots and make it easier to solve equations that include them. Let's apply these properties with some examples:
- Using the product property: \( \sqrt{45} = \sqrt{9 \cdot 5} = \sqrt{9} \cdot \sqrt{5} = 3\sqrt{5} \)
- Applying the quotient property: \( \sqrt{\frac{25}{16}} = \frac{\sqrt{25}}{\sqrt{16}} = \frac{5}{4} \)
- Squaring a square root: \( (\sqrt{7})^2 = 7 \)
By mastering these properties, you can simplify square roots effectively and handle fractions that include square roots with confidence.

Methods for Simplifying Square Roots
There are several methods to simplify square roots. Here, we will discuss the most common techniques that can be applied to various types of square root problems.
Prime Factorization Method
This method involves breaking down the number under the square root into its prime factors.
- Find the prime factors of the number inside the square root.
- Group the prime factors into pairs.
- Move one number from each pair outside the square root.
For example:
\(\sqrt{72}\)
Prime factorize 72: \(72 = 2 \times 2 \times 2 \times 3 \times 3\)
Group the prime factors: \( (2 \times 2) \times (2) \times (3 \times 3)\)
Move one number from each pair outside: \(2 \times 3 \sqrt{2} = 6\sqrt{2}\)
Simplifying Fractions
When dealing with fractions, the process involves simplifying the numerator and the denominator separately.
- Simplify the numerator and the denominator separately.
- Apply the square root to both the numerator and the denominator.
- If possible, reduce the resulting fraction.
For example:
\(\sqrt{\frac{18}{50}}\)
Simplify inside the square root: \(\sqrt{\frac{9}{25}}\)
Apply the square root to the numerator and the denominator: \(\frac{\sqrt{9}}{\sqrt{25}} = \frac{3}{5}\)
Using the Quotient Rule
The quotient rule states that the square root of a fraction is the fraction of the square roots.
For example:
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
Apply this rule to simplify square roots in fractions easily.
Rationalizing the Denominator
Rationalizing the denominator involves removing the square root from the denominator.
- Multiply the numerator and the denominator by a number that will remove the square root in the denominator.
For example:
\(\frac{1}{\sqrt{2}}\)
Multiply by \(\frac{\sqrt{2}}{\sqrt{2}}\): \(\frac{1 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} = \frac{\sqrt{2}}{2}\)
Prime Factorization Method
The prime factorization method is a systematic way to simplify square roots. This method involves breaking down the number under the square root into its prime factors and then simplifying by grouping pairs of identical factors.
- First, factorize the number under the square root into its prime factors. For example, let's consider the number 72:
- \(72 = 2 \times 2 \times 2 \times 3 \times 3\)
- Next, pair the prime factors. Each pair of identical factors can be taken out of the square root as a single factor:
- \(72 = (2 \times 2) \times (2 \times 3 \times 3)\)
- Simplify the square root by taking out the pairs:
- \(\sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\)
Let's look at another example for further clarity:
Find the square root of 50 using the prime factorization method:
- Factorize 50 into its prime factors:
- \(50 = 2 \times 5 \times 5\)
- Pair the prime factors:
- \(50 = (5 \times 5) \times 2\)
- Simplify by taking out the pairs:
- \(\sqrt{50} = \sqrt{(5 \times 5) \times 2} = 5\sqrt{2}\)
By following these steps, you can simplify any square root using the prime factorization method. This method is particularly useful for simplifying square roots of numbers that are not perfect squares.
Solved Examples
| Number | Prime Factors | Simplified Square Root |
|---|---|---|
| 8 | \(2 \times 2 \times 2\) | \(2\sqrt{2}\) |
| 81 | \(3 \times 3 \times 3 \times 3\) | \(3 \times 3 = 9\) |
| 324 | \(2 \times 2 \times 3 \times 3 \times 3 \times 3\) | \(2 \times 3 \times 3 = 18\) |
Simplifying Fractions under Square Roots
When simplifying fractions that contain square roots, the process involves two main steps: simplifying the square root and rationalizing the denominator. Let's go through these steps in detail.
Step 1: Simplify the Square Root
The first step is to simplify the square root in both the numerator and the denominator, if possible. This involves breaking down the number inside the square root into its prime factors and extracting any perfect squares.
- Identify any perfect squares within the square root. For example, \( \sqrt{18} \) can be simplified as follows:
- \( \sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2} \)
- Apply this to both the numerator and the denominator. For example, to simplify \( \sqrt{\frac{72}{50}} \):
- First, simplify each part: \( \sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2} \) and \( \sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2} \).
- Then, the fraction becomes \( \frac{6\sqrt{2}}{5\sqrt{2}} \).
Step 2: Rationalize the Denominator
To rationalize the denominator means to eliminate any square roots in the denominator. This is done by multiplying both the numerator and the denominator by the conjugate of the denominator.
- For example, to rationalize \( \frac{5}{\sqrt{3}} \):
- Multiply the numerator and the denominator by \( \sqrt{3} \): \( \frac{5}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{5\sqrt{3}}{3} \).
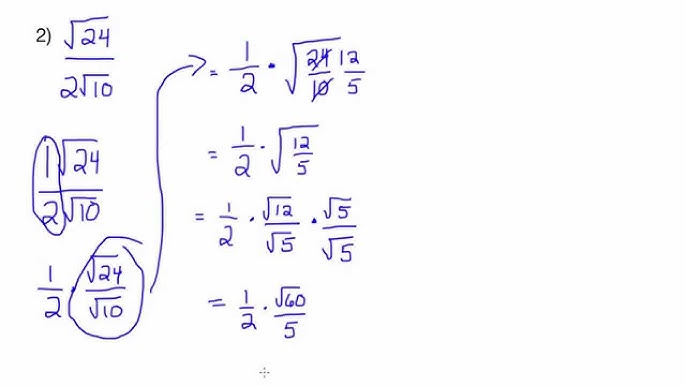
- For a more complex example, \( \frac{\sqrt{30}}{\sqrt{50}} \):
- First, simplify the square roots: \( \frac{\sqrt{30}}{\sqrt{50}} = \frac{\sqrt{30}}{\sqrt{25 \times 2}} = \frac{\sqrt{30}}{5\sqrt{2}} \).
- Then rationalize the denominator: \( \frac{\sqrt{30}}{5\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{60}}{10} = \frac{\sqrt{4 \times 15}}{10} = \frac{2\sqrt{15}}{10} = \frac{\sqrt{15}}{5} \).
Examples and Practice
Here are some examples to help you practice simplifying fractions under square roots:
- Simplify \( \frac{\sqrt{8}}{2} \):
- \( \sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2} \)
- So, \( \frac{2\sqrt{2}}{2} = \sqrt{2} \).
- Simplify \( \frac{3}{\sqrt{5}} \):
- Multiply by the conjugate: \( \frac{3}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{3\sqrt{5}}{5} \).
By practicing these steps, you can simplify fractions with square roots efficiently and accurately. Remember, the key is to simplify the square root first and then rationalize the denominator.
Step-by-Step Guide to Simplification
Simplifying square roots within fractions involves a systematic approach to reduce the expression to its simplest form. Follow these steps to simplify fractions under square roots effectively:
-
Simplify the Square Root:
Identify and simplify any square roots in the fraction. Look for perfect square factors within the radicand (the number under the square root) and simplify them.
- Example: Simplify \( \sqrt{72} \)
\( \sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2} \)
- Example: Simplify \( \sqrt{72} \)
-
Rationalize the Denominator:
If the denominator contains a square root, multiply both the numerator and the denominator by the conjugate of the denominator to eliminate the square root.
- Example: Simplify \( \frac{5}{\sqrt{3}} \)
\( \frac{5}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{5\sqrt{3}}{3} \)
- Example: Simplify \( \frac{5}{\sqrt{3}} \)
-
Combine and Simplify:
Once the square roots are simplified and the denominator is rationalized, check if the resulting fraction can be simplified further.
- Example: Simplify \( \frac{\sqrt{18}}{3} \)
\( \sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2} \)
\( \frac{3\sqrt{2}}{3} = \sqrt{2} \)
- Example: Simplify \( \frac{\sqrt{18}}{3} \)
-
Practice Problems:
Try these additional examples to practice simplifying fractions with square roots:
- Simplify \( \frac{\sqrt{50}}{\sqrt{2}} \)
\( \sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2} \)
\( \frac{5\sqrt{2}}{\sqrt{2}} = 5 \)
- Simplify \( \frac{1}{\sqrt{3}} \)
\( \frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3} \)
- Simplify \( \frac{\sqrt{50}}{\sqrt{2}} \)
By following these steps and practicing regularly, you can simplify square roots within fractions more confidently and accurately.

Separating Numerator and Denominator
When simplifying fractions under square roots, it's essential to handle the numerator and denominator separately. This process often involves using the Quotient Property of Square Roots, which states that:
Here is a step-by-step guide to separating the numerator and the denominator:
-
Identify the Fraction: Begin with the fraction that needs simplification. For instance:
-
Simplify the Numerator: Simplify the square root in the numerator by factoring out perfect squares. For example:
-
Rewrite the Fraction: After simplifying the numerator, rewrite the fraction with the simplified square root:
-
Rationalize the Denominator (if necessary): If there is a square root in the denominator, rationalize it by multiplying the numerator and the denominator by the conjugate or appropriate form. For example:
By following these steps, you can simplify fractions under square roots, ensuring that the expression is in its simplest form.
Simplifying the Numerator
When simplifying the numerator of a fraction under a square root, follow these steps:
- Factor the Numerator: Identify the prime factors of the numerator.
- For example, if the numerator is 18, its prime factors are \(2 \times 3^2\).
- Apply the Square Root to Each Factor: Use the property that the square root of a product is the product of the square roots.
- \(\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2}\)
- Simplify Perfect Squares: Simplify any perfect squares under the square root.
- \(\sqrt{3^2} = 3\), so \(\sqrt{18} = \sqrt{2} \times 3 = 3\sqrt{2}\)
- Write the Simplified Form: Combine the simplified factors.
- The simplified form of \(\sqrt{18}\) is \(3\sqrt{2}\).
By following these steps, you can simplify the numerator of any fraction under a square root.
Simplifying the Denominator
When simplifying the denominator of a fraction under a square root, the goal is to eliminate the square root in the denominator. This process is called rationalizing the denominator. Here are the steps to simplify the denominator:
- Identify the square root in the denominator.
- If the denominator is a single square root (monomial), multiply both the numerator and the denominator by the same square root to remove the square root from the denominator.
- Multiply the numerator and the denominator by \( \sqrt{2} \):
- \( \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \)
- If the denominator is a binomial containing a square root (e.g., \( a + \sqrt{b} \)), multiply both the numerator and the denominator by the conjugate of the denominator. The conjugate of \( a + \sqrt{b} \) is \( a - \sqrt{b} \).
- Multiply the numerator and the denominator by the conjugate \( 3 - \sqrt{2} \):
- \( \frac{1}{3 + \sqrt{2}} \times \frac{3 - \sqrt{2}}{3 - \sqrt{2}} = \frac{3 - \sqrt{2}}{(3)^2 - (\sqrt{2})^2} \)
- Simplify the denominator using the difference of squares formula:
- \( = \frac{3 - \sqrt{2}}{9 - 2} = \frac{3 - \sqrt{2}}{7} \)
For example, to simplify \( \frac{1}{\sqrt{2}} \):
For example, to simplify \( \frac{1}{3 + \sqrt{2}} \):
Following these steps will help you rationalize the denominator, ensuring that the fraction is in its simplest form.
Combining Simplified Results
Once you have simplified both the numerator and the denominator of a fraction under a square root, the next step is to combine these simplified results. Here’s how to do it:
-
Use the Quotient Property of Square Roots
The quotient property states that the square root of a fraction is the same as the fraction of the square roots of the numerator and the denominator:
\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\]
For example, to simplify \(\sqrt{\frac{18}{32}}\), first simplify the fraction inside the radical:
\[\frac{18}{32} = \frac{9}{16}\]
Then apply the quotient property:
\[\sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4}\]
-
Rationalize the Denominator
If the denominator contains a square root, multiply both the numerator and the denominator by the conjugate of the denominator to eliminate the square root. For example, to simplify \(\frac{5}{\sqrt{3}}\):
\[\frac{5}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{5\sqrt{3}}{3}\]
-
Simplify the Expression
Combine the simplified numerator and denominator to get the final result. If you end up with a fraction where both the numerator and denominator are simplified square roots, the expression is already in its simplest form. For example:
\[\sqrt{\frac{18}{50}} = \frac{\sqrt{18}}{\sqrt{50}} = \frac{3\sqrt{2}}{5\sqrt{2}} = \frac{3}{5}\]
By following these steps, you can simplify complex fractions with square roots in both the numerator and the denominator effectively.

Rationalizing the Denominator
Rationalizing the denominator involves eliminating any radicals present in the denominator of a fraction. This process ensures that the denominator is a rational number, making the expression simpler and easier to work with. Here are detailed steps to rationalize the denominator:
- Identify the Radical in the Denominator:
First, determine if the denominator contains a square root or other radical. For example, consider the fraction:
\(\dfrac{1}{\sqrt{2}}\). - Multiply by the Radical:
To eliminate the radical, multiply both the numerator and the denominator by the same radical. This uses the property that \(\sqrt{a} \cdot \sqrt{a} = a\). For our example:
\[\dfrac{1}{\sqrt{2}} \cdot \dfrac{\sqrt{2}}{\sqrt{2}} = \dfrac{\sqrt{2}}{2}.\] - Simplify the Result:
After multiplying, simplify the expression if possible. In this case, the denominator is now rational, so the expression is simplified.
Rationalizing Denominators with Binomials
When the denominator is a binomial containing a radical, multiply by its conjugate. The conjugate of \(a + b\sqrt{c}\) is \(a - b\sqrt{c}\), and vice versa. This process uses the difference of squares formula:
Consider the fraction: \(\dfrac{1}{3 + \sqrt{2}}\).
- Find the Conjugate:
The conjugate of \(3 + \sqrt{2}\) is \(3 - \sqrt{2}\).
- Multiply by the Conjugate:
Multiply both the numerator and the denominator by this conjugate:
\[\dfrac{1}{3 + \sqrt{2}} \cdot \dfrac{3 - \sqrt{2}}{3 - \sqrt{2}} = \dfrac{3 - \sqrt{2}}{(3 + \sqrt{2})(3 - \sqrt{2})}.\] - Apply the Difference of Squares Formula:
Expand the denominator using the difference of squares:
\[(3 + \sqrt{2})(3 - \sqrt{2}) = 3^2 - (\sqrt{2})^2 = 9 - 2 = 7.\]
The expression becomes:
\[\dfrac{3 - \sqrt{2}}{7}.\] - Simplify:
The final rationalized form is:
\[\dfrac{3 - \sqrt{2}}{7}.\]
These steps ensure that the denominator is rationalized, making the expression simpler and more manageable.
Common Mistakes to Avoid
When simplifying square roots with fractions, it's important to be aware of common mistakes that can lead to incorrect results. Here are some of the most frequent errors and how to avoid them:
- Not Fully Simplifying the Square Root: Always simplify the square root completely before proceeding with other steps. For instance, simplify
- Forgetting to Rationalize the Denominator: A common mistake is leaving a square root in the denominator. To rationalize, multiply the numerator and denominator by the conjugate of the denominator or by the same square root. For example,
- Incorrect Factorization: Ensure correct factorization of the number under the square root. For example, factor
- Mixing Numerator and Denominator Operations: Perform operations on the numerator and denominator separately unless they are being combined after simplification. For example, simplify
- Omitting Conjugate Multiplication: When rationalizing denominators with binomials, multiply by the conjugate to eliminate the square root. For example, with a denominator of , use to simplify correctly.
By being mindful of these common mistakes, you can ensure your simplifications of square roots in fractions are accurate and efficient.
Practice Problems and Solutions
Sharpen your skills in simplifying square roots with fractions through these practice problems. Solutions are provided to help you verify your answers and understand the process of simplification in detail.
-
Problem 1: Simplify \(\frac{\sqrt{50}}{\sqrt{2}}\)
Solution: Factor \(\sqrt{50}\) into \(\sqrt{25 \cdot 2} = 5\sqrt{2}\). Then, \(\frac{5\sqrt{2}}{\sqrt{2}} = 5\).
-
Problem 2: Simplify \(\frac{1}{\sqrt{3}}\)
Solution: Rationalize the denominator by multiplying the numerator and denominator by \(\sqrt{3}\), resulting in \(\frac{\sqrt{3}}{3}\).
-
Problem 3: Simplify \(\frac{\sqrt{18} + \sqrt{2}}{\sqrt{9}}\)
Solution: Simplify \(\sqrt{18}\) to \(3\sqrt{2}\) and \(\sqrt{9}\) to \(3\). The expression becomes \(\frac{3\sqrt{2} + \sqrt{2}}{3} = \frac{4\sqrt{2}}{3}\).
-
Problem 4: Simplify \(\sqrt{\frac{4}{9}}\)
Solution: The square root of 4 is 2, and the square root of 9 is 3. Therefore, \(\sqrt{\frac{4}{9}}\) simplifies to \(\frac{2}{3}\).
-
Problem 5: Simplify \(\frac{4}{\sqrt{18}}\)
Solution: Simplify \(\sqrt{18}\) to \(3\sqrt{2}\). Rationalize the denominator: \(\frac{4}{\sqrt{18}} = \frac{4 \cdot \sqrt{18}}{18} = \frac{2\sqrt{2}}{3}\).
Practicing these problems will help reinforce your understanding of simplifying square roots in fractions. Remember to simplify the square roots as much as possible and rationalize the denominator when necessary.
Advanced Techniques
When simplifying square roots of fractions, advanced techniques can make the process more efficient and effective. Here are several strategies to consider:
-
Prime Factorization:
Break down both the numerator and the denominator into their prime factors. This can help in identifying and simplifying square roots within the fraction.
- Factorize the numerator and the denominator.
- Simplify the square roots of the factors.
- Reconstruct the fraction using the simplified square roots.
-
Using Conjugates for Rationalization:
When you encounter a square root in the denominator, multiply both the numerator and the denominator by the conjugate of the denominator to eliminate the square root.
- Identify the conjugate of the denominator. For example, if the denominator is \( \sqrt{a} + \sqrt{b} \), its conjugate is \( \sqrt{a} - \sqrt{b} \).
- Multiply the numerator and the denominator by this conjugate.
- Apply the distributive property (FOIL method) to simplify the result.
- Simplify the resulting expression by combining like terms.
-
Applying the Distributive Property:
For fractions involving algebraic expressions, apply the distributive property to simplify the expression inside the square root before attempting to simplify the fraction.
- Expand the algebraic expressions inside the square root.
- Simplify the expanded expressions where possible.
- Simplify the square roots of the resulting expressions.
-
Leveraging the Pythagorean Identity:
In cases involving trigonometric functions, use the Pythagorean identity to simplify square roots of fractions by converting them into trigonometric terms that are easier to manage.
- Express the trigonometric functions in terms of their identities.
- Simplify the resulting expressions.
- Apply square roots to the simplified trigonometric expressions.
-
Utilizing Complex Numbers:
For square roots of negative fractions, consider using complex numbers. Represent the square root of a negative number as an imaginary number (\(i\)).
- Express the negative fraction in terms of its imaginary components.
- Simplify the imaginary components separately.
- Combine the simplified components to form the final expression.
These advanced techniques require a solid foundation in algebra and arithmetic but offer powerful tools for simplifying complex fractions with square roots. Mastery of these methods enhances problem-solving skills and mathematical understanding.
Applications of Simplified Square Roots
Understanding the applications of simplified square roots is essential in various fields, from geometry to physics. Here, we explore some common real-world uses:
1. Geometry and Area Calculation
One of the most direct applications of square roots is in calculating the side length of a square when the area is known. For instance, if the area of a square is \(A\) square units, the side length \(s\) can be found using the formula:
\[ s = \sqrt{A} \]
Example: If a square has an area of 36 square units, the side length is:
\[ s = \sqrt{36} = 6 \text{ units} \]
2. Physics and Gravity
In physics, the time \(t\) it takes for an object to fall from a certain height \(h\) can be calculated using the formula:
\[ t = \sqrt{\frac{2h}{g}} \]
where \(g\) is the acceleration due to gravity (approximately \(9.8 \, m/s^2\) on Earth). This application helps in determining how long it takes for an object to hit the ground when dropped from a specific height.
Example: If an object is dropped from a height of 20 meters, the time it takes to reach the ground is:
\[ t = \sqrt{\frac{2 \times 20}{9.8}} \approx 2.02 \text{ seconds} \]
3. Engineering and Construction
Engineers often use square roots in design and construction, particularly when dealing with areas and volumes. For example, calculating the diagonal of a square or rectangle involves the Pythagorean theorem:
\[ d = \sqrt{l^2 + w^2} \]
where \(l\) and \(w\) are the length and width of the rectangle, and \(d\) is the diagonal.
Example: For a rectangle with a length of 3 meters and width of 4 meters, the diagonal is:
\[ d = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{ meters} \]
4. Accident Investigations
In accident investigations, the speed of a vehicle before a crash can be estimated by analyzing skid marks. The formula used often involves square roots:
\[ v = \sqrt{30 \times d \times f} \]
where \(v\) is the speed in miles per hour, \(d\) is the length of the skid marks in feet, and \(f\) is the coefficient of friction.
Example: If skid marks are 50 feet long and the coefficient of friction is 0.7, the speed is:
\[ v = \sqrt{30 \times 50 \times 0.7} \approx 32.4 \text{ mph} \]
5. Biology and Medicine
In biology and medicine, square roots are used to calculate various indices and rates. For example, the body surface area (BSA) in medical dosing can be estimated using the Mosteller formula:
\[ \text{BSA} = \sqrt{\frac{height \, (cm) \times weight \, (kg)}{3600}} \]
This helps in determining the correct dosage of medication for a patient based on their body surface area.
Conclusion
From designing buildings to analyzing accidents and medical applications, simplified square roots play a crucial role in various real-world scenarios. Understanding these applications highlights the importance of mastering square root simplification techniques.
Conclusion
In this guide, we have explored the various methods and principles for simplifying square roots involving fractions. From understanding the basic properties of square roots to applying techniques such as prime factorization and rationalizing the denominator, each step has been detailed to provide a comprehensive understanding.
Simplifying square roots, especially with fractions, can initially seem daunting. However, by breaking down the process into manageable steps, it becomes more accessible. Key takeaways include:
- Understanding Properties: Grasping the fundamental properties of square roots and fractions is essential.
- Prime Factorization: Using prime factorization to simplify square roots helps in reducing complex expressions into simpler forms.
- Rationalizing the Denominator: Ensuring the denominator is free of radicals by multiplying by a suitable form of 1.
- Combining Simplified Results: Properly combining the simplified parts of the numerator and denominator.
- Advanced Techniques: Exploring more complex methods and applications for a deeper understanding.
With practice, the process of simplifying square roots with fractions will become more intuitive. Remember to avoid common mistakes such as misapplying the properties of square roots or incorrect factorization. Continual practice with various problems will build your confidence and skill in this area.
By mastering these techniques, you will not only excel in simplifying square roots with fractions but also enhance your overall mathematical problem-solving abilities. Keep practicing, and use the methods outlined in this guide to simplify square root expressions effectively.
Video này hướng dẫn cách đơn giản hóa phân số dưới dấu căn với các thủ thuật toán học để giúp bạn giải quyết các vấn đề phức tạp một cách dễ dàng.
Đơn giản hóa phân số dưới dấu căn - Thủ thuật toán học
READ MORE:
Video này hướng dẫn cách đơn giản hóa căn bậc hai của phân số với các phương pháp như sqrt(a/b) và a/sqrt(b) để giúp bạn dễ dàng giải các bài toán phức tạp.
Đơn giản hóa căn bậc hai của phân số: sqrt(a/b), a/sqrt(b)