Topic simplify square roots worksheet: Welcome to our comprehensive guide on simplifying square roots. This article provides detailed worksheets and exercises designed to help students understand and master the process of simplifying square roots, from basic concepts to advanced techniques. Whether you're preparing for exams or just looking to improve your math skills, these resources will guide you every step of the way.
Table of Content
- Simplifying Square Roots Worksheets
- Introduction to Simplifying Square Roots
- Basic Concepts of Square Roots
- Understanding Perfect Squares
- Methods for Simplifying Square Roots
- Prime Factorization Method
- Using the Division Method
- Simplifying Square Roots of Non-Perfect Squares
- Combining Like Terms with Square Roots
- Rationalizing the Denominator
- Practice Problems: Simplifying Square Roots
- Step-by-Step Solutions
- Common Mistakes and How to Avoid Them
- Advanced Simplification Techniques
- Simplifying Square Roots with Variables
- Applying Simplification in Real-World Problems
- Worksheets for Different Grade Levels
- Printable Simplify Square Roots Worksheets
- Interactive Simplify Square Roots Exercises
- YOUTUBE:
Simplifying Square Roots Worksheets
Simplifying square roots can be a fun and engaging way to improve your math skills. Below are some resources and examples to help you understand and practice this concept.
Understanding Square Roots
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, \( \sqrt{9} = 3 \) because \( 3 \times 3 = 9 \).
Basic Rule for Simplifying Square Roots
When simplifying square roots, the key rule to remember is:
\[ \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \]
For instance, to simplify \( \sqrt{12} \):
\[ 12 = 4 \times 3 \]
\[ \sqrt{12} = \sqrt{4 \times 3} \]
\[ = \sqrt{4} \times \sqrt{3} \]
\[ = 2\sqrt{3} \]
Examples
Here are a few more examples to illustrate the process:
- Simplify \( \sqrt{45} \):
\[ 45 = 9 \times 5 \]
\[ \sqrt{45} = \sqrt{9 \times 5} \]
\[ = \sqrt{9} \times \sqrt{5} \]
\[ = 3\sqrt{5} \] - Simplify \( \sqrt{18} \):
\[ 18 = 9 \times 2 \]
\[ \sqrt{18} = \sqrt{9 \times 2} \]
\[ = \sqrt{9} \times \sqrt{2} \]
\[ = 3\sqrt{2} \]
Simplifying Fractions
To simplify the square root of a fraction, simplify the numerator and the denominator separately, and then simplify the whole fraction if necessary:
\[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
For example, to simplify \( \sqrt{\frac{30}{10}} \):
\[ \sqrt{\frac{30}{10}} = \sqrt{3} \]
Worksheets
Here are some printable worksheets to practice simplifying square roots:
Additional Resources
For more practice, you can explore these additional resources:

READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots is a fundamental skill in mathematics that involves reducing a square root to its simplest form. The process typically involves expressing the number inside the square root as the product of a perfect square and another factor. Understanding and memorizing perfect squares, as well as mastering techniques like prime factorization and the division method, can greatly aid in this process.
- Perfect Squares: Numbers like 1, 4, 9, 16, 25, and 36 are perfect squares because their square roots are integers (e.g., √16 = 4).
- Prime Factorization: Breaking down the number inside the square root into its prime factors helps simplify the square root. For instance, √48 can be simplified by expressing 48 as 16 × 3, and then simplifying to 4√3.
- Division Method: This method involves dividing the number inside the square root by the largest perfect square factor. It’s especially useful for non-perfect squares.
By practicing these methods, students can become proficient in simplifying both perfect and non-perfect square roots. This knowledge is essential for tackling more complex mathematical problems and is widely applicable in various real-world scenarios.
Basic Concepts of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the symbol √.
Key concepts:
- Definition: The square root of a number x, denoted as √x, is a number y such that y * y = x.
- Non-negative: The square root of a non-negative number is always a non-negative number.
- Perfect Squares: Numbers like 1, 4, 9, 16, etc., have exact integer square roots.
- Radical Symbol: The symbol √ is called the radical symbol, indicating a square root operation.
- Rational Numbers: Square roots can be rational (like √4 = 2) or irrational (like √2).
Understanding square roots is fundamental in mathematics for solving equations, simplifying expressions, and analyzing geometric shapes.
Understanding Perfect Squares
Perfect squares are integers that are the squares of other integers. They have whole number square roots.
Key points:
- Definition: A perfect square is a number that can be expressed as the square of an integer.
- Examples:
- 1 is a perfect square because √1 = 1.
- 4 is a perfect square because √4 = 2.
- 9 is a perfect square because √9 = 3.
- 16 is a perfect square because √16 = 4.
- 25 is a perfect square because √25 = 5.
- Properties:
- The square root of a perfect square is always an integer.
- Perfect squares are used in various mathematical concepts including algebra, geometry, and number theory.
- Applications: Understanding perfect squares helps in simplifying square roots, solving equations, and calculating areas of squares.
Methods for Simplifying Square Roots
There are several methods to simplify square roots efficiently:
- Prime Factorization Method:
Factorize the number inside the square root into prime factors, then group pairs of identical factors and bring them out of the square root as their square root.
- Using the Division Method:
Divide the number inside the square root by the largest perfect square possible, then simplify the resulting expression.
- Rationalizing Denominators:
For square roots in denominators, multiply the numerator and the denominator by the conjugate of the denominator to eliminate the square root from the denominator.
- Combining Like Terms:
When adding or subtracting terms with square roots, ensure they have the same radicand (number inside the square root) before combining.

Prime Factorization Method
The prime factorization method is a systematic approach to simplifying square roots:
- Step 1: Factorize the number inside the square root into its prime factors.
- Step 2: Pair up identical factors.
- Step 3: Bring each pair of identical factors out of the square root as their square root.
- Step 4: Multiply any remaining factors inside the square root that cannot be paired.
Example:
Simplify √72:
- Prime factorization of 72: 72 = 2 * 2 * 2 * 3 * 3 = 2^3 * 3^2.
- Pair up identical factors: √72 = √(2^3 * 3^2).
- Bring out pairs: √72 = 2 * 3 * √(3) = 6√3.
Using the Division Method
The division method simplifies square roots by dividing the number inside the square root by the largest perfect square:
- Step 1: Identify the largest perfect square that divides the number inside the square root.
- Step 2: Divide the number inside the square root by this perfect square.
- Step 3: Simplify the resulting expression.
Example:
Simplify √48:
- Identify the largest perfect square: The largest perfect square that divides 48 is 16 (since √16 = 4).
- Divide 48 by 16: √48 = √(16 * 3) = √16 * √3 = 4√3.
Simplifying Square Roots of Non-Perfect Squares
Non-perfect squares are numbers whose square roots are not integers. Simplifying square roots of non-perfect squares involves:
- Step 1: Factorize the number inside the square root into its prime factors.
- Step 2: Identify any perfect square factors.
- Step 3: Bring out the square roots of perfect squares from under the radical sign.
- Step 4: Leave non-perfect square factors under the radical sign.
Example:
Simplify √20:
- Prime factorization of 20: 20 = 2 * 2 * 5 = 2^2 * 5.
- Identify perfect square factors: √20 = √(4 * 5) = √4 * √5 = 2√5.
Combining Like Terms with Square Roots
When combining like terms with square roots, follow these steps:
- Step 1: Identify terms with the same radicand (number under the square root).
- Step 2: Add or subtract the coefficients of these terms.
- Step 3: Keep the radicand unchanged under the square root.
Example:
Combine like terms in the expression 3√2 + 2√2:
- Identify terms with the same radicand (2).
- Add the coefficients: 3 + 2 = 5.
- Keep the radicand unchanged: 5√2.
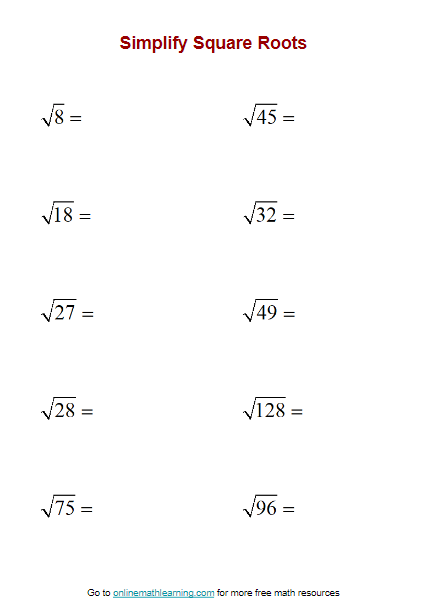
Rationalizing the Denominator
Rationalizing the denominator involves eliminating square roots from the denominator of a fraction:
- Step 1: Multiply both the numerator and the denominator by the conjugate of the denominator.
- Step 2: Simplify the resulting expression.
Example:
Rationalize the denominator of the fraction 1 / √3:
- Multiply numerator and denominator by √3: 1 / √3 * √3 / √3 = √3 / 3.
Practice Problems: Simplifying Square Roots
Practice solving these problems to master simplifying square roots:
- Simplify √18.
- Simplify √75.
- Simplify √48.
- Simplify √27.
- Simplify √50.
Step-by-Step Solutions
Follow these steps to solve square root problems:
- Step 1: Factorize the number inside the square root into its prime factors.
- Step 2: Identify any perfect square factors.
- Step 3: Bring out the square roots of perfect squares from under the radical sign.
- Step 4: Multiply any remaining factors inside the square root that cannot be paired.
Apply these steps to each practice problem to find the simplified square root.
Common Mistakes and How to Avoid Them
When simplifying square roots, avoid these common errors to ensure accuracy:
- Incorrectly identifying perfect squares. Verify if a number is a perfect square before simplifying.
- Forgetting to simplify radicals fully. Always simplify the square root expression as much as possible.
- Misunderstanding the difference between perfect squares and non-perfect squares. Use proper methods for each case.
- Skipping steps in the simplification process. Follow each step carefully to avoid mistakes.
- Rationalizing the denominator incorrectly. Understand when and how to rationalize properly.
- Confusing addition and multiplication of square roots. Apply the correct operations according to mathematical rules.
- Not using parentheses correctly with variables. Ensure clarity by correctly grouping terms.
- Ignoring the domain restrictions. Consider the domain of the original expression when simplifying.
- Overlooking the application of simplification techniques in real-world problems. Practice applying concepts to various scenarios.

Advanced Simplification Techniques
In this section, we will explore advanced techniques for simplifying square roots that go beyond the basic methods. These techniques will help you tackle more complex square root problems efficiently.
1. Simplifying Radicals Using Prime Factorization
The prime factorization method involves breaking down the radicand into its prime factors and then simplifying. Follow these steps:
- Find the prime factors of the radicand.
- Group the prime factors into pairs.
- For each pair, take one number out of the square root.
- Multiply the numbers outside the square root.
- Leave any unpaired prime factors inside the square root.
Example: Simplify \( \sqrt{72} \)
- Prime factors of 72: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \)
- Group pairs: \( (2 \times 2), (3 \times 3), 2 \)
- Simplify: \( \sqrt{72} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \)
2. Rationalizing the Denominator
When a square root appears in the denominator, it is often useful to rationalize it. This process involves eliminating the square root from the denominator.
- Multiply both the numerator and the denominator by the conjugate of the denominator.
- Simplify the expression by multiplying out the terms.
- Combine like terms and simplify the square roots.
Example: Rationalize \( \frac{3}{\sqrt{5}} \)
- Multiply by the conjugate: \( \frac{3}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{3\sqrt{5}}{5} \)
3. Using the Product and Quotient Rules
The product and quotient rules for square roots can simplify the process:
- Product Rule: \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \)
- Quotient Rule: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)
These rules help break down complex radicals into simpler parts that can be individually simplified.
4. Simplifying Nested Radicals
Nesting occurs when a square root is within another square root. Simplify nested radicals using the following steps:
- Identify the inner and outer radicals.
- Simplify the inner radical first, if possible.
- Simplify the outer radical using the simplified inner radical.
Example: Simplify \( \sqrt{3 + 2\sqrt{2}} \)
- Use the formula \( \sqrt{a + b} = \sqrt{a} + \sqrt{b} \) to simplify nested radicals when applicable.
5. Applying Advanced Techniques to Variables
When dealing with square roots that contain variables, the same principles apply. Ensure all variables are in their simplest form:
- Simplify the coefficients and variable parts separately.
- Use prime factorization and the product rule as needed.
Example: Simplify \( \sqrt{50x^4} \)
- Prime factorize: \( 50 = 2 \times 5 \times 5 \)
- Simplify: \( \sqrt{50x^4} = \sqrt{25 \times 2 \times x^4} = 5x^2\sqrt{2} \)
Conclusion
These advanced techniques for simplifying square roots will enable you to handle more complex mathematical problems with confidence. Practice these methods regularly to master the art of simplification.
Simplifying Square Roots with Variables
Simplifying square roots with variables follows similar rules to simplifying square roots of numbers, but with added steps for handling the variables. Here’s a step-by-step guide to help you through the process.
Step-by-Step Process
- Identify Perfect Squares: Break down the variable expressions into products of perfect squares. For instance, \( x^4 \) is a perfect square because it can be written as \( (x^2)^2 \).
- Separate Variables and Numbers: If you have an expression like \( \sqrt{16x^4} \), separate the number and the variable: \( \sqrt{16} \cdot \sqrt{x^4} \).
- Simplify the Numerical Part: Simplify the square root of the numerical part. For example, \( \sqrt{16} = 4 \).
- Simplify the Variable Part: Apply the square root to the variable part by halving the exponent: \( \sqrt{x^4} = x^2 \).
- Combine the Results: Multiply the simplified numerical part by the simplified variable part: \( \sqrt{16x^4} = 4x^2 \).
Examples
- Example 1: Simplify \( \sqrt{36x^6} \)
- Break down: \( \sqrt{36} \cdot \sqrt{x^6} \)
- Simplify: \( 6 \cdot x^3 \)
- Result: \( 6x^3 \)
- Example 2: Simplify \( \sqrt{49x^8y^2} \)
- Break down: \( \sqrt{49} \cdot \sqrt{x^8} \cdot \sqrt{y^2} \)
- Simplify: \( 7 \cdot x^4 \cdot y \)
- Result: \( 7x^4y \)
- Example 3: Simplify \( \sqrt{50x^3} \)
- Break down: \( \sqrt{25 \cdot 2} \cdot \sqrt{x^2 \cdot x} \)
- Simplify: \( 5\sqrt{2} \cdot x \sqrt{x} \)
- Result: \( 5x\sqrt{2x} \)
Combining Like Terms
When simplifying expressions with multiple terms, combine like terms if possible. For example:
- Simplify \( \sqrt{4x^2} + \sqrt{9x^2} \):
- Simplify each term: \( 2x + 3x \)
- Combine like terms: \( 5x \)
Special Cases
For variables with odd exponents, separate the variable into even and odd parts. For example:
- Simplify \( \sqrt{x^5} \):
- Rewrite as \( \sqrt{x^4 \cdot x} \)
- Simplify: \( x^2\sqrt{x} \)
By following these steps, you can simplify square roots that contain variables effectively, making complex algebraic expressions more manageable.
Applying Simplification in Real-World Problems
Simplifying square roots is not just an academic exercise; it has practical applications in various real-world scenarios. Here are a few examples demonstrating how simplification can be used to solve real-life problems effectively:
-
Construction and Architecture:
When calculating the dimensions of a triangular roof truss, you may need to use the Pythagorean theorem. For instance, if the sides of the triangle are \(a = 6\) meters and \(b = 8\) meters, you can find the hypotenuse \(c\) by simplifying \(\sqrt{a^2 + b^2}\). Thus, \(c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10\) meters.
-
Physics and Engineering:
In physics, calculating the resultant force when two perpendicular forces are applied can involve square roots. For example, if one force is 3 Newtons and the other is 4 Newtons, the resultant force \(R\) is \(\sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\) Newtons.
-
Finance and Economics:
When determining the standard deviation of a dataset in statistics, square roots are essential. If the variance of the dataset is 16, the standard deviation is \(\sqrt{16} = 4\). Simplifying square roots helps in making the data interpretation more straightforward.
-
Medicine and Pharmacology:
Dosage calculations for medications often involve square roots. For example, the body surface area (BSA) of a patient, which is used to determine the correct dosage of certain drugs, can be estimated using the square root formula: \(BSA = \sqrt{\text{height (cm)} \times \text{weight (kg)}/3600}\).
-
Agriculture:
Farmers use square roots to determine the area of their fields. For instance, if a square plot of land has an area of 2500 square meters, the length of one side of the plot is \(\sqrt{2500} = 50\) meters, simplifying the planning and division of the land.
By mastering the simplification of square roots, you can apply these skills to solve practical problems across various fields, enhancing your analytical and problem-solving abilities in real-world situations.
Worksheets for Different Grade Levels
Providing grade-specific worksheets for simplifying square roots can help students at different learning stages develop a strong understanding of the concept. Below are some suggestions for worksheets tailored to various grade levels:
Grade 4
Introduction to Square Roots: Simple exercises that introduce the concept of square roots and perfect squares.
Identifying Perfect Squares: Worksheets that focus on identifying perfect squares up to 100.
Grade 5
Basic Simplification: Worksheets that help students practice simplifying square roots of perfect squares.
Square Roots and Estimation: Exercises that involve estimating square roots of numbers that are not perfect squares.
Grade 6
Finding Square Roots: Worksheets that require students to find the square roots of numbers up to 400.
Square Roots of Fractions: Introducing the concept of finding the square roots of simple fractions.
Grade 7
Advanced Simplification: More complex exercises involving the simplification of non-perfect squares.
Square Roots of Decimals: Worksheets that help students practice finding and simplifying the square roots of decimal numbers.
Grade 8
Mixed Operations: Worksheets that combine square roots with other operations like addition, subtraction, multiplication, and division.
Real-World Applications: Exercises that apply the concept of square roots to real-world problems and scenarios.
High School (Algebra 1 and 2)
Complex Numbers: Introducing the concept of square roots of negative numbers and complex numbers.
Quadratic Equations: Solving quadratic equations that involve square roots.
These worksheets are designed to provide comprehensive practice and enhance understanding at each grade level. They include a variety of problems, from basic identification and simplification to more complex real-world applications, ensuring a thorough grasp of square root concepts.

Printable Simplify Square Roots Worksheets
These printable worksheets are designed to help students practice and master the simplification of square roots. The worksheets are available for various grade levels and cover a range of topics from basic to advanced concepts.
- Basic Simplification:
- Identifying perfect squares
- Breaking down composite numbers
- Practice with simple numbers
- Intermediate Simplification:
- Simplifying square roots of larger numbers
- Using prime factorization
- Combining like terms
- Advanced Simplification:
- Simplifying square roots with variables
- Rationalizing denominators
- Complex expressions involving square roots
Each worksheet includes step-by-step instructions and plenty of examples to ensure thorough understanding. These printable resources are perfect for classroom use or for extra practice at home.
Examples of Available Worksheets:
| Includes 47 scaffolded questions covering various aspects of radical simplification. | |
| Focuses on breaking numbers into factors and simplifying the square roots. | |
| Covers identifying radicands, converting forms, and reducing radicals to their simplest form. |
These worksheets are freely available to download in PDF format, making it easy for students to practice and improve their skills in simplifying square roots.
Interactive Simplify Square Roots Exercises
Interactive exercises offer a dynamic and engaging way to practice simplifying square roots. Here are some exciting activities and games that can help students reinforce their understanding:
-
Square Root Concentration Game
Match square roots with their corresponding values by flipping cards. This game improves memory and quick recall of square root values.
-
MathPup Hook Square Root
Guide a bouncing ball to hit the correct answer bubble for square root questions. This game enhances fine motor skills and hand-eye coordination.
-
Simplifying Square Roots Quiz
Solve problems involving irrational square roots and surds. This quiz helps clarify the difference between simple and complex square roots.
-
Matching Game - Square Roots
Match numbers with their square roots in a grid. This game helps improve speed and accuracy in calculating square roots.
-
Square Roots Spin the Wheel
Spin the wheel to get a square root question and select the correct answer from multiple choices. This game adds an element of fun competition to learning.
-
Printable Interactive Worksheets
Combine traditional practice with interactive elements by using worksheets that include QR codes or links to online games. This method bridges hands-on practice with digital engagement.
These interactive exercises make learning square roots more enjoyable and effective, helping students to grasp the concepts through practice and play.
Cách Đơn Giản Hóa Căn Bậc Hai
READ MORE:
Video hướng dẫn đơn giản hóa căn bậc hai từ Toán Học Vui, hấp dẫn và dễ hiểu cho người xem.
Toán Học Vui - Đơn Giản Hóa Căn Bậc Hai