Topic 60 square root simplified: Discover the simplified square root of 60, explained in an easy-to-understand way. This article will guide you through the process of finding and simplifying √60, using prime factorization and perfect squares, and understanding its properties. Perfect for students and math enthusiasts looking to deepen their knowledge!
Table of Content
- Results for "60 square root simplified"
- Introduction to Square Root of 60
- Understanding Square Roots
- Definition and Properties of Square Root of 60
- Step-by-Step Simplification of √60
- Prime Factorization Method
- Simplifying Using Perfect Squares
- Calculating the Decimal Value of √60
- Is 60 a Perfect Square?
- Rational or Irrational: Understanding √60
- Square Root of 60 in Different Forms
- FAQs on Square Root of 60
- Practical Examples Involving √60
- Using Technology to Calculate √60
- YOUTUBE:
Results for "60 square root simplified"
The square root of 60 simplified can be represented as:
| Exact Value: | \(\sqrt{60} = 2\sqrt{15}\) |
| Approximate Decimal: | \(\sqrt{60} \approx 7.745966692414834\) |
| Factors: | Prime factorization of 60: \(2^2 \times 3 \times 5\) |
Thus, the simplified form of \(\sqrt{60}\) is \(2\sqrt{15}\).

READ MORE:
Introduction to Square Root of 60
The square root of 60, denoted as √60, is a number which when multiplied by itself equals 60. In its simplified radical form, √60 can be expressed as 2√15. This simplification is achieved by breaking down 60 into its prime factors and identifying perfect squares. Understanding the square root of 60 involves recognizing its properties, its decimal value, and its relevance in various mathematical contexts. By exploring both manual calculation methods and technological tools, one can gain a comprehensive understanding of √60.
Understanding Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 9 is 3, because 3 x 3 = 9. This concept is essential in mathematics, particularly in algebra and geometry.
Square roots can be represented using the radical symbol (√). For example, √25 = 5. It’s important to note that every positive number has two square roots: one positive and one negative, as both (5 x 5) and (-5 x -5) result in 25.
There are perfect squares, which are the squares of whole numbers. Examples include:
- √4 = 2
- √9 = 3
- √16 = 4
- √25 = 5
Calculating square roots of non-perfect squares can be challenging, but methods such as factorization, long division, and using a calculator can help. For example, the square root of 60 can be simplified to 2√15, and its approximate decimal value is 7.746.
Understanding square roots is crucial for solving quadratic equations, analyzing geometric shapes, and working with various algebraic expressions. With practice, you can master the techniques to simplify and calculate square roots effectively.
Definition and Properties of Square Root of 60
The square root of 60, denoted as \(\sqrt{60}\), is a number that, when multiplied by itself, equals 60. It can be expressed in both exact and decimal forms.
Here are the key properties of the square root of 60:
- Exact Form: \(\sqrt{60}\) can be simplified by breaking down 60 into its prime factors. The prime factorization of 60 is \(2^2 \cdot 3 \cdot 5\). Thus, \(\sqrt{60} = \sqrt{2^2 \cdot 3 \cdot 5} = 2\sqrt{15}\).
- Decimal Form: The square root of 60 in decimal form is approximately \(7.746\).
- Product Property: The square root of a product is the product of the square roots of each factor: \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\). For example, \(\sqrt{60} = \sqrt{4 \cdot 15} = \sqrt{4} \cdot \sqrt{15} = 2 \cdot \sqrt{15}\).
- Quotient Property: The square root of a fraction is the quotient of the square roots of the numerator and the denominator: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
Understanding these properties helps in simplifying and working with the square root of 60 in various mathematical contexts.
Step-by-Step Simplification of √60
To simplify the square root of 60, we follow these steps:
- Identify the factors of 60. The prime factorization of 60 is 2 × 2 × 3 × 5.
- Group the factors into pairs of identical numbers, if possible. In this case, 60 can be written as 22 × 3 × 5.
- Apply the square root to the prime factors: \[ \sqrt{60} = \sqrt{2^2 \times 3 \times 5} \]
- Simplify by taking the square root of the paired factors: \[ \sqrt{2^2} \times \sqrt{3} \times \sqrt{5} = 2 \times \sqrt{3 \times 5} \]
- Combine the simplified terms: \[ 2 \sqrt{15} \]
Thus, the simplified form of the square root of 60 is 2√15.
Prime Factorization Method
The prime factorization method is a straightforward approach to simplify the square root of a number. Here, we will simplify the square root of 60 using this method.
-
Factorize 60 into its prime factors:
To begin, we need to factorize 60 into its prime factors. We do this by dividing 60 by the smallest prime number until we cannot divide anymore.
60 ÷ 2 = 30 30 ÷ 2 = 15 15 ÷ 3 = 5 5 ÷ 5 = 1 Therefore, the prime factors of 60 are 2, 2, 3, and 5. This can be written as:
\[ 60 = 2^2 \times 3 \times 5 \]
-
Group the prime factors in pairs:
Next, we group the prime factors in pairs. In this case, \( 2^2 \) forms a pair while 3 and 5 do not pair with any other factors.
-
Apply the square root to each group:
We take the square root of each pair and leave the unpaired factors under the square root sign:
\[ \sqrt{60} = \sqrt{2^2 \times 3 \times 5} = \sqrt{2^2} \times \sqrt{3 \times 5} \]
-
Simplify the square roots:
The square root of \( 2^2 \) is 2. Therefore, we can simplify the expression to:
\[ \sqrt{60} = 2 \times \sqrt{15} \]
-
Final result:
The simplified form of the square root of 60 is:
\[ \sqrt{60} = 2\sqrt{15} \]
By using the prime factorization method, we have simplified \(\sqrt{60}\) to \(2\sqrt{15}\). This method helps in breaking down the number into its prime factors, making it easier to handle square roots.
Simplifying Using Perfect Squares
Simplifying the square root of 60 using perfect squares involves breaking down the number into its prime factors and then grouping the factors into pairs of perfect squares. Here is a step-by-step guide:
-
Find the prime factors of 60:
- 60 can be factored into 2, 2, 3, and 5.
- This can be written as \(60 = 2^2 \times 3 \times 5\).
-
Identify the perfect squares:
- The perfect square factor here is \(2^2\).
-
Separate the perfect squares from the other factors:
- This can be expressed as \(\sqrt{60} = \sqrt{2^2 \times 3 \times 5}\).
-
Take the square root of the perfect square:
- \(\sqrt{2^2} = 2\).
-
Combine the results:
- \(\sqrt{60} = \sqrt{2^2 \times 3 \times 5} = 2 \sqrt{3 \times 5}\).
- This simplifies to \(2 \sqrt{15}\).
Therefore, the simplified form of \(\sqrt{60}\) using perfect squares is \(2 \sqrt{15}\).
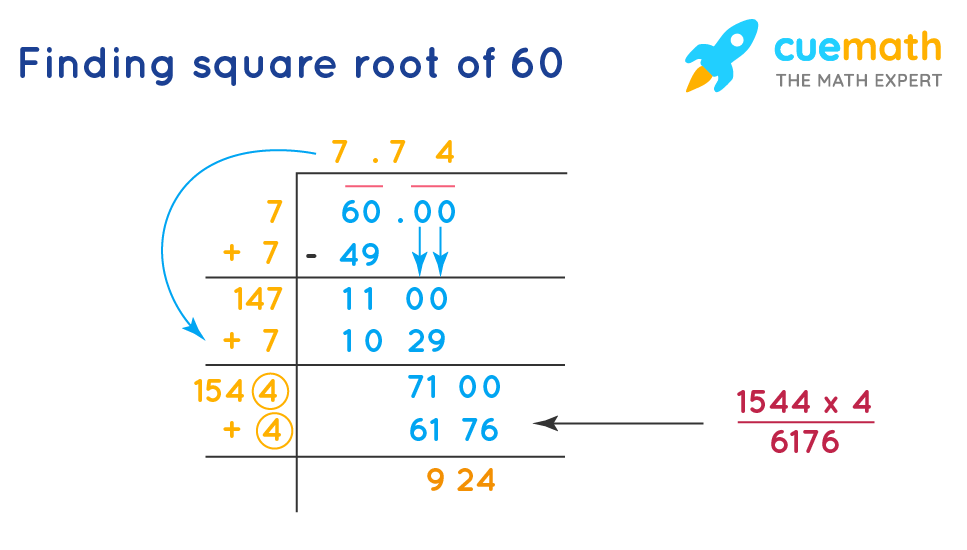
Calculating the Decimal Value of √60
The square root of 60 can be calculated to a decimal value using various methods. One common method is the long division technique. Here is a step-by-step guide on how to find the decimal value of √60:
-
First, write the number 60 as follows:
\[60.000000\]
-
Group the digits in pairs from the decimal point towards the left and right:
\[6 | 00 | 00 | 00\]
-
Find the largest number whose square is less than or equal to the first group (6). The number is 2 (since \(2^2 = 4\)). Write 2 above the 6 and subtract \(2^2\) from 6 to get 2:
\[6 - 4 = 2\]
-
Bring down the next pair of digits (00) to get 200. Double the number in the quotient (2) to get 4. Find a digit (d) such that \((40 + d) \cdot d \leq 200\). The digit is 4 (since \(44 \cdot 4 = 176\)). Write 4 in the quotient:
\[200 - 176 = 24\]
-
Bring down the next pair of zeros to get 2400. Double the current quotient (24) to get 48. Find a digit (d) such that \((480 + d) \cdot d \leq 2400\). The digit is 4 (since \(484 \cdot 4 = 1936\)). Write 4 in the quotient:
\[2400 - 1936 = 464\]
-
Continue the process until you reach the desired decimal places. In this case, to two decimal places, we get:
\[7.74\]
Thus, the square root of 60, calculated using the long division method, is approximately:
\[\sqrt{60} \approx 7.7459666\]
This decimal value confirms that the square root of 60 is an irrational number because it cannot be expressed as a simple fraction and has a non-terminating decimal expansion.
Is 60 a Perfect Square?
A perfect square is a number that can be expressed as the square of an integer. To determine if 60 is a perfect square, we need to see if its square root is an integer.
Let's examine the square root of 60:
\[\sqrt{60}\]
We can simplify this expression to determine if it's a perfect square.
- Prime factorize 60: \(60 = 2 \times 2 \times 3 \times 5\)
- Group the prime factors into pairs: \(\sqrt{60} = \sqrt{2^2 \times 3 \times 5}\)
- Separate the pairs from the non-paired factors: \(\sqrt{2^2} \times \sqrt{3 \times 5}\)
- Simplify the paired factors: \(2 \times \sqrt{15}\)
The simplified form is \(2\sqrt{15}\), where \(\sqrt{15}\) is not an integer. Therefore, \(\sqrt{60}\) is not an integer.
Since \(\sqrt{60}\) is not an integer, 60 is not a perfect square.
In conclusion, 60 cannot be expressed as the square of an integer, which means it is not a perfect square.

Rational or Irrational: Understanding √60
To determine whether the square root of 60 (√60) is rational or irrational, we first need to understand what makes a number rational or irrational:
- Rational Number: A number that can be expressed as a fraction of two integers (a/b) where b is not zero.
- Irrational Number: A number that cannot be expressed as a simple fraction; its decimal form is non-repeating and non-terminating.
Now, let's examine √60:
The prime factorization of 60 is:
60 = 2 × 2 × 3 × 5
Taking the square root of both sides, we get:
√60 = √(2 × 2 × 3 × 5) = √(2² × 15) = 2√15
Here, 2 is a rational number, but √15 is not a perfect square and cannot be simplified further to a rational number. The decimal representation of √15 is non-repeating and non-terminating, which makes it irrational.
Since √15 is irrational, 2√15 is also irrational because the product of a rational number (2) and an irrational number (√15) is irrational.
Therefore, the square root of 60 (√60) is an irrational number.
Square Root of 60 in Different Forms
The square root of 60 can be represented in several forms, each useful in different mathematical contexts. Let's explore these various forms:
- Radical Form: The most common representation is the radical form, expressed as √60.
- Simplified Radical Form: By breaking down 60 into its prime factors, we get:
√60 = √(4 × 15) = √4 × √15 = 2√15
Thus, the simplified radical form is 2√15.
- Decimal Form: Using a calculator, we can find the approximate decimal value of the square root of 60:
√60 ≈ 7.746
This value is rounded to three decimal places.
- Exponential Form: The square root of 60 can also be written using fractional exponents:
√60 = 601/2
Each of these forms is useful depending on the context in which the square root is being used. The radical form is often used in algebraic expressions, the simplified form is useful for further simplifications, the decimal form is helpful for approximate calculations, and the exponential form is used in more advanced mathematical contexts.
FAQs on Square Root of 60
- What is the square root of 60?
The square root of 60 is approximately \( \sqrt{60} \approx 7.746 \).
- Is 60 a perfect square?
No, 60 is not a perfect square because its square root is not an integer. A perfect square has an integer as its square root.
- Is the square root of 60 rational or irrational?
The square root of 60 is an irrational number because it cannot be expressed as a simple fraction.
- Can the square root of 60 be simplified?
Yes, the square root of 60 can be simplified to \( 2\sqrt{15} \).
- How do you calculate the square root of 60?
You can calculate the square root of 60 using a calculator or using the long division method. On most calculators, you can simply type in 60 and press the square root button to get \( \sqrt{60} \approx 7.746 \).
- What is the square root of 60 as a fraction?
Since \( \sqrt{60} \) is an irrational number, it cannot be expressed exactly as a fraction. However, it can be approximated as \( \frac{7746}{1000} \), which simplifies to \( \frac{3873}{500} \).
- How do you express the square root of 60 with an exponent?
The square root of 60 can be written with an exponent as \( 60^{1/2} \).
- What are some practical applications of the square root of 60?
The square root of 60 can be used in various real-life applications, such as calculating dimensions in construction, solving geometry problems, and in scientific calculations where precise measurements are required.
Practical Examples Involving √60
Understanding the practical applications of the square root of 60 (√60) can enhance your grasp of mathematical concepts. Here are a few examples:
-
Example 1: Calculating the Area of a Rectangle
John, a salesman, wants to build a rectangular floor garage to store goods for his shop. He wants the floor to be 20 feet long and 10√60 feet wide. If the cost to paint the floor is $2 per square foot, how much will it cost?
Solution:
- Length of the floor = 20 feet
- Width of the floor = 10√60 feet
- Area of the floor = Length × Width = 20 × 10√60 = 200√60
- Approximate value of √60 ≈ 7.746
- Area ≈ 200 × 7.746 = 1549.2 square feet
- Cost to paint = Area × $2 = 1549.2 × 2 = $3098.4
-
Example 2: Travel Distance Calculation
A car travels at a speed of 6√240 miles per hour. How far will it travel in 2 hours?
Solution:
- Speed of the car = 6√240 miles per hour
- Time = 2 hours
- Distance = Speed × Time = 6√240 × 2 = 12√240
- Prime factorization of 240 = 2² × 2 × 2 × 3 × 5 = 4 × 60
- √240 = 2√60
- Distance = 12 × 2√60 = 24√60
- Approximate value of √60 ≈ 7.746
- Distance ≈ 24 × 7.746 = 185.9 miles
-
Example 3: Side Length of an Equilateral Triangle
If the area of an equilateral triangle is 60√3 square inches, find the length of one side of the triangle.
Solution:
- Area of an equilateral triangle = (√3/4) × a², where 'a' is the side length
- Given area = 60√3
- 60√3 = (√3/4) × a²
- a² = (60√3 × 4)/√3 = 240
- a = √240 = 2√60
- Approximate value of √60 ≈ 7.746
- Side length, a ≈ 2 × 7.746 = 15.492 inches

Using Technology to Calculate √60
Modern technology provides various tools to simplify and calculate the square root of 60 quickly and accurately. Here, we explore different methods and devices that can assist in this calculation.
Using a Calculator
Most scientific calculators come with a square root function, making it straightforward to find the square root of 60:
- Turn on your calculator.
- Enter the number 60.
- Press the √ (square root) button.
- The display will show approximately 7.746.
Some advanced calculators may provide options to see more decimal places or even the simplified radical form, which in this case is \(2\sqrt{15}\).
Using Computer Software
Computers and mobile devices can also be used to calculate square roots through software like Excel, Google Sheets, or specialized math applications:
- Open Excel or Google Sheets.
- In any cell, type
=SQRT(60)and press Enter. - The cell will display the result, approximately 7.746.
Similarly, math-focused applications like Symbolab or Wolfram Alpha can be used for these calculations. For instance, entering sqrt(60) in Symbolab will yield the simplified result \(2\sqrt{15}\) and its decimal approximation.
Online Calculators
Numerous online calculators can compute the square root of 60 efficiently:
- Visit websites like Omni Calculator or Visual Fractions.
- Enter the number 60 in the input field.
- Click the calculate button to get the result \(2\sqrt{15}\) or approximately 7.746.
Mobile Apps
Several mobile apps designed for math calculations can help with finding square roots:
- Microsoft Math Solver: Enter or scan the number 60, and the app will show \(2\sqrt{15}\) and the decimal value.
- Photomath: Take a picture of the problem, and the app will provide a step-by-step solution.
Practical Applications
Understanding and utilizing technology to calculate square roots can be extremely beneficial in various fields such as engineering, architecture, and data analysis. With the aid of calculators, software, and apps, complex mathematical computations become much more manageable.
Đơn giản hóa căn bậc hai của 60: Căn(60)
READ MORE:
Học về căn bậc hai và căn bậc ba với Thầy J, bao gồm các ví dụ minh họa và giải thích chi tiết.
Căn Bậc Hai và Căn Bậc Ba | Toán Học với Thầy J











