Topic square root of 18 radical form: Discover how to simplify the square root of 18 into its radical form. This comprehensive guide breaks down the process step-by-step, showing you how to transform √18 into 3√2. Whether you're a student or a math enthusiast, you'll find clear explanations and practical tips for mastering radical expressions.
Table of Content
- Understanding the Square Root of 18 in Radical Form
- Introduction to Square Roots
- Understanding the Square Root of 18
- Simplifying the Square Root of 18
- Methods to Simplify Radical Expressions
- Expressing √18 in Radical Form
- Step-by-Step Simplification Process
- Finding Perfect Square Factors
- Breaking Down √18: Factor Tree Method
- Exact vs. Approximate Values of √18
- Applications of Simplified Square Roots
- Visualizing Square Root Simplification
- Comparison with Other Square Roots
- Common Misconceptions in Simplification
- Practical Uses of Square Roots in Math and Science
- Further Reading and Practice Problems
- Conclusion and Summary
- YOUTUBE: Video hướng dẫn cách đơn giản hóa căn bậc hai của 18: Sqrt(18) giúp bạn hiểu rõ và áp dụng đúng phương pháp.
Understanding the Square Root of 18 in Radical Form
The square root of 18, represented as √18, can be simplified into its radical form. This involves expressing the square root in the simplest possible way.
Simplifying √18
To simplify √18, we look for the largest perfect square factor of 18. Here are the steps:
- Identify the factors of 18. The factors are 1, 2, 3, 6, 9, and 18.
- Find the largest perfect square among these factors. The perfect squares are numbers like 1, 4, 9, 16, etc. The largest perfect square factor of 18 is 9.
- Rewrite 18 as the product of 9 and 2: \(18 = 9 \times 2\).
- Use the property of square roots that \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \). Thus, \( \sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} \).
- Simplify \( \sqrt{9} \) to 3, since \( 9 = 3^2 \). Therefore, \( \sqrt{18} = 3 \times \sqrt{2} \).
So, the simplified form of √18 is \( 3 \sqrt{2} \).
Square Root in Different Forms
The square root of 18 can be expressed in different forms:
- Decimal form: The approximate decimal value of \( \sqrt{18} \) is about 4.2426.
- Exact form: In exact radical form, it is \( 3 \sqrt{2} \).
Why Simplify Square Roots?
Simplifying square roots can make calculations easier and helps in solving algebraic equations where square roots are involved. It also gives a clearer understanding of the value in its simplest form.
Visual Representation
The process of simplification can be visualized as breaking down the number 18 into its factors and then taking the square root of the largest perfect square factor:
| Number | Factors | Perfect Square Factors |
| 18 | 1, 2, 3, 6, 9, 18 | 1, 9 |
| √18 | \( \sqrt{9 \times 2} \) | \( 3 \sqrt{2} \) |
By understanding the process, you can simplify square roots more easily and accurately.

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics, providing a basis for various complex mathematical operations. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because \(3 \times 3 = 9\).
Square roots are represented using the radical symbol (√). The number under the radical symbol is called the radicand. For instance, in √18, 18 is the radicand.
Square roots can be categorized into two types:
- Perfect Square Roots: These are square roots of perfect squares, such as 1, 4, 9, 16, etc. Their square roots are whole numbers (e.g., √16 = 4).
- Non-Perfect Square Roots: These are square roots of numbers that are not perfect squares, such as 2, 3, 5, 18, etc. Their square roots are irrational numbers, which cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal expansions (e.g., √18 ≈ 4.2426).
Understanding how to simplify square roots, especially those of non-perfect squares, is an essential skill in algebra and higher mathematics. This guide will help you grasp the methods and steps to simplify the square root of 18 and express it in its radical form.
Understanding the Square Root of 18
The square root of a number is a value that, when multiplied by itself, gives the original number. For 18, the square root is written as √18. To understand the square root of 18, it's important to recognize both its radical form and its simplified form.
In mathematics, the square root of 18 can be expressed in its radical form as follows:
\(\sqrt{18}\)
To simplify this, we look for the largest perfect square factor of 18. The number 18 can be factored into its prime components:
- 18 = 2 × 9
- 9 is a perfect square (3 × 3)
Using this factorization, we can rewrite the square root of 18:
\(\sqrt{18} = \sqrt{2 \times 9}\)
Since 9 is a perfect square, we know \(\sqrt{9} = 3\). This allows us to further simplify the expression:
\(\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}\)
Thus, the simplified form of \(\sqrt{18}\) is \(3\sqrt{2}\). This means that the square root of 18 can be expressed as 3 times the square root of 2.
Additionally, we can find the approximate decimal value of \(\sqrt{18}\). Using a calculator, we find:
\(\sqrt{18} \approx 4.2426\)
This value is useful in practical applications where an approximate value is sufficient. However, for exact mathematical work, we use the simplified radical form \(3\sqrt{2}\).
In summary, understanding the square root of 18 involves recognizing its radical form \(\sqrt{18}\), simplifying it to \(3\sqrt{2}\), and knowing its approximate decimal value. This comprehension allows us to work with the square root of 18 in various mathematical contexts.
Simplifying the Square Root of 18
To simplify \( \sqrt{18} \), we begin by identifying perfect square factors of 18. This helps in expressing \( \sqrt{18} \) in its simplest radical form.
- Recognize that 18 can be factored into prime factors: \( 18 = 2 \times 3^2 \).
- Take out the perfect square factor from under the square root: \( \sqrt{18} = \sqrt{2 \times 9} \).
- Split the square root into two separate square roots: \( \sqrt{2 \times 9} = \sqrt{2} \times \sqrt{9} \).
- Since \( \sqrt{9} = 3 \), substitute to get the final result: \( \sqrt{18} = 3\sqrt{2} \).
Therefore, \( \sqrt{18} \) simplifies to \( 3\sqrt{2} \).
Methods to Simplify Radical Expressions
There are several methods to simplify radical expressions like \( \sqrt{18} \). Here are some common approaches:
- Factorization Method: Factor the number inside the square root into its prime factors.
- Perfect Square Method: Identify and pull out perfect square factors from under the square root.
- Estimation Method: Use estimation techniques to approximate the value of the square root.
- Rationalizing Denominators: For expressions involving square roots in the denominator, multiply by the conjugate to eliminate the square root.
- Using Factor Trees: Construct a factor tree to break down the number into prime factors, facilitating simplification.

Expressing √18 in Radical Form
To express \( \sqrt{18} \) in radical form, follow these steps:
- Identify the prime factors of 18: \( 18 = 2 \times 3^2 \).
- Separate the perfect square factor from under the square root: \( \sqrt{18} = \sqrt{2 \times 9} \).
- Split the square root into two separate radicals: \( \sqrt{2 \times 9} = \sqrt{2} \times \sqrt{9} \).
- Since \( \sqrt{9} = 3 \), substitute to get the final result: \( \sqrt{18} = 3\sqrt{2} \).
Therefore, \( \sqrt{18} \) in radical form is \( 3\sqrt{2} \).
Step-by-Step Simplification Process
Here is a step-by-step process to simplify \( \sqrt{18} \):
- Start with the number under the square root, 18.
- Identify its prime factors: \( 18 = 2 \times 3^2 \).
- Take out the perfect square factor from under the square root: \( \sqrt{18} = \sqrt{2 \times 9} \).
- Split the square root into two separate radicals: \( \sqrt{2 \times 9} = \sqrt{2} \times \sqrt{9} \).
- Since \( \sqrt{9} = 3 \), substitute to get the final result: \( \sqrt{18} = 3\sqrt{2} \).
Therefore, \( \sqrt{18} \) simplifies step-by-step to \( 3\sqrt{2} \).
Finding Perfect Square Factors
When finding perfect square factors of \( \sqrt{18} \), follow these steps:
- Start with the number under the square root, 18.
- Identify its prime factors: \( 18 = 2 \times 3^2 \).
- Look for perfect square factors among the prime factors.
- In this case, \( 9 \) is a perfect square because \( 9 = 3^2 \).
- Take out the perfect square factor from under the square root: \( \sqrt{18} = \sqrt{2 \times 9} \).
- Split the square root into two separate radicals: \( \sqrt{2 \times 9} = \sqrt{2} \times \sqrt{9} \).
- Since \( \sqrt{9} = 3 \), substitute to get the final result: \( \sqrt{18} = 3\sqrt{2} \).
Therefore, the perfect square factor in \( \sqrt{18} \) is \( 9 \), and \( \sqrt{18} \) simplifies to \( 3\sqrt{2} \).
Breaking Down √18: Factor Tree Method
Using the factor tree method to break down \( \sqrt{18} \) involves the following steps:
- Start with the number under the square root, 18.
- Find two factors of 18, such as 2 and 9.
- Continue factoring each number until you reach prime factors.
- Factor 9 into \( 3 \times 3 \).
- Combine the factors to rewrite \( \sqrt{18} \) as \( \sqrt{2 \times 3 \times 3} \).
- Split the square root into individual square roots: \( \sqrt{2 \times 3 \times 3} = \sqrt{2} \times \sqrt{3} \times \sqrt{3} \).
- Since \( \sqrt{3 \times 3} = 3 \), the final result is \( \sqrt{18} = 3\sqrt{2} \).
Therefore, using the factor tree method, \( \sqrt{18} \) simplifies to \( 3\sqrt{2} \).
Exact vs. Approximate Values of √18
The exact value of \( \sqrt{18} \) is \( 3\sqrt{2} \).
Approximately, \( \sqrt{18} \approx 4.24 \).
Applications of Simplified Square Roots
Simplified square roots, such as \( 3\sqrt{2} \) for \( \sqrt{18} \), find various applications in mathematics and real-world scenarios:
- Geometry: Simplified square roots are used in calculating dimensions of shapes and figures.
- Engineering: Engineers use simplified square roots for measurements and calculations involving dimensions and structures.
- Physics: Simplified square roots are fundamental in physics equations, such as in calculations involving forces and energies.
- Finance: In financial modeling, simplified square roots may be used in risk analysis and interest rate calculations.
- Computer Graphics: Simplified square roots help in programming algorithms for rendering and animation.
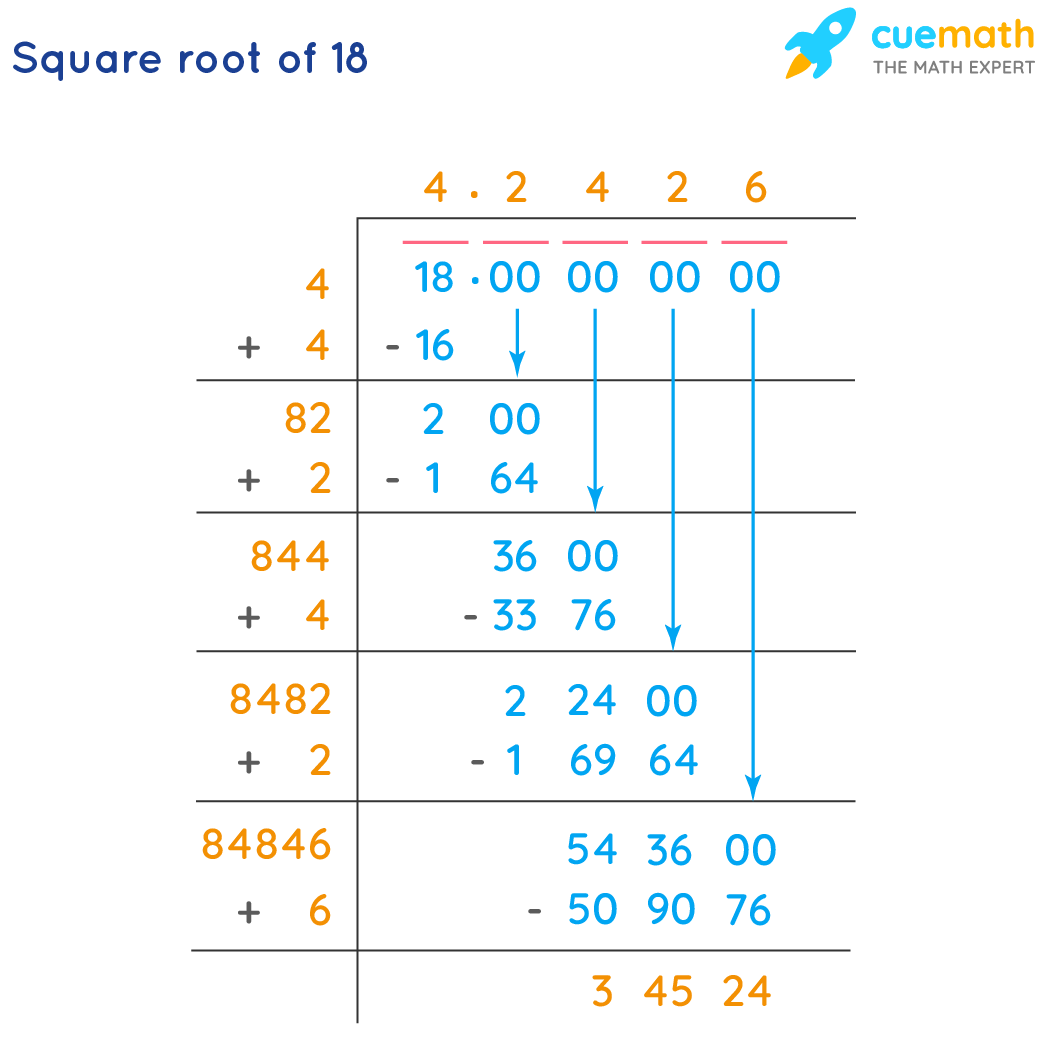
Visualizing Square Root Simplification
Understanding the simplification of the square root of 18 can be greatly aided by visualizing the process. Here we will break down the steps using visual aids and MathJax for clear mathematical representation.
Step-by-Step Simplification
To simplify √18, we follow these steps:
- Factorize 18 into its prime factors:
\[ 18 = 2 \times 9 \]
And since \( 9 = 3 \times 3 \), we can write:
\[ 18 = 2 \times 3 \times 3 \]
- Rewrite under the square root:
\[ \sqrt{18} = \sqrt{2 \times 3^2} \]
- Separate the square root:
\[ \sqrt{18} = \sqrt{2} \times \sqrt{3^2} \]
- Simplify further:
\[ \sqrt{18} = \sqrt{2} \times 3 \]
\[ \sqrt{18} = 3\sqrt{2} \]
Visual Representation Using a Factor Tree
Creating a factor tree helps in visualizing the factorization process:
- Start with 18.
- Break it down into 2 and 9.
- Further break down 9 into 3 and 3.
Thus, the factor tree looks like this:
18
|
2 9
|
3 3
Graphical Visualization
A graph can help to better understand the relationship between the exact value and its approximate decimal form:
- The exact form: \( 3\sqrt{2} \)
- The approximate form: 4.24
This shows how close the simplified radical form is to its decimal approximation.
Comparative Visualization
To grasp how √18 compares with other square roots:
| Number | Square Root (Simplified) | Approximate Value |
|---|---|---|
| √16 | 4 | 4.00 |
| √18 | 3√2 | 4.24 |
| √20 | 2√5 | 4.47 |
By comparing, we see that 3√2 falls between √16 and √20, illustrating its approximate value and position on the number line.
Comparison with Other Square Roots
Understanding how the square root of 18 compares with other square roots helps in grasping its relative magnitude and properties. Below is a detailed comparison with other common square roots.
- Perfect Squares: The closest perfect squares to 18 are 16 and 25.
- \(\sqrt{16} = 4\)
- \(\sqrt{25} = 5\)
- Simple Radical Form: Some other square roots in their simplified radical forms include:
- \(\sqrt{8} = 2\sqrt{2}\)
- \(\sqrt{12} = 2\sqrt{3}\)
- \(\sqrt{20} = 2\sqrt{5}\)
To visualize this comparison, consider a number line where we plot these square roots. Here, \(\sqrt{18}\) is represented as \(3\sqrt{2}\), which lies between 4 and 5.
| Square Root | Value |
|---|---|
| \(\sqrt{16}\) | 4 |
| \(\sqrt{18}\) | \(3\sqrt{2} \approx 4.24\) |
| \(\sqrt{25}\) | 5 |
Comparing \(\sqrt{18}\) with other non-perfect squares:
- \(\sqrt{10} \approx 3.16\)
- \(\sqrt{18} \approx 4.24\)
- \(\sqrt{20} \approx 4.47\)
Through these comparisons, it is clear that \(\sqrt{18}\) is larger than \(\sqrt{16}\) and \(\sqrt{10}\), but smaller than \(\sqrt{20}\) and \(\sqrt{25}\). This helps us understand its relative size and its place among other common square roots.
Additionally, understanding the properties of \(\sqrt{18}\) in relation to these other square roots can provide insight into their use in various mathematical contexts, such as solving equations, calculating distances, and other applications where radical simplifications are necessary.
Common Misconceptions in Simplification
When simplifying square roots, especially those involving numbers like 18, there are several common misconceptions that can lead to errors. Understanding and addressing these misconceptions is crucial for accurate mathematical work. Below, we explore these misunderstandings and provide clarifications.
-
Misconception: The square root of a non-perfect square cannot be simplified.
Many students believe that if a number is not a perfect square, its square root cannot be simplified. However, non-perfect squares can often be simplified by factoring out perfect squares within them. For example, √18 can be simplified because 18 = 9 × 2, and 9 is a perfect square.
Correct simplification of √18:
\(\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}\)
-
Misconception: Simplified radicals must result in whole numbers.
Some students expect that after simplification, the result should be a whole number. This is not true for most non-perfect squares. The result of simplifying a radical often includes a coefficient and a remaining square root. For instance, simplifying √18 results in 3√2, which is not a whole number.
-
Misconception: Only integers can be perfect square factors.
Another common misconception is that only whole numbers can be perfect squares. While whole numbers are perfect squares (e.g., 1, 4, 9, 16), it is essential to recognize that any number multiplied by itself is a perfect square. However, in the context of simplifying radicals, we usually deal with integer perfect squares.
-
Misconception: The order of multiplication inside the square root does not matter.
While the commutative property of multiplication states that the order of factors does not affect the product, it is important to identify and extract perfect square factors correctly. For example, in simplifying √18, recognizing 9 as a perfect square is key to correctly simplifying the expression.
-
Misconception: Simplification changes the value of the expression.
Simplification of radicals does not change the value of the expression; it only changes its form to make it more manageable or insightful. For example, √18 and 3√2 are numerically equivalent, but 3√2 is the simplified form.
Practical Uses of Square Roots in Math and Science
Square roots are fundamental in various fields of math and science. Here, we will explore some practical applications where the square root of a number, such as √18, plays a crucial role.
1. Geometry
In geometry, square roots are used to calculate distances and lengths. For example:
- Pythagorean Theorem: In a right triangle, the length of the hypotenuse (c) can be found using the formula \( c = \sqrt{a^2 + b^2} \). If one leg of the triangle is 3 units and the other is 3√2 units, the hypotenuse will be \( c = \sqrt{(3)^2 + (3\sqrt{2})^2} = \sqrt{9 + 18} = \sqrt{27} = 3\sqrt{3} \).
- Area and Perimeter Calculations: The diagonal of a square with side length a is given by \( a\sqrt{2} \). For a square with a side length of 3 units, the diagonal is \( 3\sqrt{2} \) units.
2. Physics
Square roots are prevalent in physics, especially in equations dealing with energy, motion, and waves.
- Kinetic Energy: The formula for kinetic energy is \( KE = \frac{1}{2}mv^2 \). To find the velocity (v) when the kinetic energy and mass are known, the square root is used: \( v = \sqrt{\frac{2KE}{m}} \).
- Wave Speed: The speed of a wave (v) on a string is given by \( v = \sqrt{\frac{T}{\mu}} \), where T is the tension in the string and μ is the linear mass density. If T is 18 N/m and μ is 2 kg/m, the speed is \( v = \sqrt{\frac{18}{2}} = \sqrt{9} = 3 \) m/s.
3. Engineering
Square roots are used in various engineering calculations, such as stress analysis and signal processing.
- Stress Analysis: In engineering, the stress (σ) on a material can be calculated using the formula \( \sigma = \frac{F}{A} \), where F is the force applied, and A is the area. When calculating the resulting deformations, square roots often appear in the equations, especially when dealing with complex geometries.
- Signal Processing: The RMS (root mean square) value of a signal is a statistical measure of the magnitude of a varying quantity. It is calculated using the formula \( RMS = \sqrt{\frac{1}{N} \sum_{i=1}^{N} x_i^2} \), where \( x_i \) are the individual measurements and N is the number of measurements.
4. Computer Science
Square roots are used in algorithms and data analysis.
- Euclidean Distance: In computer science, the Euclidean distance between two points in a plane is computed using the formula \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \). For points (1, 2) and (4, 6), the distance is \( d = \sqrt{(4-1)^2 + (6-2)^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \).
- Machine Learning: In clustering algorithms such as k-means, the square root function is used to calculate the distance between data points and cluster centroids.
Understanding and applying square roots, such as √18, are essential in solving real-world problems across various domains of math and science.
Further Reading and Practice Problems
To deepen your understanding of square roots, including the square root of 18, explore the following resources and practice problems. These materials will help reinforce concepts and provide opportunities to apply what you have learned.
- Understanding Square Roots: A comprehensive guide on the properties of square roots, methods of simplification, and applications in various fields.
- Simplifying Radicals: Learn the techniques to simplify radicals, such as factoring out perfect squares and using the product rule for radicals.
Practice Problems
- Simplify the following radical expressions:
- √50
- √75
- √32
- Find the exact and approximate values of these square roots:
- √20
- √45
- √72
- Solve these application problems:
- If the area of a square is 18 square units, what is the length of one side?
- A right triangle has one leg of length 3 units and a hypotenuse of length √18 units. Find the length of the other leg.
- Compare the side lengths of two squares with areas 18 and 32 square units, respectively.
Interactive Learning and Further Exploration
- - Interactive exercises to practice simplifying and calculating square roots.
- - Step-by-step solutions for simplifying √18 and other similar problems.
- - Detailed explanations and examples for understanding and simplifying the square root of 18.
- - In-depth guide and challenging questions related to the square root of 18.
Conclusion and Summary
The square root of 18, denoted as \(\sqrt{18}\), simplifies to \(3\sqrt{2}\). This form is derived by recognizing that 18 can be factored into \(9 \times 2\), and since the square root of 9 is 3, we simplify \(\sqrt{18}\) to \(3\sqrt{2}\).
Understanding the process of simplifying square roots, such as \(\sqrt{18}\), is a fundamental aspect of mathematics. It involves breaking down the number into its prime factors, grouping them in pairs, and simplifying the radicals.
Throughout this guide, we have explored the concept of square roots, the methods to simplify them, and their practical applications in various fields of math and science. We have also addressed common misconceptions and provided tools and techniques for further practice and study.
- We started with an introduction to square roots and their properties.
- We delved into the specific case of \(\sqrt{18}\), demonstrating the simplification process step by step.
- We examined methods to simplify radical expressions and the importance of perfect square factors.
- We highlighted practical uses of square roots in real-world scenarios, emphasizing their relevance in various scientific and mathematical contexts.
- We provided visual aids and comparisons with other square roots to reinforce understanding.
- Common misconceptions were clarified to prevent common errors in simplification.
By understanding and practicing these concepts, one can gain a deeper appreciation of the beauty and utility of mathematics. The square root of 18, while a specific example, serves as a gateway to broader mathematical understanding and application.
We encourage continued exploration and practice to master these concepts and apply them confidently in both academic and real-world settings.
Video hướng dẫn cách đơn giản hóa căn bậc hai của 18: Sqrt(18) giúp bạn hiểu rõ và áp dụng đúng phương pháp.
Cách Đơn Giản Hóa Căn Bậc Hai của 18: Sqrt(18)
READ MORE:
Video giải thích căn bậc hai của 18 và cách đơn giản hóa biểu thức này.
Căn Bậc Hai của 18