Topic polynomials area and perimeter: Discover the fascinating world of polynomials and their applications in calculating area and perimeter. This comprehensive guide simplifies complex concepts, making it easy for anyone to understand and apply polynomials in geometry. Enhance your mathematical skills and explore real-life examples that demonstrate the power of polynomials in solving geometric problems.
Table of Content
- Polynomials: Area and Perimeter
- Introduction to Polynomials
- Understanding Polynomials in Geometry
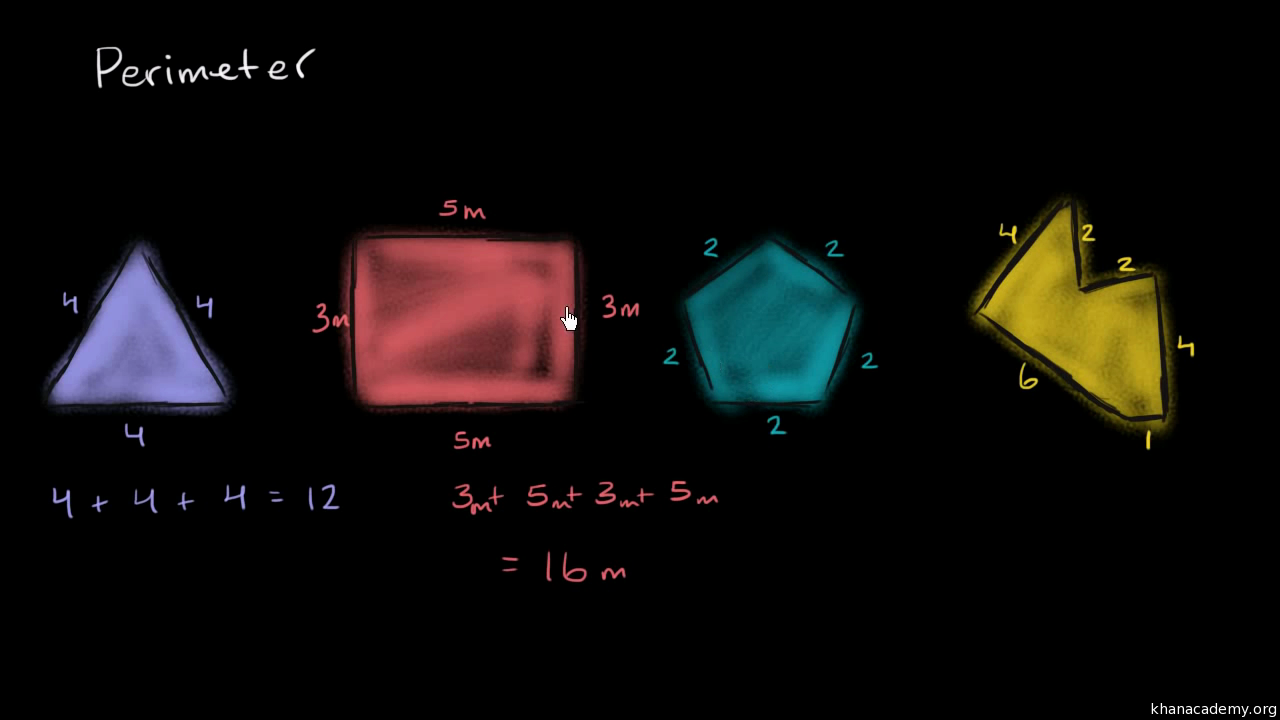
- Basic Concepts of Area and Perimeter
- Application of Polynomials in Calculating Area
- Application of Polynomials in Calculating Perimeter
- Formulas for Area Using Polynomials
- Formulas for Perimeter Using Polynomials
- Examples of Area Calculations with Polynomials
- Examples of Perimeter Calculations with Polynomials
- Practice Problems on Area with Polynomial Solutions
- Practice Problems on Perimeter with Polynomial Solutions
- Common Mistakes in Polynomial Area and Perimeter Calculations
- Advanced Topics in Polynomial Geometry
- Real-life Applications of Polynomials in Geometry
- Interactive Tools and Resources
- Conclusion and Further Reading
- YOUTUBE: Video này hướng dẫn cách sử dụng đa thức để tìm diện tích và chu vi, phù hợp cho học sinh và người học toán muốn nâng cao kiến thức.
Polynomials: Area and Perimeter
Understanding how to use polynomials to calculate area and perimeter is a valuable skill in mathematics. Below are detailed explanations and examples on how to approach these problems using polynomial expressions.
Area of Geometric Shapes Using Polynomials
- Rectangle: The area of a rectangle can be expressed as \( A = l \cdot w \). For a rectangle with sides \( y + 7 \) and \( y + 9 \), the polynomial for the area is: \[ A = (y + 7)(y + 9) = y^2 + 16y + 63 \]
- Triangle: The area of a triangle is given by \( A = \frac{1}{2} \cdot \text{base} \cdot \text{height} \). For a triangle with base \( x + 4 \) and height 3, the polynomial for the area is: \[ A = \frac{1}{2} (x + 4) \cdot 3 = \frac{3}{2}(x + 4)
- Complex Shapes: For a shape that combines multiple basic shapes, such as a square and a triangle, calculate the area of each part separately and then sum them. For example, a shape with a square of side \( x + 2 \) and a triangle with base \( x + 2 \) and height \( x \): \[ \text{Area of square} = (x + 2)^2 = x^2 + 4x + 4 \] \[ \text{Area of triangle} = \frac{1}{2} (x + 2) \cdot x = \frac{x(x + 2)}{2} \] \[ \text{Total Area} = x^2 + 4x + 4 + \frac{x(x + 2)}{2} \]
Perimeter of Geometric Shapes Using Polynomials
- Square: If each side of a square is \( 2x + 3 \), the perimeter \( P \) is: \[ P = 4(2x + 3) = 8x + 12
- Complex Shapes: For a complex shape with sides of different lengths, sum the polynomial expressions of each side. For example, for a shape with sides \( 2x - 1 \), \( 3x \), \( 5x \), and \( 4x - 2 \): \[ P = (2x - 1) + 3x + 5x + (4x - 2) = 14x - 3
Examples and Practice Problems
- If each side of a square is \( 3x - 4 \), what is the perimeter of the square?
- Answer: \( P = 4(3x - 4) = 12x - 16 \)
- Find the perimeter of a rectangle if the length is \( 3x^2 - 5 \) and the width is \( 3x + 3 \):
- Answer: \( P = 2((3x^2 - 5) + (3x + 3)) = 6x^2 + 6x - 4 \)
Practicing these types of problems will help reinforce your understanding of how to work with polynomials in geometric contexts. For more exercises and detailed explanations, refer to the sources listed below.

READ MORE:
Introduction to Polynomials
Polynomials are algebraic expressions that consist of variables and coefficients, combined using addition, subtraction, and multiplication operations. A polynomial can be represented in the general form:
\( P(x) = a_n x^n + a_{n-1} x^{n-1} + \ldots + a_1 x + a_0 \)
where:
- \( a_n, a_{n-1}, \ldots, a_1, a_0 \) are constants known as coefficients.
- \( x \) is the variable.
- \( n \) is a non-negative integer representing the degree of the polynomial.
Polynomials play a crucial role in various areas of mathematics, including geometry. They are used to describe curves, calculate areas, and determine perimeters of geometric shapes.
Here are some key properties of polynomials:
- Degree: The degree of a polynomial is the highest power of the variable in the expression. For example, the degree of \( 3x^4 + 2x^3 - x + 7 \) is 4.
- Coefficients: These are the numerical factors in each term of the polynomial. In \( 5x^2 + 3x - 1 \), the coefficients are 5, 3, and -1.
- Constant Term: This is the term without a variable. In \( 2x^3 - x^2 + 4x + 6 \), the constant term is 6.
Polynomials can be classified based on their degree:
| Degree | Name | Example |
| 0 | Constant | 5 |
| 1 | Linear | \( 2x + 3 \) |
| 2 | Quadratic | \( x^2 - 4x + 4 \) |
| 3 | Cubic | \( x^3 + x^2 - x + 1 \) |
Polynomials are fundamental in calculating areas and perimeters in geometry. By using polynomial equations, we can model and solve various geometric problems, making them an essential tool in mathematical analysis.
Understanding Polynomials in Geometry
Polynomials are widely used in geometry to describe and solve various problems related to shapes, areas, and perimeters. By representing geometric properties with polynomials, we can apply algebraic methods to find solutions efficiently.
Here are some fundamental ways in which polynomials are applied in geometry:
- Equation of a Line:
A linear polynomial represents the equation of a line. For example, the equation \( y = mx + c \) is a first-degree polynomial where \( m \) is the slope and \( c \) is the y-intercept.
- Equation of a Parabola:
A quadratic polynomial can represent the equation of a parabola. For instance, \( y = ax^2 + bx + c \) describes a parabolic curve where \( a \), \( b \), and \( c \) are constants.
- Area Calculation:
Polynomials can be used to express the area of various shapes. For example, the area \( A \) of a rectangle with length \( l \) and width \( w \) is given by the polynomial \( A = lw \).
For a triangle with base \( b \) and height \( h \), the area is \( A = \frac{1}{2}bh \).
- Perimeter Calculation:
The perimeter \( P \) of a geometric shape can also be represented by polynomials. For instance, the perimeter of a rectangle is \( P = 2l + 2w \).
For a triangle with sides \( a \), \( b \), and \( c \), the perimeter is \( P = a + b + c \).
To further illustrate the use of polynomials in geometry, consider the following examples:
| Shape | Area Polynomial | Perimeter Polynomial |
| Square | \( A = s^2 \) | \( P = 4s \) |
| Circle | \( A = \pi r^2 \) | \( P = 2\pi r \) |
| Trapezoid | \( A = \frac{1}{2}(b_1 + b_2)h \) | \( P = a + b_1 + b_2 + d \) |
By utilizing polynomials, complex geometric problems can be transformed into manageable algebraic equations. This approach not only simplifies the process of solving for areas and perimeters but also enhances our overall understanding of geometric relationships.
Basic Concepts of Area and Perimeter
Understanding the basic concepts of area and perimeter is fundamental in geometry. These concepts help in determining the size and boundaries of various shapes and objects. Here's a detailed overview of these concepts:
Area
The area of a shape is the measure of the space enclosed within its boundaries. It is expressed in square units, such as square meters (\( m^2 \)), square centimeters (\( cm^2 \)), etc. Different shapes have different formulas for calculating area:
- Rectangle: For a rectangle with length \( l \) and width \( w \), the area \( A \) is given by: \[ A = l \times w \]
- Square: For a square with side length \( s \), the area \( A \) is: \[ A = s^2 \]
- Triangle: For a triangle with base \( b \) and height \( h \), the area \( A \) is: \[ A = \frac{1}{2} \times b \times h \]
- Circle: For a circle with radius \( r \), the area \( A \) is: \[ A = \pi r^2 \]
Perimeter
The perimeter of a shape is the total length of its boundaries. It is expressed in linear units, such as meters (m), centimeters (cm), etc. Here are the perimeter formulas for various shapes:
- Rectangle: For a rectangle with length \( l \) and width \( w \), the perimeter \( P \) is: \[ P = 2l + 2w \]
- Square: For a square with side length \( s \), the perimeter \( P \) is: \[ P = 4s \]
- Triangle: For a triangle with sides \( a \), \( b \), and \( c \), the perimeter \( P \) is: \[ P = a + b + c \]
- Circle: For a circle with radius \( r \), the perimeter (circumference) \( P \) is: \[ P = 2\pi r \]
Here is a summary table of the area and perimeter formulas for quick reference:
| Shape | Area | Perimeter |
| Rectangle | \( A = l \times w \) | \( P = 2l + 2w \) |
| Square | \( A = s^2 \) | \( P = 4s \) |
| Triangle | \( A = \frac{1}{2} \times b \times h \) | \( P = a + b + c \) |
| Circle | \( A = \pi r^2 \) | \( P = 2\pi r \) |
By mastering these basic concepts and formulas, you can efficiently calculate the area and perimeter of various geometric shapes, laying a strong foundation for more advanced geometric and algebraic problems.
Application of Polynomials in Calculating Area
Polynomials are powerful tools for calculating the area of various geometric shapes. By representing dimensions as polynomial expressions, we can apply algebraic techniques to determine areas efficiently. Here’s a detailed look at how polynomials are used in area calculations:
Rectangles and Squares
For rectangles and squares, the area can be expressed using polynomial equations.
- Rectangle:
Consider a rectangle with length \( l \) and width \( w \). The area \( A \) is given by the polynomial:
\[ A = l \times w \]If \( l \) and \( w \) are polynomials, for example, \( l = 3x + 2 \) and \( w = x - 1 \), the area is:
\[ A = (3x + 2)(x - 1) = 3x^2 - 3x + 2x - 2 = 3x^2 - x - 2 \] - Square:
For a square with side length \( s \), the area \( A \) is:
\[ A = s^2 \]If \( s = 2x + 3 \), then:
\[ A = (2x + 3)^2 = 4x^2 + 12x + 9 \]
Triangles
For triangles, the area can also be expressed using polynomial equations.
- Triangle:
For a triangle with base \( b \) and height \( h \), the area \( A \) is given by:
\[ A = \frac{1}{2} \times b \times h \]If \( b = 4x + 1 \) and \( h = x + 2 \), the area is:
\[ A = \frac{1}{2} \times (4x + 1)(x + 2) = \frac{1}{2} \times (4x^2 + 8x + x + 2) = \frac{1}{2} \times (4x^2 + 9x + 2) = 2x^2 + 4.5x + 1 \]
Circles
Polynomials can approximate the area of circles using the radius.
- Circle:
For a circle with radius \( r \), the area \( A \) is:
\[ A = \pi r^2 \]If \( r = x + 1 \), then:
\[ A = \pi (x + 1)^2 = \pi (x^2 + 2x + 1) = \pi x^2 + 2\pi x + \pi \]
Composite Shapes
For composite shapes, polynomials can represent the total area by summing the areas of individual shapes.
- Example:
Consider a shape composed of a rectangle and a semicircle. If the rectangle has dimensions \( l = 3x \) and \( w = 2x \), and the semicircle has radius \( r = x \), the total area \( A \) is:
Area of rectangle:
\[ A_{\text{rect}} = l \times w = 3x \times 2x = 6x^2 \]Area of semicircle:
\[ A_{\text{semi}} = \frac{1}{2} \pi r^2 = \frac{1}{2} \pi x^2 \]Total area:
\[ A = A_{\text{rect}} + A_{\text{semi}} = 6x^2 + \frac{1}{2} \pi x^2 = 6x^2 + 0.5 \pi x^2 \]
By using polynomials, we can easily handle complex area calculations and apply algebraic methods to solve geometric problems effectively.

Application of Polynomials in Calculating Perimeter
Polynomials are valuable tools for calculating the perimeter of various geometric shapes. By expressing dimensions as polynomial expressions, we can use algebraic methods to determine perimeters efficiently. Here’s a detailed look at how polynomials are applied in perimeter calculations:
Rectangles and Squares
For rectangles and squares, the perimeter can be expressed using polynomial equations.
- Rectangle:
Consider a rectangle with length \( l \) and width \( w \). The perimeter \( P \) is given by the polynomial:
\[ P = 2l + 2w \]If \( l \) and \( w \) are polynomials, for example, \( l = 3x + 2 \) and \( w = x - 1 \), the perimeter is:
\[ P = 2(3x + 2) + 2(x - 1) = 6x + 4 + 2x - 2 = 8x + 2 \] - Square:
For a square with side length \( s \), the perimeter \( P \) is:
\[ P = 4s \]If \( s = 2x + 3 \), then:
\[ P = 4(2x + 3) = 8x + 12 \]
Triangles
For triangles, the perimeter can also be expressed using polynomial equations.
- Triangle:
For a triangle with sides \( a \), \( b \), and \( c \), the perimeter \( P \) is given by:
\[ P = a + b + c \]If \( a = x + 1 \), \( b = 2x - 3 \), and \( c = x + 4 \), the perimeter is:
\[ P = (x + 1) + (2x - 3) + (x + 4) = 4x + 2 \]
Circles
Polynomials can approximate the circumference (perimeter) of circles using the radius.
- Circle:
For a circle with radius \( r \), the circumference \( C \) is:
\[ C = 2\pi r \]If \( r = x + 1 \), then:
\[ C = 2\pi (x + 1) = 2\pi x + 2\pi \]
Composite Shapes
For composite shapes, polynomials can represent the total perimeter by summing the perimeters of individual shapes.
- Example:
Consider a shape composed of a rectangle and a semicircle. If the rectangle has dimensions \( l = 3x \) and \( w = 2x \), and the semicircle has radius \( r = x \), the total perimeter \( P \) is:
Perimeter of rectangle (excluding the side shared with the semicircle):
\[ P_{\text{rect}} = 2l + w = 2(3x) + 2x = 8x \]Perimeter of semicircle:
\[ P_{\text{semi}} = \pi r = \pi x \]Total perimeter:
\[ P = P_{\text{rect}} + P_{\text{semi}} = 8x + \pi x = (8 + \pi)x \]
By using polynomials, complex perimeter calculations can be simplified, allowing for more efficient problem-solving in geometric contexts.
Formulas for Area Using Polynomials
Polynomials provide a versatile method for calculating the area of various geometric shapes. By expressing the dimensions of shapes as polynomials, we can derive area formulas that facilitate efficient problem-solving. Below are detailed formulas for calculating the area of different shapes using polynomials:
Rectangles and Squares
- Rectangle:
For a rectangle with length \( l \) and width \( w \), the area \( A \) is:
\[ A = l \times w \]If \( l \) and \( w \) are polynomials, for example, \( l = 3x + 2 \) and \( w = x - 1 \), then:
\[ A = (3x + 2)(x - 1) = 3x^2 - 3x + 2x - 2 = 3x^2 - x - 2 \] - Square:
For a square with side length \( s \), the area \( A \) is:
\[ A = s^2 \]If \( s = 2x + 3 \), then:
\[ A = (2x + 3)^2 = 4x^2 + 12x + 9 \]
Triangles
- Triangle:
For a triangle with base \( b \) and height \( h \), the area \( A \) is:
\[ A = \frac{1}{2} \times b \times h \]If \( b = 4x + 1 \) and \( h = x + 2 \), then:
\[ A = \frac{1}{2} \times (4x + 1)(x + 2) = \frac{1}{2} \times (4x^2 + 8x + x + 2) = \frac{1}{2} \times (4x^2 + 9x + 2) = 2x^2 + 4.5x + 1 \]
Circles
- Circle:
For a circle with radius \( r \), the area \( A \) is:
\[ A = \pi r^2 \]If \( r = x + 1 \), then:
\[ A = \pi (x + 1)^2 = \pi (x^2 + 2x + 1) = \pi x^2 + 2\pi x + \pi \]
Trapezoids
- Trapezoid:
For a trapezoid with bases \( b_1 \) and \( b_2 \) and height \( h \), the area \( A \) is:
\[ A = \frac{1}{2} (b_1 + b_2) h \]If \( b_1 = 3x + 1 \), \( b_2 = x + 2 \), and \( h = 2x \), then:
\[ A = \frac{1}{2} (3x + 1 + x + 2) 2x = \frac{1}{2} (4x + 3) 2x = (4x + 3) x = 4x^2 + 3x \]
Composite Shapes
- Composite Shape:
For a composite shape, the area is the sum of the areas of its individual components. Consider a shape composed of a rectangle and a semicircle. If the rectangle has dimensions \( l = 3x \) and \( w = 2x \), and the semicircle has radius \( r = x \), the total area \( A \) is:
Area of rectangle:
\[ A_{\text{rect}} = l \times w = 3x \times 2x = 6x^2 \]Area of semicircle:
\[ A_{\text{semi}} = \frac{1}{2} \pi r^2 = \frac{1}{2} \pi x^2 \]Total area:
\[ A = A_{\text{rect}} + A_{\text{semi}} = 6x^2 + \frac{1}{2} \pi x^2 = 6x^2 + 0.5 \pi x^2 \]
Using these polynomial formulas for calculating areas simplifies the process and makes solving complex geometric problems more manageable.
Formulas for Perimeter Using Polynomials
Polynomials are effective for calculating the perimeter of various geometric shapes. By expressing dimensions as polynomial equations, we can simplify the process and achieve accurate results. Below are detailed formulas for calculating the perimeter of different shapes using polynomials:
Rectangles and Squares
- Rectangle:
For a rectangle with length \( l \) and width \( w \), the perimeter \( P \) is:
\[ P = 2l + 2w \]If \( l \) and \( w \) are polynomials, for example, \( l = 3x + 2 \) and \( w = x - 1 \), then:
\[ P = 2(3x + 2) + 2(x - 1) = 6x + 4 + 2x - 2 = 8x + 2 \] - Square:
For a square with side length \( s \), the perimeter \( P \) is:
\[ P = 4s \]If \( s = 2x + 3 \), then:
\[ P = 4(2x + 3) = 8x + 12 \]
Triangles
- Triangle:
For a triangle with sides \( a \), \( b \), and \( c \), the perimeter \( P \) is:
\[ P = a + b + c \]If \( a = x + 1 \), \( b = 2x - 3 \), and \( c = x + 4 \), then:
\[ P = (x + 1) + (2x - 3) + (x + 4) = 4x + 2 \]
Circles
- Circle:
For a circle with radius \( r \), the circumference \( C \) is:
\[ C = 2\pi r \]If \( r = x + 1 \), then:
\[ C = 2\pi (x + 1) = 2\pi x + 2\pi \]
Polygons
- Regular Polygon:
For a regular polygon with \( n \) sides, each of length \( s \), the perimeter \( P \) is:
\[ P = n \times s \]If \( s = 3x + 2 \) and \( n = 6 \), then:
\[ P = 6 \times (3x + 2) = 18x + 12 \]
Composite Shapes
- Composite Shape:
For a composite shape, the perimeter is the sum of the perimeters of its individual components. Consider a shape composed of a rectangle and a semicircle. If the rectangle has dimensions \( l = 3x \) and \( w = 2x \), and the semicircle has radius \( r = x \), the total perimeter \( P \) is:
Perimeter of rectangle (excluding the side shared with the semicircle):
\[ P_{\text{rect}} = 2l + w = 2(3x) + 2x = 8x \]Perimeter of semicircle:
\[ P_{\text{semi}} = \pi r = \pi x \]Total perimeter:
\[ P = P_{\text{rect}} + P_{\text{semi}} = 8x + \pi x = (8 + \pi)x \]
Using these polynomial formulas for calculating perimeters simplifies the process and makes solving complex geometric problems more manageable.
Examples of Area Calculations with Polynomials
Calculating the area of geometric shapes using polynomials can simplify and enhance understanding. Here are some detailed examples illustrating how to use polynomial expressions for area calculations:
Example 1: Area of a Rectangle
Consider a rectangle with length \( l = 3x + 2 \) and width \( w = x - 1 \). To find the area \( A \), we use the formula:
- Step 1: Write the area formula for a rectangle: \[ A = l \times w \]
- Step 2: Substitute the polynomial expressions for \( l \) and \( w \): \[ A = (3x + 2)(x - 1) \]
- Step 3: Expand the polynomial: \[ A = 3x(x) + 3x(-1) + 2(x) + 2(-1) \] \[ A = 3x^2 - 3x + 2x - 2 \] \[ A = 3x^2 - x - 2 \]
Example 2: Area of a Square
Consider a square with side length \( s = 2x + 3 \). To find the area \( A \), we use the formula:
- Step 1: Write the area formula for a square: \[ A = s^2 \]
- Step 2: Substitute the polynomial expression for \( s \): \[ A = (2x + 3)^2 \]
- Step 3: Expand the polynomial: \[ A = (2x + 3)(2x + 3) \] \[ A = 2x(2x) + 2x(3) + 3(2x) + 3(3) \] \[ A = 4x^2 + 6x + 6x + 9 \] \[ A = 4x^2 + 12x + 9 \]
Example 3: Area of a Triangle
Consider a triangle with base \( b = 4x + 1 \) and height \( h = x + 2 \). To find the area \( A \), we use the formula:
- Step 1: Write the area formula for a triangle: \[ A = \frac{1}{2} \times b \times h \]
- Step 2: Substitute the polynomial expressions for \( b \) and \( h \): \[ A = \frac{1}{2} \times (4x + 1)(x + 2) \]
- Step 3: Expand the polynomial: \[ A = \frac{1}{2} \times (4x(x) + 4x(2) + 1(x) + 1(2)) \] \[ A = \frac{1}{2} \times (4x^2 + 8x + x + 2) \] \[ A = \frac{1}{2} \times (4x^2 + 9x + 2) \] \[ A = 2x^2 + 4.5x + 1 \]
Example 4: Area of a Circle
Consider a circle with radius \( r = x + 1 \). To find the area \( A \), we use the formula:
- Step 1: Write the area formula for a circle: \[ A = \pi r^2 \]
- Step 2: Substitute the polynomial expression for \( r \): \[ A = \pi (x + 1)^2 \]
- Step 3: Expand the polynomial: \[ A = \pi (x + 1)(x + 1) \] \[ A = \pi (x(x) + x(1) + 1(x) + 1(1)) \] \[ A = \pi (x^2 + x + x + 1) \] \[ A = \pi (x^2 + 2x + 1) \] \[ A = \pi x^2 + 2\pi x + \pi \]
These examples demonstrate how polynomial expressions can be used to simplify the calculation of areas for various geometric shapes. By understanding and applying these methods, complex area calculations become more manageable and intuitive.

Examples of Perimeter Calculations with Polynomials
Let's delve into some practical examples of how polynomials are used to calculate perimeters in various geometric shapes:
- Rectangle: Consider a rectangle with sides represented by polynomials. Let the length of the rectangle be \( L(x) = 3x + 2 \) and the width be \( W(x) = 2x + 5 \). The perimeter \( P \) of the rectangle can be calculated using the formula: \( P = 2L + 2W \). Substituting the given polynomial expressions, we get: \[ P = 2(3x + 2) + 2(2x + 5) \] \[ P = 6x + 4 + 4x + 10 \] \[ P = 10x + 14 \]
- Triangle: Let's consider an equilateral triangle where all three sides are represented by the polynomial \( S(x) = 4x^2 + 3x + 1 \). The perimeter \( P \) of the equilateral triangle can be found by multiplying the side length by 3, i.e., \( P = 3S \). Substituting the polynomial expression, we get: \[ P = 3(4x^2 + 3x + 1) \] \[ P = 12x^2 + 9x + 3 \]
- Circle: Consider a circle with radius represented by the polynomial \( R(x) = 2x^2 + 5x + 3 \). The perimeter \( P \) of the circle, also known as the circumference, can be calculated using the formula \( P = 2\pi R \), where \( \pi \) is the mathematical constant pi. Substituting the given polynomial expression, we get: \[ P = 2\pi(2x^2 + 5x + 3) \] \[ P = 4\pi x^2 + 10\pi x + 6\pi \]
These examples illustrate how polynomials can be employed to compute perimeters in different geometric contexts, showcasing their versatility and applicability.
Practice Problems on Area with Polynomial Solutions
Let's tackle some practice problems involving the calculation of areas using polynomial solutions:
- Quadrilateral Area: Given a quadrilateral with side lengths represented by polynomials, such as \( L(x) = 3x^2 + 2x + 1 \), \( W(x) = 2x + 5 \), \( H(x) = 4x^3 + 2x^2 + 3x + 1 \), and \( B(x) = 5x^2 + 3x + 2 \), find the area \( A \). The area of a quadrilateral can be calculated using various methods, including splitting it into triangles or using more complex formulas specific to the shape.
- Circle Sector Area: Consider a circle with radius \( R(x) = x^2 + 3x + 2 \). Find the area \( A \) of a sector with a central angle \( \theta \) represented by the polynomial \( \theta(x) = 2x^2 + 5x + 1 \). The area of a sector of a circle can be calculated using the formula \( A = \frac{1}{2} R^2 \theta \).
- Polygon Area: Given a regular polygon with side length represented by the polynomial \( S(x) = 4x + 3 \) and number of sides \( n(x) = 2x + 1 \), find the area \( A \). The area of a regular polygon can be calculated using the formula \( A = \frac{1}{4} nS^2 \cot\left(\frac{\pi}{n}\right) \).
These practice problems offer a chance to apply polynomial solutions to real-world geometric scenarios, enhancing your understanding and problem-solving skills.
Practice Problems on Perimeter with Polynomial Solutions
Let's engage in some practice problems involving the calculation of perimeters using polynomial solutions:
- Trapezoid Perimeter: Consider a trapezoid with bases represented by polynomials, such as \( B_1(x) = 3x + 2 \) and \( B_2(x) = 2x + 5 \), and height \( H(x) = 4x^2 + 3x + 1 \). Find the perimeter \( P \). The perimeter of a trapezoid can be calculated by adding the lengths of all four sides together.
- Regular Polygon Perimeter: Given a regular polygon with side length represented by the polynomial \( S(x) = 4x^2 + 2x + 3 \) and number of sides \( n(x) = 3x + 1 \), find the perimeter \( P \). The perimeter of a regular polygon is simply the product of the number of sides and the length of each side.
- Composite Shape Perimeter: Consider a composite shape made up of multiple polygons, each represented by polynomials for their side lengths. Calculate the perimeter \( P \) of the composite shape by summing the perimeters of each individual polygon.
These practice problems provide an opportunity to utilize polynomial solutions in solving perimeter-related challenges, fostering a deeper understanding of geometric concepts.
Common Mistakes in Polynomial Area and Perimeter Calculations
While working with polynomials in area and perimeter calculations, it's essential to be mindful of common mistakes that can occur:
- Incorrect Polynomial Operations: One common mistake is misapplying polynomial operations, such as addition, subtraction, multiplication, or division, when calculating areas or perimeters. Ensure that polynomial terms are properly combined and simplified.
- Using Incorrect Formulas: Another mistake is using incorrect formulas for specific geometric shapes. Different shapes require different formulas for calculating areas and perimeters. Always verify the appropriate formula for the given shape.
- Omitting Units: Forgetting to include units in the final answer is a common oversight. Always remember to include the correct units (e.g., square units for area, linear units for perimeter) in the final result.
- Ignoring Precision: Neglecting to round or approximate final answers to the appropriate level of precision can lead to inaccuracies in calculations. Be sure to adhere to the required level of precision specified in the problem.
- Skipping Intermediate Steps: Rushing through calculations without showing intermediate steps can make it challenging to identify errors. Take the time to show each step of the calculation process, making it easier to trace and correct mistakes.
By being aware of these common pitfalls and practicing careful attention to detail, you can minimize errors and improve the accuracy of polynomial area and perimeter calculations.
Advanced Topics in Polynomial Geometry
Exploring polynomial geometry unveils several advanced topics that delve deeper into the intricate relationship between polynomials and geometric shapes:
- Bezier Curves: Bezier curves are widely used in computer graphics and design. These curves are defined by polynomial equations and offer precise control over the shape of curves, making them essential in modeling complex shapes and surfaces.
- B-spline Curves and Surfaces: B-spline curves and surfaces are another fundamental concept in polynomial geometry. These curves and surfaces are defined by polynomial equations and provide a flexible framework for representing smooth, continuous shapes in computer-aided design (CAD) and computer-aided manufacturing (CAM).
- Algebraic Geometry: Algebraic geometry explores the relationship between geometric shapes and algebraic equations, including polynomials. This field investigates the properties of geometric objects defined by polynomial equations and has applications in diverse areas such as cryptography, robotics, and optimization.
- Rational Curves and Surfaces: Rational curves and surfaces are defined by rational polynomial equations, where the coefficients are ratios of polynomials. These curves and surfaces offer additional flexibility in shape representation and are extensively used in CAD, animation, and industrial design.
- Implicitization and Parametrization: Implicitization and parametrization are techniques used to convert geometric shapes defined by implicit equations (e.g., polynomial equations) into parametric form and vice versa. These techniques play a crucial role in solving geometric problems and analyzing geometric structures.
By delving into these advanced topics, one can gain a deeper understanding of the intricate connections between polynomials and geometric concepts, paving the way for innovative applications and problem-solving approaches.
Real-life Applications of Polynomials in Geometry
Polynomials play a significant role in various real-life applications, especially in geometry. They are used to describe and solve problems related to areas, perimeters, and volumes of geometric shapes. Here are some detailed applications:
-
Area and Perimeter of Land Parcels:
Polynomials are used in land surveying to calculate the area and perimeter of irregular land parcels. For instance, the area of a plot can be divided into several sections, each represented by a polynomial. Summing these polynomials gives the total area.
-
Architecture and Construction:
In architecture, polynomials help in designing and modeling buildings. The area and volume calculations of various components, like rooms and beams, are often polynomial functions. This aids architects in creating accurate blueprints and models.
-
Engineering and Manufacturing:
Polynomials are used to optimize material usage. For example, the perimeter and area formulas involving polynomials help in determining the most efficient way to cut materials with minimal waste, such as metal sheets or wood.
-
Physics and Astronomy:
Polynomials describe the trajectories of objects. In physics, the height of a projectile over time can be represented by a polynomial equation. Similarly, in astronomy, the orbits of planets and satellites are modeled using polynomial equations.
-
Economics:
Cost, revenue, and profit in economics can be modeled using polynomials. For instance, the cost function might be a linear polynomial, while the revenue function could be a quadratic polynomial, helping businesses to find the break-even points and maximize profits.
Let's explore a specific example involving the volume of a cylinder:
Consider a cylinder with height \( h = 7 \) and radius \( r = t - 2 \). The volume \( V \) of the cylinder can be calculated using the polynomial formula:
V = \pi r^2 h
= \pi (t-2)^2 \cdot 7
= 7\pi (t^2 - 4t + 4)
= 7\pi t^2 - 28\pi t + 28\pi
This polynomial expression helps in determining the volume based on the variable \( t \), which might represent time or another changing factor.
Through these applications, it is evident that polynomials are indispensable tools in solving practical problems in geometry and beyond.
Interactive Tools and Resources
Understanding polynomials and their applications in calculating area and perimeter can be greatly enhanced using interactive tools and resources. Here are some valuable tools and platforms to help you explore these concepts:
-
PhET Interactive Simulations: This platform offers a variety of interactive simulations, including the Area Model Algebra tool. It allows students to build rectangles of various sizes, relate multiplication to area, and discover strategies for multiplying algebraic expressions. Explore the tool at .
-
Desmos Graphing Calculator: Desmos provides a powerful online graphing calculator that can visualize polynomial functions, plot points, and more. This tool helps students understand the graphical representation of polynomial equations, making it easier to grasp their behavior and properties. Try it out at .
-
Toy Theater's Area Perimeter Explorer: This interactive game allows students to create shapes using colored blocks on a grid and instantly see the perimeter and area calculations. It's an excellent way for students to practice and reinforce their understanding of these concepts. Access the game at .
-
Khan Academy: Khan Academy offers comprehensive lessons on polynomial expressions, equations, and functions, including applications in geometry. Their interactive exercises and instructional videos provide a thorough understanding of the topics. Visit .
These resources offer interactive and engaging ways to learn and apply polynomial concepts in calculating area and perimeter, making the learning process both effective and enjoyable.
Conclusion and Further Reading
Polynomials are a fundamental component in various fields of mathematics, especially in geometry where they are used to calculate areas and perimeters of complex shapes. Their applications extend beyond simple academic exercises to real-life scenarios, including architecture, engineering, and computer graphics.
Understanding the principles of polynomial equations and their geometric applications can significantly enhance problem-solving skills. This knowledge is not only useful for theoretical mathematics but also for practical applications such as designing efficient structures, optimizing resources, and solving real-world problems with precision.
To delve deeper into the subject, here are some recommended resources for further reading:
- - This resource provides detailed explanations and examples of polynomial applications in various contexts.
- - A comprehensive series of lessons and practice problems to enhance your understanding of polynomials in algebra and geometry.
- - A collection of practice problems to apply your knowledge of polynomials in calculating areas and perimeters.
- - Video tutorials that offer visual explanations on how to find the area of shapes using polynomials.
By exploring these resources, you can gain a deeper understanding and appreciation of the role polynomials play in both theoretical and applied mathematics. Keep practicing and exploring new problems to enhance your skills further.

Video này hướng dẫn cách sử dụng đa thức để tìm diện tích và chu vi, phù hợp cho học sinh và người học toán muốn nâng cao kiến thức.
Sử dụng đa thức để tìm diện tích và chu vi
READ MORE:
Video này hướng dẫn cách sử dụng đa thức để tính toán chu vi và diện tích, giúp học sinh và người học toán hiểu rõ hơn về các ứng dụng của đa thức trong hình học.
Chu vi và diện tích bằng cách sử dụng đa thức