What is the Perimeter of a Right Triangle: Simple Guide

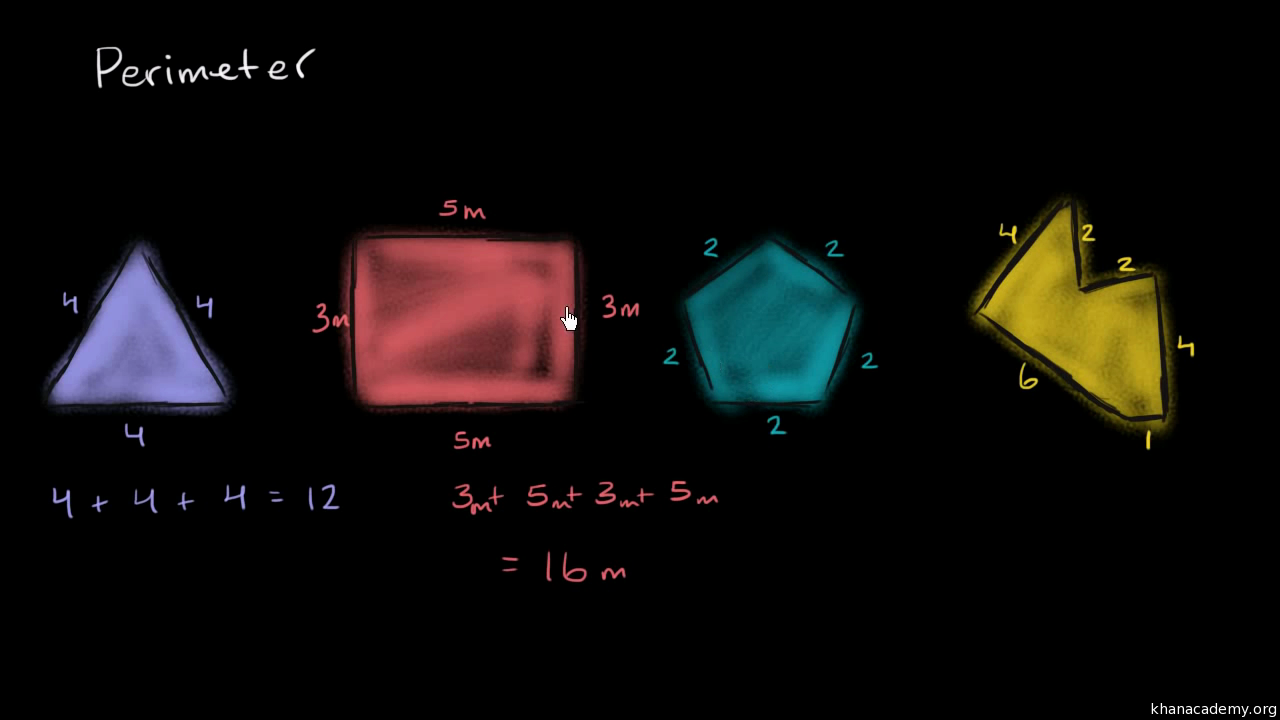
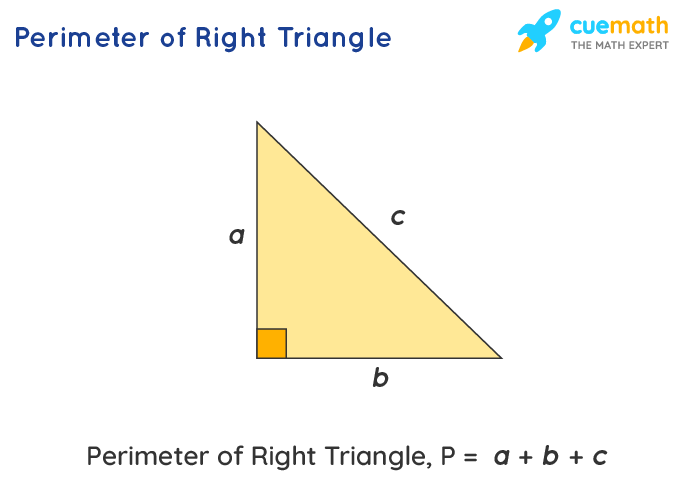
The perimeter of a right triangle is the total length around the triangle, which can be found by summing the lengths of all three sides.

Formula for the Perimeter

If the sides of a right triangle are denoted as a, b, and c (with c being the hypotenuse), the perimeter P is given by:

\[ P = a + b + c \]

Using the Pythagorean Theorem

If only the base b and the height a are known, the hypotenuse c can be found using the Pythagorean theorem:

\[ c = \sqrt{a^2 + b^2} \]

Then, the perimeter can be calculated as:

\[ P = a + b + \sqrt{a^2 + b^2} \]

Example Calculations

• Example 1: For a right triangle with base \( b = 6 \) units and height \( a = 8 \) units:
  1. Calculate the hypotenuse: \( c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = 10 \) units
  2. Calculate the perimeter: \( P = 6 + 8 + 10 = 24 \) units
• Example 2: For a right triangle with base \( b = 5 \) units and hypotenuse \( c = 13 \) units:
  1. Calculate the height using the Pythagorean theorem: \( a = \sqrt{c^2 - b^2} = \sqrt{13^2 - 5^2} = \sqrt{169 - 25} = 12 \) units
  2. Calculate the perimeter: \( P = 5 + 12 + 13 = 30 \) units

Special Right Triangles

Special right triangles have simple relationships between their side lengths:

• 30°-60°-90° triangle: The sides are in the ratio 1:√3:2
• 45°-45°-90° triangle: The sides are in the ratio 1:1:√2

For these triangles, knowing one side length allows easy calculation of the perimeter.

Applications

The perimeter of a right triangle is useful in various applications, such as determining the length of fencing needed to enclose a triangular area or in construction and design to ensure accurate measurements.

A right triangle, also known as a right-angled triangle, is a type of triangle that has one angle equal to 90 degrees. This unique property makes right triangles fundamental in various fields such as geometry, trigonometry, and even in real-life applications like construction and engineering. The sides of a right triangle have specific names: the side opposite the right angle is called the hypotenuse, and the other two sides are referred to as the legs.

The key characteristics of a right triangle include:

• Right Angle: One of the angles is exactly 90 degrees.
• Hypotenuse: The longest side, opposite the right angle.
• Legs: The two shorter sides that form the right angle.

The Pythagorean theorem is a fundamental principle related to right triangles. It states that in a right triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the lengths of the other two sides (a and b):

c^2 = a^2 + b^2

Using this theorem, if you know the lengths of any two sides of a right triangle, you can calculate the length of the third side. This principle is extremely useful for solving problems involving right triangles.

The perimeter of a right triangle is the sum of the lengths of all its sides. If the sides are denoted as a, b, and c, where c is the hypotenuse, the perimeter (P) can be calculated using the formula:

P = a + b + c

Understanding these basic properties and formulas of right triangles lays the foundation for exploring more advanced geometric concepts and applications.

The perimeter of a right triangle is the total length around its edges. In a right triangle, this includes the lengths of the two legs and the hypotenuse. The formula to calculate the perimeter (P) of a right triangle is:

\[ P = a + b + c \]

where \(a\) and \(b\) are the lengths of the legs, and \(c\) is the length of the hypotenuse.

Here are the steps to calculate the perimeter of a right triangle:

• Identify the lengths of the two legs, \(a\) and \(b\).
• If the length of the hypotenuse \(c\) is not known, use the Pythagorean Theorem to find it:

\[ c = \sqrt{a^2 + b^2} \]

• Once all three sides are known, simply add them together to find the perimeter:

\[ P = a + b + c \]

For example, if a right triangle has legs of lengths 6 units and 8 units, and the hypotenuse is 10 units, the perimeter is calculated as:

\[ P = 6 + 8 + 10 = 24 \text{ units} \]

In another example, if only the legs are known (e.g., 3 units and 4 units), first find the hypotenuse using the Pythagorean Theorem:

\[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{ units} \]

Then, calculate the perimeter:

\[ P = 3 + 4 + 5 = 12 \text{ units} \]

Thus, the perimeter of the triangle is 12 units. Understanding and applying these steps will help you easily calculate the perimeter of any right triangle.

The perimeter of a right triangle is the total distance around the triangle. It is calculated by adding the lengths of all three sides: the two legs and the hypotenuse. Given a right triangle with legs of lengths \(a\) and \(b\), and hypotenuse \(c\), the perimeter \(P\) can be determined using the formula:

$$P = a + b + c$$

Here are the steps to calculate the perimeter:

1. Identify the lengths of the legs \(a\) and \(b\).
2. Use the Pythagorean theorem to find the length of the hypotenuse \(c\): $$c = \sqrt{a^2 + b^2}$$
3. Sum the lengths of all three sides: $$P = a + b + c$$

Let's see an example:

• If the lengths of the legs are 3 units and 4 units:
  1. Calculate the hypotenuse: $$c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5$$
  2. Determine the perimeter: $$P = 3 + 4 + 5 = 12$$

Therefore, the perimeter of the right triangle with legs 3 units and 4 units is 12 units.

This formula and method ensure you can find the perimeter of any right triangle as long as you know the lengths of its sides.

In a right triangle, the hypotenuse is the longest side, opposite the right angle. To calculate the hypotenuse, you can use the Pythagorean Theorem, which states that the square of the hypotenuse (c) is equal to the sum of the squares of the other two sides (a and b).

1. Start with the Pythagorean Theorem:

   \( c^2 = a^2 + b^2 \)

2. Substitute the known values of the two shorter sides into the equation.
3. Solve for \( c^2 \) by adding the squares of the other two sides.
4. Take the square root of both sides to find the length of the hypotenuse:

   \( c = \sqrt{a^2 + b^2} \)

For example, if the lengths of the other two sides are 3 units and 4 units, you would calculate the hypotenuse as follows:

• Square the lengths of the two shorter sides:

  \( 3^2 = 9 \)

  \( 4^2 = 16 \)

• Add these squares together:

  \( 9 + 16 = 25 \)

• Take the square root of the result to find the hypotenuse:

  \( c = \sqrt{25} = 5 \)

Therefore, the hypotenuse of a right triangle with sides of 3 units and 4 units is 5 units.

Understanding the step-by-step process for calculating the perimeter of a right triangle can greatly simplify the problem-solving process. Below are detailed examples to help you grasp these calculations:

1. Example 1: Given a right triangle with side lengths of 3 units and 4 units, find the perimeter.

   • Step 1: Identify the lengths of the two legs. Here, a = 3 and b = 4.
   • Step 2: Calculate the hypotenuse using the Pythagorean theorem: \(c = \sqrt{a^2 + b^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\)
   • Step 3: Sum the lengths of all three sides to find the perimeter: \( \text{Perimeter} = a + b + c = 3 + 4 + 5 = 12 \, \text{units} \)

2. Example 2: Given a right triangle with a base of 5 units and a hypotenuse of 13 units, find the perimeter.

   • Step 1: Identify the base and hypotenuse. Here, base = 5 and hypotenuse = 13.
   • Step 2: Calculate the height using the Pythagorean theorem: \(c^2 = a^2 + b^2\) where \(c = 13\) and \(a = 5\) \\ \( 13^2 = 5^2 + b^2 \) \\ \( 169 = 25 + b^2 \) \\ \( b^2 = 144 \) \\ \( b = \sqrt{144} = 12 \)
   • Step 3: Sum the lengths of all three sides to find the perimeter: \( \text{Perimeter} = 5 + 12 + 13 = 30 \, \text{units} \)

A 30°-60°-90° triangle is a special right triangle with angles measuring 30°, 60°, and 90° respectively.

This type of triangle has unique properties in terms of its side lengths, which can be calculated using specific ratios.

The side lengths of a 30°-60°-90° triangle have a ratio of 1:√3:2.

Here's how the side lengths can be calculated:

• The side opposite the 30° angle (the shorter leg) is represented by \(a\).
• The side opposite the 60° angle (the longer leg) is \(a√3\).
• The hypotenuse (opposite the 90° angle) is \(2a\).

These relationships between the angles and side lengths allow for easier calculation of perimeter, area, and other properties of the triangle.

A 45°-45°-90° triangle, also known as an isosceles right triangle, is a special right triangle with two angles measuring 45° each and one right angle measuring 90°.

This type of triangle has distinct properties in terms of its side lengths, which can be calculated using specific ratios.

The side lengths of a 45°-45°-90° triangle have a ratio of 1:1:√2.

Here's how the side lengths can be determined:

• Both legs of the triangle are equal in length and are represented by \(a\).
• The length of the hypotenuse, opposite the right angle, is \(a√2\).

Understanding these relationships between the angles and side lengths enables easier calculation of the perimeter, area, and other properties of the triangle.

The concept of perimeter is not only a fundamental aspect of geometry but also finds numerous applications in real-life scenarios. Some of the key applications include:

1. Fencing: Perimeter is crucial in determining the amount of fencing needed for enclosing a garden, property, or any other area. By calculating the perimeter, one can accurately estimate the length of fencing material required.
2. Construction: In construction projects, understanding perimeter helps in determining the amount of material needed for laying foundations, installing borders, or constructing walls. It also aids in planning the layout of structures within a given area.
3. Landscaping: Perimeter calculations are essential for landscaping tasks such as laying pathways, installing retaining walls, or creating outdoor living spaces. It ensures proper utilization of space and efficient allocation of resources.
4. Parcel Measurement: Real estate professionals often use perimeter measurements to assess the size and boundaries of parcels of land. This information is crucial for property valuation, land development, and legal documentation.
5. Sports Fields: Perimeter is significant in designing and marking out sports fields such as soccer pitches, basketball courts, and tennis courts. It helps in ensuring that the dimensions meet regulatory standards and provide adequate playing space.
6. Security: Perimeter security systems rely on accurate perimeter measurements to determine the coverage area of surveillance cameras, motion sensors, and fencing installations. It plays a vital role in enhancing the safety and security of residential and commercial properties.

Overall, the practical applications of perimeter extend across various fields, demonstrating its importance in everyday life and professional endeavors.

When dealing with the perimeter of a right triangle, there are several common mistakes that learners should be mindful of to ensure accuracy and precision:

1. Forgetting to Include All Sides: One of the most common mistakes is forgetting to include all three sides of the right triangle when calculating the perimeter. It's essential to account for the lengths of the two legs and the hypotenuse.
2. Misidentifying the Hypotenuse: Confusion may arise in identifying the hypotenuse, especially in complex diagrams or non-standard orientations. It's crucial to correctly recognize the side opposite the right angle as the hypotenuse.
3. Incorrect Application of the Pythagorean Theorem: While the Pythagorean Theorem is a fundamental tool for calculating side lengths in right triangles, misapplication or misunderstanding of the theorem can lead to incorrect perimeter calculations.
4. Using Incorrect Formulas: Using incorrect formulas or ratios for special right triangles, such as the 30°-60°-90° or 45°-45°-90° triangles, can result in inaccurate perimeter calculations. It's important to understand the specific relationships between angles and side lengths.
5. Ignoring Units: Neglecting to include units (such as inches, centimeters, etc.) in perimeter calculations can lead to ambiguity or incorrect interpretations of the results. Always ensure consistency in units throughout the calculation.
6. Skipping Steps: Rushing through calculations without carefully following each step can increase the likelihood of errors. Taking the time to methodically work through the problem can help avoid mistakes.

By being aware of these common pitfalls and taking proactive measures to avoid them, learners can enhance their understanding of perimeter calculations in right triangles and improve accuracy in mathematical problem-solving.

Practice problems are an excellent way to reinforce understanding and mastery of perimeter calculations in right triangles. Below are some practice problems along with their solutions:

1. Problem 1: Calculate the perimeter of a right triangle with legs measuring 5 cm and 12 cm.

Solution: Using the Pythagorean Theorem, the length of the hypotenuse can be calculated as follows:

Leg 1:	\(a = 5\) cm
Leg 2:	\(b = 12\) cm
Hypotenuse:	\(c = \sqrt{a^2 + b^2} = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13\) cm

Therefore, the perimeter is \(5 + 12 + 13 = 30\) cm.

2. Problem 2: Find the perimeter of a right triangle with a hypotenuse measuring 10 units and one leg measuring 6 units.

Solution: Given the length of one leg and the hypotenuse, the length of the other leg can be found using the Pythagorean Theorem:

Hypotenuse:	\(c = 10\) units
Leg 1:	\(a = 6\) units
Leg 2:	\(b = \sqrt{c^2 - a^2} = \sqrt{10^2 - 6^2} = \sqrt{100 - 36} = \sqrt{64} = 8\) units

Therefore, the perimeter is \(6 + 8 + 10 = 24\) units.

Practicing these problems will help solidify concepts and improve problem-solving skills related to right triangle perimeters.

Here are some frequently asked questions about right triangle perimeters:

1. What is the perimeter of a right triangle?

The perimeter of a right triangle is the sum of the lengths of all three sides. It can be calculated using the formula: \( \text{Perimeter} = \text{Side 1} + \text{Side 2} + \text{Hypotenuse} \).

2. How do you find the perimeter of a right triangle if you know the lengths of its sides?

If you know the lengths of the two legs and the hypotenuse of a right triangle, you can simply add these lengths together to find the perimeter.

3. Can you find the perimeter of a right triangle if you only know the length of one side?

No, you cannot find the perimeter of a right triangle if you only know the length of one side. You need to know the lengths of at least two sides to calculate the perimeter.

4. What are some common methods for finding the perimeter of a right triangle?

Common methods for finding the perimeter of a right triangle include using the Pythagorean Theorem to find missing side lengths, applying trigonometric ratios in special right triangles, or directly adding the lengths of known sides.

5. Why is the perimeter of a right triangle important?

The perimeter of a right triangle is important because it provides information about the total length of its boundary. Understanding the perimeter is essential in various practical applications, such as construction, fencing, and land measurement.

These FAQs aim to address common inquiries about right triangle perimeters and provide clarity on related concepts.