Topic pythagorean theorem find the perimeter calculator: Unlock the power of the Pythagorean Theorem to effortlessly find the perimeter of right triangles. Our comprehensive guide and calculator make it easy to solve for any side or perimeter, whether you're a student, teacher, or enthusiast. Discover formulas, step-by-step instructions, and practical examples to enhance your mathematical skills.
Table of Content
- Pythagorean Theorem and Perimeter Calculator
- Introduction
- Understanding the Pythagorean Theorem
- Basic Formula
- Calculating the Hypotenuse
- Calculating the Other Sides
- Perimeter Calculation
- Examples and Applications
- Proof of the Pythagorean Theorem
- Using the Calculator
- Related Calculations
- Common Problems and Solutions
- Advanced Applications
- Frequently Asked Questions
- Resources and Further Reading
- YOUTUBE: Video hướng dẫn cách sử dụng Định lý Pythagoras để tính chu vi của các hình tam giác.
Pythagorean Theorem and Perimeter Calculator
The Pythagorean Theorem describes the relationship between the sides of a right triangle:
Calculate the Hypotenuse
Given the lengths of the two legs of a right triangle, you can find the hypotenuse:
Calculate the Length of a Side
Given the hypotenuse and one leg, you can find the other leg:
Calculate the Area
The area of a right triangle can be calculated as:
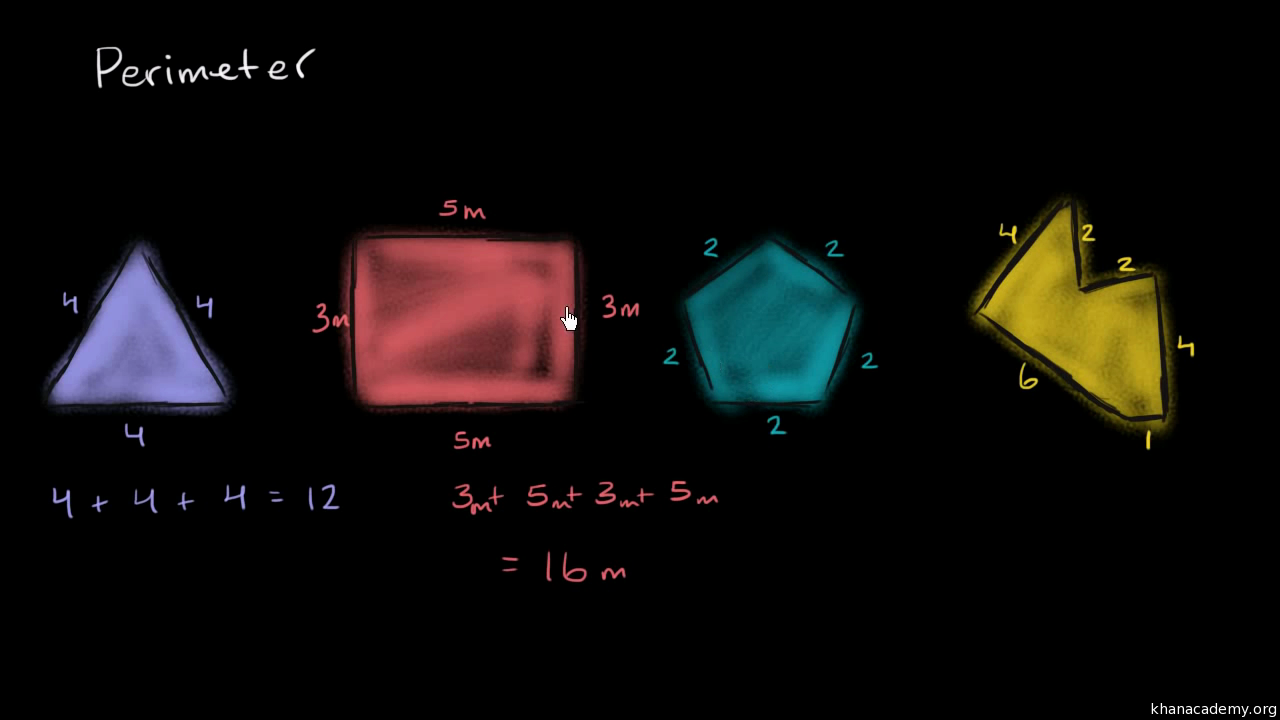
Calculate the Perimeter
The perimeter of a right triangle is the sum of all its sides:
Examples
Example 1: Find the Hypotenuse
Given a right triangle with legs of 3 cm and 4 cm:
Example 2: Find a Side
Given a right triangle with a hypotenuse of 10 cm and one leg of 6 cm:
Additional Uses
The Pythagorean Theorem extends to other areas of mathematics such as trigonometric functions and vector addition, providing a basis for understanding relationships in various mathematical contexts.
READ MORE:
Introduction
The Pythagorean theorem is a fundamental principle in mathematics that establishes a relationship between the sides of a right-angled triangle. The theorem states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This can be expressed mathematically as \(a^2 + b^2 = c^2\), where \(a\) and \(b\) are the legs of the triangle, and \(c\) is the hypotenuse. This relationship allows us to calculate the length of any side of a right triangle if the lengths of the other two sides are known.
Using the Pythagorean theorem, you can also calculate the perimeter of a right-angled triangle, which is the sum of the lengths of all three sides. Additionally, the area of the triangle can be determined using the formula \( \text{Area} = \frac{1}{2} \times a \times b \). These calculations are essential for various applications in fields such as engineering, architecture, and various sciences.
Our Pythagorean theorem calculator simplifies these computations. By entering the known values of any two sides, the calculator quickly finds the third side, the perimeter, and the area of the triangle. This tool is designed to save time and reduce errors, making it invaluable for students and professionals alike.
Understanding the Pythagorean Theorem
The Pythagorean Theorem, attributed to the ancient Greek mathematician Pythagoras, is a fundamental principle in geometry. It states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Mathematically, this is expressed as:
\[ c^2 = a^2 + b^2 \]
where \( c \) is the hypotenuse, and \( a \) and \( b \) are the other two sides. This theorem is crucial for various applications, from construction to navigation, as it allows the calculation of an unknown side length when the other two sides are known.
For example, if you have a right-angled triangle with one side measuring 3 units and the other side measuring 4 units, the length of the hypotenuse can be calculated as:
\[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
The Pythagorean Theorem can also be rearranged to find the length of one of the legs if the hypotenuse and the other leg are known:
\[ a = \sqrt{c^2 - b^2} \]
\[ b = \sqrt{c^2 - a^2} \]
These relationships make the Pythagorean Theorem a powerful tool in various fields.
- Algebraic Proof: By arranging four copies of a right triangle around a square, you can derive the equation by comparing the areas of the resulting shapes.
- Geometric Proof: Comparing the areas of a large square formed by the hypotenuse to the sum of the areas of smaller shapes can also confirm the theorem.
Understanding and applying the Pythagorean Theorem is essential for solving problems involving right-angled triangles, making it a cornerstone of geometry and a practical tool in everyday scenarios.
Basic Formula
The Pythagorean Theorem is a fundamental principle in geometry, particularly for right-angled triangles. The theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. The basic formula is:
\[ a^2 + b^2 = c^2 \]
Where:
- \(a\) is one leg of the triangle
- \(b\) is the other leg of the triangle
- \(c\) is the hypotenuse
Using this formula, you can find the length of any side of a right-angled triangle if the lengths of the other two sides are known.
Finding the Hypotenuse
To find the hypotenuse \(c\), rearrange the formula:
\[ c = \sqrt{a^2 + b^2} \]
For example, if \(a = 3\) and \(b = 4\):
\[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
Finding a Leg
To find a leg when the hypotenuse and the other leg are known:
\[ a = \sqrt{c^2 - b^2} \]
For example, if \(c = 5\) and \(b = 4\):
\[ a = \sqrt{5^2 - 4^2} = \sqrt{25 - 16} = \sqrt{9} = 3 \]
Calculating the Perimeter
The perimeter of a right-angled triangle is the sum of all its sides:
\[ \text{Perimeter} = a + b + c \]
For example, if \(a = 3\), \(b = 4\), and \(c = 5\):
\[ \text{Perimeter} = 3 + 4 + 5 = 12 \]
Area Calculation
The area of a right-angled triangle can be found using the formula:
\[ \text{Area} = \frac{1}{2} \times a \times b \]
For example, if \(a = 3\) and \(b = 4\):
\[ \text{Area} = \frac{1}{2} \times 3 \times 4 = 6 \]
This understanding of the Pythagorean Theorem allows you to solve various problems involving right-angled triangles efficiently.
Calculating the Hypotenuse
The Pythagorean Theorem is a fundamental principle in geometry, providing a method to calculate the length of the hypotenuse in a right triangle. The hypotenuse is the side opposite the right angle, and its length can be determined using the formula:
\[ c = \sqrt{a^2 + b^2} \]
Here is a step-by-step method to calculate the hypotenuse:
- Identify the lengths of the two legs of the triangle. Let's call these \( a \) and \( b \).
- Square the lengths of both legs:
- Add the results of these squares together:
- Take the square root of this sum to find the hypotenuse \( c \):
\[ a^2 \] and \[ b^2 \]
\[ a^2 + b^2 \]
\[ c = \sqrt{a^2 + b^2} \]
For example, if \( a = 6 \) cm and \( b = 8 \) cm, then:
\[ c^2 = 6^2 + 8^2 \]
\[ c^2 = 36 + 64 \]
\[ c^2 = 100 \]
\[ c = \sqrt{100} = 10 \, \text{cm} \]
Therefore, the length of the hypotenuse is 10 cm. This straightforward method can be applied to any right triangle when the lengths of the other two sides are known.

Calculating the Other Sides
To calculate the other sides of a right triangle using the Pythagorean Theorem, follow these steps:
- Identify Known Values: Determine which sides you know. For example, you might know the hypotenuse (c) and one leg (a), and you need to find the other leg (b).
- Use the Pythagorean Theorem Formula: The Pythagorean Theorem is expressed as \(a^2 + b^2 = c^2\). Rearrange this formula to solve for the unknown side.
-
Solving for Side \(a\):
- Rearrange the formula to solve for \(a\): \(a = \sqrt{c^2 - b^2}\).
- Insert the known values and calculate.
- Example: If \(c = 10\) and \(b = 8\), then \(a = \sqrt{10^2 - 8^2} = \sqrt{100 - 64} = \sqrt{36} = 6\).
-
Solving for Side \(b\):
- Rearrange the formula to solve for \(b\): \(b = \sqrt{c^2 - a^2}\).
- Insert the known values and calculate.
- Example: If \(c = 10\) and \(a = 6\), then \(b = \sqrt{10^2 - 6^2} = \sqrt{100 - 36} = \sqrt{64} = 8\).
Using these steps, you can determine the missing sides of any right triangle efficiently. This method is essential for various applications in construction, navigation, and many fields requiring precise measurements.
Perimeter Calculation
The perimeter of a right-angled triangle can be calculated using the Pythagorean theorem and the sum of all sides. Follow these steps to find the perimeter:
- Identify the lengths of the two legs of the right triangle, labeled as a and b.
- Use the Pythagorean theorem to calculate the length of the hypotenuse (c):
- c = √(a2 + b2)
- Sum the lengths of all three sides to find the perimeter:
- Perimeter = a + b + c
Here's a step-by-step example:
| Step | Calculation | Result |
|---|---|---|
| 1 | Identify the lengths of a and b | a = 3, b = 4 |
| 2 | Calculate c using the Pythagorean theorem | c = √(32 + 42) = √(9 + 16) = √25 = 5 |
| 3 | Sum all sides to find the perimeter | Perimeter = 3 + 4 + 5 = 12 |
By following these steps, you can easily calculate the perimeter of any right-angled triangle using the Pythagorean theorem.
Examples and Applications
The Pythagorean theorem has numerous applications in various fields such as mathematics, physics, engineering, and everyday problem-solving. Here are some detailed examples and practical applications of the Pythagorean theorem:
Example 1: Finding the Hypotenuse
Given a right triangle with legs \( a = 3 \) units and \( b = 4 \) units, we can find the hypotenuse \( c \) using the Pythagorean theorem:
Using the formula:
\[
c = \sqrt{a^2 + b^2}
\]
\[
c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \, \text{units}
\]
Example 2: Real-Life Application - Ladder Problem
Imagine you need to place a ladder against a wall. If the ladder is 10 feet long and you place its base 6 feet away from the wall, how high up the wall does the ladder reach?
Using the Pythagorean theorem:
\[
c = 10 \, \text{feet} \quad \text{(ladder length)}
\]
\[
a = 6 \, \text{feet} \quad \text{(distance from the wall)}
\]
\[
b = \sqrt{c^2 - a^2} = \sqrt{10^2 - 6^2} = \sqrt{100 - 36} = \sqrt{64} = 8 \, \text{feet}
\]
The ladder reaches 8 feet up the wall.
Example 3: Distance Between Two Points
The Pythagorean theorem can be used to find the distance between two points on a coordinate plane. Suppose you have points \( (x_1, y_1) = (1, 2) \) and \( (x_2, y_2) = (4, 6) \). The distance \( d \) between these points is:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
\[
d = \sqrt{(4 - 1)^2 + (6 - 2)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \, \text{units}
\]
Applications in Construction and Architecture
- Ensuring structures are level and square by confirming right angles.
- Calculating the lengths of rafters in roofing projects.
- Designing ramps for accessibility where the height and length need to be proportional.
Applications in Navigation
- Determining the shortest path between two points.
- Calculating distances in air and sea navigation.
Example 4: Determining the Diagonal of a Rectangle
Given a rectangle with length \( l = 8 \) units and width \( w = 6 \) units, the diagonal \( d \) can be found as follows:
\[
d = \sqrt{l^2 + w^2}
\]
\[
d = \sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10 \, \text{units}
\]
Advanced Example: 3D Pythagorean Theorem
In three dimensions, the Pythagorean theorem can extend to finding the diagonal of a rectangular prism. For a prism with sides \( a \), \( b \), and \( c \), the diagonal \( d \) is:
\[
d = \sqrt{a^2 + b^2 + c^2}
\]
For example, if \( a = 3 \) units, \( b = 4 \) units, and \( c = 5 \) units, the diagonal is:
\[
d = \sqrt{3^2 + 4^2 + 5^2} = \sqrt{9 + 16 + 25} = \sqrt{50} \approx 7.07 \, \text{units}
\]
These examples illustrate the versatility and usefulness of the Pythagorean theorem in solving various practical problems and theoretical questions.
Proof of the Pythagorean Theorem
The Pythagorean Theorem, a fundamental principle in geometry, can be proven in several ways. Here, we will explore one of the most straightforward and elegant proofs using algebra and geometry.
Algebraic Proof
Consider a right triangle with sides \(a\), \(b\), and hypotenuse \(c\). The theorem states that:
\(a^2 + b^2 = c^2\)
We can prove this by using a geometric approach with a square:
- Construct a large square with side length \(a + b\).
- Inside this square, place four identical right triangles with legs \(a\) and \(b\), and hypotenuse \(c\), such that they form a smaller tilted square in the center.
The area of the large square can be calculated in two ways:
- By summing the areas of the four triangles and the smaller central square.
- Directly from the side length of the large square.
First, calculate the area of the large square:
Area = \((a + b)^2\)
Now, calculate the total area from the components:
- Area of the smaller square = \(c^2\)
- Area of each triangle = \(\frac{1}{2}ab\)
- Area of four triangles = \(4 \cdot \frac{1}{2}ab = 2ab\)
Thus, the total area is:
\(c^2 + 2ab\)
Since both expressions represent the area of the same large square, we can equate them:
\((a + b)^2 = c^2 + 2ab\)
Expanding the left-hand side:
\(a^2 + 2ab + b^2 = c^2 + 2ab\)
By subtracting \(2ab\) from both sides, we obtain:
\(a^2 + b^2 = c^2\)
This completes the algebraic proof of the Pythagorean Theorem.
Geometric Proof
Another way to prove the Pythagorean Theorem is through geometric dissection:
- Consider a square with side length \(c\).
- Within this square, inscribe four right triangles with legs \(a\) and \(b\) and hypotenuse \(c\), arranged such that their hypotenuses form a smaller square inside.
- The area of the large square is \(c^2\).
- The area of the smaller square formed by the hypotenuses is \((c-b)^2\) and the four right triangles form the remaining area.
By calculating and equating the areas of these regions, we can derive the same relationship, proving \(a^2 + b^2 = c^2\).
Conclusion
These proofs highlight the elegance and simplicity of the Pythagorean Theorem. Understanding these proofs not only reinforces the theorem itself but also demonstrates the power of algebraic and geometric reasoning in mathematics.

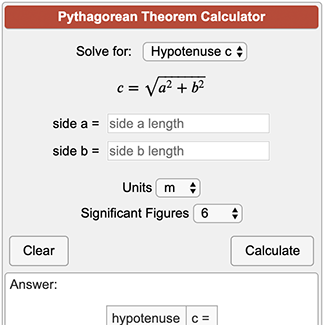
Using the Calculator
Using a Pythagorean Theorem calculator simplifies finding the lengths of sides in right triangles and other related calculations. Here are the steps to use the calculator effectively:
-
Enter Known Values: Input the known values of the two sides. These sides are typically labeled as \(a\) and \(b\) (the legs) or \(a\) and \(c\) (where \(c\) is the hypotenuse).
-
Select the Calculation Type: Choose what you want to calculate. You can solve for the missing side (\(a\), \(b\), or \(c\)), the area of the triangle, or the perimeter.
-
Press Calculate: Click the "Calculate" button to get the result. The calculator will use the Pythagorean theorem formula:
\[
c = \sqrt{a^2 + b^2}
\]for the hypotenuse, or:
\[
a = \sqrt{c^2 - b^2} \quad \text{or} \quad b = \sqrt{c^2 - a^2}
\]for the other sides.
-
View Detailed Solution: Some calculators provide step-by-step solutions to show how the result was derived. This can be helpful for learning and verification purposes.
-
Additional Features: Many calculators also offer additional calculations such as finding angles, area, and perimeter. For instance:
- Calculate the area of the triangle using: \[ A = \frac{1}{2}ab \]
- Calculate the perimeter by adding all sides: \[ P = a + b + c
These steps will help you efficiently use a Pythagorean theorem calculator to solve various geometric problems involving right triangles.
Related Calculations
The Pythagorean theorem serves as the foundation for several related calculations in geometry and trigonometry. Here are some important calculations and applications derived from the Pythagorean theorem:
1. Area Calculation
The area of a right triangle can be calculated using the lengths of the two legs. The formula for the area \( A \) is:
\[
A = \frac{1}{2} \times a \times b
\]
Where \( a \) and \( b \) are the lengths of the legs of the right triangle.
2. Angle Calculation
The angles in a right triangle can be found using trigonometric functions. If you know the lengths of the sides, you can calculate the angles \( \alpha \) and \( \beta \) as follows:
-
\( \alpha = \arcsin \left(\frac{a}{c}\right) \) or \( \alpha = \arccos \left(\frac{b}{c}\right) \)
-
\( \beta = \arcsin \left(\frac{b}{c}\right) \) or \( \beta = \arccos \left(\frac{a}{c}\right) \)
Where \( c \) is the hypotenuse of the right triangle.
3. Height Calculation
The height \( h \) of a right triangle, perpendicular to the hypotenuse, can be calculated if the lengths of the legs are known:
\[
h = \frac{a \times b}{c}
\]
Where \( c \) is the hypotenuse, and \( a \) and \( b \) are the legs.
4. Perimeter Calculation
The perimeter \( P \) of a right triangle is the sum of the lengths of all three sides:
\[
P = a + b + c
\]
This is useful in various practical applications, such as determining the amount of material needed for construction.
5. Pythagorean Triples
Pythagorean triples are sets of three positive integers \( a \), \( b \), and \( c \) that satisfy the equation \( a^2 + b^2 = c^2 \). A common example is the set (3, 4, 5).
These triples are useful in problems where integer solutions are required, and they often appear in different areas of number theory and geometry.
6. Real-life Applications
Architecture: Ensuring that building structures have accurate right angles.
Navigation: Calculating shortest paths and distances, especially in mapping and GPS technology.
Engineering: Designing components that require precise measurements and angles.
Common Problems and Solutions
Problem: Difficulty in identifying the correct values for the sides of the triangle.
Solution: Ensure that you correctly identify which side is the hypotenuse and which are the other two sides. Remember, the hypotenuse is always opposite the right angle.
Problem: Incorrect application of the Pythagorean theorem formula.
Solution: Double-check your calculations and ensure that you square the lengths of both legs of the right triangle and then add them together to find the square of the hypotenuse.
Problem: Obtaining a negative result when calculating side lengths.
Solution: Negative results can occur when the measurements are incorrectly applied. Reassess your measurements and ensure they are accurately represented in the formula.
Problem: Dealing with decimals or fractions in calculations.
Solution: When working with decimals or fractions, it's crucial to maintain precision throughout your calculations. Consider rounding to an appropriate decimal place or converting fractions to decimals before proceeding with the calculation.
Problem: Handling non-right triangles.
Solution: The Pythagorean theorem only applies to right triangles. For non-right triangles, alternative methods such as the Law of Sines or Law of Cosines may be required.
Advanced Applications
Exploring the 3D Pythagorean Theorem:
Extend your understanding of the Pythagorean theorem into three-dimensional space. This involves finding the distance between two points in 3D space using the formula:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \]
where \((x_1, y_1, z_1)\) and \((x_2, y_2, z_2)\) are the coordinates of two points in space.
Applying the Pythagorean theorem to complex geometric shapes:
Extend your knowledge beyond simple right triangles and explore how the Pythagorean theorem can be applied to more complex geometric shapes. This may involve decomposing the shape into smaller right triangles or utilizing trigonometric functions to find missing lengths.

Frequently Asked Questions
What is the Pythagorean theorem?
The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
How do I find the perimeter of a triangle using the Pythagorean theorem?
To find the perimeter of a right triangle, you would first calculate the lengths of all three sides using the Pythagorean theorem, then add these lengths together to obtain the perimeter.
Can the Pythagorean theorem be applied to non-right triangles?
No, the Pythagorean theorem only applies to right-angled triangles. For non-right triangles, alternative methods such as the Law of Sines or Law of Cosines must be used to find side lengths or angles.
What should I do if I encounter negative results when applying the Pythagorean theorem?
If you obtain negative results, it may indicate an error in your measurements or calculations. Double-check your inputs and calculations to ensure accuracy.
Are there any practical applications of the Pythagorean theorem?
Yes, the Pythagorean theorem has numerous practical applications in various fields such as engineering, architecture, physics, and computer graphics. It is commonly used to solve problems involving distance, such as finding the shortest distance between two points.
Resources and Further Reading
MathIsFun - Pythagorean Theorem: A comprehensive guide to understanding the Pythagorean theorem with interactive explanations and examples.
Link:
Khan Academy - Pythagorean Theorem: Video tutorials and practice exercises to deepen your understanding of the Pythagorean theorem.
Link:
Wolfram MathWorld - Pythagorean Theorem: In-depth explanations, formulas, and applications of the Pythagorean theorem.
Link:
Geogebra - Interactive Pythagorean Theorem Calculator: A tool for visually exploring the Pythagorean theorem and solving related problems.
Link:
Video hướng dẫn cách sử dụng Định lý Pythagoras để tính chu vi của các hình tam giác.
Tìm Chu vi bằng Định lý Pythagoras (video)
READ MORE:
Video hướng dẫn cách sử dụng Định lý Pythagoras để tìm độ dài của một cạnh thiếu trong các hình tam giác.
Định lý Pythagoras: Tìm Độ Dài của Một Cạnh Thiếu | Toán cùng thầy J