Topic polygon perimeter: Discover everything you need to know about polygon perimeters in this comprehensive guide. From basic concepts and formulas to advanced applications and real-world examples, learn how to calculate and understand the perimeter of various polygons effectively. Perfect for students, educators, and professionals alike, this article will enhance your geometric knowledge and skills.
Table of Content
- Polygon Perimeter
- Introduction to Polygon Perimeter
- Definition and Basic Concepts
- General Formula for Perimeter Calculation
- Perimeter of Regular Polygons
- Perimeter of Irregular Polygons
- Perimeter Calculation Examples
- Perimeter of Common Polygons
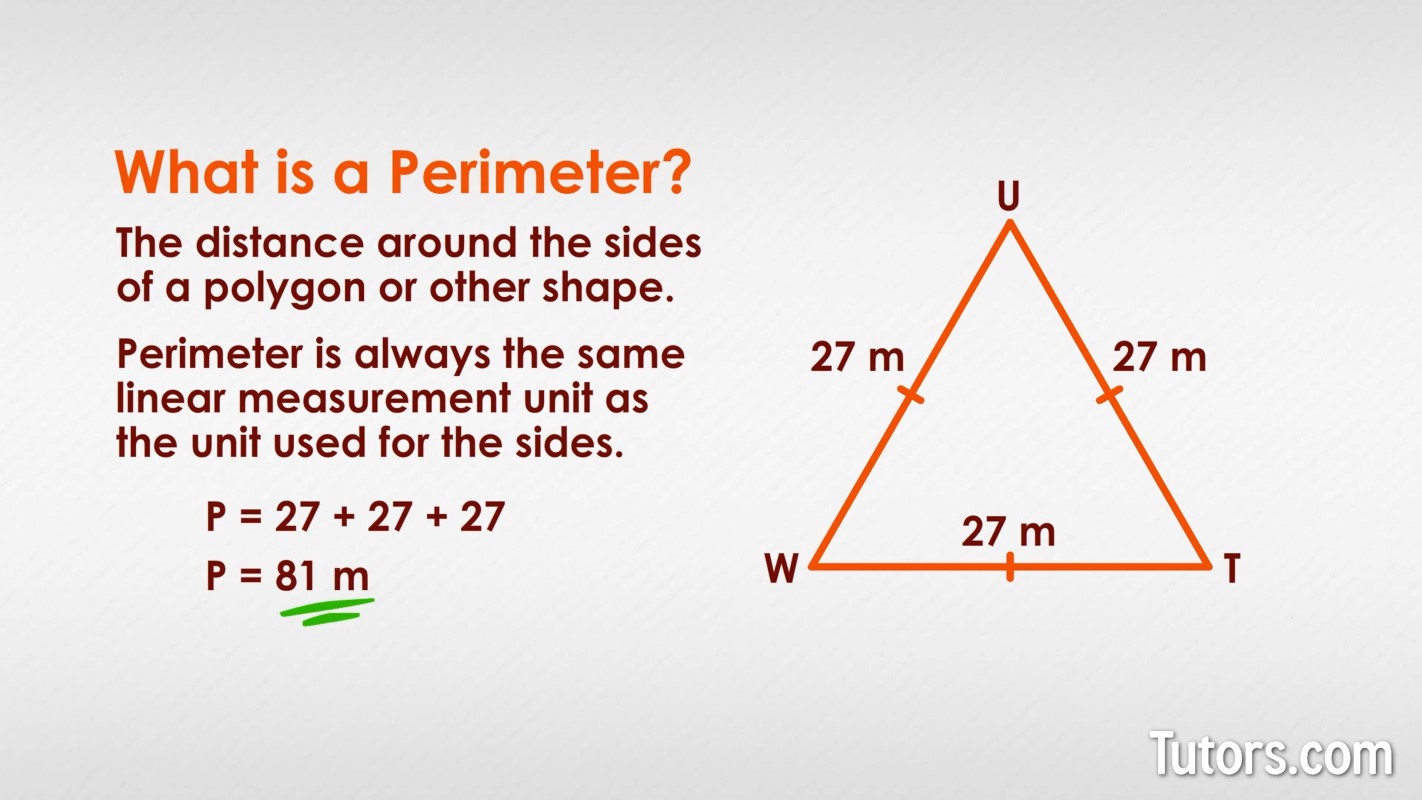
- Equilateral Triangle
- Square
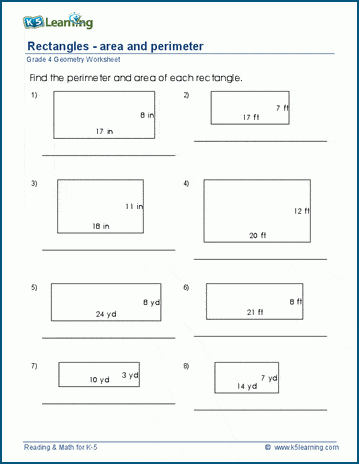
- Rectangle
- Pentagon
- Hexagon
- Applications of Perimeter Calculations
- Urban Planning and Construction
- Agricultural Uses
- Geometric and Engineering Applications
- Tools and Techniques for Measuring Perimeter
- Perimeter and Area: Differences and Relationships
- YOUTUBE:
Polygon Perimeter
The perimeter of a polygon is the total length of its sides. To calculate the perimeter, you need to sum the lengths of all the sides. The formula to find the perimeter depends on the type of polygon and the information available.
General Formula
If a polygon has \(n\) sides with lengths \(a_1, a_2, a_3, \ldots, a_n\), the perimeter \(P\) is given by:
\(P = a_1 + a_2 + a_3 + \cdots + a_n\)
Regular Polygons
A regular polygon has all sides of equal length. If the length of each side is \(a\) and the polygon has \(n\) sides, the perimeter \(P\) is:
\(P = n \cdot a\)
Example Calculations
- Triangle
- For an equilateral triangle with side length \(a\):
- \(P = 3a\)
- For a triangle with sides \(a, b, c\):
- \(P = a + b + c\)
- Square
- For a square with side length \(a\):
- \(P = 4a\)
- Rectangle
- For a rectangle with length \(l\) and width \(w\):
- \(P = 2l + 2w\)
- Pentagon
- For a regular pentagon with side length \(a\):
- \(P = 5a\)
- Hexagon
- For a regular hexagon with side length \(a\):
- \(P = 6a\)
Irregular Polygons
For an irregular polygon, sum the lengths of all sides to get the perimeter:
\(P = a_1 + a_2 + a_3 + \cdots + a_n\)
Practical Applications
- Urban planning and construction projects often require perimeter calculations for boundary definitions.
- In agriculture, calculating the perimeter of land plots helps in fencing and resource allocation.
- Perimeter measurements are essential in various fields such as geometry, physics, and engineering.

READ MORE:
Introduction to Polygon Perimeter
A polygon is a closed, two-dimensional shape with straight sides. The perimeter of a polygon is the total distance around its edges. Understanding the concept of the perimeter is fundamental in geometry and has practical applications in various fields such as construction, urban planning, and agriculture. This section provides a detailed introduction to the perimeter of polygons, covering basic definitions, types of polygons, and step-by-step methods for calculating the perimeter.
The perimeter is calculated by summing the lengths of all sides of the polygon. Different types of polygons, such as regular and irregular polygons, have specific methods for perimeter calculation.
Basic Definitions
- Polygon: A closed figure formed by a finite number of straight line segments.
- Side: Each straight line segment of a polygon.
- Vertex: The point where two sides of a polygon meet.
- Perimeter: The total length of all sides of a polygon.
Types of Polygons
Polygons can be classified based on the number of sides and the equality of their side lengths and angles:
- Regular Polygon: All sides and angles are equal (e.g., equilateral triangle, square).
- Irregular Polygon: Sides and angles are not necessarily equal.
- Convex Polygon: All interior angles are less than 180 degrees.
- Concave Polygon: At least one interior angle is greater than 180 degrees.
Calculating the Perimeter
The method for calculating the perimeter depends on the type of polygon:
- Regular Polygon: Multiply the length of one side by the total number of sides.
\(P = n \cdot a\)
where \(n\) is the number of sides and \(a\) is the length of one side.
- Irregular Polygon: Sum the lengths of all sides.
\(P = a_1 + a_2 + a_3 + \cdots + a_n\)
where \(a_1, a_2, a_3, \ldots, a_n\) are the lengths of the sides.
Understanding these basics is essential for more complex geometric calculations and real-world applications. The following sections will delve deeper into specific examples and advanced topics related to polygon perimeters.
Definition and Basic Concepts
The perimeter of a polygon is the total length of its boundaries. It is a fundamental concept in geometry, used to measure the distance around a two-dimensional shape. Understanding the perimeter helps in various applications, from simple geometric problems to real-world scenarios such as fencing a plot of land.
Definition
A polygon is a plane figure that is described by a finite number of straight line segments connected to form a closed chain or circuit. These segments are called sides or edges, and the points where two edges meet are the polygon's vertices or corners. The perimeter is the sum of the lengths of these edges.
Basic Concepts
- Vertices (Singular: Vertex): The points where two sides of a polygon meet.
- Sides (or Edges): The straight line segments that make up the polygon.
- Perimeter (P): The total distance around the polygon, calculated by adding the lengths of all sides.
Formula for Perimeter
The formula for the perimeter depends on the type of polygon:
- Regular Polygon: A regular polygon has all sides of equal length and all interior angles equal.
\(P = n \cdot a\)
where \(n\) is the number of sides and \(a\) is the length of one side.
- Irregular Polygon: An irregular polygon has sides of different lengths.
\(P = a_1 + a_2 + a_3 + \cdots + a_n\)
where \(a_1, a_2, a_3, \ldots, a_n\) are the lengths of the sides.
Examples
- Triangle: For a triangle with sides \(a, b, c\):
\(P = a + b + c\)
- Square: For a square with side length \(a\):
\(P = 4a\)
- Rectangle: For a rectangle with length \(l\) and width \(w\):
\(P = 2l + 2w\)
Understanding these basic concepts and formulas is crucial for solving more complex geometric problems and for practical applications in fields such as architecture, engineering, and various design disciplines.
General Formula for Perimeter Calculation
Calculating the perimeter of a polygon involves summing the lengths of its sides. The specific formula used depends on whether the polygon is regular (all sides and angles are equal) or irregular (sides and angles are not necessarily equal). Below, we outline the general formulas and methods for both types of polygons.
Regular Polygons
A regular polygon has equal side lengths and equal interior angles. The formula for the perimeter \(P\) of a regular polygon is:
\(P = n \cdot a\)
where:
- \(n\) is the number of sides
- \(a\) is the length of one side
For example, for a regular hexagon with side length \(a\):
\(P = 6a\)
Irregular Polygons
An irregular polygon has sides of different lengths. The perimeter \(P\) of an irregular polygon is the sum of the lengths of all its sides:
\(P = a_1 + a_2 + a_3 + \cdots + a_n\)
where:
- \(a_1, a_2, a_3, \ldots, a_n\) are the lengths of the sides
For example, for an irregular quadrilateral with side lengths \(a, b, c, d\):
\(P = a + b + c + d\)
Examples
- Triangle: For a triangle with sides \(a, b, c\):
\(P = a + b + c\)
- Square: For a square with side length \(a\):
\(P = 4a\)
- Rectangle: For a rectangle with length \(l\) and width \(w\):
\(P = 2l + 2w\)
Step-by-Step Calculation
- Identify the type of polygon: Determine whether the polygon is regular or irregular.
- Measure the sides: Accurately measure the length of each side of the polygon.
- Apply the formula: Use the appropriate formula based on the type of polygon:
- For regular polygons, use \(P = n \cdot a\)
- For irregular polygons, use \(P = a_1 + a_2 + a_3 + \cdots + a_n\)
- Sum the lengths: Add the lengths of all sides to get the perimeter.
These general formulas and steps provide a clear method for calculating the perimeter of any polygon, whether regular or irregular. Mastery of these techniques is essential for solving more advanced geometric problems and practical applications in various fields.
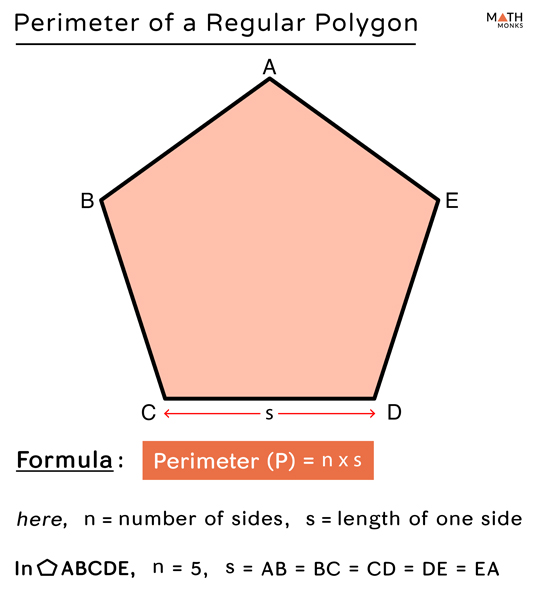
Perimeter of Regular Polygons
A regular polygon is a polygon with all sides and angles equal. Calculating the perimeter of a regular polygon is straightforward due to the uniformity of its sides. Below, we provide a detailed explanation of the formula and step-by-step methods for calculating the perimeter of various regular polygons.
General Formula
The perimeter \(P\) of a regular polygon can be calculated using the formula:
\(P = n \cdot a\)
where:
- \(n\) is the number of sides
- \(a\) is the length of one side
Examples
- Equilateral Triangle: An equilateral triangle has three equal sides.
\(P = 3a\)
where \(a\) is the length of one side.
- Square: A square has four equal sides.
\(P = 4a\)
where \(a\) is the length of one side.
- Regular Pentagon: A regular pentagon has five equal sides.
\(P = 5a\)
where \(a\) is the length of one side.
- Regular Hexagon: A regular hexagon has six equal sides.
\(P = 6a\)
where \(a\) is the length of one side.
Step-by-Step Calculation
- Identify the number of sides: Determine the number of sides \(n\) of the regular polygon.
- Measure one side: Measure the length \(a\) of one side of the polygon.
- Apply the formula: Use the formula \(P = n \cdot a\) to calculate the perimeter.
- Calculate the perimeter: Multiply the number of sides by the length of one side to obtain the perimeter.
Special Cases
For some regular polygons, specific names and properties apply:
- Equilateral Triangle: Each angle measures \(60^\circ\) and the perimeter is \(3a\).
- Square: Each angle measures \(90^\circ\) and the perimeter is \(4a\).
- Regular Pentagon: Each angle measures \(108^\circ\) and the perimeter is \(5a\).
- Regular Hexagon: Each angle measures \(120^\circ\) and the perimeter is \(6a\).
Understanding the perimeter of regular polygons is essential for solving various geometric problems and has practical applications in designing symmetrical structures and patterns.

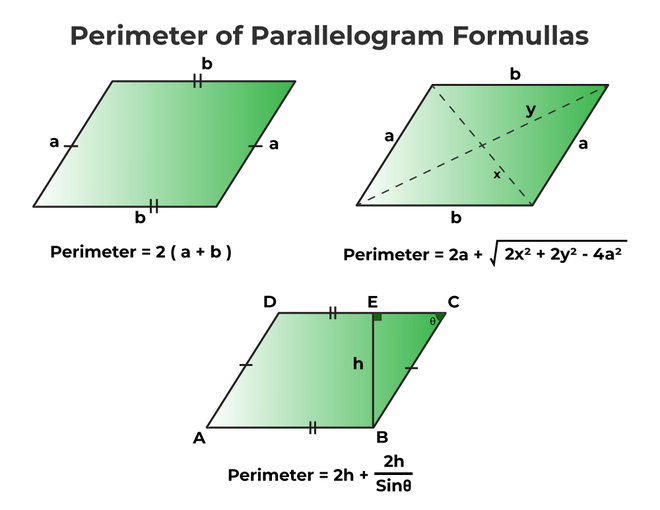
Perimeter of Irregular Polygons
The perimeter of an irregular polygon, unlike regular polygons, does not have equal side lengths. To find the perimeter of an irregular polygon, one must sum the lengths of all its sides. The steps to calculate the perimeter are as follows:
- Identify the Side Lengths: Measure or identify the lengths of each side of the polygon. These can be given directly or calculated using the distance formula for coordinates.
- Sum the Side Lengths: Add together the lengths of all the sides to get the perimeter.
The formula for the perimeter \( P \) of an irregular polygon with side lengths \( a_1, a_2, a_3, \ldots, a_n \) is:
\[ P = a_1 + a_2 + a_3 + \cdots + a_n \]
Example Calculation
Consider an irregular polygon with the following side lengths:
- Side 1: 4 cm
- Side 2: 5 cm
- Side 3: 6 cm
- Side 4: 7 cm
The perimeter \( P \) can be calculated as:
\[ P = 4 \, \text{cm} + 5 \, \text{cm} + 6 \, \text{cm} + 7 \, \text{cm} = 22 \, \text{cm} \]
Using Coordinate Geometry
For an irregular polygon with vertices at \((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\), the perimeter can be calculated using the distance formula:
The distance between two points \((x_i, y_i)\) and \((x_{i+1}, y_{i+1})\) is given by:
\[ d_i = \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} \]
Then, the perimeter \( P \) is:
\[ P = \sum_{i=1}^{n} d_i \]
Example Calculation with Coordinates
Consider a polygon with vertices at \((1, 1), (4, 1), (4, 5), (1, 5)\):
| Distance \(d_1\) between (1, 1) and (4, 1): | \[ d_1 = \sqrt{(4 - 1)^2 + (1 - 1)^2} = \sqrt{3^2 + 0^2} = 3 \, \text{units} \] |
| Distance \(d_2\) between (4, 1) and (4, 5): | \[ d_2 = \sqrt{(4 - 4)^2 + (5 - 1)^2} = \sqrt{0^2 + 4^2} = 4 \, \text{units} \] |
| Distance \(d_3\) between (4, 5) and (1, 5): | \[ d_3 = \sqrt{(1 - 4)^2 + (5 - 5)^2} = \sqrt{(-3)^2 + 0^2} = 3 \, \text{units} \] |
| Distance \(d_4\) between (1, 5) and (1, 1): | \[ d_4 = \sqrt{(1 - 1)^2 + (1 - 5)^2} = \sqrt{0^2 + (-4)^2} = 4 \, \text{units} \] |
The perimeter \( P \) is:
\[ P = d_1 + d_2 + d_3 + d_4 = 3 + 4 + 3 + 4 = 14 \, \text{units} \]
Practical Applications
Calculating the perimeter of irregular polygons is crucial in various fields such as:
- Architecture and Construction: Determining the boundary lengths for planning and materials estimation.
- Land Surveying: Measuring plot boundaries and land division.
- Environmental Science: Assessing perimeters of natural features like lakes and forests.
Perimeter Calculation Examples
Calculating the perimeter of various polygons can help solidify understanding of the concepts and formulas involved. Here are several examples:
Example 1: Perimeter of a Regular Pentagon
Consider a regular pentagon where each side is 6 cm long. The perimeter \( P \) of a regular polygon can be calculated using the formula:
\( P = n \times s \)
where \( n \) is the number of sides and \( s \) is the length of each side.
For a pentagon:
\( P = 5 \times 6 = 30 \) cm
Example 2: Perimeter of an Irregular Quadrilateral
Consider a quadrilateral with sides measuring 8 m, 5 m, 7 m, and 10 m. The perimeter is simply the sum of all side lengths:
\( P = 8 + 5 + 7 + 10 = 30 \) m
Example 3: Perimeter of a Regular Hexagon
A regular hexagon has all sides equal. If each side is 4 cm, then the perimeter can be calculated as:
\( P = 6 \times 4 = 24 \) cm
Example 4: Perimeter of an Irregular Pentagon
Consider an irregular pentagon with the following side lengths: 3 cm, 4 cm, 5 cm, 6 cm, and 7 cm. The perimeter is:
\( P = 3 + 4 + 5 + 6 + 7 = 25 \) cm
Example 5: Perimeter of a Compound Shape
Imagine a shape made by combining a rectangle and a triangle. The rectangle has a length of 8 cm and a width of 3 cm. The triangle is an equilateral triangle with a side length of 3 cm. First, calculate the perimeter of each individual shape:
- Perimeter of the rectangle:
- Perimeter of the equilateral triangle:
\( P = 2 \times (8 + 3) = 2 \times 11 = 22 \) cm
\( P = 3 \times 3 = 9 \) cm
Since one side of the triangle is shared with the rectangle, subtract this side length from the total perimeter:
\( P_{\text{total}} = 22 + 9 - 3 = 28 \) cm
Example 6: Perimeter in a Real-World Context
Consider a garden in the shape of an irregular hexagon with the following side lengths: 15 m, 12 m, 10 m, 18 m, 16 m, and 20 m. To find the perimeter:
\( P = 15 + 12 + 10 + 18 + 16 + 20 = 91 \) m
Example 7: Perimeter Using Coordinates
For a polygon with vertices at coordinates \( (0,0) \), \( (4,0) \), \( (4,3) \), and \( (0,3) \) (a rectangle), calculate the perimeter by determining the distance between consecutive points:
- Distance between \( (0,0) \) and \( (4,0) \): 4 units
- Distance between \( (4,0) \) and \( (4,3) \): 3 units
- Distance between \( (4,3) \) and \( (0,3) \): 4 units
- Distance between \( (0,3) \) and \( (0,0) \): 3 units
Adding these distances gives the perimeter:
\( P = 4 + 3 + 4 + 3 = 14 \) units
Perimeter of Common Polygons
The perimeter of a polygon is the total distance around its edges. Here, we will discuss how to calculate the perimeter of various common polygons including triangles, squares, rectangles, and more.
Equilateral Triangle
An equilateral triangle has all three sides of equal length. The formula for its perimeter is:
\[ \text{Perimeter} = 3a \]
where \( a \) is the length of one side.
Example: If the side length is 5 units, the perimeter is \( 3 \times 5 = 15 \) units.
Square
A square has all four sides of equal length. The formula for its perimeter is:
\[ \text{Perimeter} = 4a \]
where \( a \) is the length of one side.
Example: If the side length is 4 units, the perimeter is \( 4 \times 4 = 16 \) units.
Rectangle
A rectangle has opposite sides of equal length. The formula for its perimeter is:
\[ \text{Perimeter} = 2l + 2w \]
where \( l \) is the length and \( w \) is the width.
Example: If the length is 6 units and the width is 3 units, the perimeter is \( 2 \times 6 + 2 \times 3 = 18 \) units.
Pentagon
A regular pentagon has five sides of equal length. The formula for its perimeter is:
\[ \text{Perimeter} = 5a \]
where \( a \) is the length of one side.
Example: If the side length is 7 units, the perimeter is \( 5 \times 7 = 35 \) units.
Hexagon
A regular hexagon has six sides of equal length. The formula for its perimeter is:
\[ \text{Perimeter} = 6a \]
where \( a \) is the length of one side.
Example: If the side length is 8 units, the perimeter is \( 6 \times 8 = 48 \) units.
Irregular Polygons
For irregular polygons, where sides may have different lengths, the perimeter is calculated by simply adding the lengths of all sides:
\[ \text{Perimeter} = a_1 + a_2 + a_3 + \ldots + a_n \]
where \( a_1, a_2, a_3, \ldots, a_n \) are the lengths of the sides.
Example: For a polygon with side lengths of 3 units, 4 units, 5 units, and 6 units, the perimeter is \( 3 + 4 + 5 + 6 = 18 \) units.
Equilateral Triangle
An equilateral triangle is a special type of triangle where all three sides are of equal length and all three interior angles are equal to 60 degrees. The properties of equilateral triangles make their perimeter calculations straightforward.
Properties of an Equilateral Triangle
- All three sides are equal in length: \(a = b = c\)
- All three angles are equal to 60 degrees: \(\angle A = \angle B = \angle C = 60^\circ\)
- Each exterior angle is 120 degrees.
Perimeter Calculation
The perimeter \(P\) of an equilateral triangle is simply the sum of its three equal sides. The formula for the perimeter is:
\( P = 3a \)
Where \(a\) is the length of one side of the equilateral triangle.
Example Calculation
Consider an equilateral triangle with each side of length 5 cm. To find the perimeter:
\( P = 3 \times 5 \, \text{cm} = 15 \, \text{cm} \)
Height and Area Calculation
The height \(h\) of an equilateral triangle can be calculated using the Pythagorean theorem. Since the altitude divides the triangle into two 30-60-90 right triangles, the height formula is:
\( h = \frac{\sqrt{3}}{2}a \)
The area \(A\) of an equilateral triangle is given by the formula:
\( A = \frac{\sqrt{3}}{4}a^2 \)
Example Calculation
For an equilateral triangle with a side length of 6 cm:
- Calculate the height:
- Calculate the area:
\( h = \frac{\sqrt{3}}{2} \times 6 \, \text{cm} = 3\sqrt{3} \, \text{cm} \approx 5.2 \, \text{cm} \)
\( A = \frac{\sqrt{3}}{4} \times (6 \, \text{cm})^2 = 9\sqrt{3} \, \text{cm}^2 \approx 15.6 \, \text{cm}^2 \)
Summary
To summarize, the key formulas for an equilateral triangle with side length \(a\) are:
- Perimeter: \( P = 3a \)
- Height: \( h = \frac{\sqrt{3}}{2}a \)
- Area: \( A = \frac{\sqrt{3}}{4}a^2 \)
These properties make equilateral triangles unique and easy to work with in geometric calculations.

Square
A square is a special type of polygon where all four sides are of equal length. Calculating the perimeter of a square is straightforward due to its regular shape. The formula for the perimeter \( P \) of a square with side length \( s \) is:
\( P = 4s \)
This formula simply adds the length of all four sides of the square.
Examples
- Example 1: If the side length of a square is 5 cm, its perimeter is calculated as follows:
\( P = 4 \times 5 = 20 \) cm
- Example 2: If the side length of a square is 12 m, the perimeter is:
\( P = 4 \times 12 = 48 \) m
- Example 3: To find the perimeter of a square with an area of 64 square inches, we first find the side length:
- Calculate the side length \( s \) from the area \( A \):
- Then, use the side length to find the perimeter:
\( s = \sqrt{A} = \sqrt{64} = 8 \) inches
\( P = 4 \times 8 = 32 \) inches
- Example 4: If the diagonal of a square is given as 10 cm, we can find the side length using the diagonal formula \( s = \frac{d}{\sqrt{2}} \), where \( d \) is the diagonal:
- Calculate the side length:
- Then, find the perimeter:
\( s = \frac{10}{\sqrt{2}} = \frac{10}{1.414} \approx 7.07 \) cm
\( P = 4 \times 7.07 \approx 28.28 \) cm
Practice Problems
- What is the perimeter of a square with a side length of 11 cm?
- If each side of a square is 5.5 cm, calculate its perimeter.
- The diagonal of a square is 9 cm. Find its perimeter. (Use \( \sqrt{2} \approx 1.414 \))
- If the area of a square is 100 square inches, find its perimeter.
Rectangle
The perimeter of a rectangle is the total length of all its sides. Since opposite sides of a rectangle are equal in length, the formula to calculate the perimeter is straightforward.
Formula
The formula for the perimeter of a rectangle is:
\[ P = 2(l + w) \]
where \( P \) is the perimeter, \( l \) is the length, and \( w \) is the width of the rectangle.
Step-by-Step Calculation
To find the perimeter of a rectangle, follow these steps:
- Measure the length \( l \) of the rectangle.
- Measure the width \( w \) of the rectangle.
- Add the length and the width: \( l + w \).
- Multiply the sum by 2: \( P = 2(l + w) \).
Examples
-
Example 1:
Given a rectangle with a length of 8 meters and a width of 3 meters, the perimeter is calculated as:
\[
P = 2(8 + 3) = 2 \times 11 = 22 \text{ meters}
\] -
Example 2:
For a rectangle with a length of 15 cm and a width of 10 cm, the perimeter calculation is:
\[
P = 2(15 + 10) = 2 \times 25 = 50 \text{ cm}
\] -
Example 3:
If a rectangular field has a length of 120 feet and a width of 75 feet, the perimeter is:
\[
P = 2(120 + 75) = 2 \times 195 = 390 \text{ feet}
\]
Applications
Knowing the perimeter of a rectangle can be useful in various real-world situations:
- Determining the length of fencing needed to surround a rectangular garden.
- Calculating the amount of trim required to go around a rectangular room.
- Finding out how much material is needed to frame a rectangular painting.
Pentagon
A pentagon is a five-sided polygon. The perimeter of a pentagon can be calculated by summing the lengths of all its sides. Depending on whether the pentagon is regular (all sides and angles are equal) or irregular (sides and angles are not equal), the approach to finding the perimeter will differ.
Perimeter of a Regular Pentagon
In a regular pentagon, all five sides are of equal length. If each side is denoted as s, the perimeter P of the pentagon is given by:
\( P = 5s \)
For example, if each side of a regular pentagon is 6 units, the perimeter will be:
\( P = 5 \times 6 = 30 \text{ units} \)
Perimeter of an Irregular Pentagon
In an irregular pentagon, the sides have different lengths. To find the perimeter, simply add the lengths of all five sides. If the sides are denoted as \( a, b, c, d, \) and \( e \), the perimeter P is given by:
\( P = a + b + c + d + e \)
For instance, if the side lengths of an irregular pentagon are 3 units, 4 units, 5 units, 6 units, and 7 units, the perimeter will be:
\( P = 3 + 4 + 5 + 6 + 7 = 25 \text{ units} \)
Example Calculation
Consider a regular pentagon where each side measures 8 units:
- Identify the length of one side: \( s = 8 \text{ units} \)
- Multiply by the number of sides (5): \( P = 5 \times 8 \)
- Calculate the perimeter: \( P = 40 \text{ units} \)
Thus, the perimeter of the pentagon is 40 units.
Applications
- Architecture: Regular pentagons are often used in architectural designs and structures due to their aesthetic appeal.
- Mathematical Problems: Problems involving the perimeter of pentagons help in understanding polygon properties and calculations.
- Art and Design: The shape of a pentagon is widely used in art and design, including logos and patterns.
Interactive Tool for Perimeter Calculation
Use the following table to input the side lengths of an irregular pentagon and calculate the perimeter:
| Side | Length (units) |
|---|---|
| Side 1 | |
| Side 2 | |
| Side 3 | |
| Side 4 | |
| Side 5 | |
| Perimeter | 0 units |
Hexagon
A hexagon is a six-sided polygon with various unique properties and applications. In this section, we will explore the characteristics of hexagons, including their types, properties, and methods to calculate their perimeter.
Types of Hexagons
- Regular Hexagon: All six sides and interior angles are equal. Each interior angle is \(120^\circ\), and the exterior angle is \(60^\circ\).
- Irregular Hexagon: Sides and angles are not equal. The sum of the interior angles is still \(720^\circ\).
- Convex Hexagon: All interior angles are less than \(180^\circ\), and all vertices point outwards.
- Concave Hexagon: At least one interior angle is greater than \(180^\circ\), and at least one vertex points inwards.
Properties of Hexagons
- It has six sides, six edges, and six vertices.
- The sum of the interior angles is \(720^\circ\).
- In a regular hexagon, all sides are equal in length, and all interior angles are \(120^\circ\).
- It has nine diagonals.
- A regular hexagon can be divided into six equilateral triangles.
- Opposite sides of a regular hexagon are parallel.
- Regular hexagons exhibit both rotational and reflectional symmetry.
Perimeter of a Hexagon
The perimeter of a hexagon is the sum of the lengths of all its sides. For a regular hexagon, this can be simplified using the formula:
\[
\text{Perimeter} = 6 \times s
\]
where \(s\) is the length of one side.
For an irregular hexagon, the perimeter is calculated by summing the lengths of all its sides:
\[
\text{Perimeter} = AB + BC + CD + DE + EF + FA
\]
Example Calculation
Consider a regular hexagon where each side is 8 units long. The perimeter \(P\) is calculated as:
\[
P = 6 \times 8 = 48 \text{ units}
\]
Hexagons in Real Life
Hexagons are commonly found in nature and human-made structures. Examples include honeycombs, which maximize efficiency in space usage and structural strength, and various architectural designs that use hexagonal tiles for aesthetic and functional purposes.
Applications of Perimeter Calculations
The concept of perimeter is widely used in various real-life applications, ranging from simple tasks to complex engineering projects. Here are some notable applications:
- Urban Planning and Construction:
In urban planning, perimeter calculations help in determining the boundaries of plots and the layout of streets and buildings. For instance, architects use perimeter measurements to design building layouts and ensure that structures fit within designated areas. In construction, knowing the perimeter of a site helps in estimating the amount of materials needed for fencing, walls, and other boundary-related structures.
- Agriculture:
Farmers and gardeners use perimeter calculations to plan the layout of fields and gardens. For example, determining the perimeter of a garden plot is essential for installing fencing to protect crops from animals. Similarly, knowing the perimeter of a field can help in calculating the amount of irrigation equipment required.
- Security:
Perimeter calculations are crucial in security planning for properties. By determining the perimeter, property owners can decide on the length of fencing or walls needed to secure the area. This is especially important for large estates, industrial complexes, and sensitive facilities where perimeter security is a priority.
- Sports:
In sports, the perimeter defines the playing area of fields, courts, and tracks. For example, the perimeter of a football field or a running track is calculated to ensure it meets the required dimensions for official competitions. Accurate perimeter measurements are essential for fair play and consistency in sports.
- Interior Design:
Interior designers use perimeter calculations to determine the length of materials needed for decorating spaces. For instance, calculating the perimeter of a room helps in estimating the amount of baseboard, crown molding, or wallpaper required for a renovation project.
- Land Surveying:
Land surveyors use perimeter calculations to measure and map out property boundaries. Accurate perimeter measurements ensure that properties are correctly defined, preventing disputes between neighbors and ensuring legal compliance in real estate transactions.
- Engineering:
Engineers use perimeter calculations in various projects, such as designing road networks, bridges, and tunnels. Knowing the perimeter helps in planning the layout and ensuring that structures are built to precise specifications.
Understanding and applying perimeter calculations is essential not only for academic purposes but also for practical applications in everyday life. From ensuring the security of properties to aiding in construction and agricultural planning, the concept of perimeter plays a vital role in numerous fields.
Urban Planning and Construction
The calculation of polygon perimeters plays a crucial role in urban planning and construction. Accurate perimeter measurements are essential for various tasks, from designing buildings to planning entire city layouts. Here’s how polygon perimeters are used in urban planning and construction:
-
Site Layout and Design
Urban planners and architects use the perimeter of building footprints to design site layouts effectively. By measuring the perimeter of a plot, they can plan the placement of buildings, parking lots, green spaces, and other infrastructure.
For example, a rectangular plot with a perimeter of \((2 \times (l + w))\) allows planners to allocate space for buildings and other facilities while ensuring efficient land use.
-
Infrastructure Planning
Infrastructure such as roads, sidewalks, and utility lines must be planned around the perimeters of existing and proposed buildings. Calculating the perimeter helps in determining the lengths of roads and the placement of utilities.
This is particularly important in densely populated urban areas where space is limited and efficient use of land is critical.
-
Resource Allocation
Knowing the perimeter of a construction site helps in estimating the amount of materials needed, such as fencing, wiring, and piping. For instance, if a construction site is enclosed by a polygonal fence, the total length of the fencing required equals the perimeter of the site.
-
Zoning and Legal Boundaries
Urban planners use perimeter calculations to define zoning boundaries and legal property lines. This ensures that land use complies with zoning regulations and helps in resolving disputes over property boundaries.
-
Environmental Considerations
Incorporating green spaces and ensuring proper drainage are essential in urban planning. Calculating the perimeter of natural features like parks and water bodies helps in planning buffer zones and drainage systems.
-
3D Modeling and Visualization
Modern urban planning often involves 3D modeling of cityscapes. Accurate perimeter data of buildings and plots is essential for creating realistic and precise 3D models. These models help in visualizing the impact of new constructions on existing urban landscapes.
For instance, using GIS tools, planners can overlay building footprints on a map to visualize the spatial relationships and optimize the urban layout.
In conclusion, the calculation of polygon perimeters is a fundamental aspect of urban planning and construction. It aids in efficient design, resource allocation, and compliance with regulations, ultimately contributing to the creation of well-organized and sustainable urban environments.
Agricultural Uses
The concept of polygon perimeter plays a crucial role in modern agricultural practices, particularly in the mapping and management of farmland. By accurately determining the perimeter of agricultural fields, farmers and agricultural planners can enhance land use efficiency, monitor crop growth, and implement sustainable farming practices.
Applications in Agriculture
- Farm Boundary Mapping: Accurate mapping of farm boundaries using polygon perimeter calculations helps in precise land measurement, ensuring optimal use of available space. This is essential for smallholder farms where every square meter counts.
- Irrigation Planning: Knowing the perimeter of a field assists in designing efficient irrigation systems. Perimeter measurements help in laying out irrigation pipes and sprinklers, ensuring even water distribution.
- Crop Monitoring: By mapping the perimeter of different crop zones within a farm, farmers can monitor the health and growth of crops more effectively. This aids in targeted application of fertilizers and pesticides, leading to better yields.
- Land Management: Polygon mapping supports sustainable land management practices by helping in the demarcation of conservation areas, buffer zones, and areas prone to erosion.
Step-by-Step Process for Perimeter Calculation
- Field Survey: Use GPS-enabled devices to walk around the boundaries of the field. Record the coordinates at each corner of the field.
- Data Input: Input the recorded coordinates into a GIS (Geographic Information System) software to create a polygon representing the field.
- Perimeter Calculation: Use the GIS software to calculate the perimeter of the polygon. This is done by summing the distances between consecutive vertices of the polygon.
- Implementation: Utilize the calculated perimeter for planning and implementing various agricultural activities such as fencing, irrigation, and crop rotation.
Example of Perimeter Calculation in Agriculture
Consider a rectangular field with lengths of 200 meters and 150 meters. The perimeter (P) is calculated using the formula for the perimeter of a rectangle:
\[ P = 2 \times ( \text{length} + \text{width} ) \]
Substituting the values:
\[ P = 2 \times (200 \, \text{m} + 150 \, \text{m}) = 2 \times 350 \, \text{m} = 700 \, \text{m} \]
This perimeter measurement can then be used to plan irrigation systems, install fences, and organize planting patterns.
Benefits of Using Polygon Perimeter in Agriculture
- Enhanced Precision: Provides accurate measurements which are critical for effective farm management.
- Resource Efficiency: Helps in the optimal use of water, fertilizers, and other resources by precise planning based on accurate field dimensions.
- Sustainability: Supports sustainable farming practices by enabling better land use planning and management.
Geometric and Engineering Applications
The calculation of polygon perimeters plays a crucial role in various geometric and engineering applications. These applications range from the design and analysis of structures to practical implementations in different fields.
Structural Engineering
In structural engineering, polygons are integral to the design of trusses used in bridges and buildings. Trusses, which often consist of triangular units, efficiently distribute loads and provide stability. Engineers analyze the perimeters of these polygons to ensure the strength and durability of the structures.
- Planar Trusses: These are two-dimensional trusses commonly used in roof supports and bicycle frames. They are designed to handle loads within a single plane.
- Space Trusses: These three-dimensional trusses, used in large structures like bridges, support loads from multiple directions. Understanding the perimeter helps in determining the length and placement of support members.
Material Optimization
Optimizing materials in construction involves calculating the perimeter of polygons to minimize waste and cost. For example:
- In sheet metal cutting, efficient use of materials depends on precisely calculating the perimeter to reduce excess cuts and scraps.
- In textile manufacturing, patterns are laid out based on polygonal shapes to ensure minimal waste of fabric.
Geometric Design
Polygons are foundational in geometric design, which is applied in creating patterns for various engineering components. For example:
- Gears: Regular polygons, such as hexagons, are used in gear design for machinery, ensuring smooth and consistent motion.
- Bolts and Screws: These components often feature polygonal heads (e.g., hexagonal) for tools to grip effectively.
Load Distribution
Understanding the perimeter of polygons helps in calculating the load distribution across different sections of a structure. For instance, in bridge engineering:
- Engineers calculate the total perimeter of truss segments to determine the amount of material needed for construction.
- They use the perimeter to assess the distribution of tension and compression forces within the truss, ensuring the bridge can handle expected loads.
Mathematical Modeling
Polygons and their perimeters are used in mathematical models to simulate real-world phenomena, which include:
- Environmental Modeling: Using polygons to represent areas of different land types for environmental impact assessments.
- Robotics: Path planning for robots often involves navigating polygonal spaces, requiring precise perimeter calculations to avoid obstacles.
Conclusion
In conclusion, the perimeter of polygons is a fundamental concept that finds extensive applications in geometric design and engineering. From optimizing materials to ensuring structural integrity and facilitating mathematical modeling, the precise calculation and understanding of polygon perimeters are essential for various technological and engineering advancements.

Tools and Techniques for Measuring Perimeter
Measuring the perimeter of a polygon is an essential task in various fields such as geometry, engineering, construction, and more. Accurate perimeter measurement requires understanding different tools and techniques, which can be categorized into manual methods and digital tools.
Manual Methods
Manual methods involve using traditional tools that require physical measurements. These methods are often used in situations where simplicity and cost-effectiveness are important.
- Ruler or Measuring Tape: For small polygons, a ruler or measuring tape can be used to measure each side. The perimeter is then calculated by summing the lengths of all sides.
- Trundle Wheel: A trundle wheel is useful for measuring longer distances. It is rolled along the sides of the polygon, and the perimeter is obtained by adding up the distances measured by the wheel.
- Caliper: For precise measurements, especially in engineering applications, calipers can be used to measure the length of each side of a polygon.
Digital Tools
Digital tools have advanced the accuracy and ease of measuring the perimeter of polygons, especially in complex applications.
- Laser Distance Measurer: A laser distance measurer can accurately measure the distance between points, making it ideal for measuring the sides of a polygon, especially in construction and surveying.
- GPS Devices: In large-scale applications like land surveying, GPS devices are used to determine the coordinates of the vertices of a polygon. The perimeter can then be calculated using the distance formula.
- Geographic Information Systems (GIS): GIS software can analyze spatial data to calculate the perimeter of polygons accurately. This is particularly useful in urban planning and environmental studies.
Step-by-Step Technique for Manual Measurement
- Identify and mark all vertices of the polygon.
- Use a measuring tape or ruler to measure the length of each side between the vertices.
- Record the measurements carefully.
- Sum all the measured lengths to obtain the total perimeter.
Using Coordinates to Calculate Perimeter
When the coordinates of the vertices of a polygon are known, the perimeter can be calculated using the distance formula:
\( \text{Perimeter} = \sum_{i=1}^{n} \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} \)
Here, \( (x_i, y_i) \) are the coordinates of the vertices, and \( n \) is the number of vertices, with \( (x_{n+1}, y_{n+1}) \) being the same as \( (x_1, y_1) \) to close the polygon.
Applications
Accurate perimeter measurements are crucial in various applications:
- Construction: Ensuring the accuracy of the boundaries of plots and structures.
- Surveying: Defining land parcels and property lines.
- Engineering: Designing components and systems with precise specifications.
Perimeter and Area: Differences and Relationships
Understanding the differences and relationships between perimeter and area is fundamental in geometry. While both concepts deal with measurements of geometric shapes, they describe different attributes.
Definitions
- Perimeter: The perimeter is the total distance around the boundary of a two-dimensional shape. It is measured in linear units (e.g., meters, feet).
- Area: The area is the amount of space occupied within the boundary of a two-dimensional shape. It is measured in square units (e.g., square meters, square feet).
Key Differences
| Basis for Comparison | Area | Perimeter |
|---|---|---|
| Meaning | Measurement of the surface of the object | Length of the boundary surrounding the shape |
| Units | Square units (e.g., m2) | Linear units (e.g., m) |
| Dimensions Involved | Two (length and width) | One (length) |
| Example | Space covered by a garden | Length of the fence around the garden |
Formulas
| Shape | Area | Perimeter |
|---|---|---|
| Square | \(a^2\) | 4a |
| Rectangle | \(l \times b\) | 2(l + b) |
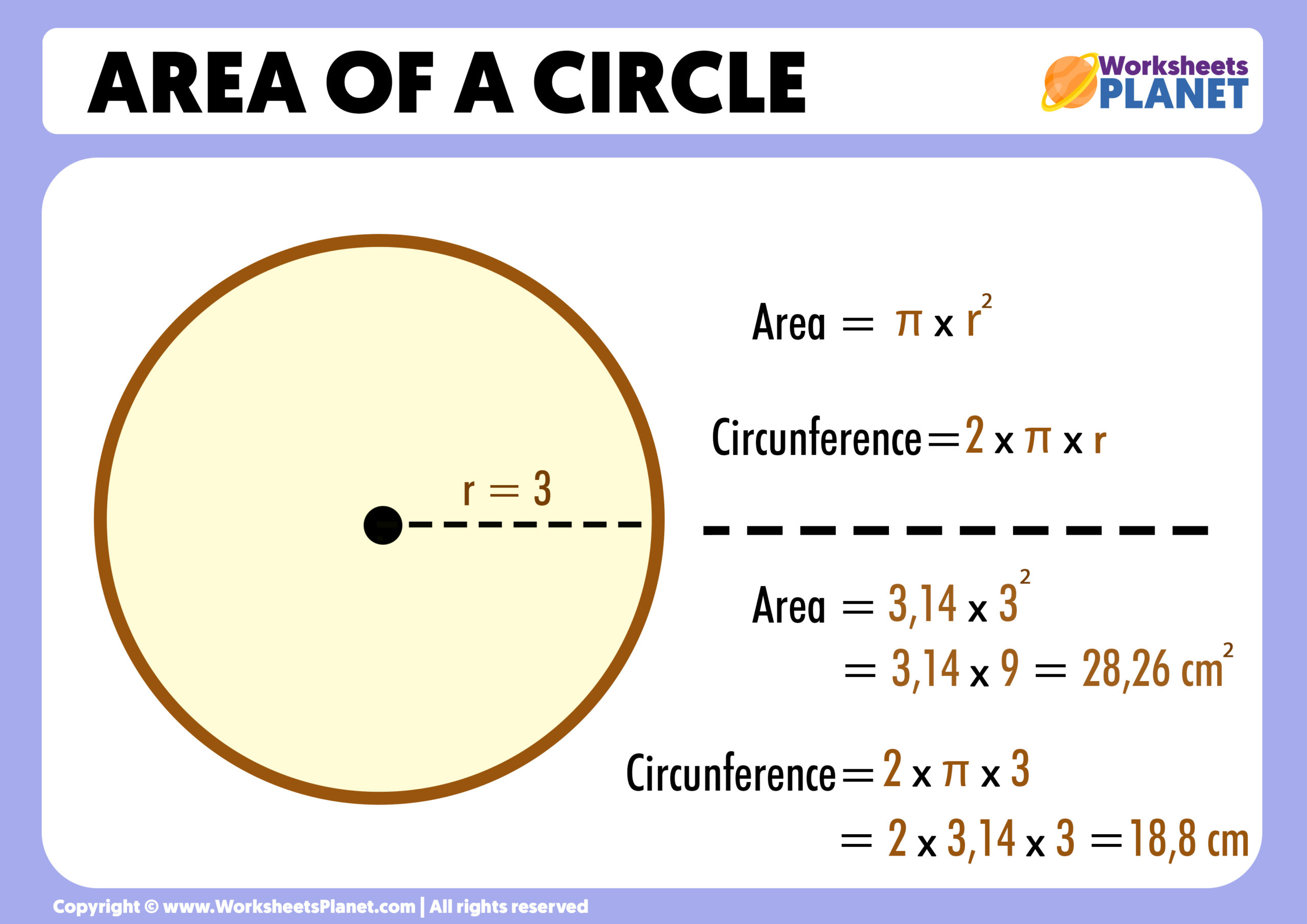
| Circle | \(\pi r^2\) | \(2\pi r\) |
| Triangle | \(\frac{1}{2}bh\) | a + b + c |
Relationship between Perimeter and Area
While perimeter and area measure different aspects of a shape, there are scenarios where understanding both is crucial:
- Shapes with the same perimeter can have different areas. For example, a square and a rectangle can have the same perimeter but different areas.
- Shapes with the same area can have different perimeters. For instance, a long, narrow rectangle can have the same area as a square but a larger perimeter.
Practical Applications
Understanding the perimeter and area is essential in various fields:
- Architecture and Construction: Calculating the perimeter is crucial for determining the length of materials needed for framing, fencing, and borders. The area is used to estimate the space for flooring, tiling, and carpeting.
- Landscaping and Agriculture: Perimeter measurements help in planning the length of fencing required. Area measurements are used to determine the space available for planting and irrigation.
Conclusion
In summary, while the perimeter and area are distinct concepts, both are integral to understanding and working with geometric shapes. Mastery of these concepts is essential for practical applications in various fields such as construction, landscaping, and design.
Cách tính chu vi đa giác
READ MORE:
Học cách tính chu vi của các đa giác một cách dễ hiểu và chi tiết, video này sẽ giúp bạn nắm vững khái niệm về chu vi của các đa giác.
Tính Chu Vi Của Các Đa Giác