Topic can perimeter be bigger than area: Discover the fascinating mathematical concept of how the perimeter can be larger than the area in certain shapes. This article delves into various examples, explanations, and real-life applications to help you understand this intriguing relationship between perimeter and area. Join us as we explore this captivating aspect of geometry.
Table of Content
- Can Perimeter Be Bigger Than Area?
- Introduction
- Understanding Perimeter and Area
- Mathematical Formulas
- Perimeter Greater Than Area: Examples
- Small Shapes and Their Properties
- Rectangles: Perimeter vs. Area
- Squares: Perimeter vs. Area
- Circles: Perimeter vs. Area
- Comparison of Different Shapes
- Impact of Dimensions on Perimeter and Area
- Special Cases in Geometry
- Applications in Real Life
- Frequently Asked Questions
- YOUTUBE:
Can Perimeter Be Bigger Than Area?
The relationship between the perimeter and the area of a shape is an interesting mathematical concept. For certain shapes, the perimeter can indeed be greater than the area. Here are some examples and explanations:
Rectangles
For rectangles, the perimeter can be calculated as:
\[\text{Perimeter} = 2(l + w)\]
And the area is:
\[\text{Area} = l \times w\]
Consider a rectangle with length \( l = 1 \) and width \( w = 1 \):
- Perimeter: \( 2(1 + 1) = 4 \)
- Area: \( 1 \times 1 = 1 \)
In this case, the perimeter (4) is greater than the area (1).
Circles
For circles, the circumference (perimeter) and area are given by:
\[\text{Circumference} = 2 \pi r\]
\[\text{Area} = \pi r^2\]
For a circle with a very small radius, \( r \), the circumference can be larger than the area. For instance, if \( r = 0.5 \):
- Circumference: \( 2 \pi (0.5) = \pi \approx 3.14 \)
- Area: \( \pi (0.5)^2 = \pi \times 0.25 \approx 0.785 \)
Here, the circumference (approximately 3.14) is greater than the area (approximately 0.785).
Squares
For squares, the perimeter and area are given by:
\[\text{Perimeter} = 4s\]
\[\text{Area} = s^2\]
For a square with side length \( s = 1 \):
- Perimeter: \( 4 \times 1 = 4 \)
- Area: \( 1^2 = 1 \)
Thus, the perimeter (4) is greater than the area (1).
General Observation
In general, for shapes with small dimensions, the perimeter often exceeds the area. As the size of the shape increases, the area grows faster than the perimeter. This is because the area is a function of the square of the dimensions, while the perimeter is a linear function.
Conclusion
It is indeed possible for the perimeter of a shape to be greater than its area, especially in cases of shapes with smaller dimensions. The relationship varies depending on the type and size of the shape.
READ MORE:
Introduction
Understanding the relationship between perimeter and area is a fundamental aspect of geometry. This intriguing concept often raises the question: Can the perimeter of a shape be larger than its area? The answer is yes, and this article explores how and why this happens through various examples and mathematical explanations.
Let's start by defining perimeter and area:
- Perimeter: The total distance around the edge of a two-dimensional shape.
- Area: The amount of space enclosed within the boundaries of a two-dimensional shape.
To comprehend how the perimeter can exceed the area, consider small shapes where this phenomenon is more evident. For instance, let's take a look at squares and rectangles with minimal dimensions:
- Square with side length 1:
- Perimeter: \(4 \times 1 = 4\)
- Area: \(1^2 = 1\)
- Rectangle with length 2 and width 0.5:
- Perimeter: \(2(2 + 0.5) = 5\)
- Area: \(2 \times 0.5 = 1\)
From these examples, it's clear that the perimeter can indeed be greater than the area, especially in smaller shapes. As shapes increase in size, their areas tend to grow faster than their perimeters due to the square relationship of the area formula compared to the linear relationship of the perimeter.
This concept is not just limited to basic shapes but extends to more complex geometries as well. By exploring various shapes and their dimensions, one can gain a deeper understanding of how perimeter and area interact.
In the following sections, we will delve deeper into specific examples, mathematical proofs, and real-life applications to illustrate this fascinating relationship.
Understanding Perimeter and Area
To explore how the perimeter can be larger than the area, it's essential to first understand the definitions and formulas for perimeter and area.
Perimeter is the total distance around the edge of a two-dimensional shape. It is a linear measurement. The formulas for the perimeter of common shapes are:
- Rectangle: \(P = 2(l + w)\)
- Square: \(P = 4s\)
- Circle (Circumference): \(P = 2\pi r\)
Area is the amount of space enclosed within the boundaries of a two-dimensional shape. It is measured in square units. The formulas for the area of common shapes are:
- Rectangle: \(A = l \times w\)
- Square: \(A = s^2\)
- Circle: \(A = \pi r^2\)
To illustrate how the perimeter can be greater than the area, consider the following examples:
- Square with side length 1:
- Perimeter: \(4 \times 1 = 4\)
- Area: \(1^2 = 1\)
- Rectangle with length 2 and width 0.5:
- Perimeter: \(2(2 + 0.5) = 5\)
- Area: \(2 \times 0.5 = 1\)
- Circle with radius 0.5:
- Perimeter (Circumference): \(2 \pi \times 0.5 \approx 3.14\)
- Area: \(\pi \times (0.5)^2 \approx 0.785\)
These examples demonstrate that for smaller shapes, the perimeter can indeed exceed the area. This is particularly noticeable in shapes with smaller dimensions, where the linear measurement of the perimeter grows faster relative to the square measurement of the area.
As shapes increase in size, their areas tend to grow more quickly than their perimeters due to the square relationship of area formulas compared to the linear relationship of perimeter formulas. This fundamental understanding of perimeter and area lays the groundwork for further exploration of their mathematical relationship.
Mathematical Formulas
Understanding the mathematical formulas for perimeter and area is crucial to comprehending how the perimeter can be greater than the area in certain cases. Below are the formulas for common shapes:
- Rectangle
- Perimeter: \(P = 2(l + w)\)
- Area: \(A = l \times w\)
- Square
- Perimeter: \(P = 4s\)
- Area: \(A = s^2\)
- Circle
- Perimeter (Circumference): \(P = 2\pi r\)
- Area: \(A = \pi r^2\)
To see how the perimeter can be larger than the area, let's calculate these values for shapes with small dimensions:
- Square with side length 1
- Perimeter: \(P = 4 \times 1 = 4\)
- Area: \(A = 1^2 = 1\)
- Rectangle with length 2 and width 0.5
- Perimeter: \(P = 2(2 + 0.5) = 5\)
- Area: \(A = 2 \times 0.5 = 1\)
- Circle with radius 0.5
- Perimeter (Circumference): \(P = 2 \pi \times 0.5 \approx 3.14\)
- Area: \(A = \pi \times (0.5)^2 \approx 0.785\)
These calculations demonstrate that for smaller shapes, the perimeter can exceed the area. This occurs because the formulas for perimeter and area scale differently as the dimensions of the shapes change.
In general, the perimeter is a linear function of the dimensions, while the area is a quadratic function. As the dimensions increase, the area grows faster than the perimeter, but for small dimensions, the perimeter can be greater.
Understanding these mathematical relationships helps to clarify why and when the perimeter can be larger than the area, providing a solid foundation for exploring more complex shapes and real-life applications.
Perimeter Greater Than Area: Examples
Examining specific examples helps to understand how the perimeter of a shape can be greater than its area. Here are a few detailed examples demonstrating this concept:
- Square with Side Length 1
- Perimeter: \(P = 4 \times 1 = 4\)
- Area: \(A = 1^2 = 1\)
In this case, the perimeter (4) is greater than the area (1).
- Rectangle with Length 2 and Width 0.5
- Perimeter: \(P = 2(2 + 0.5) = 5\)
- Area: \(A = 2 \times 0.5 = 1\)
Here, the perimeter (5) is greater than the area (1).
- Circle with Radius 0.5
- Perimeter (Circumference): \(P = 2 \pi \times 0.5 \approx 3.14\)
- Area: \(A = \pi \times (0.5)^2 \approx 0.785\)
In this example, the perimeter (approximately 3.14) is greater than the area (approximately 0.785).
These examples clearly show that for shapes with smaller dimensions, the perimeter can exceed the area. This is particularly evident in shapes with minimal side lengths or radii.
To further illustrate, let's consider another set of examples with slightly different dimensions:
- Rectangle with Length 1 and Width 0.1
- Perimeter: \(P = 2(1 + 0.1) = 2.2\)
- Area: \(A = 1 \times 0.1 = 0.1\)
Here, the perimeter (2.2) is much greater than the area (0.1).
- Circle with Radius 0.1
- Perimeter (Circumference): \(P = 2 \pi \times 0.1 \approx 0.628\)
- Area: \(A = \pi \times (0.1)^2 \approx 0.0314\)
In this case, the perimeter (approximately 0.628) is significantly greater than the area (approximately 0.0314).
From these calculations, it's evident that the relationship between perimeter and area varies with the size of the shape. As dimensions increase, the area grows more rapidly than the perimeter. However, for small dimensions, the perimeter can indeed be greater than the area, providing an interesting insight into geometric properties.

Small Shapes and Their Properties
Small shapes often exhibit the interesting property where their perimeter can be greater than their area. This phenomenon is primarily due to the way perimeter and area are calculated and how they scale with the dimensions of the shape. Here, we will examine various small shapes to understand this relationship better.
- Square with Side Length 0.5
- Perimeter: \(P = 4 \times 0.5 = 2\)
- Area: \(A = 0.5^2 = 0.25\)
In this example, the perimeter (2) is significantly greater than the area (0.25).
- Rectangle with Length 1 and Width 0.2
- Perimeter: \(P = 2(1 + 0.2) = 2.4\)
- Area: \(A = 1 \times 0.2 = 0.2\)
Here, the perimeter (2.4) is much greater than the area (0.2).
- Circle with Radius 0.1
- Perimeter (Circumference): \(P = 2 \pi \times 0.1 \approx 0.628\)
- Area: \(A = \pi \times (0.1)^2 \approx 0.0314\)
In this case, the perimeter (approximately 0.628) is significantly greater than the area (approximately 0.0314).
- Triangle with Base 1 and Height 0.1 (assuming an isosceles triangle)
- Perimeter: \(P = 2\sqrt{\left(\frac{1}{2}\right)^2 + 0.1^2} + 1 \approx 2.02\)
- Area: \(A = \frac{1 \times 0.1}{2} = 0.05\)
Here, the perimeter (approximately 2.02) is much greater than the area (0.05).
These examples clearly illustrate that for small shapes, the perimeter can exceed the area. This is because the perimeter is a linear measure, while the area is a measure of two dimensions (length squared). As shapes increase in size, the area tends to grow faster than the perimeter. However, with very small dimensions, the linear growth of the perimeter surpasses the quadratic growth of the area.
Understanding the properties of small shapes helps to grasp the fundamental principles of geometry and the relationship between different geometric measures. This insight can be particularly useful in various fields, such as design, architecture, and even nature studies, where the size and shape of objects play a crucial role.
Rectangles: Perimeter vs. Area
The relationship between the perimeter and area of rectangles is a fascinating aspect of geometry. By examining various rectangles, we can understand how their perimeters can sometimes exceed their areas, particularly when the dimensions are small.
For a rectangle, the formulas for perimeter and area are:
- Perimeter: \(P = 2(l + w)\)
- Area: \(A = l \times w\)
Let's analyze some examples to see this relationship in action:
- Rectangle with Length 2 and Width 0.5
- Perimeter: \(P = 2(2 + 0.5) = 5\)
- Area: \(A = 2 \times 0.5 = 1\)
Here, the perimeter (5) is greater than the area (1).
- Rectangle with Length 1 and Width 0.1
- Perimeter: \(P = 2(1 + 0.1) = 2.2\)
- Area: \(A = 1 \times 0.1 = 0.1\)
In this case, the perimeter (2.2) is significantly greater than the area (0.1).
- Rectangle with Length 3 and Width 0.2
- Perimeter: \(P = 2(3 + 0.2) = 6.4\)
- Area: \(A = 3 \times 0.2 = 0.6\)
Here, the perimeter (6.4) is much greater than the area (0.6).
These examples demonstrate that for rectangles with small dimensions, the perimeter can exceed the area. This is due to the linear nature of the perimeter formula, which scales with the sum of the length and width, while the area formula scales with the product of the length and width.
To understand this relationship further, consider a general rectangle with length \(l\) and width \(w\). For the perimeter to be greater than the area, the following inequality must hold:
\[ 2(l + w) > l \times w \]
Rearranging this inequality, we get:
\[ 2l + 2w > lw \]
\[ lw - 2l - 2w < 0 \]
\[ l(w - 2) < 2w \]
This inequality shows that when both \(l\) and \(w\) are small, the perimeter can indeed be greater than the area. However, as the dimensions increase, the area starts to grow faster than the perimeter, reversing this relationship.
By exploring various dimensions of rectangles, we gain a deeper understanding of how perimeter and area interact, providing valuable insights into geometric properties and their applications in real-world scenarios.
Squares: Perimeter vs. Area
Squares are a unique type of rectangle where all sides are equal in length. This simplicity allows for a straightforward examination of the relationship between perimeter and area. By exploring various side lengths, we can see how the perimeter can sometimes be greater than the area, particularly for smaller squares.
For a square, the formulas for perimeter and area are:
- Perimeter: \(P = 4s\)
- Area: \(A = s^2\)
Let's analyze some examples to understand this relationship better:
- Square with Side Length 1
- Perimeter: \(P = 4 \times 1 = 4\)
- Area: \(A = 1^2 = 1\)
Here, the perimeter (4) is greater than the area (1).
- Square with Side Length 0.5
- Perimeter: \(P = 4 \times 0.5 = 2\)
- Area: \(A = 0.5^2 = 0.25\)
In this case, the perimeter (2) is significantly greater than the area (0.25).
- Square with Side Length 0.2
- Perimeter: \(P = 4 \times 0.2 = 0.8\)
- Area: \(A = 0.2^2 = 0.04\)
Here, the perimeter (0.8) is much greater than the area (0.04).
These examples show that for squares with smaller side lengths, the perimeter can exceed the area. This occurs because the perimeter is a linear measurement (multiplying the side length by 4), while the area is a quadratic measurement (squaring the side length).
To further understand this relationship, consider a general square with side length \(s\). For the perimeter to be greater than the area, the following inequality must hold:
\[ 4s > s^2 \]
Rearranging this inequality, we get:
\[ s^2 - 4s < 0 \]
\[ s(s - 4) < 0 \]
This inequality is satisfied when \(0 < s < 4\). Thus, for any square with a side length less than 4 units, the perimeter will be greater than the area.
This analysis illustrates the unique properties of squares and how their perimeter can surpass their area when the side lengths are small. As the side length increases beyond 4 units, the area grows faster than the perimeter, reversing this relationship. Understanding these principles helps to deepen our knowledge of geometric properties and their practical implications.
Circles: Perimeter vs. Area
In geometry, the concepts of perimeter and area are crucial in understanding the properties of different shapes. For circles, these concepts are particularly interesting because of the relationship between the circumference (perimeter) and the area. Let's delve into how the perimeter of a circle can compare to its area.
The perimeter of a circle, also known as the circumference, is given by the formula:
Where:
- C is the circumference
- π (pi) is approximately 3.14159
- r is the radius of the circle
The area of a circle is given by the formula:
Where:
- A is the area
- π (pi) is approximately 3.14159
- r is the radius of the circle
To understand when the circumference is greater than the area, let's compare the formulas directly:
If (circumference) is greater than (area), we have:
By simplifying this inequality, we divide both sides by :
Dividing both sides by (assuming ):
This shows that the circumference of a circle is greater than its area when the radius is less than 2 units. Hence, for small circles with a radius less than 2 units, the perimeter can indeed be larger than the area.
Let's look at a few examples:
| Radius (r) | Circumference (C) | Area (A) | C > A? |
|---|---|---|---|
| 1 | 6.28 | 3.14 | Yes |
| 1.5 | 9.42 | 7.07 | Yes |
| 2 | 12.57 | 12.57 | Equal |
| 2.5 | 15.71 | 19.63 | No |
In conclusion, while it might seem counterintuitive at first, the perimeter of a circle can be larger than its area for smaller radii. As the radius increases, the area grows faster than the circumference, leading to a situation where the area becomes larger than the perimeter.
Comparison of Different Shapes
When comparing the perimeter and area of different shapes, it's important to understand how these measurements vary with changes in dimensions. Different shapes exhibit unique relationships between their perimeter and area, which can lead to interesting observations, especially for smaller shapes.
Let's consider some common shapes: squares, rectangles, and circles. We will compare their perimeters and areas to see when the perimeter can be larger than the area.
Squares
For a square, both the perimeter and area can be calculated as follows:
- Perimeter (P):
- Area (A):
To determine when the perimeter is greater than the area:
Dividing both sides by :
This shows that the perimeter is greater than the area when the side length is less than 4 units.
Rectangles
For a rectangle, the perimeter and area are given by:
- Perimeter (P):
- Area (A):
To compare the perimeter and area, let's consider some example dimensions:
| Length (l) | Width (w) | Perimeter (P) | Area (A) | P > A? |
|---|---|---|---|---|
| 2 | 1 | 6 | 2 | Yes |
| 3 | 1 | 8 | 3 | Yes |
| 3 | 2 | 10 | 6 | Yes |
| 4 | 3 | 14 | 12 | Yes |
| 4 | 4 | 16 | 16 | Equal |
| 5 | 4 | 18 | 20 | No |
Circles
For circles, we use the formulas for circumference and area:
- Circumference (C):
- Area (A):
We compare the two as follows:
If > , then
Which simplifies to:
Thus, for a circle, the circumference is greater than the area when the radius is less than 2 units.
Triangles
Triangles can be more complex, but for simplicity, let's consider equilateral triangles. The perimeter and area formulas are:
- Perimeter (P):
- Area (A):
Comparing these values requires more complex algebra, but it can be observed that for small side lengths, the perimeter can be larger than the area.
In conclusion, while the relationship between perimeter and area varies across different shapes, smaller dimensions tend to result in the perimeter being larger than the area. This understanding helps in various fields, including architecture, design, and everyday problem-solving.
Impact of Dimensions on Perimeter and Area
The relationship between perimeter and area is significantly influenced by the dimensions of a shape. Understanding this relationship helps in various applications, from geometry to real-life scenarios. Here, we explore how changes in dimensions impact both perimeter and area for different shapes.
Squares
For a square with side length :
- Perimeter (P):
- Area (A):
As increases, the area grows faster than the perimeter. For example, a square with side length 1 has a perimeter of 4 and an area of 1, but a square with side length 10 has a perimeter of 40 and an area of 100.
Rectangles
For a rectangle with length and width :
- Perimeter (P):
- Area (A):
Changing the dimensions affects both the perimeter and area. For instance, a rectangle with dimensions 2 by 1 has a perimeter of 6 and an area of 2, whereas a rectangle with dimensions 20 by 10 has a perimeter of 60 and an area of 200.
Circles
For a circle with radius :
- Circumference (C):
- Area (A):
As the radius increases, the area increases much faster than the circumference. For example, a circle with radius 1 has a circumference of approximately 6.28 and an area of approximately 3.14. A circle with radius 10 has a circumference of approximately 62.8 and an area of approximately 314.
Triangles
Consider an equilateral triangle with side length :
- Perimeter (P):
- Area (A):
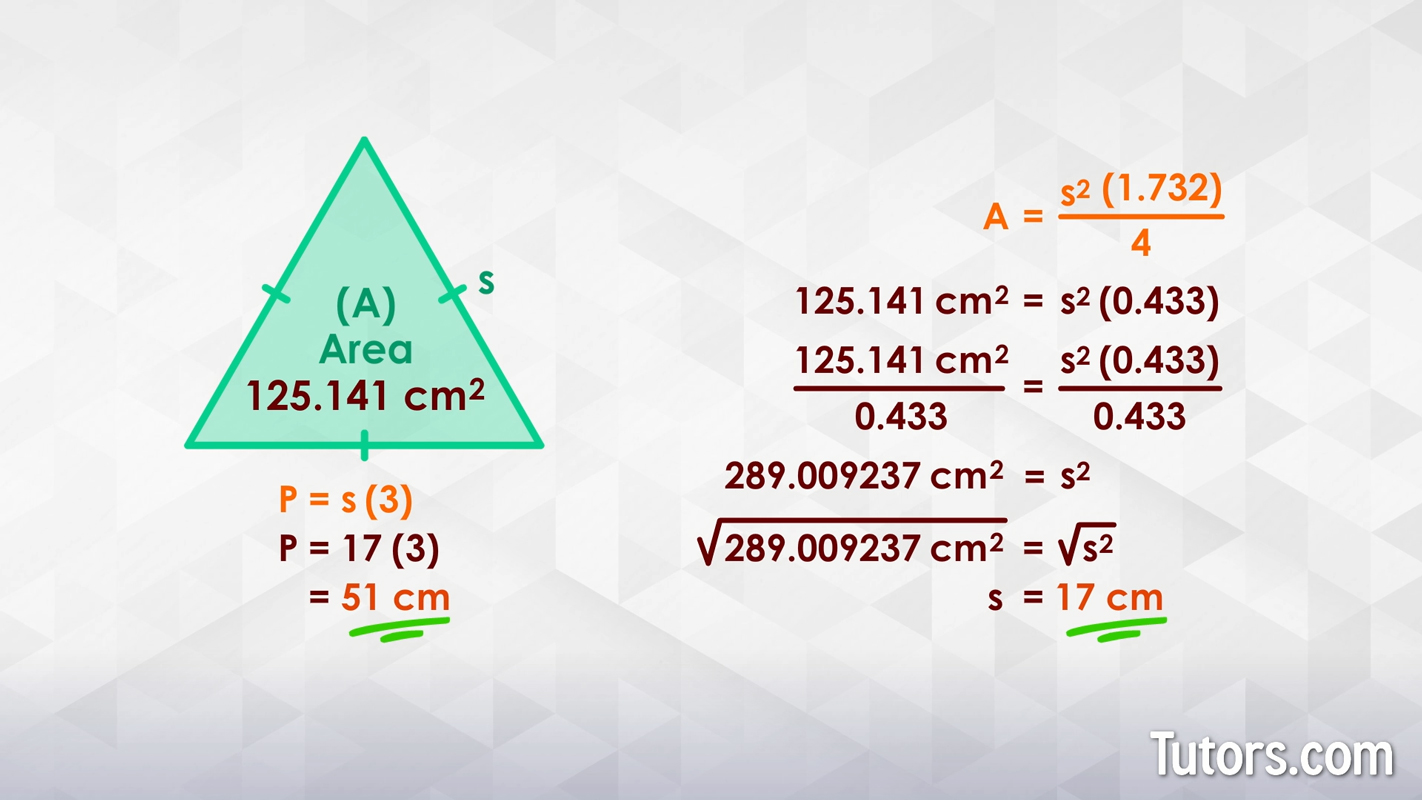
For small side lengths, the perimeter can be larger than the area. For example, a triangle with side length 1 has a perimeter of 3 and an area of approximately 0.433. As the side length increases, the area grows faster. A triangle with side length 10 has a perimeter of 30 and an area of approximately 43.3.
To summarize, the impact of dimensions on perimeter and area varies across different shapes. Generally, for smaller dimensions, the perimeter can be larger than the area. As dimensions increase, the area tends to grow faster than the perimeter, reflecting the geometric properties of each shape.
Special Cases in Geometry
In geometry, certain shapes and configurations present special cases where the perimeter can be greater than the area. Understanding these cases helps in grasping the nuances of geometric properties and their applications. Here, we explore some of these special cases step by step.
1. Small Equilateral Triangles
For an equilateral triangle with side length :
- Perimeter (P):
- Area (A):
For small side lengths, the perimeter can be larger than the area. For example, when , the perimeter is 3 and the area is approximately 0.433.
2. Very Small Rectangles
Consider a rectangle with length and width :
- Perimeter (P):
- Area (A):
If both and are small, the perimeter can exceed the area. For example, a rectangle with dimensions 1 by 0.5 has a perimeter of 3 and an area of 0.5.
3. Thin and Long Rectangles
For a rectangle where one side is much longer than the other, the perimeter can also be greater than the area. Let's take a rectangle with length 10 and width 0.1:
- Perimeter (P): = 20.2
- Area (A): = 1
In this case, the perimeter (20.2) is much greater than the area (1).
4. Small Circles
For a circle with radius :
- Circumference (C):
- Area (A):
When the radius is small, the circumference can be greater than the area. For instance, with a radius of 1:
- Circumference:
- Area:
Here, the circumference (6.28) is greater than the area (3.14).
5. Very Thin Shapes
Shapes with extremely small width compared to their length, such as a line segment or a very thin rectangle, often have a perimeter that is significantly greater than their area.
Consider a rectangle with length 100 and width 0.01:
- Perimeter (P): = 200.02
- Area (A): = 1
In this example, the perimeter (200.02) is much greater than the area (1).
These special cases illustrate that under certain conditions, particularly with small dimensions or extreme aspect ratios, the perimeter of a shape can indeed be larger than its area. This concept is useful in understanding geometric properties and their practical applications.
Applications in Real Life
Understanding the relationship between perimeter and area is not only a theoretical exercise but also has practical applications in various real-life scenarios. Here, we explore how these concepts are applied in different fields and everyday situations.
1. Urban Planning and Architecture
In urban planning and architecture, the design of buildings, parks, and other structures often requires careful consideration of perimeter and area:
- Fencing and Boundaries: When planning to enclose an area, such as a park or a property, knowing the perimeter is crucial for determining the length of fencing required. For smaller areas, the perimeter can be significantly larger than the area, influencing material costs.
- Space Utilization: Architects must maximize the use of available space. For small rooms or plots, the area might be small, but the perimeter is large, affecting design decisions for walls and walkways.
2. Agriculture and Landscaping
Farmers and landscapers often need to calculate the perimeter and area of fields and gardens:
- Crop Planning: The layout of crops can depend on the perimeter of the field. For example, perimeter measurements are used to plan irrigation systems that go around the edges of the fields.
- Garden Design: In designing a garden, the area is important for planting, while the perimeter is crucial for placing borders and pathways.
3. Packaging and Material Optimization
In manufacturing and packaging industries, optimizing material usage is essential:
- Packaging Design: When designing packaging for products, the surface area (perimeter) is considered to minimize material use while protecting the product. For small items, packaging might have a larger perimeter compared to the area.
- Material Cutting: In industries that cut materials into shapes, such as textiles or metalworking, knowing the relationship between perimeter and area helps in minimizing waste and maximizing efficiency.
4. Cost Estimation and Budgeting
In various projects, understanding the perimeter and area can impact cost estimation:
- Construction Projects: Estimating the cost of materials like tiles, paint, or flooring often requires knowledge of the area. However, for materials like baseboards or trim, the perimeter is more relevant.
- Event Planning: For events held in tents or temporary structures, knowing the perimeter helps in planning the setup and layout, while the area determines the capacity and space utilization.
5. Sports and Recreation
In sports, the design and maintenance of fields and courts consider both perimeter and area:
- Track and Field: The perimeter of running tracks is crucial for determining race lengths, while the area within the track is used for events like long jump or shot put.
- Playing Fields: The dimensions of soccer fields, basketball courts, and other playing surfaces require precise calculations of both perimeter and area to meet regulations and provide optimal playing conditions.
These examples illustrate how the concepts of perimeter and area are intertwined with practical considerations in various fields. By understanding these relationships, professionals can make informed decisions that optimize space, materials, and costs.

Frequently Asked Questions
Here are some commonly asked questions regarding the relationship between perimeter and area, along with detailed answers to help clarify these concepts.
1. Can the perimeter of a shape be larger than its area?
Yes, the perimeter of a shape can be larger than its area, especially in cases where the dimensions of the shape are small. For instance, a square with a side length of 1 unit has a perimeter of 4 units and an area of 1 square unit, making the perimeter larger than the area.
2. Under what conditions does the perimeter exceed the area?
The perimeter tends to exceed the area when the shape's dimensions are small or when the shape is elongated. For example, in rectangles, a very long and narrow shape can have a perimeter that is significantly larger than its area. Similarly, in circles, a small radius results in a larger circumference compared to the area.
3. How do you calculate the perimeter and area of common shapes?
The formulas for calculating the perimeter and area of common shapes are as follows:
- Square:
- Perimeter (P):
- Area (A):
- Rectangle:
- Perimeter (P):
- Area (A):
- Circle:
- Circumference (C):
- Area (A):
- Equilateral Triangle:
- Perimeter (P):
- Area (A):
4. Why is it important to understand the relationship between perimeter and area?
Understanding the relationship between perimeter and area is important for various practical applications. It helps in optimizing designs, planning efficient use of materials, and solving real-world problems in fields such as architecture, agriculture, packaging, and more. For example, knowing that a smaller area might have a larger perimeter can influence decisions on fencing, irrigation, or material usage.
5. Are there any real-life examples where the perimeter is greater than the area?
Yes, there are many real-life examples where the perimeter is greater than the area. For instance:
- A garden bed that is 1 meter by 0.5 meters has a perimeter of 3 meters and an area of 0.5 square meters.
- A circular table with a radius of 1 meter has a circumference of approximately 6.28 meters and an area of approximately 3.14 square meters.
- An athletic track designed with a very narrow width compared to its length can also have a perimeter that exceeds its area.
6. How can this knowledge be applied in everyday situations?
This knowledge can be applied in various everyday situations, such as:
- Home Improvement: Calculating the amount of trim needed for rooms (perimeter) and the paint required for walls (area).
- Gardening: Planning the layout of garden beds and pathways, where the perimeter influences the amount of edging material needed.
- Event Planning: Setting up temporary structures where the perimeter determines the length of the material for enclosures, and the area determines the space available for activities.
By understanding how perimeter and area relate to each other, we can make more informed and efficient decisions in a wide range of contexts.
Cùng Chu Vi, Diện Tích Khác Nhau. Lớp 3
Cách Tìm Chiều Dài & Chiều Rộng Khi Biết Chu Vi & Diện Tích Vuông: Kỹ Năng Toán Học