Topic is the square root of 50 rational or irrational: The square root of 50 is a fascinating topic that delves into the realm of rational and irrational numbers. In this article, we explore whether the square root of 50 is rational or irrational, providing clear definitions, mathematical proofs, and real-life applications to enhance your understanding of these intriguing mathematical concepts.
Table of Content
- Is the Square Root of 50 Rational or Irrational?
- Introduction to Rational and Irrational Numbers
- Definition of Rational Numbers
- Definition of Irrational Numbers
- Understanding Square Roots
- Simplification of the Square Root of 50
- Mathematical Proof of Irrationality
- Examples of Rational and Irrational Numbers
- Historical Context of Irrational Numbers
- Applications of Irrational Numbers in Real Life
- YOUTUBE: Video này giải thích lý do tại sao căn bậc hai của 50 là một số vô tỷ, với các ví dụ và chứng minh toán học.
Is the Square Root of 50 Rational or Irrational?
The square root of 50 is a number that, when multiplied by itself, equals 50. To determine if this number is rational or irrational, we must understand the definitions of rational and irrational numbers.
Rational Numbers
A rational number is any number that can be expressed as the quotient or fraction a/b of two integers, where a and b are integers and b is not zero. Examples of rational numbers include 1/2, 3, and -4/5.
Irrational Numbers
An irrational number cannot be expressed as a simple fraction; it cannot be written as the ratio of two integers. Examples of irrational numbers include \(\sqrt{2}\), \(\pi\), and e.
Determining the Nature of \(\sqrt{50}\)
The square root of 50 can be simplified as follows:
\[
\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}
\]
Since \(\sqrt{2}\) is known to be an irrational number, multiplying it by 5 (a rational number) still results in an irrational number.
Conclusion
Therefore, \(\sqrt{50}\) is an irrational number.
READ MORE:
Introduction to Rational and Irrational Numbers
Rational and irrational numbers are fundamental concepts in mathematics that help us understand the nature of numbers. Below, we will explore these concepts in detail.
Rational Numbers
Rational numbers are numbers that can be expressed as the quotient or fraction of two integers, where the numerator is an integer and the denominator is a non-zero integer.
- Examples: , ,
Irrational Numbers
Irrational numbers cannot be expressed as a simple fraction; their decimal form is non-repeating and non-terminating.
- Examples: , ,
Comparing Rational and Irrational Numbers
Let's compare the properties of rational and irrational numbers in the table below:
| Property | Rational Numbers | Irrational Numbers |
|---|---|---|
| Representation | Fraction of two integers | Cannot be expressed as a fraction |
| Decimal Form | Repeating or terminating | Non-repeating, non-terminating |
| Examples | , | , |
Understanding the difference between rational and irrational numbers is crucial for exploring more advanced mathematical concepts, such as the nature of square roots.
Definition of Rational Numbers
Rational numbers are a core concept in mathematics, and understanding them is essential for exploring various mathematical principles.
A rational number is any number that can be expressed as the quotient or fraction of two integers, where the numerator is an integer and the denominator is a non-zero integer. This can be written as:
, where
Characteristics of Rational Numbers
- Rational numbers can be positive, negative, or zero.
- The decimal representation of rational numbers either terminates or repeats periodically.
- They include fractions such as , integers like , and repeating decimals such as
Examples of Rational Numbers
| Example | Fraction Form | Decimal Form |
|---|---|---|
| One Half | 0.5 | |
| Three | 3.0 | |
| Negative Two Fifths | -0.4 | |
| One Third | 0.333... |
Rational numbers play a crucial role in various fields such as algebra, number theory, and real-world applications. Understanding their properties helps in comprehending more complex mathematical concepts and operations.
Definition of Irrational Numbers
Irrational numbers are an important part of the number system, providing a deeper understanding of the continuum of numbers.
An irrational number is a number that cannot be expressed as a simple fraction; in other words, it cannot be written as , where
Characteristics of Irrational Numbers
- Irrational numbers cannot be written as exact fractions.
- Their decimal expansions go on forever without repeating.
- They are not the result of dividing two integers.
Examples of Irrational Numbers
- The square root of non-perfect squares: , ,
- Mathematical constants: (pi), (Euler's number)
Comparing Irrational and Rational Numbers
The differences between rational and irrational numbers are summarized in the table below:
| Property | Rational Numbers | Irrational Numbers |
|---|---|---|
| Representation | Fraction of two integers | Cannot be expressed as a fraction |
| Decimal Form | Repeating or terminating | Non-repeating, non-terminating |
| Examples | , | , |
Understanding irrational numbers expands our comprehension of the number line and the various types of numbers that exist within it, showcasing the richness and diversity of mathematical concepts.
Understanding Square Roots
The concept of square roots is fundamental in mathematics, especially in algebra and geometry. The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical symbol .
Definition of Square Roots
If = , then is a square root of . Every positive number has two square roots: and .
Properties of Square Roots
- Non-negative Results: The principal square root of a non-negative number is always non-negative.
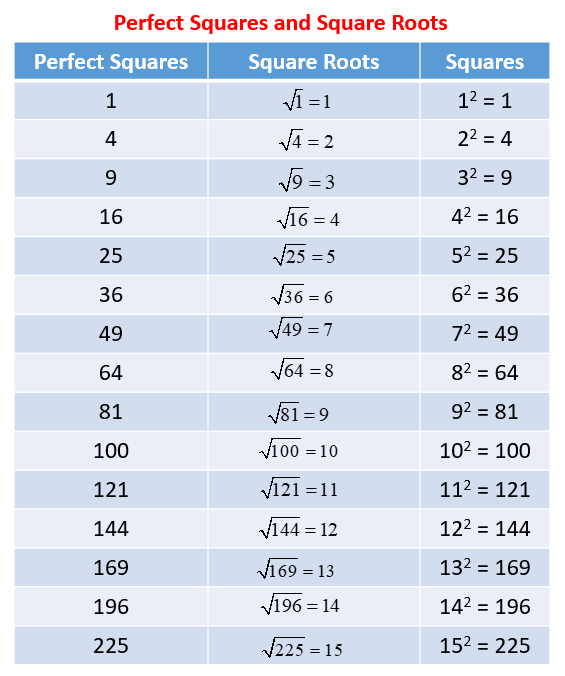
- Square Root of Perfect Squares: The square root of a perfect square is an integer. For example, = 7.
- Square Root of Non-Perfect Squares: The square root of a non-perfect square is an irrational number. For example, is irrational.
Calculating Square Roots
To calculate the square root of a number, we can use various methods such as:
- Prime factorization (for perfect squares).
- Approximation methods (for non-perfect squares).
- Using a calculator for quick and accurate results.
Examples of Square Roots
| Number | Square Root | Type |
|---|---|---|
| 16 | = 4 | Rational |
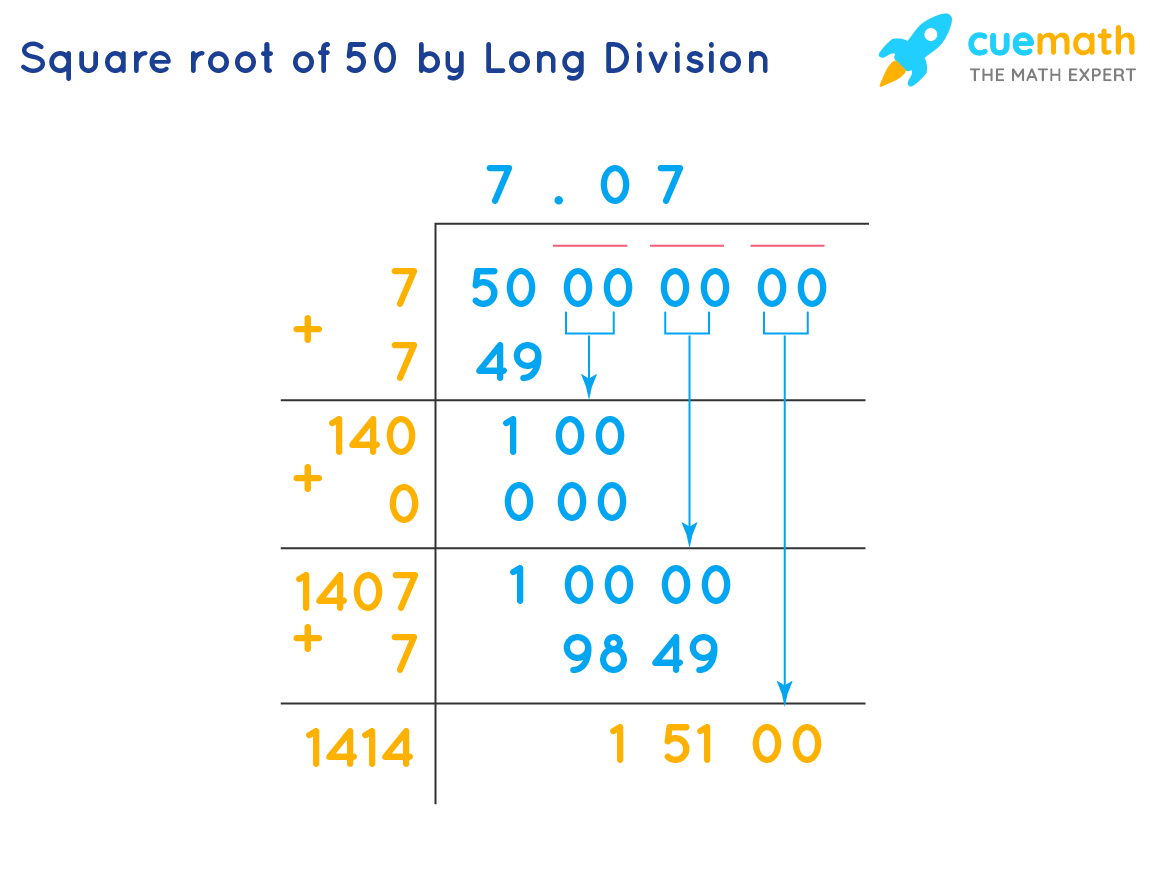
| 50 | ≈ 7.071 | Irrational |
| 81 | = 9 | Rational |
Understanding square roots is crucial for solving quadratic equations, analyzing geometric shapes, and in various real-world applications. The square root of 50, being a non-perfect square, serves as an excellent example of an irrational number.

Simplification of the Square Root of 50
Simplifying the square root of 50 involves expressing it in its simplest radical form. This process helps in understanding the properties of the number and its relation to other numbers.
Step-by-Step Simplification
- Start with the square root expression: .
- Factorize the number inside the square root. The prime factorization of 50 is: .
- Rewrite the square root using the prime factors: .
- Separate the square root into the product of square roots: .
- Simplify the square root of the perfect square: .
- Combine the simplified terms: .
- Thus, the simplified form of the square root of 50 is: .
Visual Representation
Let's look at a visual representation of this simplification:
| Expression | Simplification Steps |
|---|---|
| Original Expression | |
| Factorize 50 | |
| Separate into Product of Square Roots | |
| Simplify Perfect Square |
The square root of 50 simplifies to , showing that it is an irrational number. Understanding this simplification is crucial for various mathematical applications, including solving equations and analyzing geometric shapes.
Mathematical Proof of Irrationality
To prove that the square root of 50 is irrational, we can use a proof by contradiction. This method involves assuming the opposite of what we want to prove and then showing that this assumption leads to a contradiction.
Step-by-Step Proof
- Assume that is a rational number. This means it can be expressed as a fraction of two integers in simplest form: , where
p andq are coprime integers (having no common factors other than 1) andq ≠ 0. - According to our assumption, we have: .
- Squaring both sides, we get: .
- This can be rewritten as: .
- From this equation, we see that is divisible by 50, meaning must be divisible by both 2 and 5 (the prime factors of 50). Hence, we can write , where
k andm are integers. - Substitute back into the equation: .
- This simplifies to: .
- Dividing both sides by 50, we get: .
- This implies that is even, so must also be even. Thus, we can write .
- Now, both and are even, meaning they share a common factor of 2, which contradicts our initial assumption that was in simplest form.
Since our assumption leads to a contradiction, it must be false. Therefore, the square root of 50 is irrational.
Examples of Rational and Irrational Numbers
Understanding the distinction between rational and irrational numbers is essential in mathematics. Below are detailed examples to illustrate both types of numbers.
Rational Numbers
Rational numbers can be expressed as a fraction of two integers, where the denominator is not zero. They either terminate or repeat in their decimal form.
- Example 1:
- Fraction:
- Decimal: 0.5 (terminating)
- Example 2:
- Fraction:
- Decimal: 0.666... (repeating)
- Example 3: 4
- Fraction:
- Decimal: 4.0 (terminating)
Irrational Numbers
Irrational numbers cannot be expressed as a fraction of two integers. Their decimal forms are non-terminating and non-repeating.
- Example 1:
- Decimal: 1.41421356... (non-terminating, non-repeating)
- Example 2: (pi)
- Decimal: 3.14159265... (non-terminating, non-repeating)
- Example 3:
- Decimal: 7.07106781... (non-terminating, non-repeating)
Comparison Table
| Type | Number | Fraction Form | Decimal Form |
|---|---|---|---|
| Rational | 1/2 | 0.5 | |
| Rational | 2/3 | 0.666... | |
| Irrational | √2 | N/A | 1.41421356... |
| Irrational | π | N/A | 3.14159265... |
| Irrational | √50 | N/A | 7.07106781... |
These examples clearly illustrate the key differences between rational and irrational numbers, helping to deepen our understanding of their properties and applications in mathematics.
Historical Context of Irrational Numbers
The concept of irrational numbers has a rich historical background, tracing back to ancient civilizations and evolving significantly over centuries. Understanding this history provides insight into the development of mathematical thought and the acceptance of irrational numbers as a fundamental component of mathematics.
Ancient Greece
- Pythagoreans: The discovery of irrational numbers is often attributed to the Pythagoreans, a group of ancient Greek mathematicians and philosophers. They believed that all numbers could be expressed as the ratio of two integers. However, they encountered a problem with the diagonal of a square.
- Discovery of √2: While exploring the properties of a square, the Pythagoreans found that the length of the diagonal of a unit square (side length 1) could not be expressed as a ratio of two integers. This led to the realization that is irrational, causing a crisis in their belief system.
Classical Antiquity
- Euclid: In his work "Elements," Euclid provided a more formal treatment of irrational numbers. He described them as magnitudes that cannot be expressed as the ratio of two integers, and he demonstrated the irrationality of square roots of non-square numbers using geometric methods.
- Hippasus: According to legend, Hippasus, a Pythagorean philosopher, was the first to prove the irrationality of √2. His discovery was reportedly met with severe consequences, as it contradicted the Pythagorean belief that all numbers are rational.
Middle Ages
- Islamic Mathematicians: During the Islamic Golden Age, mathematicians such as Al-Khwarizmi and Omar Khayyam made significant contributions to algebra and the understanding of irrational numbers. They extended the work of Greek mathematicians and explored solutions to quadratic equations, which often involved irrational roots.
Renaissance and Beyond
- Renaissance Mathematicians: The revival of mathematical scholarship during the Renaissance led to further acceptance and exploration of irrational numbers. Mathematicians like Fibonacci included irrational numbers in their work, contributing to their wider acceptance.
- Modern Mathematics: With the development of calculus and real analysis, the understanding of irrational numbers became more rigorous. Mathematicians like Cantor and Dedekind provided formal definitions and proofs, solidifying the place of irrational numbers in modern mathematics.
Significance
The journey of irrational numbers from ancient skepticism to modern acceptance highlights the dynamic nature of mathematical discovery. Today, irrational numbers are recognized as essential components of the real number system, with crucial applications in various fields, including geometry, algebra, and calculus.
| Era | Key Figures | Contributions |
|---|---|---|
| Ancient Greece | Pythagoreans, Euclid, Hippasus | Discovery of √2, geometric proofs |
| Classical Antiquity | Euclid, Hippasus | Formal definitions, proofs of irrationality |
| Middle Ages | Al-Khwarizmi, Omar Khayyam | Algebraic solutions, exploration of irrationals |
| Renaissance and Beyond | Fibonacci, Cantor, Dedekind | Wider acceptance, formal definitions |
The historical development of irrational numbers underscores their profound impact on the advancement of mathematical theory and practice. Their acceptance marked a pivotal shift in understanding the nature of numbers and continues to influence modern mathematics.

Applications of Irrational Numbers in Real Life
Irrational numbers play a crucial role in various real-life applications. Despite their non-repeating, non-terminating nature, they are foundational in many scientific, engineering, and mathematical contexts.
- Engineering and Architecture: Irrational numbers like the square root of 50 (√50 ≈ 7.071) are often used in engineering and architecture to calculate precise measurements, angles, and dimensions. For instance, in structural engineering, accurate calculations of forces, lengths, and areas are essential for building safe structures.
- Physics: Many physical constants are irrational numbers. The square root of 2, for example, is critical in calculating the properties of waves and quantum mechanics. Similarly, √50 can be relevant in specific calculations involving distances or physical phenomena where precise square root values are needed.
- Mathematics and Geometry: In geometry, irrational numbers arise when dealing with non-perfect squares. The Pythagorean theorem, used to determine the length of the hypotenuse in a right-angled triangle, often results in an irrational number. For a triangle with legs of lengths 5 and 5, the hypotenuse would be √(5² + 5²) = √50.
- Art and Design: The golden ratio (approximately 1.6180339887), an irrational number, is widely used in art and design for its aesthetically pleasing properties. While not directly related to √50, the concept of irrational numbers in proportion and design is a parallel example of their importance.
- Computer Science: Algorithms for numerical methods, such as finding roots and optimizing functions, often require the use of irrational numbers for precise calculations. In graphics rendering, square roots and other irrational values are crucial for generating realistic images and simulations.
- Finance: In financial mathematics, irrational numbers can appear in models that require continuous compounding of interest or in the pricing of complex financial derivatives, where precise calculations of growth rates and probabilities are necessary.
Overall, irrational numbers, including the square root of 50, are indispensable in various fields, ensuring accuracy and precision in theoretical and applied contexts.
Video này giải thích lý do tại sao căn bậc hai của 50 là một số vô tỷ, với các ví dụ và chứng minh toán học.
Tại sao Căn bậc hai của 50 Không phải là Số hữu tỷ
READ MORE:
Video này giải thích những căn bậc hai nào không phải là số hữu tỷ, với các ví dụ và chứng minh toán học.
Những Căn Bậc Hai Nào Không Phải Là Số Hữu Tỷ