Is Square Root of 18 a Rational Number? Discover the Truth!

To determine whether the square root of 18 is a rational number, we need to understand the definition of rational and irrational numbers:

• A rational number can be expressed as a fraction of two integers, where the denominator is not zero.
• An irrational number cannot be expressed as a simple fraction. It has a non-repeating, non-terminating decimal expansion.

Square Root of 18

The square root of 18 is represented as \(\sqrt{18}\).

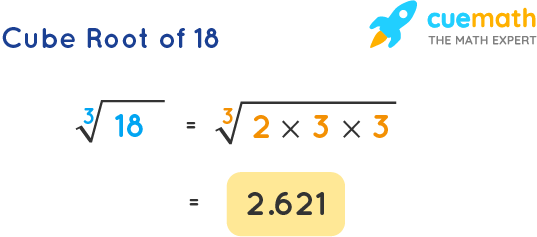
Let's simplify \(\sqrt{18}\):

\[\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}\]

Since \(\sqrt{2}\) is known to be an irrational number (it cannot be expressed as a fraction and has a non-repeating, non-terminating decimal expansion), multiplying it by 3 does not change its irrationality.

Conclusion

Therefore, \(\sqrt{18}\) is not a rational number. It is an irrational number because it simplifies to \(3\sqrt{2}\), where \(\sqrt{2}\) is irrational.

In mathematics, understanding the distinction between rational and irrational numbers is fundamental. These concepts help us classify and comprehend various types of numbers.

Rational numbers are numbers that can be expressed as a fraction \(\frac{a}{b}\), where \(a\) and \(b\) are integers and \(b \neq 0\). Rational numbers include:

• Integers (e.g., -3, 0, 4)
• Fractions (e.g., \(\frac{1}{2}\), \(\frac{3}{4}\))
• Finite decimals (e.g., 0.5, 0.75)
• Repeating decimals (e.g., 0.333..., 1.666...)

Irrational numbers cannot be expressed as a simple fraction. They have non-repeating, non-terminating decimal expansions. Examples include:

• \(\pi\) (Pi)
• \(e\) (Euler's number)
• \(\sqrt{2}\) (the square root of 2)

The concept of rational and irrational numbers extends to understanding square roots. While some square roots, like \(\sqrt{4} = 2\), are rational, many are irrational. For instance, \(\sqrt{2}\) is irrational because it cannot be precisely written as a fraction.

In the following sections, we will explore whether the square root of 18 falls into the category of rational or irrational numbers.

The square root function is a fundamental concept in mathematics, represented by the symbol \(\sqrt{}\). It is used to determine a number which, when multiplied by itself, yields the original number. For any non-negative number \(x\), the square root of \(x\) is denoted as \(\sqrt{x}\) and is defined as follows:

\[\sqrt{x} = y \quad \text{if and only if} \quad y^2 = x \]

Let's explore the properties and implications of the square root function:

• Non-negative Results: The square root of a non-negative number is always non-negative. For example, \(\sqrt{4} = 2\) and \(\sqrt{0} = 0\).
• Perfect Squares: If \(x\) is a perfect square (i.e., \(x = n^2\) for some integer \(n\)), then \(\sqrt{x}\) is an integer. Examples include \(\sqrt{1} = 1\), \(\sqrt{4} = 2\), and \(\sqrt{9} = 3\).
• Non-perfect Squares: If \(x\) is not a perfect square, \(\sqrt{x}\) is an irrational number. For example, \(\sqrt{2}\) and \(\sqrt{3}\) cannot be expressed as exact fractions.

Now, consider the square root of 18:

\[\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}\]

Since \(\sqrt{2}\) is an irrational number, multiplying it by 3 (a rational number) results in \(3\sqrt{2}\), which remains irrational.

Understanding the square root function helps in identifying whether a given square root is rational or irrational. In the next section, we will delve deeper into the classification of numbers to determine the nature of the square root of 18.

Simplifying square roots is a useful skill in mathematics, especially when working with non-perfect squares. To simplify the square root of a number, we look for factors that are perfect squares. Let's simplify the square root of 18 step by step:

1. First, express 18 as a product of its prime factors:

\[18 = 2 \times 3^2\]

2. Next, apply the square root to the factorized form:

\[\sqrt{18} = \sqrt{2 \times 3^2}\]

3. Separate the factors under the square root into two groups, one of which is a perfect square:

\[\sqrt{18} = \sqrt{2} \times \sqrt{3^2}\]

4. Simplify the square root of the perfect square (3²):

\[\sqrt{3^2} = 3\]

5. Combine the simplified square roots:

\[\sqrt{18} = 3 \times \sqrt{2}\]

Thus, the simplified form of \(\sqrt{18}\) is \(3\sqrt{2}\).

Since \(\sqrt{2}\) is an irrational number, \(3\sqrt{2}\) is also irrational. This demonstrates that \(\sqrt{18}\) cannot be expressed as a rational number.

Simplifying square roots allows us to better understand their properties and classifications. In this case, the simplification process reveals that \(\sqrt{18}\) is irrational. This step-by-step approach can be applied to other square roots to determine their nature.

Rational numbers are a fundamental concept in mathematics, representing numbers that can be expressed as the quotient of two integers. To understand rational numbers, let's break down their definition and properties step by step:

1. Definition:

   A rational number is any number that can be written in the form \(\frac{a}{b}\), where \(a\) and \(b\) are integers and \(b \neq 0\). This form is known as a fraction.

2. Examples of Rational Numbers:
   • Integers: Any integer \(n\) can be written as \(\frac{n}{1}\). For example, 5 is a rational number because it can be expressed as \(\frac{5}{1}\).
   • Proper Fractions: Numbers like \(\frac{1}{2}\) and \(\frac{3}{4}\) are rational because both the numerator and the denominator are integers.
   • Improper Fractions: Numbers like \(\frac{7}{3}\) are also rational for the same reason.
   • Finite Decimals: Any finite decimal can be converted into a fraction. For example, 0.75 is \(\frac{3}{4}\).
   • Repeating Decimals: Numbers with repeating decimal patterns, such as 0.333... (which equals \(\frac{1}{3}\)) and 1.666... (which equals \(\frac{5}{3}\)), are rational.
3. Properties of Rational Numbers:
   • Closure: The sum, difference, product, and quotient (except division by zero) of two rational numbers is always a rational number.
   • Density: Between any two rational numbers, there exists another rational number. This means rational numbers are densely packed on the number line.
   • Decimal Expansion: Rational numbers have decimal expansions that either terminate or repeat.
4. Non-examples:

   Numbers that cannot be expressed as a simple fraction are not rational. These include most square roots (e.g., \(\sqrt{2}\)), \(\pi\), and \(e\). These numbers are classified as irrational.

By understanding rational numbers and their properties, we can better analyze and classify other numbers. This knowledge is crucial for distinguishing between rational and irrational numbers, such as determining whether the square root of 18 is rational or not.

An irrational number is a real number that cannot be expressed as a simple fraction or ratio of two integers. They possess several distinctive characteristics:

1. Non-terminating Decimal Representation: Irrational numbers have decimal representations that neither terminate (end) nor repeat. For example, the square root of 2, approximately 1.414213562373095, continues indefinitely without settling into a pattern.
2. Non-repeating Decimals: Unlike rational numbers, which have repeating decimal patterns, irrational numbers do not repeat any finite sequence of digits indefinitely.
3. Unpredictable Sequence: The digits in the decimal expansion of an irrational number appear in an apparently random sequence without any predictable pattern.
4. Cannot Be Represented as Fractions: Irrational numbers defy representation as a ratio of two integers. This fundamental characteristic distinguishes them from rational numbers, which can be expressed in such a form.
5. Existence Between Integers: Irrational numbers populate the number line densely between consecutive integers, implying there are infinitely many irrational numbers between any two rational numbers.
6. Proof of Irrationality: To establish the irrationality of a specific number, mathematical proofs rely on contradiction, showing that assuming the number is rational leads to a logical inconsistency.

The square root of 18 is an irrational number, which means it cannot be expressed as a simple fraction of two integers. Here are some properties related to the square root of 18:

• Decimal Representation: The square root of 18 is approximately 4.242640687119285. Its decimal representation neither terminates nor repeats, characteristic of irrational numbers.
• Non-Integer Nature: Unlike perfect squares (like 9 or 16), the square root of 18 is not an integer. It falls between integers 4 and 5 on the number line.
• Non-Rational: Despite being a square root, 18 does not have a square root that is a rational number. This is proven by its non-terminating and non-repeating decimal nature.
• Mathematical Context: In mathematical proofs, the irrationality of the square root of 18 can be demonstrated using methods that show it cannot be expressed as a fraction of integers.
• Application in Geometry: The square root of 18 is used in geometric calculations, such as determining diagonal lengths of squares or rectangles with side lengths of 9 units each.

To prove that the square root of 18 is irrational, we can use a mathematical argument that demonstrates it cannot be expressed as a fraction of two integers. Here's a structured approach to prove the irrationality:

1. Assume Contradiction: Suppose √18 is rational, meaning it can be expressed as √18 = p/q where p and q are integers with no common factors (other than 1) and q ≠ 0.
2. Square Both Sides: Squaring both sides gives us 18 = p²/q².
3. Rearrange and Simplify: Multiplying both sides by q² results in 18q² = p².
4. Analysis of Prime Factors: Analyze the prime factorization of 18 and p². Since 18 = 2 × 3², p² must also be divisible by 2 and 3, implying p is divisible by 2 and/or 3.
5. Contradiction: This contradicts our assumption that p and q have no common factors, proving that √18 cannot be expressed as a ratio of two integers.

Irrational numbers have practical applications in various real-life scenarios where precise and non-repeating values are essential. Here are some examples:

• Geometry: Irrational numbers such as the square root of 2 are crucial in geometric calculations involving lengths of diagonals in squares and rectangles.
• Engineering: Engineers use irrational numbers in structural design and calculations requiring accurate measurements, where approximations based on rational numbers would not suffice.
• Physics: The value of π (pi), an irrational number, is fundamental in physics formulas involving circles, spheres, and oscillatory motion.
• Computing: In computer science and digital technology, irrational numbers are used in algorithms for graphics rendering, signal processing, and cryptography.
• Finance: Financial models utilize irrational numbers for calculating interest, growth rates, and risk assessments that demand precise numerical values.
• Art and Design: Artists and designers apply irrational numbers in creating aesthetically pleasing shapes and patterns based on mathematical principles.

Understanding the distinctions between rational and irrational numbers can help clarify several common misconceptions:

• All Square Roots are Rational: A common misconception is that all square roots, including those of non-perfect squares like 18, are rational. In reality, only square roots of perfect squares (like 9, 16, etc.) are rational.
• Irrational Numbers are Insignificant: Some believe irrational numbers are purely theoretical or less practical than rational numbers. However, they are essential in mathematics and have numerous real-world applications.
• Rational Numbers are Finite: Another misconception is that rational numbers have finite decimal representations. While some do (like 0.5 or 0.75), others have repeating decimals (like 1/3 = 0.333...).
• Rational Numbers are Always Whole Numbers: Contrary to this belief, rational numbers can be fractions or decimals, including non-integer values such as 0.5 or -2.75.
• Application Limitations: Some assume irrational numbers have limited practical applications. However, they are indispensable in fields such as science, engineering, and finance for precise calculations and modeling.

Here are some frequently asked questions about rational and irrational numbers:

1. What is the difference between rational and irrational numbers?

   Rational numbers can be expressed as a ratio of two integers, while irrational numbers cannot and have non-terminating, non-repeating decimal expansions.

2. Is the square root of 18 a rational number?

   No, the square root of 18 is irrational. It cannot be expressed as a fraction of two integers.

3. Why are irrational numbers important?

   Irrational numbers are crucial in mathematics and various practical fields for precise calculations where exact values are needed, such as in geometry, physics, and engineering.

4. Can irrational numbers be represented in decimal form?

   Yes, irrational numbers have decimal representations that neither terminate nor repeat. Examples include π (pi) and √2.

5. How do you prove a number is irrational?

   A common method is proof by contradiction, assuming the number is rational and showing that this assumption leads to a logical inconsistency.