Simplify Square Roots with Variables: Mastering the Basics and Beyond

Topic simplify square roots with variables: Simplifying square roots with variables can seem daunting, but with the right approach, it becomes much more manageable. This guide will walk you through the basic properties, techniques, and common pitfalls, providing clear examples and practice problems to help you master the process of simplifying square roots involving variables.

Introduction to Simplifying Square Roots with Variables

Simplifying square roots with variables involves breaking down the expression under the radical sign into its prime factors and extracting the square roots of the perfect squares. This process makes the expression simpler and more manageable.

Factor the Expression: Find the prime factors of the number and the variables under the square root.
Identify Perfect Squares: Look for pairs of factors since the square root of a pair is a single factor outside the square root.
Rewrite the Expression: Separate the perfect squares from the non-perfect squares and simplify.
Simplify: Multiply the factors outside the square root and keep the remaining factors inside the square root.

Examples

Example 1: Simplifying $ \sqrt{9x^6} $

Factor the expression:

$ \sqrt{9x^6} = \sqrt{3^2 \cdot (x^3)^2} $

Separate the perfect squares and simplify:

$ \sqrt{3^2} \cdot \sqrt{(x^3)^2} = 3|x^3| $

Answer: $ 3|x^3| $

Example 2: Simplifying $ \sqrt{100x^2y^4} $

Factor the expression:

$ \sqrt{100x^2y^4} = \sqrt{10^2 \cdot x^2 \cdot (y^2)^2} $

Separate the perfect squares and simplify:

$ \sqrt{10^2} \cdot \sqrt{x^2} \cdot \sqrt{(y^2)^2} = 10|x|y^2 $

Answer: $ 10|x|y^2 $

Example 3: Simplifying $ \sqrt{49x^{10}y^8} $

Factor the expression:

$ \sqrt{49x^{10}y^8} = \sqrt{7^2 \cdot (x^5)^2 \cdot (y^4)^2} $

Separate the perfect squares and simplify:

$ \sqrt{7^2} \cdot \sqrt{(x^5)^2} \cdot \sqrt{(y^4)^2} = 7|x^5|y^4 $

Answer: $ 7|x^5|y^4 $

Conclusion

By breaking down the variables and constants into their prime factors and identifying perfect squares, you can simplify complex radical expressions involving variables. This process not only makes calculations easier but also helps in understanding the structure of algebraic expressions more deeply.

Steps to Simplify Square Roots with Variables

Factor the Expression: Find the prime factors of the number and the variables under the square root.
Identify Perfect Squares: Look for pairs of factors since the square root of a pair is a single factor outside the square root.
Rewrite the Expression: Separate the perfect squares from the non-perfect squares and simplify.
Simplify: Multiply the factors outside the square root and keep the remaining factors inside the square root.

Examples

Example 1: Simplifying $ \sqrt{9x^6} $

Factor the expression:

$ \sqrt{9x^6} = \sqrt{3^2 \cdot (x^3)^2} $

Separate the perfect squares and simplify:

$ \sqrt{3^2} \cdot \sqrt{(x^3)^2} = 3|x^3| $

Answer: $ 3|x^3| $

Example 2: Simplifying $ \sqrt{100x^2y^4} $

Factor the expression:

$ \sqrt{100x^2y^4} = \sqrt{10^2 \cdot x^2 \cdot (y^2)^2} $

Separate the perfect squares and simplify:

$ \sqrt{10^2} \cdot \sqrt{x^2} \cdot \sqrt{(y^2)^2} = 10|x|y^2 $

Answer: $ 10|x|y^2 $

Example 3: Simplifying $ \sqrt{49x^{10}y^8} $

Factor the expression:

$ \sqrt{49x^{10}y^8} = \sqrt{7^2 \cdot (x^5)^2 \cdot (y^4)^2} $

Separate the perfect squares and simplify:

$ \sqrt{7^2} \cdot \sqrt{(x^5)^2} \cdot \sqrt{(y^4)^2} = 7|x^5|y^4 $

Answer: $ 7|x^5|y^4 $

Conclusion

Examples

Example 1: Simplifying $ \sqrt{9x^6} $

Factor the expression:

$ \sqrt{9x^6} = \sqrt{3^2 \cdot (x^3)^2} $

Separate the perfect squares and simplify:

$ \sqrt{3^2} \cdot \sqrt{(x^3)^2} = 3|x^3| $

Answer: $ 3|x^3| $

Example 2: Simplifying $ \sqrt{100x^2y^4} $

Factor the expression:

$ \sqrt{100x^2y^4} = \sqrt{10^2 \cdot x^2 \cdot (y^2)^2} $

Separate the perfect squares and simplify:

$ \sqrt{10^2} \cdot \sqrt{x^2} \cdot \sqrt{(y^2)^2} = 10|x|y^2 $

Answer: $ 10|x|y^2 $

Example 3: Simplifying $ \sqrt{49x^{10}y^8} $

Factor the expression:

$ \sqrt{49x^{10}y^8} = \sqrt{7^2 \cdot (x^5)^2 \cdot (y^4)^2} $

Separate the perfect squares and simplify:

$ \sqrt{7^2} \cdot \sqrt{(x^5)^2} \cdot \sqrt{(y^4)^2} = 7|x^5|y^4 $

Answer: $ 7|x^5|y^4 $

Conclusion

Introduction

Simplifying square roots with variables is a crucial skill in algebra that helps to make complex expressions more manageable. This process involves breaking down the expression under the square root into its prime factors and then simplifying by removing perfect squares. Understanding the properties of square roots and how they interact with variables is essential for success in higher-level math.

In this guide, we will cover the basic principles of simplifying square roots with variables, starting with single variables and moving to more complex expressions involving multiple variables and exponents. We will provide step-by-step examples to illustrate each concept, ensuring that you gain a solid understanding of the techniques involved.

By mastering these techniques, you'll be able to simplify a wide range of algebraic expressions, making them easier to work with and solve. Let's begin our journey into the world of simplifying square roots with variables.

Understanding Square Roots

Square roots are a fundamental concept in mathematics, particularly in algebra. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4 because 4 multiplied by 4 equals 16. This can be represented as:

\[\sqrt{16} = 4\]

When dealing with variables, the concept remains the same. The square root of $x^2$ is $x$, as shown below:

\[\sqrt{x^2} = x\]

Here are some key points to understand about square roots:

Principal Square Root: The non-negative square root of a number. For instance, the principal square root of 9 is 3, represented as $\sqrt{9} = 3$.
Radicand: The number or expression inside the square root symbol. In $\sqrt{x^2}$, $x^2$ is the radicand.
Perfect Squares: Numbers like 1, 4, 9, 16, etc., whose square roots are integers.

Understanding how to simplify square roots is crucial, especially when variables are involved. Simplifying square roots with variables involves the following steps:

Identify and separate the perfect square factors from the radicand.
Apply the square root to both the numerical and variable parts.
Simplify the expression by removing the square root of the perfect squares.

For example, to simplify $\sqrt{18x^4}$, follow these steps:

Separate the perfect square factors: $18x^4 = 9 \cdot 2 \cdot x^4 = 3^2 \cdot 2 \cdot (x^2)^2$.
Apply the square root: $\sqrt{18x^4} = \sqrt{3^2 \cdot 2 \cdot (x^2)^2}$.
Simplify: $\sqrt{18x^4} = 3x^2\sqrt{2}$.

This process helps in breaking down complex expressions and making calculations easier.

Basic Properties of Square Roots

The square root is a fundamental mathematical operation that can be applied to both numerical and variable expressions. Understanding its basic properties is crucial for simplifying complex expressions.

Product Property: The square root of a product is the product of the square roots.

$\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}$

Quotient Property: The square root of a quotient is the quotient of the square roots.

$\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \quad \text{for} \quad b \ne 0$

Power of a Variable: When dealing with variables, the square root of a variable raised to an even power is the variable raised to half that power.

$\sqrt{x^{2n}} = x^n$

Absolute Value: When the variable is raised to an odd power, it must be expressed in terms of the absolute value to ensure non-negativity.

$\sqrt{x^{2n+1}} = x^n \cdot \sqrt{x} \quad \text{or} \quad \sqrt{x^2} = |x|$

These properties simplify the process of working with square roots in algebraic expressions, especially when variables are involved. Mastering these will help in solving more complex mathematical problems.

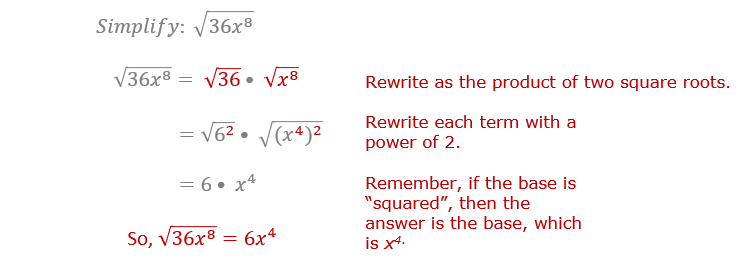
Square Roots Involving Variables

Understanding how to simplify square roots involving variables is essential for mastering algebra. This section will guide you through the process of dealing with square roots that contain variables, step-by-step.

Identify Perfect Squares:
When simplifying square roots with variables, start by identifying any perfect square factors within the radicand (the number or expression inside the square root). For example, in $\sqrt{16x^2}$, 16 and $x^2$ are both perfect squares.
Simplify Each Perfect Square:
Take the square root of each perfect square factor. For $\sqrt{16x^2}$, this becomes $4x$, since $\sqrt{16} = 4$ and $\sqrt{x^2} = x$.
Recombine Remaining Factors:
If there are any remaining factors that are not perfect squares, leave them under the square root symbol. For example, $\sqrt{32x^3}$ can be broken down into $\sqrt{16x^2 \cdot 2x}$, which simplifies to $4x\sqrt{2x}$.
Combine Simplified Parts:
Combine the simplified parts for the final expression. Ensure all parts outside the square root are multiplied together. For instance, $\sqrt{18x^4y}$ can be simplified to $3x^2\sqrt{2y}$, where 18 is factored into $9 \times 2$ and $x^4$ is a perfect square.

By following these steps, you can effectively simplify square roots involving variables. Practice with various expressions to become more comfortable with the process.

Simplifying Square Roots of Single Variables

When simplifying the square roots of single variables, it is important to understand the basic properties and rules that govern these operations. Here are the steps to follow:

Identify the Variable and its Exponent: Consider a variable $ x $ with an exponent $ n $. For example, $ \sqrt{x^6} $.
Apply the Square Root Rule: The square root of $ x^n $ is $ x^{n/2} $. So, $ \sqrt{x^6} = x^{6/2} = x^3 $.
Handling Even and Odd Exponents:
- If the exponent is even, simply divide the exponent by 2. For example, $ \sqrt{x^8} = x^4 $.
- If the exponent is odd, rewrite the variable as the product of a square and another variable. For example, $ \sqrt{x^7} = \sqrt{x^6 \cdot x} = x^3 \sqrt{x} $.

Here are a few examples:

Expression	Simplified Form
$\sqrt{x^4}$	$x^2$
$\sqrt{x^9}$	$x^4 \sqrt{x}$
$\sqrt{x^{10}}$	$x^5$

By following these steps, you can simplify square roots involving single variables effectively, making your algebraic manipulations easier and more efficient.

Simplifying Square Roots of Multiple Variables

Simplifying square roots of multiple variables involves breaking down each variable into its prime factors and pairing identical factors. This process can be done step-by-step to ensure accuracy and simplicity.

Identify and group the variables under the square root. For example, consider the expression $ \sqrt{50x^4y^6} $.
Factorize the numerical part and the variables. Here, $ 50 = 2 \cdot 25 = 2 \cdot 5^2 $, and $ x^4 = (x^2)^2 $, $ y^6 = (y^3)^2 $.
Rewrite the expression to highlight the squares:

$ \sqrt{50x^4y^6} = \sqrt{2 \cdot 5^2 \cdot (x^2)^2 \cdot (y^3)^2} $
Separate the perfect squares from the rest:

$ \sqrt{2} \cdot \sqrt{5^2} \cdot \sqrt{(x^2)^2} \cdot \sqrt{(y^3)^2} $
Simplify each square root:

$ \sqrt{2} \cdot 5 \cdot x^2 \cdot y^3 $
Combine the simplified terms:

$ 5x^2y^3\sqrt{2} $

In summary, the simplified form of $ \sqrt{50x^4y^6} $ is $ 5x^2y^3\sqrt{2} $. This method can be applied to any expression involving multiple variables by identifying pairs of identical factors and extracting them from under the radical sign.

Simplifying Square Roots with Exponents

When simplifying square roots with exponents, understanding the relationship between radicals and exponents is crucial. Here are the basic steps to simplify such expressions:

Identify the exponent and the radicand.
Express the square root using a rational exponent. For example, the square root of $x^a$ can be written as $x^{a/2}$.
Simplify the exponent if possible.

Here are some examples to illustrate the process:

$\sqrt{x^4} = x^{4/2} = x^2$
$\sqrt{x^6} = x^{6/2} = x^3$
$\sqrt{x^{10}} = x^{10/2} = x^5$

In cases where the exponent is not even, factor the radicand so that one part has an even exponent:

Example: $\sqrt{x^5} = \sqrt{x^4 \cdot x} = \sqrt{x^4} \cdot \sqrt{x} = x^2 \sqrt{x}$

By converting radicals to exponents, we can more easily apply exponent rules and simplify the expressions.

Simplifying Square Roots of Fractional Expressions

Simplifying square roots of fractional expressions can initially seem challenging, but by following a structured approach, it becomes manageable. Here’s a step-by-step guide to help you simplify these expressions effectively.

Identify the numerator and the denominator separately.
Apply the square root to both the numerator and the denominator individually.
Simplify each square root separately.
Combine the simplified results to get the final expression.

Let's illustrate this with an example:

Simplify $ \sqrt{\frac{9x^4}{16y^2}} $.

Step 1: Identify the numerator and the denominator.
- Numerator: $9x^4$
- Denominator: $16y^2$
Step 2: Apply the square root to both.
- $ \sqrt{9x^4} $ and $ \sqrt{16y^2} $
Step 3: Simplify each square root.
- $ \sqrt{9x^4} = 3x^2 $ (since $ \sqrt{9} = 3 $ and $ \sqrt{x^4} = x^2 $)
- $ \sqrt{16y^2} = 4y $ (since $ \sqrt{16} = 4 $ and $ \sqrt{y^2} = y $)
Step 4: Combine the results.
- $ \sqrt{\frac{9x^4}{16y^2}} = \frac{3x^2}{4y} $

Therefore, $ \sqrt{\frac{9x^4}{16y^2}} = \frac{3x^2}{4y} $.

This approach can be generalized to more complex fractional expressions involving variables. By breaking down the expression and simplifying each part individually, you can effectively manage and simplify fractional square roots.

Using the Quotient Property

The quotient property of square roots allows us to simplify the square root of a fraction by separating it into the square roots of the numerator and the denominator. This property is especially useful when dealing with variables and can be expressed as follows:

$$\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$$

Here’s a step-by-step guide on how to use the quotient property to simplify square roots:

Simplify the fraction in the radicand if possible: Before applying the quotient property, check if the fraction can be simplified. This makes the subsequent steps easier.

Example: Simplify $$\sqrt{\frac{72z^{12}}{2z^{10}}}$$.

First, simplify the fraction inside the radical:

$$\frac{72z^{12}}{2z^{10}} = 36z^2$$

So, $$\sqrt{36z^2} = 6z$$.
Use the quotient property to separate the radicals: Rewrite the square root of the fraction as the quotient of two separate square roots.

Example: Simplify $$\sqrt{\frac{27m^3}{196}}$$.

Use the quotient property:

$$\sqrt{\frac{27m^3}{196}} = \frac{\sqrt{27m^3}}{\sqrt{196}}$$
Simplify the numerator and the denominator: Simplify the square roots of both the numerator and the denominator.

Continuing from the example above:

$$\frac{\sqrt{27m^3}}{\sqrt{196}} = \frac{3m\sqrt{3m}}{14}$$

Since 196 is a perfect square (14^2), its square root is 14, and we simplified $$\sqrt{27m^3}$$ as $$3m\sqrt{3m}$$.

Here are a few more examples to illustrate the process:

Example 1: Simplify $$\sqrt{\frac{21}{64}}$$.

Rewrite using the quotient property:

$$\frac{\sqrt{21}}{\sqrt{64}} = \frac{\sqrt{21}}{8}$$
Example 2: Simplify $$\sqrt{\frac{24p^3}{49}}$$.

Rewrite using the quotient property:

$$\frac{\sqrt{24p^3}}{\sqrt{49}} = \frac{2p\sqrt{6p}}{7}$$
Example 3: Simplify $$\sqrt{\frac{54u^7}{v^8}}$$.

Rewrite using the quotient property:

$$\frac{\sqrt{54u^7}}{\sqrt{v^8}} = \frac{3u^3\sqrt{6u}}{v^4}$$