Topic how to find the perimeter of a regular polygon: Discover how to find the perimeter of a regular polygon with ease. Our comprehensive guide explains the formula and steps involved, making it simple for anyone to calculate the perimeter of any regular polygon. Whether you're a student or just curious, this article will help you master the concept quickly and effectively.
Table of Content
- How to Find the Perimeter of a Regular Polygon
- Introduction to Regular Polygons
- Understanding the Perimeter
- Formula for Perimeter of Regular Polygons
- Example Calculations
- Applications of Perimeter in Real Life
- Perimeter Formulas for Different Regular Polygons
- Common Mistakes and How to Avoid Them
- Practice Problems
- Advanced Topics
- YOUTUBE: Hướng dẫn cách tính chu vi các đa giác một cách chi tiết và dễ hiểu. Video phù hợp cho những ai muốn học cách tính chu vi của các đa giác đều.
How to Find the Perimeter of a Regular Polygon
A regular polygon is a polygon with all sides and angles equal. The perimeter of a regular polygon can be easily calculated using the formula:
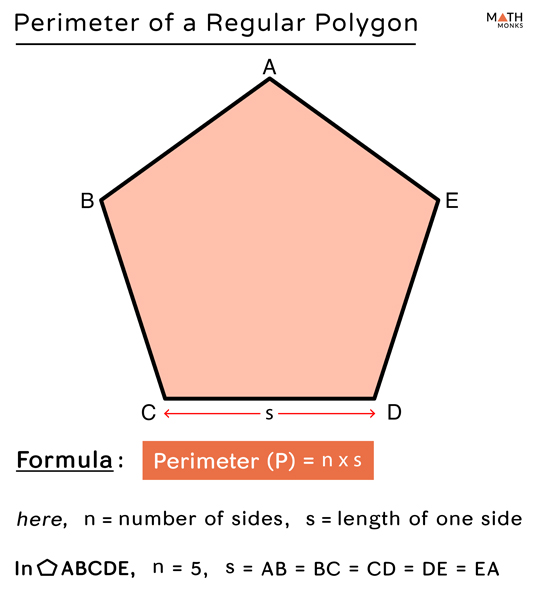
\[ \text{Perimeter} = n \times s \]
where:
- \( n \) is the number of sides
- \( s \) is the length of one side
Steps to Calculate the Perimeter
Identify the number of sides (\( n \)) of the polygon.
Measure the length of one side (\( s \)).
Use the formula \(\text{Perimeter} = n \times s\) to find the perimeter.
Example Calculation
Let's find the perimeter of a regular hexagon (6-sided polygon) where each side is 5 cm long:
\[ n = 6, \quad s = 5 \, \text{cm} \]
Using the formula:
\[ \text{Perimeter} = 6 \times 5 = 30 \, \text{cm} \]
Perimeter Formulas for Common Regular Polygons
| Polygon | Number of Sides (\( n \)) | Perimeter Formula |
|---|---|---|
| Equilateral Triangle | 3 | \( P = 3s \) |
| Square | 4 | \( P = 4s \) |
| Pentagon | 5 | \( P = 5s \) |
| Hexagon | 6 | \( P = 6s \) |
Conclusion
Calculating the perimeter of a regular polygon is straightforward when you know the number of sides and the length of one side. Use the formula \( \text{Perimeter} = n \times s \) for quick and accurate results.
READ MORE:
Introduction to Regular Polygons
A regular polygon is a geometric figure with all sides and angles equal. Common examples include the equilateral triangle, the square, and the regular pentagon. These shapes have unique properties that make them fundamental in geometry and other mathematical applications.
Regular polygons are highly symmetrical. Each angle bisector, perpendicular bisector, and median intersect at a single point, known as the center. This center is equidistant from all vertices, making the regular polygon both inscribed and circumscribed about circles.
The sides of a regular polygon form congruent isosceles triangles with the center, which aids in calculating various properties like area and perimeter. Understanding the basics of regular polygons is crucial for exploring more complex geometric concepts.
Understanding the Perimeter
The perimeter of a polygon is the total length around the boundary of the shape. For regular polygons, where all sides are of equal length, the perimeter can be easily calculated using a specific formula.
The formula to find the perimeter \( P \) of a regular polygon is given by:
\[ P = n \times s \]
where \( n \) is the number of sides and \( s \) is the length of one side.
Let's break down the process step by step:
- Identify the number of sides (n): Determine how many sides the polygon has. For example, a pentagon has 5 sides, a hexagon has 6 sides, and so on.
- Measure the length of one side (s): If all sides are of equal length, measure the length of any one side.
- Apply the formula: Multiply the number of sides by the length of one side to find the perimeter. For instance, if each side of a regular hexagon is 4 cm long, the perimeter would be: \[ P = 6 \times 4 = 24 \text{ cm} \]
This straightforward method makes it simple to calculate the perimeter of any regular polygon, ensuring you can quickly determine the total distance around the shape.
Formula for Perimeter of Regular Polygons
A regular polygon is a polygon with all sides and angles equal. To find the perimeter of a regular polygon, you can use a straightforward formula that involves the number of sides and the length of each side. Here's how you can do it:
- Identify the number of sides (\(n\)) of the regular polygon.
- Measure the length of one side (\(a\)).
- Use the formula:
\[
\text{Perimeter} = n \times a
\]
Let's go through an example:
Suppose you have a regular hexagon (6 sides) and each side is 5 units long. To find the perimeter, use the formula:
\[
\text{Perimeter} = 6 \times 5 = 30 \text{ units}
\]
This formula applies to any regular polygon, whether it's a triangle (3 sides), a square (4 sides), a pentagon (5 sides), or any \(n\)-sided regular polygon.
| Polygon | Number of Sides (\(n\)) | Perimeter Formula |
|---|---|---|
| Triangle | 3 | \(P = 3 \times a\) |
| Square | 4 | \(P = 4 \times a\) |
| Pentagon | 5 | \(P = 5 \times a\) |
| Hexagon | 6 | \(P = 6 \times a\) |
| \(n\)-sided Polygon | \(n\) | \(P = n \times a\) |
Understanding this formula can help you quickly find the perimeter of any regular polygon, making your calculations more efficient and accurate.
Example Calculations
Understanding how to calculate the perimeter of regular polygons is crucial for various mathematical and practical applications. Let's walk through some example calculations to illustrate this process clearly.
| Polygon Type | Side Length (L) | Number of Sides (n) | Perimeter Formula | Calculation | Perimeter (P) |
|---|---|---|---|---|---|
| Square | 5 cm | 4 | \(P = n \times L\) | \(P = 4 \times 5\) | 20 cm |
| Hexagon | 6 cm | 6 | \(P = n \times L\) | \(P = 6 \times 6\) | 36 cm |
| Pentagon | 7 cm | 5 | \(P = n \times L\) | \(P = 5 \times 7\) | 35 cm |
Each calculation follows the simple formula \(P = n \times L\), where \(n\) is the number of sides, and \(L\) is the length of one side. This formula makes it easy to determine the perimeter of any regular polygon as long as you know these two values.

Applications of Perimeter in Real Life
The perimeter of a regular polygon is a fundamental concept in various real-life applications. Understanding how to calculate the perimeter can be useful in multiple fields and everyday scenarios. Here are some detailed applications:
-
Architecture and Construction
In architecture and construction, the perimeter of polygons is used to determine the amount of materials needed for building structures. For example:
- Calculating the total length of fencing required for a polygonal garden or yard.
- Estimating the quantity of baseboard or crown molding needed to cover the perimeter of a room.
- Determining the boundary length for constructing pathways or driveways around a property.
-
Landscaping
Landscapers often use perimeter calculations for designing gardens and outdoor spaces. This includes:
- Planning the layout and length of hedges or flower beds along the edges of a polygonal area.
- Designing and outlining walking paths, patios, and decks with specific perimeter dimensions.
-
Interior Design
Interior designers use the perimeter of rooms to make informed decisions about decorations and furnishings, such as:
- Measuring the perimeter for installing wallpaper or painting borders.
- Arranging furniture and ensuring that it fits well within the defined space.
- Planning the installation of lighting fixtures or electrical outlets along the room's perimeter.
-
Sports and Recreation
In sports and recreational activities, the perimeter plays a role in marking boundaries and planning spaces, including:
- Designing the layout of sports fields, courts, and tracks with precise boundary measurements.
- Setting up perimeter markers for safe zones in various outdoor activities and games.
-
Urban Planning
Urban planners use perimeter calculations for developing and managing public spaces, such as:
- Designing parks, plazas, and public squares with accurate boundary measurements.
- Planning the placement of benches, streetlights, and other fixtures along walkways and boundaries.
In summary, knowing how to find the perimeter of a regular polygon is an essential skill that can be applied in various real-life contexts to achieve precise and functional designs.
Perimeter Formulas for Different Regular Polygons
Regular polygons have equal sides and equal angles, making their perimeter calculations straightforward. Below are the perimeter formulas for various regular polygons:
- Triangle (Equilateral)
- Square
- Pentagon
- Hexagon
- Heptagon
- Octagon
- Nonagon
- Decagon
- Undecagon
- Dodecagon
For an equilateral triangle with side length \( s \):
\[ P = 3s \]
For a square with side length \( s \):
\[ P = 4s \]
For a regular pentagon with side length \( s \):
\[ P = 5s \]
For a regular hexagon with side length \( s \):
\[ P = 6s \]
For a regular heptagon with side length \( s \):
\[ P = 7s \]
For a regular octagon with side length \( s \):
\[ P = 8s \]
For a regular nonagon with side length \( s \):
\[ P = 9s \]
For a regular decagon with side length \( s \):
\[ P = 10s \]
For a regular undecagon with side length \( s \):
\[ P = 11s \]
For a regular dodecagon with side length \( s \):
\[ P = 12s \]
These formulas are derived from the general perimeter formula for any regular polygon:
\[ P = n \cdot s \]
where \( n \) is the number of sides, and \( s \) is the length of one side.
Using these formulas, you can easily calculate the perimeter of any regular polygon if you know the number of sides and the length of each side.
Common Mistakes and How to Avoid Them
When calculating the perimeter of regular polygons, several common mistakes can occur. Here are some of the frequent errors and how to avoid them:
- Incorrect Number of Sides:
Ensure you count the number of sides correctly. The perimeter formula for a regular polygon is \( P = n \times s \), where \( n \) is the number of sides and \( s \) is the length of each side. Miscounting the sides will lead to incorrect calculations.
- Using Incorrect Side Length:
Verify that the side length used is accurate and consistent for all sides. Since regular polygons have equal side lengths, using different values will result in an incorrect perimeter.
- Unit Conversion Errors:
Always ensure that the side lengths are in the same units before multiplying. If the side lengths are given in different units (e.g., meters and centimeters), convert them to a common unit before calculation.
- Confusion with Irregular Polygons:
Distinguish between regular and irregular polygons. The perimeter of an irregular polygon is the sum of all its side lengths, while the perimeter of a regular polygon is calculated using the formula \( P = n \times s \).
- Calculation Errors:
Double-check your arithmetic calculations to avoid simple mistakes. Using a calculator can help reduce errors.
Example of Common Mistakes
Let's look at an example to illustrate these common mistakes and how to avoid them:
Problem: Calculate the perimeter of a regular hexagon (6 sides) with each side measuring 5 cm.
- Incorrect Approach:
Incorrectly counting the number of sides (e.g., using 5 sides instead of 6).
Incorrect calculation: \( P = 5 \times 5 = 25 \) cm.
- Correct Approach:
Correctly counting the number of sides and ensuring the side length is accurate.
Correct calculation: \( P = 6 \times 5 = 30 \) cm.
How to Avoid These Mistakes
To avoid these mistakes, follow these steps:
- Double-check the number of sides of the polygon.
- Verify the length of each side and ensure all sides are equal for a regular polygon.
- Convert all side lengths to the same unit before performing calculations.
- Use a calculator to minimize arithmetic errors.
- Review your final calculations to ensure accuracy.
Practice Problems
Here are several practice problems to help you master finding the perimeter of regular polygons. Work through each problem step by step, ensuring you understand the process.
-
Problem 1: Find the perimeter of a regular hexagon with each side measuring 7 units.
Solution:
- Number of sides (\( n \)) = 6
- Length of each side (\( s \)) = 7 units
- Perimeter (\( P \)) = \( n \times s = 6 \times 7 = 42 \) units
-
Problem 2: Calculate the perimeter of a regular pentagon where each side is 5.5 cm long.
Solution:
- Number of sides (\( n \)) = 5
- Length of each side (\( s \)) = 5.5 cm
- Perimeter (\( P \)) = \( n \times s = 5 \times 5.5 = 27.5 \) cm
-
Problem 3: A regular octagon has a side length of 3 meters. Determine its perimeter.
Solution:
- Number of sides (\( n \)) = 8
- Length of each side (\( s \)) = 3 meters
- Perimeter (\( P \)) = \( n \times s = 8 \times 3 = 24 \) meters
-
Problem 4: If the perimeter of a regular nonagon (9-sided polygon) is 45 feet, find the length of each side.
Solution:
- Number of sides (\( n \)) = 9
- Perimeter (\( P \)) = 45 feet
- Length of each side (\( s \)) = \( \frac{P}{n} = \frac{45}{9} = 5 \) feet
-
Problem 5: A regular decagon has a perimeter of 70 inches. What is the length of one side?
Solution:
- Number of sides (\( n \)) = 10
- Perimeter (\( P \)) = 70 inches
- Length of each side (\( s \)) = \( \frac{P}{n} = \frac{70}{10} = 7 \) inches
-
Problem 6: Find the perimeter of a regular polygon with 12 sides, each measuring 2.5 centimeters.
Solution:
- Number of sides (\( n \)) = 12
- Length of each side (\( s \)) = 2.5 cm
- Perimeter (\( P \)) = \( n \times s = 12 \times 2.5 = 30 \) cm
These problems will help reinforce your understanding of how to calculate the perimeter of regular polygons. Practice regularly to improve your proficiency.

Advanced Topics
In this section, we delve into more complex and interesting aspects of regular polygons and their perimeters. These topics extend beyond basic perimeter calculations and explore deeper mathematical concepts and applications.
1. Perimeter in Higher Dimensions
While the concept of perimeter applies to two-dimensional polygons, it can be extended to higher dimensions. For example, in three-dimensional shapes, we consider the edge length instead of the perimeter.
2. Perimeter and Circumradius
For regular polygons, the relationship between the perimeter and the circumradius (the radius of the circumscribed circle) can be expressed as:
\[ P = 2nR \sin\left(\frac{\pi}{n}\right) \]
where \( n \) is the number of sides, and \( R \) is the circumradius. This formula is useful in various geometric and engineering applications.
3. Perimeter and Inradius
The inradius (radius of the inscribed circle) is another significant measure. The perimeter can also be related to the inradius:
\[ P = 2nR \tan\left(\frac{\pi}{n}\right) \]
where \( r \) is the inradius. This relationship is especially useful in fields like tiling and material sciences.
4. Perimeter of Star Polygons
Star polygons, such as pentagrams, are interesting regular polygons with complex perimeter calculations. The perimeter of a star polygon is calculated by considering the lengths of the intersecting edges.
\[ P = 2nR \sin\left(\frac{\pi}{n}\right) \]
where \( n \) is the number of vertices, and \( R \) is the circumradius.
5. Perimeter in Complex Polygons
For irregular polygons or polygons with a large number of sides, numerical methods and algorithms are often used to approximate the perimeter. Techniques like the Monte Carlo method can be applied for such approximations.
6. Perimeter in Non-Euclidean Geometry
In non-Euclidean geometries, such as spherical or hyperbolic geometry, the concepts of perimeter and area differ significantly from Euclidean geometry. For example, the perimeter of a polygon on a spherical surface is dependent on the spherical excess, a measure of the deviation from flat geometry.
7. Applications in Real Life
Understanding the advanced concepts of perimeter has practical applications in various fields such as computer graphics, architecture, and physics. For instance, in computer graphics, the perimeter of polygons is used in rendering and collision detection algorithms. In architecture, precise perimeter calculations are crucial for material estimation and structural integrity assessments.
8. Algorithmic Approaches
Advanced algorithms, such as the Graham scan and Jarvis march, are used to compute the convex hull and subsequently the perimeter of complex shapes. These algorithms are fundamental in computational geometry and have applications in robotics, geographic information systems (GIS), and more.
Hướng dẫn cách tính chu vi các đa giác một cách chi tiết và dễ hiểu. Video phù hợp cho những ai muốn học cách tính chu vi của các đa giác đều.
Làm thế nào để: tính chu vi các đa giác
READ MORE:
Hướng dẫn chi tiết cách tìm chu vi của một đa giác đều. Video này phù hợp cho những ai muốn học cách tính chu vi đa giác đều một cách dễ hiểu và nhanh chóng.
Tìm chu vi của một đa giác đều