What is the Square Root of 250? Discover the Answer and More!

The square root of 250 can be determined using different methods, and it is an irrational number as 250 is not a perfect square. Below, we discuss the square root of 250 in detail using various approaches.

Exact and Decimal Form

• Exact Form: \( \pm 5\sqrt{10} \)
• Decimal Form: \( \pm 15.8113883 \) (approx.)

Methods to Find the Square Root of 250

Prime Factorization Method

To find the square root of 250 using prime factorization:

1. Prime factorize 250: \( 250 = 2 \times 5^2 \times 5 \).
2. Group the prime factors into pairs: \( \sqrt{250} = \sqrt{2 \times 5 \times 5 \times 5} = 5 \sqrt{10} \).

Long Division Method

The long division method involves dividing the number in steps to find the approximate square root. This method provides a decimal value of the square root.

Newton's Method

Newton’s formula for finding the approximate square root is:

\[ \sqrt{N} \approx \frac{1}{2} \left( \frac{N}{A} + A \right) \]

where \( N \) is the number (250) and \( A \) is an approximation (e.g., 15.81).

Simplification

To simplify the square root of 250:

\[ \sqrt{250} = \sqrt{25 \times 10} = 5\sqrt{10} \]

Examples

Example 1: Comparing Square Roots

Is the square root of 250 equal to 10 times the square root of 25?

Solution:

\[ \sqrt{250} = 5\sqrt{10} \]

\[ 10 \times \sqrt{25} = 10 \times 5 = 50 \]

Therefore, \( \sqrt{250} \) is not equal to 10 times the square root of 25.

Example 2: Finding Side Length of a Square Rug

James wants to buy a square rug with an area of 250 sq feet. What is the length of each side?

Solution:

\[ \text{Area} = 250 \text{ sq feet} \]

\[ \text{Side length} = \sqrt{250} = 15.81 \text{ feet} \]

Thus, the length of each side of the rug is approximately 15.81 feet.

Understanding the square root of 250 involves exploring various mathematical methods and concepts. The square root of a number is a value that, when multiplied by itself, gives the original number. In the case of 250, this value is approximately 15.81, indicating that 250 is not a perfect square. Below, we will discuss different approaches to finding the square root of 250.

• Using a Calculator: The simplest method is to use a calculator. Enter 250 and press the square root button to get approximately 15.81.
• Prime Factorization: Break down 250 into its prime factors (2, 5, 5, and 5). Pair the factors and simplify to get the square root in radical form as 5√10.
• Newton’s Method: Use the formula √N ≈ ½ (N/A + A) with N=250 and an approximate value of A to iteratively find a close approximation.
• Long Division Method: This involves pairing the digits, finding the largest square less than each segment, and systematically calculating to achieve a precise value.

Each of these methods provides a different perspective on calculating square roots, helping to enhance our understanding of fundamental mathematical principles.

The square root of 250 can be represented both in decimal and radical forms. Understanding these forms helps in different mathematical applications and simplifications.

Radical Form:

The radical form of the square root of 250 is expressed as:

$$ \sqrt{250} $$

By simplifying, we find:

$$ \sqrt{250} = \sqrt{25 \times 10} = \sqrt{25} \times \sqrt{10} = 5\sqrt{10} $$

So, the simplified radical form is:

$$ 5\sqrt{10} $$

Decimal Form:

Using a calculator, the square root of 250 in decimal form is approximately:

$$ \sqrt{250} \approx 15.8114 $$

For practical purposes, this value can be rounded to various decimal places:

• 10th: $$ \approx 15.8 $$
• 100th: $$ \approx 15.81 $$
• 1000th: $$ \approx 15.811 $$

Knowing both forms is beneficial for different mathematical problems, whether you need a precise value or a simplified radical form.

There are several methods to find the square root of 250, each offering a different approach and level of precision. Below are detailed explanations of three commonly used methods: Prime Factorization, Newton's Approximation Formula, and the Long Division Method.

Prime Factorization Method

The Prime Factorization method involves breaking down the number into its prime factors and simplifying under the radical sign.

• Step 1: Factorize 250 into prime numbers: \(250 = 2 \times 5^3\).
• Step 2: Pair the prime factors: \(5^2\) is paired, and 2 and 5 remain under the radical.
• Step 3: Simplify: \(\sqrt{250} = \sqrt{2 \times 5^2 \times 5} = 5\sqrt{10}\).

Newton's Approximation Formula

Newton's method provides an iterative approach to approximate the square root of a number. It is also known as the Newton-Raphson method.

• Step 1: Choose an initial guess. For \(\sqrt{250}\), a good starting point is \(A = 15\) because \(15^2 = 225\).
• Step 2: Apply Newton's formula: \(\sqrt{N} \approx \frac{1}{2} \left( \frac{N}{A} + A \right)\).
• Step 3: Substitute \(N = 250\) and \(A = 15\): \(\sqrt{250} \approx \frac{1}{2} \left( \frac{250}{15} + 15 \right)\).
• Step 4: Calculate: \(\sqrt{250} \approx \frac{1}{2} \left( 16.6667 + 15 \right) = 15.8333\).
• Step 5: Repeat with the new estimate to improve accuracy.

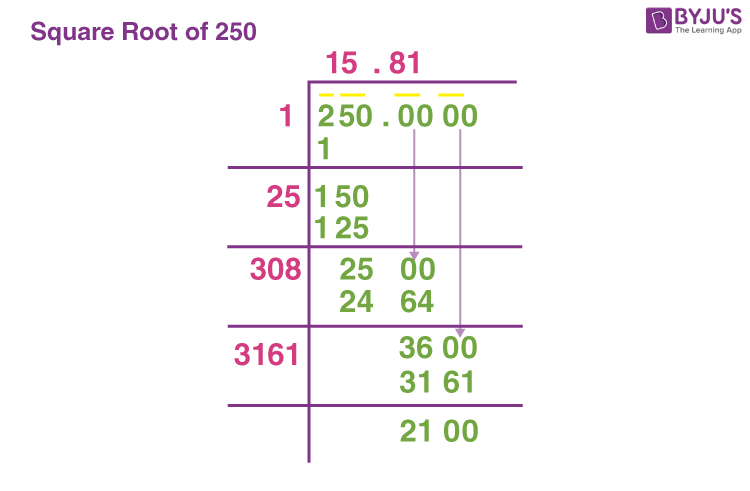
Long Division Method

The Long Division method is a systematic way to find the square root by breaking it down into manageable steps. This method is more precise for non-perfect squares.

• Step 1: Write 250 as a dividend and pair the digits from right to left: \( |2|50| \).
• Step 2: Find the largest number whose square is less than or equal to the first pair (2). In this case, 1 (\(1^2 = 1\)).
• Step 3: Subtract and bring down the next pair of digits: \(2 - 1 = 1\), bring down 50 to get 150.
• Step 4: Double the divisor (1) to get 2. Determine the largest digit \(x\) such that \(20x \times x \leq 150\). Here, \(x = 7\) (\(207 \times 7 = 1449\)).
• Step 5: Subtract and bring down the next pair of zeros to continue with more decimal places if needed.

By following these steps, we can determine that \(\sqrt{250} \approx 15.8114\).

Summary

Each method provides a unique way to understand and calculate the square root of 250. Prime Factorization gives the exact radical form, Newton's Method offers a quick approximation, and the Long Division method delivers a step-by-step precision approach.

Newton's Approximation Formula, also known as the Newton-Raphson method, is an iterative technique to approximate the square root of a number. This method is particularly useful for finding square roots when dealing with non-perfect squares like 250. Here’s a step-by-step guide on how to apply this method to approximate the square root of 250:

1. Choose an Initial Guess: Start with a reasonable initial approximation \( A \). For \(\sqrt{250}\), a good initial guess is \( A = 15 \), since \( 15^2 = 225 \), which is close to 250.

2. Apply Newton’s Formula: Use the formula for Newton's method:

   \[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{N}{x_n} \right) \]

   Where \( x_n \) is the current approximation, and \( N \) is the number whose square root we are finding (in this case, 250).

   • Substitute \( x_0 = 15 \) and \( N = 250 \) into the formula:
   • \[ x_1 = \frac{1}{2} \left( 15 + \frac{250}{15} \right) = \frac{1}{2} \left( 15 + 16.6667 \right) = 15.8333 \]

3. Iterate to Improve Accuracy: Repeat the process using the new approximation \( x_1 = 15.8333 \) to get a more accurate result:

   • Substitute \( x_1 = 15.8333 \) into the formula:
   • \[ x_2 = \frac{1}{2} \left( 15.8333 + \frac{250}{15.8333} \right) = \frac{1}{2} \left( 15.8333 + 15.7895 \right) = 15.8114 \]
   • With each iteration, the approximation gets closer to the actual value of \(\sqrt{250}\).

4. Convergence: Continue iterating until the difference between consecutive approximations is very small. After a few iterations, you will find that:

   • \[ x_3 = \frac{1}{2} \left( 15.8114 + \frac{250}{15.8114} \right) = 15.8114 \]
   • This indicates that the approximation has converged to the square root of 250 with sufficient accuracy.

Newton’s method is highly efficient for finding square roots and provides a good approximation after just a few iterations. For \(\sqrt{250}\), it converges quickly to approximately \( 15.8114 \), making it a valuable tool for calculations where high precision is required.

The square root of 250, like other square roots, has significant applications in various fields of science, engineering, and mathematics. Understanding and calculating the square root of numbers like 250 is crucial for several practical and theoretical reasons. Here’s how the square root of 250 plays a vital role in different areas:

1. Engineering and Design: In engineering, precise calculations are essential. The square root of 250 is used in designing components and structures where diagonal measurements or geometric properties are involved.

   • For example, in civil engineering, calculating the diagonal of rectangular structures or beams requires the use of square roots.
   • In electrical engineering, the square root is used in calculating impedance in AC circuits, where the values involve squared terms.

2. Physics: In physics, the square root of 250 can appear in various formulas and calculations.

   • For instance, it may be used in kinematics to determine the magnitude of a vector in space when its components are squared and summed.
   • It’s also important in quantum mechanics and wave functions, where root calculations are integral to solving equations.

3. Mathematics: Square roots are fundamental in mathematical theories and problem-solving.

   • They are used in solving quadratic equations, where the solutions often require finding the square root of a number.
   • Understanding the properties of square roots helps in simplifying algebraic expressions and in calculating distances in coordinate geometry using the Pythagorean theorem.

4. Statistics: In statistics, the square root function is used to compute standard deviations and variances, which are crucial in understanding the dispersion and variability of data sets.

   • For example, if a data set involves squared deviations from the mean, the square root of the variance gives the standard deviation, a key measure of data spread.

5. Everyday Use: Square roots are also important in everyday life and various practical applications.

   • They are used in financial calculations, such as determining interest rates over time and calculating investment growth, where the time value of money may involve exponential growth and decay requiring square root solutions.
   • Square roots are also involved in measuring areas and distances, such as finding the side length of a square plot of land given its area.

Overall, the square root of 250, while seemingly a simple mathematical concept, is embedded in numerous real-world applications. Its calculation helps in accurate measurements, efficient designs, and deeper understanding in various scientific disciplines. Mastery of square root calculations enriches problem-solving skills and aids in the comprehension of more complex mathematical and scientific phenomena.

The exploration of the square root of 250 reveals not just a numerical value but a gateway to understanding deeper mathematical concepts and practical applications. Throughout this guide, we have examined various methods to approximate and calculate the square root of 250, including:

• Decimal and Radical Forms: We observed that the square root of 250 can be expressed as approximately ±15.8114 in decimal form and ±5√10 in radical form. These forms are essential for different mathematical applications and problem-solving scenarios.
• Prime Factorization Method: By breaking down 250 into its prime factors, we simplified the square root to 5√10, demonstrating how prime factorization helps in understanding the structure of numbers.
• Newton’s Approximation Formula: Using this iterative technique, we achieved a quick and accurate approximation of the square root of 250. Newton’s method is highly valuable for its efficiency and precision in computing roots.
• Long Division Method: This traditional approach provided a step-by-step process to find the square root of 250 with high accuracy, reinforcing fundamental arithmetic skills and the importance of systematic calculation.

Additionally, we explored the Applications and Importance of the square root of 250 across various fields such as engineering, physics, mathematics, and everyday life. Understanding and calculating square roots is crucial for solving complex problems, designing precise structures, analyzing data, and making informed decisions in numerous scientific and practical contexts.

In conclusion, the square root of 250, whether approached through advanced formulas or elementary methods, embodies the elegance and utility of mathematical principles. Mastery of such concepts not only enhances our problem-solving abilities but also deepens our appreciation of the mathematical world. By learning to calculate and apply square roots effectively, we equip ourselves with powerful tools to tackle a wide array of challenges, both theoretical and real-world.