Topic 3 square root of 7: Discover the fascinating world of mathematics with our detailed exploration of the expression "3 square root of 7." This article provides clear explanations, practical examples, and useful tools to help you understand and simplify this mathematical concept. Perfect for students, educators, and math enthusiasts alike.
Table of Content
- Simplifying and Understanding 3 √7
- Introduction to Square Roots
- Understanding the Square Root of 7
- Mathematical Methods for Finding Square Roots
- Babylonian Method and Newton's Method
- Geometric Representation of the Square Root of 7
- Applications in Geometry
- Simplification of Square Roots
- Square Root Calculators and Tools
- Practical Uses of the Square Root of 7
- Conclusion
- YOUTUBE: Khám phá căn bậc hai của 7 và ứng dụng trong toán học, kỹ thuật, và nhiều lĩnh vực khác. Video hấp dẫn giúp bạn hiểu rõ hơn về số học và ứng dụng của căn bậc hai của 7.
Simplifying and Understanding 3 √7
The expression 3 √7 can be simplified and understood using various mathematical concepts. Below are detailed steps and explanations:
Simplification Steps
-
Exact Form: The expression
3 √7remains in its simplified exact form as there are no further simplifications possible without a decimal approximation. -
Decimal Form: To convert
3 √7into a decimal form, first calculate the square root of 7, which is approximately2.64575. Then, multiply by 3:\[
3 \times \sqrt{7} \approx 3 \times 2.64575 = 7.93725
\]
Conceptual Explanation
The principal square root of a number \( a \) is denoted by \( \sqrt{a} \) and is the positive number that, when squared, equals \( a \). In our case, \( \sqrt{7} \) is the number that, when multiplied by itself, gives 7. Therefore, the expression 3 √7 means 3 times the principal square root of 7.
Mathematical Context
Square roots are a fundamental concept in mathematics, especially in algebra and geometry. They are used to solve quadratic equations, understand geometric properties, and in various areas of calculus and higher mathematics.
Additional Examples
-
The square root of 9 is 3, because \( 3 \times 3 = 9 \).
-
The square root of 25 is 5, because \( 5 \times 5 = 25 \).
-
The square root of 49 is 7, because \( 7 \times 7 = 49 \).
Useful Calculators
To explore more about square roots and perform various calculations, you can use the following online calculators:
These tools can help you understand the concept better and simplify various mathematical expressions involving square roots.

READ MORE:
Introduction to Square Roots
Square roots are fundamental concepts in mathematics that represent one of the two equal factors of a number. For any nonnegative number \( a \), the principal square root is denoted by \( \sqrt{a} \). This operation helps in simplifying expressions and solving equations, especially in algebra and geometry.
To simplify a square root, we look for perfect square factors of the number under the radical. For example, to simplify \( \sqrt{45} \), we recognize that 45 can be factored into 9 and 5, where 9 is a perfect square. This allows us to write:
\[ \sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5} \]
This method can be generalized for any number, making it easier to handle complex expressions involving square roots.
For example, the expression \( 3\sqrt{7} \) cannot be simplified further because 7 is a prime number and does not have any perfect square factors. Thus, it remains in its simplest form.
- \( \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3} \)
- \( \sqrt{27} = \sqrt{9 \times 3} = \sqrt{9} \times \sqrt{3} = 3\sqrt{3} \)
- \( \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \)
Understanding and applying these principles allows for efficient problem-solving and a deeper comprehension of mathematical relationships.
Understanding the Square Root of 7
The square root of 7, denoted as \( \sqrt{7} \), is an irrational number approximately equal to 2.64575. Understanding square roots involves various mathematical concepts and methods. Let's explore the different approaches and properties of square roots, specifically focusing on the square root of 7.
- Definition: The square root of a number \( a \) is a value \( x \) such that \( x^2 = a \). For 7, \( \sqrt{7} \) is the number that, when multiplied by itself, gives 7.
- Calculation Methods:
- Trial and Error: This method involves guessing and checking numbers until the square root is found. For 7, this method can be time-consuming due to its irrational nature.
- Approximation: Using methods like the binomial expansion or calculus can provide more accurate approximations. For instance, using binomial expansion, \( \sqrt{7} \) can be evaluated more precisely.
- Using Calculators: Online tools and calculators can quickly provide the square root of 7. These tools often use iterative methods to improve accuracy.
- Properties:
- \( \sqrt{7} \) is an irrational number, meaning it cannot be expressed as a simple fraction.
- It is important in various fields of science and engineering where precise calculations are necessary.
Understanding and calculating square roots are fundamental skills in mathematics. The square root of 7, while irrational, is a significant number with applications in various scientific and engineering disciplines. Tools like calculators and mathematical methods ensure precise values for practical use.
Mathematical Methods for Finding Square Roots
Finding the square root of a number is a fundamental mathematical operation. There are several methods to find square roots, each with its own advantages. Below, we will explore some of the most common methods in detail.
1. Prime Factorization Method
This method involves breaking down the number into its prime factors and pairing them to find the square root.
- Factorize the number into prime factors.
- Pair the factors.
- Take one number from each pair and multiply them to get the square root.
2. Long Division Method
This is a step-by-step method to find the square root of a number, especially useful for non-perfect squares.
- Write the number in decimal form.
- Find the largest integer whose square is less than or equal to the number.
- Subtract the square of this integer from the number.
- Bring down the next pair of digits and repeat the process.
3. Newton-Raphson Method
An iterative method that approximates the square root of a number.
- Make an initial guess for the square root.
- Use the formula: where x is the guess and n is the number.
- Repeat the process until the desired accuracy is achieved.
4. Estimation and Approximation
This method involves guessing the square root and refining the guess through multiplication and adjustment.
- Estimate the square root based on nearby perfect squares.
- Multiply the guess by itself to check if it’s close to the number.
- Adjust the guess and repeat until a satisfactory result is achieved.
5. Using a Calculator
Most modern calculators have a built-in function to find the square root. Simply enter the number and press the square root button to get the result instantly.
| Method | Steps | Example |
|---|---|---|
| Prime Factorization |
|
√36 = 2 × 3 = 6 |
| Long Division |
|
√7 ≈ 2.645 |
| Newton-Raphson |
|
√7 ≈ 2.645 |
Each method has its own use cases and is suitable for different types of numbers and precision requirements. Whether using prime factorization for perfect squares or the long division method for more complex numbers, understanding these methods is crucial for solving square root problems.
Babylonian Method and Newton's Method
The Babylonian Method and Newton's Method are two classical approaches for finding square roots, both of which are iterative techniques that refine approximations to achieve higher accuracy.
Babylonian Method (also known as Heron's Method):
- Choose an initial guess \( x_0 \) for the square root of a number \( n \).
- Improve the guess using the formula: \[ x_{k+1} = \frac{1}{2} \left( x_k + \frac{n}{x_k} \right) \]
- Repeat the process until the desired accuracy is achieved.
This method is simple and converges quickly for positive numbers. It works by averaging the guess \( x_k \) and the quotient \( \frac{n}{x_k} \), progressively honing in on the square root of \( n \).
Newton's Method (Newton-Raphson Method):
- Start with an initial guess \( x_0 \).
- Apply the iterative formula: \[ x_{k+1} = x_k - \frac{f(x_k)}{f'(x_k)} \] For square roots, where \( f(x) = x^2 - n \), this simplifies to: \[ x_{k+1} = \frac{1}{2} \left( x_k + \frac{n}{x_k} \right) \] which is identical to the Babylonian Method.
- Continue iterations until the change in \( x \) is sufficiently small.
Newton's Method is a powerful and general approach for finding roots of functions, and when applied to square roots, it yields the same updates as the Babylonian method. The convergence is quadratic, meaning it doubles the number of correct digits with each step, making it very efficient.
Both methods are foundational in numerical analysis and are still widely used due to their simplicity and effectiveness. They are applicable not just to square roots but to a broad range of problems in mathematics and engineering.
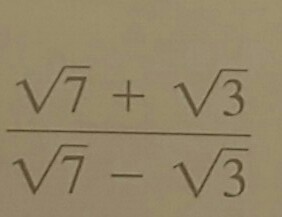
Geometric Representation of the Square Root of 7
Understanding the geometric representation of the square root of 7 helps visualize and comprehend its value beyond mere computation. The square root of 7, approximately equal to 2.645, can be represented geometrically in several ways.
- Number Line Representation:
To represent √7 on a number line, identify two consecutive whole numbers between which √7 lies, namely 2 and 3. By dividing the interval into smaller segments, you can approximate the position of √7 more accurately.
- Square Construction:
Construct a square with an area of 7 square units. The length of each side of this square will be √7 units, which visually demonstrates the value.
- Right-Angled Triangle:
Consider a right-angled triangle where the hypotenuse is √7 units. Using the Pythagorean theorem, you can set the other two sides such that their squares sum up to 7. For instance, one leg could be √3 and the other 2, satisfying the equation (√3)^2 + 2^2 = 7.
These geometric approaches not only help in understanding the value of √7 but also in realizing its applications in different mathematical contexts.
Applications in Geometry
The square root of 7 has several applications in geometry, particularly in problems involving right triangles, distances, and areas. Here, we explore some of these applications:
-
Pythagorean Theorem: In right triangle problems, the square root of 7 can appear as a leg or the hypotenuse. For instance, if one leg is √7 units long and the other leg is 3 units, the hypotenuse can be found using the Pythagorean theorem:
- \( c = \sqrt{(3^2 + (\sqrt{7})^2)} = \sqrt{(9 + 7)} = \sqrt{16} = 4 \)
-
Distance Calculation: When calculating the distance between two points in a coordinate system, the square root of 7 might be used. For example, to find the distance between points (0, 0) and (√7, 3), use:
- \( d = \sqrt{(\sqrt{7} - 0)^2 + (3 - 0)^2} = \sqrt{7 + 9} = \sqrt{16} = 4 \)
-
Geometric Shapes: The square root of 7 can also be applied when working with circles, triangles, and other geometric shapes where certain dimensions or areas involve irrational numbers.
-
Trigonometry: In trigonometry, the square root of 7 might appear in the context of solving for angles or lengths in triangles. For example, if a triangle has a leg of √7 and another leg of 3, you can find the angles using trigonometric ratios.
Understanding these applications helps in solving complex geometric problems and deepens the comprehension of how irrational numbers like the square root of 7 integrate into geometry.
Simplification of Square Roots
The process of simplifying square roots involves expressing the root in its simplest radical form. For example, let's consider the square root of 7.
To simplify a square root:
- Factor the number inside the square root into its prime factors.
- Pair the prime factors and move one factor out of each pair outside the square root.
- If no pairs are present, the square root is already in its simplest form.
For example, the square root of 7 cannot be simplified further as 7 is a prime number. Therefore, √7 is already in its simplest form.
To illustrate the simplification process further, let's look at the simplification of 3√7:
- First, recognize that
3√7is the product of 3 and√7. - Since 7 is a prime number, it cannot be simplified further. Thus,
√7remains as it is. - The term
3√7is already in its simplest form.
In cases where the radicand (the number inside the square root) is not a prime number, further simplification is possible. For instance:
- Consider
√50. - Factor 50 into prime factors:
50 = 2 × 5 × 5. - Pair the prime factors:
5 × 5 = 25. - Move one 5 out of the square root:
√50 = 5√2.
This method applies universally to all square roots, ensuring they are expressed in their simplest form.
| Radicand | Prime Factors | Simplified Form |
|---|---|---|
| 18 | 2 × 3 × 3 | 3√2 |
| 72 | 2 × 2 × 2 × 3 × 3 | 6√2 |
| 45 | 3 × 3 × 5 | 3√5 |
Using these principles, you can simplify any square root to its most basic form.
Square Root Calculators and Tools
Calculating the square root of a number can be simplified with the help of online calculators and tools. These tools not only provide quick results but also explain the steps involved in the calculation. Here are some popular square root calculators and how they can be used:
-
Mathway Square Root Calculator:
Mathway offers a comprehensive square root calculator that allows users to input any radical expression and find its square root. It provides both exact and decimal forms of the result. To use Mathway:
- Enter the radical expression in the input box.
- Click the blue arrow to submit.
- Select "Calculate the Square Root" from the topic selector and view the result.
This tool is especially useful for students and professionals who need step-by-step solutions.
-
Symbolab Square Root Calculator:
Symbolab is another powerful tool that helps in finding the square roots of numbers. It supports a wide range of mathematical functions and provides detailed solutions. To use Symbolab:
- Go to the Symbolab square root calculator page.
- Enter the number or expression for which you need the square root.
- Press "Calculate" to get the result along with a step-by-step explanation.
Symbolab also allows users to explore additional functions like simplifying and solving equations involving square roots.
-
Omni Calculator:
Omni Calculator offers a user-friendly interface for calculating square roots and simplifying them. It explains the process of simplification clearly. To use Omni Calculator:
- Enter the number under the square root symbol.
- Check the factors to see if any are perfect squares.
- The calculator will simplify the square root and provide the result.
Omni Calculator is great for learning how to manually simplify square roots by breaking them down into their factors.
In addition to these tools, high precision calculators like Miniwebtool's Square Root Calculator can provide highly accurate decimal results for square roots. These tools are beneficial for high-level mathematical computations and research purposes.
Using these calculators, you can easily find and understand the square root of any number, including non-perfect squares like the square root of 7. These tools not only give you the final answer but also enhance your understanding of the mathematical concepts involved.

Practical Uses of the Square Root of 7
The square root of 7, an irrational number approximately equal to 2.64575, has various practical applications in different fields. Here are some of the significant uses:
- Engineering and Construction: In engineering, the square root of 7 can be used to calculate dimensions and distances that involve right triangles, applying the Pythagorean theorem where one of the sides might be related to this value. For instance, in civil engineering, ensuring the structural integrity of buildings and bridges often involves calculations where square roots play a crucial role.
- Physics: The square root of 7 appears in formulas related to physical laws. For example, in the context of wave mechanics, the speed of a wave on a string or in a medium can involve square root calculations. Similarly, energy levels in quantum mechanics often require precise computations involving square roots.
- Finance: In financial mathematics, square roots are used in various calculations, such as determining the volatility of an asset's returns. The formula to calculate standard deviation, which measures the amount of variation or dispersion of a set of values, often involves the square root of variances.
- Statistics: In statistical analysis, the square root of 7 can be used when calculating standard deviations and variances. This is important for data analysis, risk assessment, and in determining confidence intervals in hypothesis testing.
- Computer Graphics: In computer graphics and game development, square roots are frequently used in algorithms that compute distances between points in 2D or 3D space. For example, to determine the distance between two points (x1, y1) and (x2, y2), the formula involves the square root of the sum of the squares of the differences in each dimension.
- Geometry: The square root of 7 is also significant in geometric calculations. For instance, it is used to determine the length of the diagonal in rectangular shapes when the sides are in proportion related to this value. This is particularly useful in design and architecture.
- Astronomy: In astronomy, calculations involving distances between celestial objects, such as stars and planets, often use square roots. This can be essential for determining gravitational forces, orbital mechanics, and other critical measurements.
Understanding the square root of 7 and its applications can provide valuable insights across various disciplines, highlighting the interconnectedness of mathematics with real-world problems and solutions.
Conclusion
The square root of 7, approximately 2.6457513110645906, is a fascinating number with various applications in mathematics and beyond. Despite being an irrational number, its presence is felt in numerous practical scenarios, showcasing the beauty and utility of mathematical concepts.
Throughout this guide, we have explored the theoretical foundations, computational methods, and practical uses of the square root of 7. From geometric interpretations to algebraic simplifications, this number demonstrates the interconnectedness of different mathematical disciplines. The approximation methods, such as the Babylonian method and Newton's method, highlight the ingenuity of ancient and modern mathematicians in tackling complex problems.
The applications of the square root of 7 extend beyond pure mathematics. In geometry, it appears in calculations involving right-angled triangles and other shapes, proving essential for accurate measurements and constructions. In various practical contexts, understanding and utilizing the square root of 7 can lead to more efficient problem-solving and deeper insights into the nature of numbers.
As we continue to explore and appreciate the properties of the square root of 7, we are reminded of the ever-evolving nature of mathematics. Each new discovery builds upon the knowledge of the past, offering fresh perspectives and solutions for future challenges. Embracing the complexity and elegance of numbers like the square root of 7 enriches our understanding and appreciation of the mathematical world.
In conclusion, the square root of 7 is not merely a numerical value but a symbol of the vast and intricate landscape of mathematics. Its study enhances our problem-solving skills, fosters a deeper appreciation for mathematical beauty, and encourages us to explore further into the mysteries of numbers.
Khám phá căn bậc hai của 7 và ứng dụng trong toán học, kỹ thuật, và nhiều lĩnh vực khác. Video hấp dẫn giúp bạn hiểu rõ hơn về số học và ứng dụng của căn bậc hai của 7.
Căn bậc hai của 7
READ MORE:
Khám phá cách giải phương trình (Căn bậc hai của 3 + Căn bậc hai của 7)^2 qua video hấp dẫn. Hướng dẫn chi tiết giúp bạn hiểu rõ hơn về các bước giải và ứng dụng trong toán học.
Giải phương trình (Căn bậc hai của 3 + Căn bậc hai của 7)^2